西双版纳隧道爆破开挖动力学特征及损伤效应

王永伟，李冠中

(中交第二航务工程局有限公司 第五工程分公司，武汉 430012)

1 研究背景

随着中国基础建设和 “一带一路”等政策的不断实施，铁路隧道的施工不断增加，长大隧道、软岩深埋隧道等屡见不鲜。隧道的施工开挖方式必将影响隧道围岩的安全稳定性[1-2]，而当隧道穿越高地应力的软岩区域时，如何控制爆破振动对于隧道自身结构以及已有衬砌的扰动损伤至关重要[3-4]，因此研究软岩隧道围岩的稳定性评价具有重要的理论应用价值。

目前国内外研究学者多采用数值模拟、理论分析、工程实测等综合方法对隧道围岩的稳定性进行了不同层次和角度的研究[5-6]。吉凌等[7]采用有限元法研究了不同掏槽方式影响下大断面隧道的振动响应，得到的优化掏槽方式对于现场施工进程和施工成本有较好的控制。而围岩级别的降低和地应力的逐渐提高，使得隧道的掏槽方式对于围岩稳定性的影响逐渐降低，而开挖方式和支护技术的选择逐渐成为影响隧道安全稳定的另一关键因素[8]。另一方面，隧道稳定性的评价手段也对隧道开挖方式的优化选择存在重大影响[9]。赵桂林等[10]采用隧道内质点的最大振动速度作为隧道稳定性评价的重要指标，然而针对隧道内质点爆破振动速度作为隧道安全性的评价指标，许多学者又将爆破振动速度分为幅值、频率、波长三方面进行研究，然后基于傅里叶变换原理和应力波基础等理论，建立了能够反映隧道安全稳定性的评价指标。目前这些关于考虑了质点振动速度阈值的评价指标主要有以下3种：①基于希尔伯特-黄变换(Hilbert-Huang)等理论，研究了隧道内监测点处的振动频率与衬砌结构自身频率之间的对应关系，并基于频率建立了相关隧道控制标准[11-12]；②基于应力波理论中的一维弹塑性应力波在一维节理中的传播建立的应力-振速对应关系曲线，并结合岩石屈服准则建立的应力控制标准[13]；③基于规范和标准建立频率、埋深、地形等对应的隧道安全振动速度控制标准[14-15]，建立的隧道安全稳定性控制标准具有考虑振动波的参数特征、简单易用的优点。其中李小贝[16]结合实际工程案例，研究了隧道不同位置处振动速度对于隧道围岩稳定性的影响，但是仅考虑了隧道衬砌表面的安全稳定性，而未考虑距离掌子面更近的围岩内部的损伤情况。杨小林等[17]结合现场实际振动速度峰值在不同爆破振动次数作用下，萨道夫斯基的拟合系数的变化来研究爆破累积损伤对于围岩结构的影响，但其研究手段过于单一，研究隧道近区累积损伤缺少岩体内部声波现场测试的结果，同时其仅采用现场实测数据，未增加数值模拟等手段进行综合研究。李红泽[18]以实际工程案例为背景，对振动速度的压力公式进行修正，但是主要研究了衬砌结构的影响，忽略了掌子面近区围岩的损伤。

本文基于实际工程案例，结合数值模拟和现场实测数据，引入隧道损伤深度概念，研究了隧道不同轴向和环向位置处围岩的振动响应特征，并分析了爆破振动荷载作用下隧道围岩的损伤范围，对围岩爆破振动控制进行研究，为类似工程提供参考。

2 工程背景

本工程位于云南省西双版纳傣族自治州野象谷站—西双版纳站区间，为玉溪至磨憨铁路工程的一部分。左右线间距为4.2～5.083 m。工程北接昆玉铁路的玉溪站，南止于勐腊边境磨憨口岸，止点里程为DK358+730，全长10 680 m。西双版纳隧道采用矿山法施工。隧道建筑界限为14.7 m(宽)×14.3 m(高)，隧道埋深340 m，隧道内路面横坡-1.5%～+1.5%，路面标高24.2～25.8 m。围岩级别为Ⅲ级，采用全断面法施工。采用的爆破参数为：雷管分段为1～17段，共10响；最大一响药量35 kg。炮孔布置如图1所示。

图1 西双版纳隧道炮孔布置Fig.1 Layout of blast holes in a tunnel of Xishuangbanna

模拟条件的参数选取直接影响模拟结果，根据西双版纳隧道工程地质勘察结果，在岩体力学室内试验的基础上，选用作为模拟隧道一般条件下的围岩结构的物理力学参数，如表1所示。

表1 数值模型相关计算参数Table 1 Calculation parameters for numerical model

3 数值模拟

3.1 掏槽孔边缘等效的压力荷载

本文采用三角形荷载垂直施加至数值模型掏槽孔等效弹性边界，也就是炮孔粉碎区边缘，如图2所示，并根据经验公式即式(1)可以计算出应力峰值[19]。

图2 数值模拟爆破三角形荷载Fig.2 Triangle blast load in numerical simulation

(1)

式中：P0为爆轰平均压力；ρ0为炸药密度,ρ0=1 200 kg/m3；D为爆轰速度,D=4 100 m/s；γ为等熵指数[20]，γ=3；dc为药卷直径，dc=32 mm；db为炮孔直径，db=42 mm。等效到炮孔粉碎区边缘的爆炸荷载Pbe为[19]

(2)

式中：k与掏槽的个数以及爆破的参数有关[20]，k=10；rb为炮孔半径；rc为粉碎区半径；rf为破裂区半径，参考文献[21-22]可知，rc=3rb，rf=10rb；μ为岩石泊松比。其中荷载上升时间为1 ms, 正压时间为7 ms[20]。

3.2 数值计算模型

采用动力有限元计算软件ANSYS/LSDYNA，结合实际工程背景和圣维南原理，选择西双版纳隧道轮廓线3～5倍洞径作为数值模型计算的塑性变形边界，故计算模型尺寸为100 m×100 m×90 m (x×y×z)，采用SOLID164单元来划分网格，并选取整体模型除上部自由表面外的所有面为无反射边界。如图3所示。选取现场实测隧道掌子面前方50 m的5个监测点的振动速度峰值与数值模型内得到的振动速度峰值进行分析，测试结果如表2所示，同时图4(a)展示了x、y、z方向振动速度峰值对比, 图4(b)展示了与爆心直线距离为50 m时，1#监测点y方向的振动速度时程曲线现场实测数据与数值模拟数据的对比。

图3 数值模型示意图Fig.3 Schematic diagram of the numerical model

表2 现场实测数据与数值模拟对比Table 2 Comparison between field measured data and numerical simulation

图4 实测与模拟振动速度峰值对比Fig.4 Comparison of peak vibration velocity between measurement and numerical simulation

从图4可以得出数值模拟和现场实测变化趋势相似，且误差相差不大，最大误差率不超过7.14%，故数值模拟所得模型可以用来研究西双版纳隧道爆破开挖动力学特征及损伤效应。

4 隧道横断面动力响应特征

4.1 开挖断面不同位置处质点速度的变化规律

爆破产生的地震波由远及近传播，并且逐渐由体波向面波转化。为了解不同隧道断面处爆破地震波造成的隧道质点的振动变化规律，选取距掌子面距离分别为1、5、30 m处隧道轮廓的质点,其振动速度峰值分布规律如图5所示。

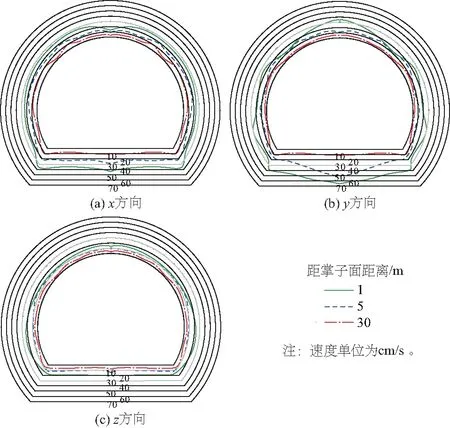
图5 隧道开挖断面振动速度峰值分布Fig.5 Distribution of peak vibration velocity in excavation section of the tunnel

(1)从图5不难看出，在隧道爆破近区，隧道内质点的垂直方向振动速度峰值大于隧道径向方向振动速度峰值大于隧道轴向方向振动速度峰值(y方向>x方向>z方向)，说明垂直方向的振动在距离掌子面较近区域为主要振动传播方向。其原因为隧道埋深较大，隧道围岩级别较好，随着V形掏槽区的起爆，隧道爆破产生的地震波主要包括体波和面波，隧道轴向和隧道径向均存在自由面，故均存在一定程度衰减，导致隧道垂直方向的振动速度峰值较大。同时随着距离掌子面距离的增加，隧道内质点的振动传播速度逐渐减小，而且y方向衰减最为严重，x方向次之，z方向最小，说明随着与隧道掌子面距离的增加，隧道内质点速度衰减主要以y方向为主。

(2)从图5(a)隧道内质点x方向的传播规律不难看出,隧道顶部和隧道的拱肩处，围岩振动速度较小，而在隧道的拱脚和底板处，振动速度较大。这是由于隧道为椭圆形结构，在隧道的拱脚处容易发生应力集中而导致此处的应力过大，根据应力波理论，隧道拱脚处的应力较大，从而导致此处的波阻抗较大，故而此处的振动速度峰值较大，同时由于底板在高地应力的情况下，爆破开挖导致隧道整体应力重新分布而出现卸荷回弹的情况，导致此处应力波的传播被一定程度放大，故此处围岩质点振动速度较大。

(3)从图5(b)隧道质点垂直方向的传播规律不难看出,隧道底板和隧道边墙的振动速度较大，而隧道顶部的振动速度次之，隧道拱肩和拱脚处振动速度最小。说明在隧道垂直方向，隧道掏槽区的开挖导致隧道内出现临空面，为隧道的进一步变形提供了条件，同时隧道内垂直方向的振动对应于隧道爆破地震波中的横波，也就是SH波和SV波，而横波在自由面和岩体分界面极易进行反射和折射，故导致在隧道爆破近区隧道顶部和边墙以及底板处垂直方向振动速度较大，拱脚和拱肩处存在应力集中现象和特殊的部位结构，而导致应力波引起的振动速度较小。

4.2 隧道轴向不同位置处质点峰值合速度的变化规律

隧道掌子面爆破产生的地震波对于隧道围岩及衬砌的影响表现为引起隧道质点变形和振动，利用验证后的数值模型研究在隧道轴向方向上不同位置处质点的合振动速度变化规律，如图6所示。

图6 隧道轴向方向上不同位置处质点的合振动速度分布Fig.6 Distribution of the joint vibration velocity at different distances from blast face in axial direction of the tunnel

(1)从图6不难看出隧道轮廓不同位置处的合振动速度的峰值在隧道底板处最大，拱脚处次之，拱肩处再次之，边墙和拱顶最小。说明隧道爆破开挖过程中，高地应力的情况下，隧道开挖卸荷回弹导致隧道底板处振动速度最大。

(2)从图6可以看出，隧道合振动速度峰值未出现在隧道掌子面的正上方，而出现在隧道未开挖区，说明隧道爆破过程中掏槽孔中下部的位置引起的爆破振动速度最大，同时隧道未开挖区的质点振动速度衰减较隧道已开挖区衰减较慢，说明隧道未开挖区不存在自由表面而导致质点振动速度衰减较慢。

4.3 爆破损伤效应研究

为了进一步研究岩体深部不同位置处的损伤效应，现场结合声波测试系统，对距隧道掌子面不同位置处的岩体损伤规律进行研究，故选取距离掌子面分别为10、20、40、80 m处不同靠近拱脚位置处进行研究分析，在爆破次数分别为0、1、3、5、10次后分别进行3次测量，并取平均值。根据爆破前后声波速度降低的原理，将隧道的位移损伤深度进行确定，测点布置如图7所示，其中由于设备自身原因，声波检测操作过程中每次移动范围为0.5 m；隧道距掌子面不同位置处每次爆破前后声波测试结果如图8所示。其中《水工建筑物岩石基础开挖工程技术规范》(SL47—94)中有如下规定：

图7 测点布置示意图Fig.7 Arrangement of measurement points

(3)

式中：D为岩体损伤度；K为岩体完整性系数；η为声速降低率；E0为爆破前岩体的弹性模量；E为爆破后岩体的等效弹性模量；v0为爆破前岩体的声波速度；v为爆破后岩体的声波速度。并且定义岩体受到爆破损伤时，对应的岩体损伤度阈值为0.19。根据图8中测试结果数据，定义岩体爆破前岩体的声波速度为5.6 km/s；并统计爆破次数与损伤深度关系如表5所示。

图8 声波速度-孔深曲线Fig.8 Curves of acoustic velocity versus hole depth

表5 爆破次数与围岩损伤深度关系Table 5 Relationship between the number of blasting and the depth of damage to surrounding rock

(1)由图8不难看出，随着与掌子面水平距离的逐渐增加，岩体内围岩的声波速度逐渐降低，并且随着爆破次数的增加，声波速度呈逐渐衰减的变化趋势，并且在一定程度后趋于稳定。

(2)随着距隧道自由面轴向距离的增加，声波在围岩体内的传播速度逐渐增大，说明爆破振动对于围岩的损伤存在一定的范围限制，同时在隧道掌子面不同距离处，隧道深部围岩的声波速度与探测孔口直线距离之间的变化趋势呈指数型变化规律，并且在距离隧道自由面2 m范围内，声波速度降低较小，而且根据式(3)可知，声波速度越小，隧道围岩损伤越严重，故距离隧道自由面2 m范围内损伤较严重。

(3)通过爆破次数和围岩损伤深度关系可以看出，随着与隧道掌子面水平距离的增加，围岩的损伤深度逐渐减小，并且在爆破次数较少时变化不大，但是随着爆破次数的增加，两者差值逐渐增加，如当爆破次数为1次时，不同距离处的损伤深度分别为2.0 m和2.5 m，而当爆破次数为10次时，围岩的损伤深度从2.0 m增加至4.0 m,说明反复多次爆破振动对于隧道围岩的完整性存在影响，但是影响范围有限。

5 结 论

(1)在隧道爆破近区，隧道内质点的垂直方向振动速度峰值大于隧道径向方向振动速度峰值大于隧道轴向方向振动速度峰值，同时随着距离掌子面距离的增加，隧道内质点的振动传播速度逐渐减小，而且y方向衰减最为严重，而x方向次之，z方向最小。隧道内质点x方向的振动速度在隧道顶部和拱肩处较小，而在隧道的拱脚和底板处较大。在隧道内质点垂直方向，隧道底板和隧道边墙的振动速度较大，而隧道顶部的振动速度次之，隧道拱肩和拱脚处最小。

(2)隧道合振动速度峰值未出现在隧道掌子面的正上方，而出现在隧道未开挖区，同时隧道未开挖区的质点振动速度衰减与隧道已开挖区衰减相比较慢。

(3)随着距隧道自由面轴向距离的增加，声波在围岩体内的传播速度逐渐增大，同时随着与掌子面水平距离的逐渐增加，岩体内围岩的声波速度逐渐降低，并且随着爆破次数的增加，声波速度呈逐渐衰减的变化趋势，但在一定次数后趋于稳定，说明爆破振动对于围岩有一定的损伤，但损伤范围有限。