关于无穷小的若干比较方法及应用

绪玉珍

(江苏师范大学科文学院 221000)

极限理论是高等数学的基础，函数的极限是极限理论的一个重要组成部分.极限为零的变量称为无穷小量，简称“无穷小”，在函数及数列的极限、函数的连续性、微分和积分的定义中都有无穷小的应用.然而，理解清楚无穷小的概念以及运算有一定的难度.无穷小的比较问题，不仅是高等数学的重要内容，也是历年全国硕士研究生招生考试的重要考点.本文主要针对无穷小的比较给出了几种方法，有利于读者进一步理解无穷小的含义以及更加系统地掌握此类问题的解决方法.

1根据定义比较无穷小

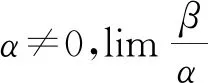
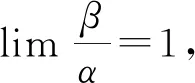
例1 当x→0时，比较2x-x2与x2-2x3的阶.

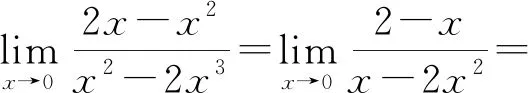
所以2x-x2是比x2-2x3低阶的无穷小.

注1 不是任意两个无穷小都可以比较，因为只有当两个无穷小量比值的极限存在或为无穷大时，才可以比较这两个无穷小.特别地，xk+ο(xk)是x的k阶无穷小(k>0).类似于这个方法，对于无穷小的比较，除了可以使用定义，还可以通过确定每个无穷小的阶，然后比较阶的大小来比较两个无穷小.

2 比较无穷小的阶

2.1 等价无穷小定阶法

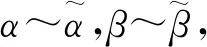
定理1只适用于函数相乘或者相除形式的极限，加减法并不适用.

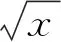
2.2 与(x-a)k(k>0)比较定阶法

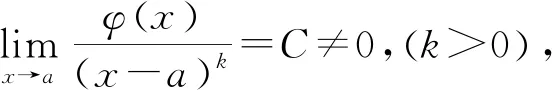
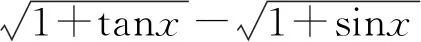
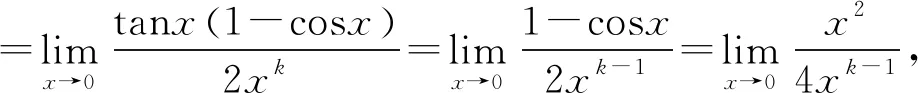
2.3 泰勒公式定阶法

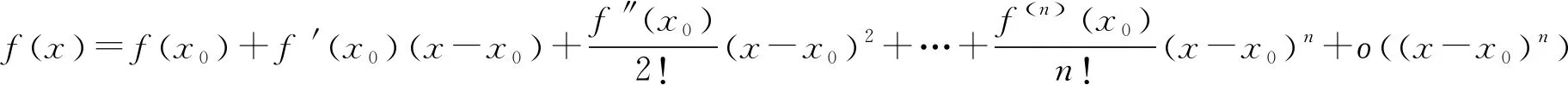
取x0=0，那么有带有佩亚诺余项的麦克劳林公式：

对于一些常见函数相加减的形式，用不了等价无穷小替换时，泰勒公式是个很好的选择.

例4 当x→0时，ex-(ax2+bx+1)是比x2高阶的无穷小，求a,b.

泰勒公式在求极限时使用方便，实际上利用泰勒公式还可以找一个无穷小量的等价无穷小.

特别地，若f(x0)=0，f′(x0)≠0，则当x→x0时，f(x)～f′(x0)(x-x0).

注2 在利用泰勒公式求函数相加减后的量的等价无穷小时，要将各函数展开到相同阶数，并且在加减运算完成后至少要剩余一个非零项，才可以根据推论1得到函数的等价无穷小.

2.4 求导定阶法

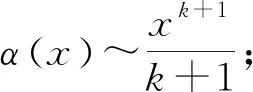
此定理由洛必达法则容易证明.

由定理3可知，比较两个无穷小α与β的阶，可以转化为比较它们各自的导函数α′与β′的阶数，α′与β′阶数具有什么样的关系，则α与β阶数具有同样的关系.当前面三种定阶法都不能很好地处理无穷小比较的问题时，求导定阶法往往可以解决一定的问题.特别地，如果遇到多个无穷小是积分上限的函数，在比较这些无穷小时，求导定阶法可以快速地解决问题.

例5 (2020年全国硕士研究生招生考试试题)当x→0+时，下列无穷小量中阶数最高的是( ).

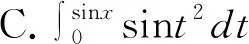
解当x→0+时，由于四个选项中的无穷小都是积分上限的函数，比较它们的阶数，相当于比较它们各自的导函数的阶数.

将以上四种确定无穷小的阶数的方法灵活使用，可以更加有效地处理无穷小的比较问题.

4结论

本文主要从无穷小比较的定义、等价无穷小定阶法、比较定阶法、泰勒公式定阶法、求导定阶法五种方法系统地归纳了无穷小量的比较问题，并结合实例给出了分析过程，使方法可以很好地结合实例进行应用.灵活使用这些方法，可以做到更加有效地解决无穷小的比较问题.