基于响应面法对自攻螺钉连接强度的研究＊

吴艳云 穆天驰 张东民 周伟民 舒恬田

（①上海应用技术大学机械工程学院，上海 201418；②上海东风汽车专用件有限公司，上海 201419）

自攻螺钉广泛应用于汽车制造行业中，特别是新能源汽车零部件和底盘的连接，由于工作环境复杂，要求具备较高的连接强度、使用寿命长、耐磨损和耐腐蚀。传统的热熔工艺流程复杂，需要开底孔，工作效率低，连接强度不够，连接板件间内壁易开裂，切屑较多，螺纹孔成型质量差，针对大批量生产的零部件采用无屑快速冷挤压成形工艺[1]。自攻螺钉钉头锥形截面是影响螺纹孔无屑冷挤压成形的关键，同时通过响应面法针对多组试验参数进行优化，获得最优参数组合。

近年来，通过响应面法分析锻压成形零部件工艺参数的方法成为解决产品缺陷的有效方法。李奇涵等[2]通过响应面法研究特殊材料下高强钢热冲压成形参数的优化方案，有效减小了起皱倾向区域的面积。谈顺强等[3]基于响应面法研究铝制发动机罩的冲压工艺，有效控制了产品的最大减薄率和最大回弹量。侯红玲等[4]通过对内螺纹冷挤压工艺的研究大幅降低了内螺纹成形的挤压温度和挤压扭矩，有效提升丝锥寿命。田海洋等[5]基于Deform-3D软件对阀螺钉冷挤压工艺进行数值模拟，得到了能够有效降低挤压成形过程中应力应变的优化工艺参数。Wei W等[6]通过响应面法对模具结构和挤压速度进行优化，得到控制产品缺陷和减少加工余量的优化方案。

本文通过构建数学模型和数值模拟相结合的方法对自攻螺钉冷挤压成形工艺方案进行优化，并通过试验验证螺纹孔成形质量，成形载荷和切屑的分布，有效降低企业开发产品的成本，缩短研发周期，提升产品市场竞争力。

1 有限元模型建立及参数选择

1.1 有限元模型建立

针对冷挤压成形过程中由于成形载荷大，导致工件内壁开裂的情况，现通过SolidWorks软件建立以薄板件为工件和自攻螺钉为模具的三维模型，并按照工件与模具间的位置关系进行装配。整体装配图如图1所示，整体模型由上冲头自攻螺钉、组合凹模、坯料和下冲头4个部分组成，其中自攻螺钉模型如图2所示。

图1 装配模型图

图2 自攻螺钉模型图

将上冲头自攻螺钉、组合凹模、坯料和下冲头4个模型保存为STL格式，导入到Deform-3D软件中进行有限元仿真。设置坯料材料为6063铝合金，定义为塑性体，网格划分为 60 000 个，为了保证仿真结果的精确性，对主要变形区域进行网格细化处理，应变率为 1～100 s-1。设置x、y、z三个方向的边界约束条件，不考虑模具和冲头发生形变，将其设为刚体，模具初始温度为20 ℃，由于工件表面冷挤压成形前要经过特殊的磷化处理，因此摩擦类型选为剪切摩擦。

1.2 工艺缺陷分析

自攻螺钉在冷挤压过程中形成螺纹孔，螺纹孔成形质量直接影响零件间的连接强度，成形过程中残留的切屑过多也会影响螺钉连接效果。而根据初步给定的成形方案：θ=22°，L=10 mm，v=628 r/min，f=0.3。在此参数下进行仿真，分析冷成形时的金属流动规律。螺纹孔冷挤压成形过程中的速度矢量图如图3所示。根据金属成形过程中材料塑性流动最小阻力定理，反挤压成形螺纹孔时，金属向两端阻力较小的方向流动，由于受到上冲头自攻螺钉和模具的限制，坯料下部金属向两侧侧壁流动阻力逐渐增大，成形载荷逐渐增大。随着挤压深度的增加，内壁受到的冲击载荷急剧增加。特别是在冷挤压成形结束阶段，金属流动缓慢，成形阻力急剧增大，应力在螺纹孔底部和内壁集聚极易导致螺纹孔内壁开裂[7]。

图3 金属流动速度矢量图

1.3 工艺参数选择

自攻螺钉冷挤压成形过程中，冲头锥台斜角、锥台高度、挤压速度和冲头与工件间摩擦系数是决定螺纹孔成形质量的关键因素。为了减小自攻螺钉冷挤压过程中的成形载荷，设计响应面法和Deform-3D软件数值模拟相结合的方法，对冷挤压过程中影响成形载荷较大的因素进行优化分析，建立二阶稳态响应模型以获得最优参数组合。不同的冲头锥台斜角和挤压速度影响金属流动规律，进而影响螺纹孔的成形质量和切屑分布情况；冷挤压成形过程中随着切屑的产生，上冲头与坯料间的摩擦增大，导致成形阻力增加，同时模具温度急剧上升进而影响螺纹孔成形质量；冲头锥台斜角θ和冲头锥台高度L都会影响冲头尖端形状，冲头尖端与坯料最先接触，进而产生切屑，不同的冲头形状与坯料和切屑接触面积不同，受周围坯料和切屑的阻力不同。故本次以v、f、θ和L作为试验变量，成形载荷F作为优化目标。设计试验变量的因素水平如 表1所示。

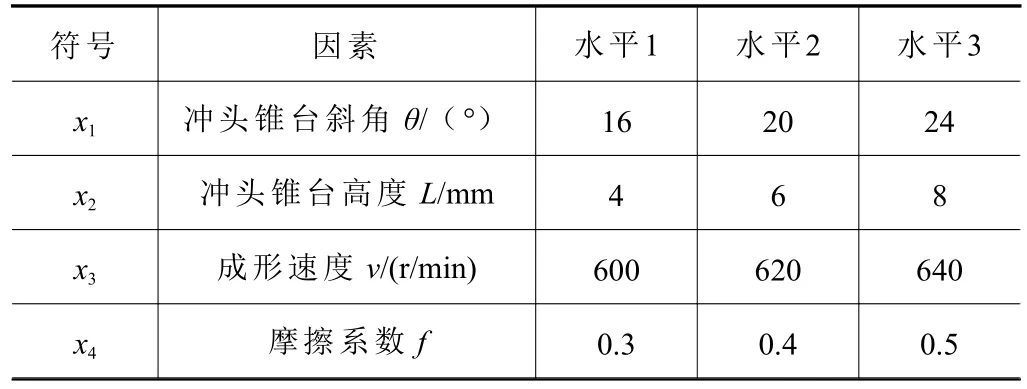
表1 设计变量因素水平表

2 基于Box-Behnken法试验方案设计

响应面法是在科学研究中经常用到的一种工艺优化，实验条件优化的方法，其相对于正交试验法，可以连续地对实验的各个水平进行分析，所得结果更加合理、可靠。响应面分析法一般分为响应面中心复合设计法和 BBD（Box-Behnken design）两种试验设计，为了减少试验次数，缩短试验时间和避免盲目性，得到较好的试验结果[8]，选用BBD试验设计法更为合理。本文选取4个自变量为试验因素，设计以成形载荷大小为响应目标的自攻螺钉冷挤压工艺参数优化试验方案。根据BBD设计方法对表1中的4个因素进行通用旋转组合设计，得到29组不同试验因素的试验方案，以成形载荷为目标对每个方案进行数值模拟，试验方案和结果如表2所示。

表2 试验方案及其响应目标

3 工艺参数优化

利用二阶响应回归模型建立4因素3水平的预测模型，通过最小二乘法对试验结果进行回归分析，得到目标函数响应方程为：

式中：F为成形载荷；x1为冲头锥台斜角θ，°；x2为冲头锥台高度L，mm；x3为挤压速度V，r/min；x4为摩擦系数f。根据设计变量对响应模型进行方差分析检验响应模型的可靠度，方差分析结果如表3所示。

表3 方差分析

根据表3回归方程方差分析表可知，采用ANOVA方差分析法的模型P值远小于0.000 1，说明得到的二阶响应模型是显著的。模型中各影响因素对成形载荷的影响是显著的，其中影响最显著的是x1（冲头锥台斜角θ）和x3（挤压速度v）。通过方差分析表可知，影响成形质量的因素显著性：v＞L＞θ＞f。模型决定系数为0.973 6，说明该模型较好地反应了目标函数的变化，RAdj2=0.922 6，表明整个模型拟合程度较好。通过Design-expert10.0.7软件获得冷挤压成形工艺最优参数组合为：冲头锥台斜角θ=20.16°、锥台高度L=6.12 mm、成形速度v=616.28 r/min、摩擦系数f=0.36。

4 试验验证

基于初步给定参数和最优参数组合设计两组冷挤压成形对比试验，两组均采用两层和三层6061铝合金板材，分别给成形板材贴上应力贴片，通过计算机连接应力贴片，从而连续获取试验过程中的成形载荷，如图4所示。最终得到在初步给定参数下最大成形载荷为17.2 kN，最优参数组合下最大成形载荷为15.1 kN，相较于初步给定参数下最大成形载荷和优化设计目标中的最低成形载荷（通过响应面法数值模拟分析得出）分别降低了13.91%和10.13%，有效降低了成形载荷，如图5所示。通过三层铝合金板材对比试验可知，最优参数同样适用于其他多层冷挤压成形。同时根据试验中金属流动规律可知，螺纹孔残余切屑向上下孔外侧聚集，极大减小了螺纹孔内壁成形载荷，提高了螺纹孔的成形质量，增强了自攻螺钉的连接强度。

图4 试验方案图

图5 冷挤压试验成形载荷

5 结语

（1）利用响应面法建立了以自攻螺钉冷挤压成形螺纹孔为研究目标，冲头锥台斜角、锥台高度、挤压速度和摩擦系数4个因素为试验变量的二阶响应模型，最终获得理想的成形载荷。

（2）根据响应面方差分析法得到影响成形载荷的显著性为：挤压速度v＞锥台高度L＞冲头锥台斜角θ＞摩擦系数f。同时利用Deform-3D软件验证了在冲头锥台斜角θ=20.16°、锥台高度L=6.12 mm、成形速度v=616.28 r/min、摩擦系数f=0.36的最优参数组合下成形载荷能够有效降低。

（3）采用此种优化工艺参数能够有效减少切屑在螺纹孔中聚集，防止螺纹孔内壁崩裂，为其他旋转冷挤压成形工艺提供了一定的参考。