超精密机床热形变及其对运动精度的影响研究
陈熠 王振忠 雷鹏立 施晨淳
(厦门大学航空航天学院,福建 厦门 361005)
超大口径超精密光学元件加工是一个复杂的系统性工程,其发展与一个国家的高端制造技术及装备发展能力息息相关,也是一个国家综合国力的集中体现[1-2]。大口径非球面光学元件在航空航天、军用光学和激光技术等高新技术领域中应用十分广泛[3-7],其典型应用领域之一便是激光核聚变装置。美国国家点火装置(NIF)是当今世界上规模最大的激光惯性约束核聚变装置[8],其所需的大口径超精密非球面光学元件数量超过7 000件[9-10]。相应的,我国神光III激光聚变装置也在研制当中,其对大口径超精密非球面光学元件也存在着巨大的需求。在此背景下,针对大口径光学元件高质量及高效率加工装备的研发迫在眉睫。
美国自20世纪60年代便开始研制超精密机床,推出了DTM、LODTM等超精密机床,其中DTM-3最大加工光学元件口径为2 100 mm,面型精度<30 nm;LODTM可加工最大光学元件口径为1 625 mm,机床精度约50 nm,其超精密加工技术处于世界顶尖水平。英国Cranfield研究所研发的OAGM-2500机床最大加工光学元件口径可达2 500 mm,面型精度<1 μm,是当时世界公认最大加工口径的大型超精密机床[11]。近年,国内在相关项目的驱动下也加强了相关加工装备开发及加工工艺探索。2002年,北京航空精密机械研究所研制出了Nanosys-300非球面超精密复合加工机床,最大加工能力为650 mm,磨削面型精度可达0.3~0.6 μm;2004年,国防科技大学设计制造的大型龙门框架式5轴非球面加工机床AOCMT,可加工最大光学元件直径600 mm,面型精度优于0.6 μm[2];2016年,西安交通大学联合哈工大、厦门大学等单位研制出了最大加工能力为1 500 mm的非球面超精密车磨复合加工机床,可实现所加工元件面型精度小于5 μm,RMS小于10 nm[12]。由此可见,在相关项目的推动下我国在加工大口径非球面光学元件的超精密机床方面已经有了不小的进步,但仍与西方国家有一定的差距,尤其是在加工直径1 500 mm以上光学元件的超精密加工机床上仍然属于一片空白。自主研发超大口径超精密加工机床于当前阶段具有极大现实意义。
对于长时间作业的超精密加工机床,机床热形变误差已经成为精密和超精密加工过程中的主要误差来源[13-14]。机床热形变对机床加工的影响集中体现在加工精度上,它包括机床的几何精度和定位精度2个方面。为了保证所加工零件的精度要求,必需采取相应的措施来降低机床因热形变所受到的影响[15]。因此,针对机床热形变引起的误差分析[16-19]具有十分迫切的意义。
本文以课题组正在研制的可加工光学元件口径1 500 mm的龙门式大口径磨削机床与5轴柔性气囊抛光机床(直线度精度指标均优于1 μm/300 mm)为研究对象,基于有限元方法对机床内部热源引起的机床热形变进行了仿真分析。同时,针对磨削机床所用液体静压导轨和抛光机床所用直线导轨2种不同导轨的热源及其影响进行了热-结构耦合仿真,并对实际机床进行了运动误差的测量。分析所得结果对加工过程中的热误差补偿具有一定指导意义。
1 大口径超精密机床热误差分析理论
1.1 大口径超精密机床热源分析
机床热源主要可以分为内热源和外热源,内热源来自于机床工作过程,如导轨运动过程生热;而外热源来自于机床所处的外部环境,如气温、光照及其他设备发热影响。由于超精密机床一般放置于恒温车间,受外热源影响较小,因此本文主要针对机床内热源进行分析,研究超大口径超精密机床导轨部件生热对机床整体的影响;针对所设计的大口径磨削机床(图1a)及大口径气囊抛光机床(图1b)进行仿真分析研究其热形变及产生的热误差。由于大口径磨削机床采用液体静压导轨,而大口径气囊抛光机床采用直线导轨,因此需要针对2种不同的导轨建立不同的生热模型探究其热影响规律。

图1 大口径磨削机床和大口径气囊抛光机床
(1)直线导轨热源分析
直线导轨在分析其热源时主要考虑导轨与滑块间的摩擦生热,在机床运行过程中导轨与滑块接触面所产生的摩擦热以热传导的形式传递至整机。摩擦生热的表达式为
其中:μ为动摩擦系数,F为压力载荷,v为相对速度。
(2)液体静压导轨热源分析
液体静压导轨具有低摩擦阻力的特点[20],因此摩擦生热并非其主要热源。液体静压导轨的主要热源来自油膜生热,主要包括剪切油膜消耗的功率和液压油流动时消耗的功率,即油泵的输出功率[21]。升温的油膜与导轨面直接接触,通过热传导引起导轨面温度升高导致导轨面发生热形变。文献[22]指出液体静压导轨运动直线度受上下导轨面形影响,其中下导轨面形影响占主导。
1.2 大口径超精密机床传热机制
机床热分析主要遵循热力学第一定律和傅里叶定律。封闭系统的热力学第一定律表达式为
其中,Q为热能,W为功,U为系统内能,KE为系统动能,PE为系统势能。对于稳态热分析,流入系统的热量与流出的热量相等,为
而对于瞬态热分析,流入和流出的热传导率q等于系统内能的变化为
考虑机床工作状态,本文采用瞬态热分析对机床的热形变进行仿真。机床温度场分布满足热传导方程为
其中:u(t,x,y,z)为空间一点在t时刻的温度,k为介质的热传导系数,c为比热容,ρ为密度,g为热源密度。
温度场的边界条件包括:
(1)初始条件,即物体内部温度分布的初始状态。
(2)第一类边界条件,即物体边界的温度μ分布已知。
(3)第二类边界条件,即物体边界上法向热流密度q的情况已知。
(4)第三类边界条件,即物体边界与周围介质的对流换热情况。
其中:h为2种物质热交换系数,θ(t,x,y,z)为外界温度。
在大气环境中,不考虑压强的变化,物体热形变可以用线度代替体积来描述,当温度变化不大时有
式中:ΔL为变形量;L为原始尺寸;α为线膨胀系数;Δu为温差。
2 大口径超精密机床热-结构耦合仿真分析
在大口径超精密机床加工过程中,由于机床热形变所引起的误差高达40%~80%[13]。机床热形变所引起的各个空间位置变化,将对运动部件的定位误差、角度误差,特别是直线度误差产生直接的影响[23]。在机床设计阶段,针对机床导轨生热引起的机床热形变进行分析,能够为机床制造及使用阶段提供相应的热误差补偿参考措施。
(1)磨削机床热仿真分析
大口径磨削机床采用液体静压导轨,摩擦生热较小,故仿真分析将油膜的温度升高作为内部热源,在考虑内部热源引起机床温升的同时,也考虑机床在恒温环境中对外散热。故热源载荷为升温的静压导轨油膜,边界条件设置为机床表面空气对流,仿真机床初始温度21 ℃,通过前期实验数据采集,设油膜升温2 ℃,空气温度21 ℃,油膜对流交换系数为300 W/(m2· ℃),仿真时间为80 000 s。利用ANSYS Workbench瞬态热模块进行仿真,磨削机床内部热源瞬态热仿真温度分布结果如图2所示,由温度分布云图可以看出,整机导轨处及附近区域的温升明显,左右立柱温度在恒温环境下基本保持不变。

图2 磨削机床内部热源瞬态热仿真温度分布结果
(2)抛光机床热仿真分析
大口径气囊抛光机床采用直线导轨,在运动过程中导轨摩擦生热为其主要热源,故热源载荷为导轨摩擦生热值,边界条件设置为机床表面空气对流,仿真机床初始温度21 ℃,空气温度21 ℃,仿真时间为80 000 s。根据摩擦生热公式,需要对各滑块的压力载荷进行分析。抛光机床工作台所在轴共有4条直线导轨,每条导轨等距分布4个滑块,分析时考虑工作台重力均匀分布在16个滑块上,因此滑块与导轨间压力载荷均为3 466.2 N,工作台进给速10 000 mm/min,根据摩擦系数和负荷荷重比关系曲线,计算得其动摩擦系数为0.005,由摩擦生热公式可得单个滑块与导轨接触面的摩擦生热功率为2.9 W。对于龙门横梁导轨的滑块,由于龙门结构存在压弯特性,以及主轴箱的偏载,故导轨各滑块压力分布具有非均匀的特征。采用ANSYS Workbench静力学分析模块对横梁处导轨滑块的正压力载荷进行仿真计算。导轨两端设置固支约束,在自重载荷下仿真横梁上6个滑块的正压力,如图3所示。
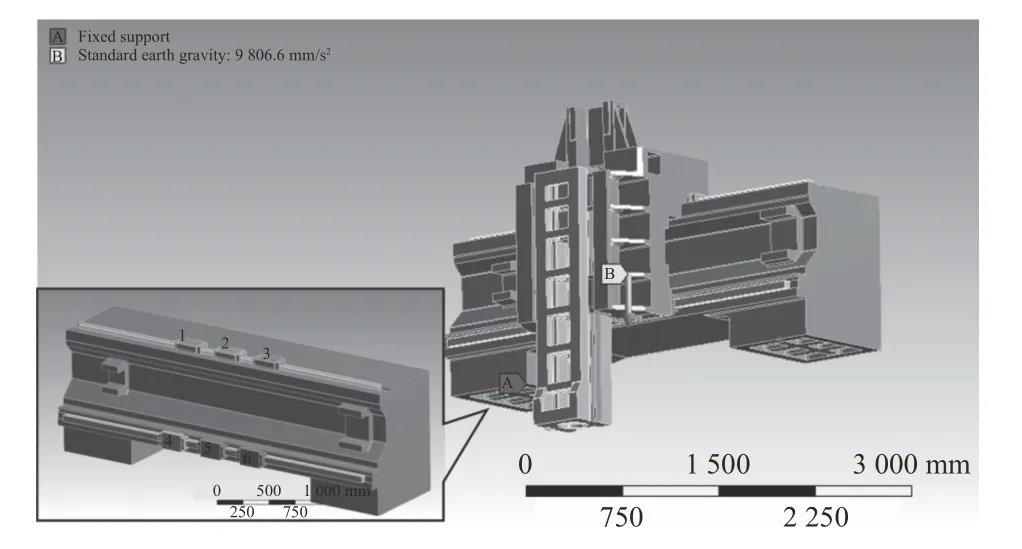
图3 气囊抛光机床横梁静力学仿真
表1给出了横梁导轨滑块1~6对应的正压力仿真结果及其对应的动摩擦系数。

表1 横梁静力学仿真结果
本文分析中设置摩擦生热分配比为1:1,即导轨与滑块在接触面分别流入50%的摩擦热能。为仿真机床运动部件在一段时间内沿导轨往复运动,考虑将流入导轨的摩擦热流量在导轨面上均匀分布。抛光机床内部热源瞬态热仿真温度分布云图如图4所示,由温度分布云图可以看出,气囊抛光机床整机导轨及滑块处附近区域的温升明显,左右立柱的温度在恒温环境下基本保持不变。在80 000 s(约24 h)的持续运动中,整机最高温度上升到了21.485 ℃,表明采用直线导轨的气囊抛光机床在空载持续运行24 h的情况下,由于导轨摩擦造成的导轨最高温升为0.485 ℃。

图4 抛光机床内部热源瞬态热仿真温度分布结果
(3)机床热形变仿真分析
在静力学模块中将磨削与抛光机床内部热源的瞬态热分析结果作为载荷加载,对磨削与抛光机床进行热形变仿真,仿真结果如图5所示。

图5 内部热源引起的机床总形变
可以看出机床内部热源会造成机床整机部件的热膨胀,磨削机床最大热形变为42.4 μm,气囊抛光机床最大热形变为7.3 μm。其结果表明在相同的环境温度与运行时间下,采用直线导轨的气囊抛光机床整机热形变比采用液体静压导轨的磨削机床小。针对磨削机床在不同油膜温升的情况下进行磨削机床热形变仿真分析,其油膜温升对机床热形变的影响规律如图6所示。
从图6可以看出,油膜温升与机床最大热形变呈线性相关,若在机床运行过程中能够较好地控制油膜温度,将在很大程度上改善其对机床产生的热形变影响。因此,在实际机床调试阶段,可以针对液体静压导轨液压油冷却循环系统进行相应预设值补偿,通过设定油冷系统冷却温度来控制进入导轨液压油的初始温度,从而降低油膜生热造成的机床运动误差。

图6 油膜温升对机床形变的影响规律
分析机床加工工具头及工作台台面在80 000 s持续运行过程中的相对位移误差,可以得出磨削机床的加工工具头与工作台的间距减小5.3 μm,气囊抛光机床加工工具头与工作台间距减小2.2 μm。故在整机设计阶段,通过有限元热-结构耦合仿真可以得出磨削机床由于导轨部件热源影响,将造成机床实际加工过程中加工点与工件距离缩短效应,其误差在5 μm左右。
3 机床导轨热误差测量实验
如图7a所示,磨削机床工作台所在轴采用液体静压导轨;如图7b所示,抛光机床工作台所在轴采用直线导轨。为探究实际热源引起的机床热形变对超精密机床运动误差的影响,对超精密磨削机床与气囊抛光机床进行关键点温度监控,并利用电子水平仪对机床导轨运动直线度进行测量。测量运动直线度时,固定电子水平仪后移动静压导轨与直线导轨走完一个行程,分段测出不同位置的水平仪读数,通过软件拟合成直线度曲线,电子水平仪布置位置如图7c所示。温度传感器采用PT100铂热电阻,设置测点为静压导轨进、出油口、直线导轨滑块以及直线导轨座,如图7d所示。

图7 测量实验
磨削机床与抛光机床放置于恒温车间,开机后即对磨削机床所用液体静压导轨与抛光机床所用直线导轨的直线度进行初始直线度测量;测量完初始直线度后保持机床开启,待机4.5 h后对液体静压导轨与直线导轨的直线度进行第2次测量;随后开启机床空跑程序,让液体静压导轨与直线导轨往复运动5 h后对直线度进行第3次测量;在实验过程中,始终对液体静压导轨进出油口及直线导轨滑块与直线导轨座进行温度采集。实验流程如图8所示。

图8 实验流程设计
实验采集的温度传感器各布点的温度变化曲线如图9所示,可以看出,直线导轨、滑块及出油口的温度均在20~21 ℃附近且变化不大;进油口的温度在短时间内急剧升高到25 ℃附近后趋于平缓,这是由于液压泵输出功率导致液压油在进入导轨前产生了4 ℃左右的温升。

图9 关键布点温度变化曲线
如图10所示,针对液体静压导轨出油口、直线导轨滑块、直线导轨底座3处测温点在待机和空跑下的温度数据进行分析。磨削机床液体静压导轨出油口处液压油温度整体呈线性上升趋势,且在待机状态和空跑状态下的趋势较为一致。而抛光机床直线导轨滑块及导轨底座在待机状态下温升不明显,开启空跑程序后温度呈线性上升,整体温升曲线存在明显的拐点。这是由于直线导轨热源主要来自摩擦生热,待机状态下不存在导轨滑块与导轨底座相对运动,开启空跑后摩擦生热成为主导,故产生温升曲线的拐点。实验过程中3次测量的导轨运动直线度如图11所示。初始时刻,机床在恒温车间自然稳定状况下,液体静压导轨与直线导轨的运动直线度均小于1 μm。在整个实验流程中,直线导轨的运动直线度相对保持稳定;静压导轨运动直线度呈明显上升的趋势,最终的运动直线度为4 μm。这表明液体静压导轨在待机状态及空跑状态下产生了较大的热形变,因此在实际加工工程中,需要针对液体静压导轨及直线导轨不同的运动直线度误差变化做出相应的补偿措施。
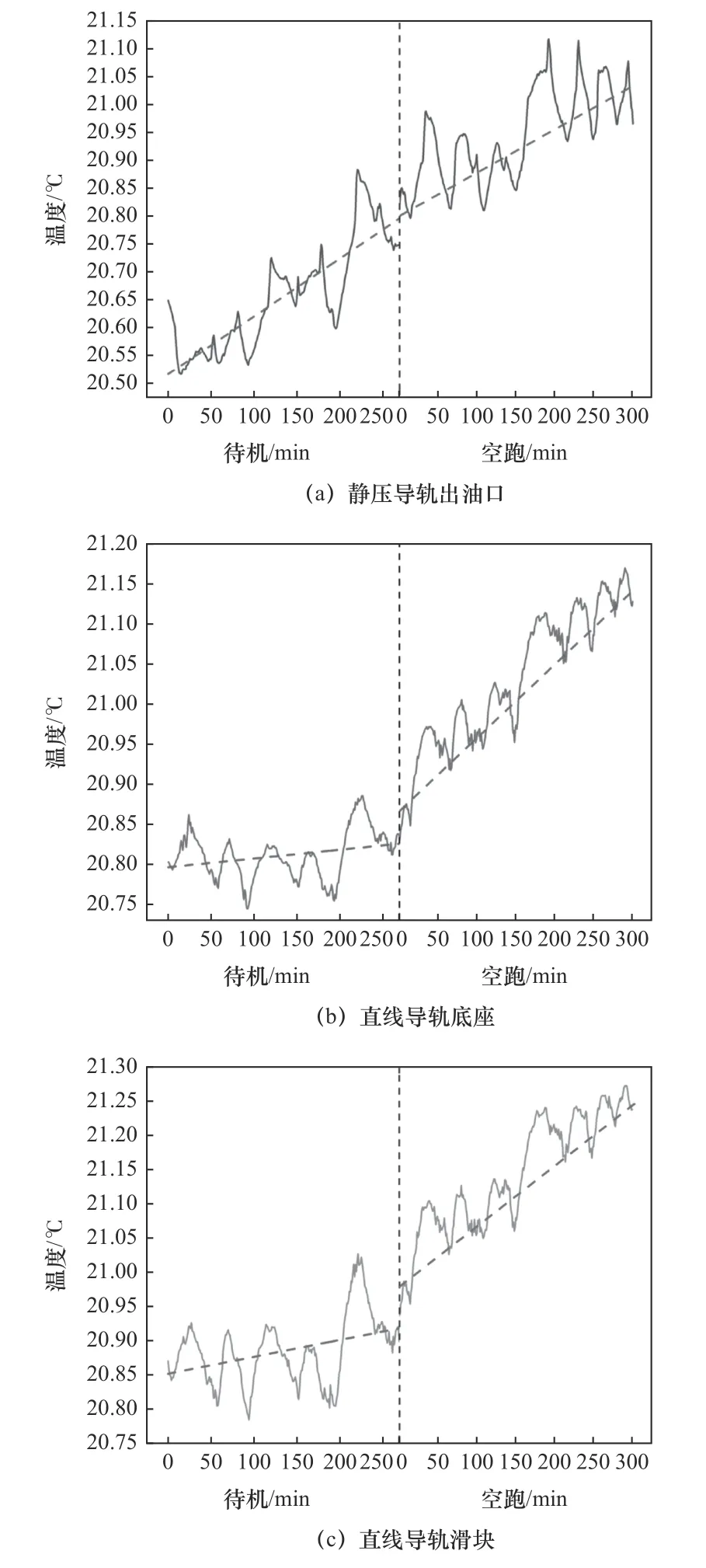
图10 实验不同阶段关键布点温度变化曲线

图11 静压导轨与直线导轨运动直线度变化情况
机床热误差补偿主要分为两种途径:一种是通过设计、制造和装配反向弥补热误差,该方法成本较高,对整体基础工业水平的依赖较强;另一种是通过软硬件结合,对机床热误差进行实时预判,驱动伺服系统进行外部机械原点偏移,从而抵消运动误差。因此,可利用布置在机床关键节点上的温度传感器实时采集温度信号,通过建立热误差数据库,结合离线的有限元仿真作为参考,建立实时的热补偿算法,从而计算出理论误差补偿值进行补偿。
4 结语
(1)超精密机床的热形变对机床运动误差具有较为明显的影响。热形变会造成磨削机床和抛光机床的导轨运动直线度发生变化,同时机床其他部件也会产生一定形变,导致实际加工点与工件间的距离发生变化,从而影响大口径光学元件的加工精度。
(2)超精密机床内部热源主要集中在导轨处,液体静压导轨主要热源为液压油生热,直线导轨主要热源为导轨摩擦生热。针对所设计的大口径超精密磨削机床以及大口径气囊抛光机床,利用有限元仿真分析了导轨热源造成的机床整机热形变影响规律。结果表明在相同环境温度与运行时间下,采用直线导轨的气囊抛光机床整机热形变比采用液体静压导轨的磨削机床小。在导轨热源的作用下,机床加工工具头与工作台台面间距会减小。
(3)机床温度-直线度监测实验结果表明:在相同的工作条件下,液体静压导轨运动直线度变化比直线导轨更加明显。由于液压泵的输出作用,液体静压导轨进油口处的油温在开机后迅速上升,从而引起液体静压导轨发生热形变,导致导轨直线度发生变化。而直线导轨在静止时基本无热源,在加工运行中虽有导轨摩擦生热,但温升较为缓慢,对导轨运动直线度没有明显影响。

