钛合金型面侧壁铣削力建模与仿真＊

李安海 朱晓丽 张茹凤 盖少磊

（①山东大学机械工程学院高效洁净机械制造教育部重点实验室，山东 济南 250061；②机械工程国家级实验教学示范中心（山东大学），山东 济南 250061；③德州大陆架石油工程技术有限公司，山东 德州 253034；④滨州渤海活塞有限公司，山东 滨州 256602）

钛合金由于高强度重量比和好的耐腐蚀性能等性能特点，广泛应用于航空航天等领域，而钛合金复杂整体结构零件通常由侧壁、腹板和不规则框架组成，材料去除量大且因受力情况难以控制容易产生弹性变形[1]。特别是侧面壁板型面结构加工过程中，由于铣削力的作用下会产生“让刀变形”，从而影响加工过程的稳定性及加工表面质量[2]。因此，需对钛合金型面侧壁铣削力进行有针对性地研究，从而控制钛合金薄壁件或型面结构件铣削加工变形。

切削力不仅会对表面粗糙度、加工硬化程度、残余应力和微观结构等加工表面质量特征参数产生不可忽视的影响[3]，还会严重地加剧刀具的磨损程度导致其使用寿命有所缩短[4]。铣削力建模研究可以有效预报切削加工过程铣削力，有助于更好地理解金属材料加工机理。周鑫等人[5]提出了针对复杂结构件特征的切削力建模预测方法，从而实现包含工件局部形状尺寸和切削参数等信息的侧铣切削力快速预测和评价。岳彩旭等人[6]采用Abaqus有限元仿真分析了刀具结构参数对钛合金薄壁件的铣削力的影响，并采用切削试验进行了验证。赵仲林和安立宝[7]通过对比有限元仿真和BP神经网络对铣削力的预测值，证明了BP神经网络具有较高的预测精度。王海艳等人[8]基于斜角切削的切削力系数辨识方法，建立了考虑槽侧刃和底刃的钛合金螺旋铣孔切削力模型，并验证了斜角切削系数辨识方法的有效性。

通过切削力的预测建模，可以估算切削过程中的受力情况，为切削参数范围的合理选择与工艺方案的制定提供了理论依据。

本文基于机械力学理论并结合切削试验，建立了四刃圆柱螺旋立铣刀的瞬态铣削力模型，最后借助于钛合金侧面侧壁铣削试验验证了所建立的切削力预测模型的可靠性。

1 整体立铣刀铣削力建模

整体立铣刀铣削力机械力学建模具体过程是，首先将铣刀切削刃沿其竖直轴线方向分割成若干个的切削微元，其分解几何示意图如图1所示，继而建立起切削微元（i,j）的各向切削力模型，对其进行矢量求和后，通过数值积分和坐标变换，即可进一步确定出铣刀在旋转一周时所受的X、Y和Z三个方向的整体切削力Fx(ϕ)、Fy(ϕ)、Fz(ϕ)。

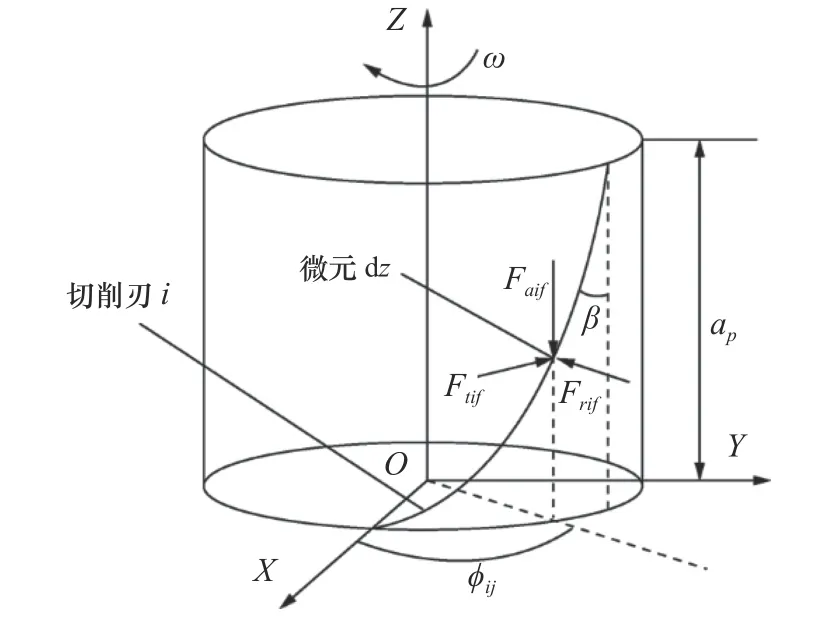
图1 立铣刀切削刃微元分解几何示意图

对于刀具为四刃圆柱螺旋立铣刀，当机床主轴带动刀具旋转参与切削时，由于螺旋角的存在，切削刃在轴线方向上相对于底刃有一个滞后角，则立铣刀半径为R，螺旋角为β，则切深方向高度z处的瞬时切削角 ϕi,j(z)的表达式为式（1）。

式中：ϕ1为刀齿的接触角；ϕp为立铣刀的刀齿齿间角，ϕp=2π/N，N为齿数；i为铣刀的第i个切削刃；j为第i个切削刃上沿刀具轴线方向的第j个切削微元。其中，滞后角 ϕr(z)为

每齿进给量为fz时，切屑厚度h在切削过程中会随切削位置的改变而不断改变，可表示为

由瞬态切削力模型的基本计算公式可知，切削微元（i,j）切向、径向和轴向切削分力dFt、dFr和dFr可以分别表示为

式中：Ktc、Krc和Kac分别为切向、径向和轴向的剪切力系数，Kte、Kre和Kae分别为切向、径向和轴向的刃口犁耕力系数。

如果要判别铣刀在某一瞬间对于任意一微元切削刃是否在参与切削，可由g(ϕi,j(z))断定，其基本原理是根据瞬时切削角 φi,j(z)的位置来判别，也就是说当其瞬时切削角和切入角ϕst及切出角ϕex是否满足条件ϕst≤ϕ≤ϕex。

顺铣时

由铣刀各切削刃微元的空间位置基于坐标变换即可获得各方向切削力分量表达式。

将其沿轴线方向积分，然后将施加在各切削刃微元上的受力进行整体矢量求和，刀具在旋转参与切削时任意时刻整个立铣刀上的切削合力为

2 整体立铣刀铣削力系数辨识

切削力系数最常采用的求解方式主要分为两种，一是基于斜角切削原理，根据刀具基本参数和几何角度变换来计算金属材料铣削加工的切削力系数[8]，由于这种计算方法需要预先假定一些加工外部条件，使用范围不可避免具有局限性，故而几何求解模型的计算精度往往难以保证。另一种方法就是通过实验的方式来确定[9]。该方法主要是在保证其他参数值不变的前提下，只对每齿进给量的数值做出调整，然后设置多组钛合金切削试验，进而对一个周期内平均铣削力的数值求解。在之前大多数研究中，常常较多地采用实验方法确定切削力系数数值。

铣刀的各个刀齿在单位切削时间内试验中去除钛合金工件材料的体积是固定不变的，因此螺旋角β的大小对铣刀平均切削力的数值大小没有影响，因此在基于试验确定切削力系数数值时可以首先初步假定β=0°。因此在铣刀旋转一周内每个刀齿上的平均切削力F可以用铣刀整体切削力与刀具齿间角的比值计算求得，其数学表达式可表示为

则在圆柱立铣刀旋转一周内4个刀齿上各方向平均切削力数学计算表达式可表示为

其中：

因而各方向平均切削力试验值和每齿进给量fz两者之间的数学计算表达式可表示为

式中：各平均铣削分力值可以借助于钛合金铣削力辨识试验来求取，然后使用Matlab软件对各平均切削分力进行数值线性拟合，获得式（11）中变量值，继而即可获得钛合金侧铣试验圆柱螺旋立铣刀各切削力系数的数学计算表达式为

基于Matlab软件编写了四刃整体硬质合金立铣刀瞬时切削力仿真程序，输入切削参数、刀具参数和切削力系数等基本条件即可计算任意参数下圆柱螺旋立铣刀的瞬时切削力，程序流程见图2。

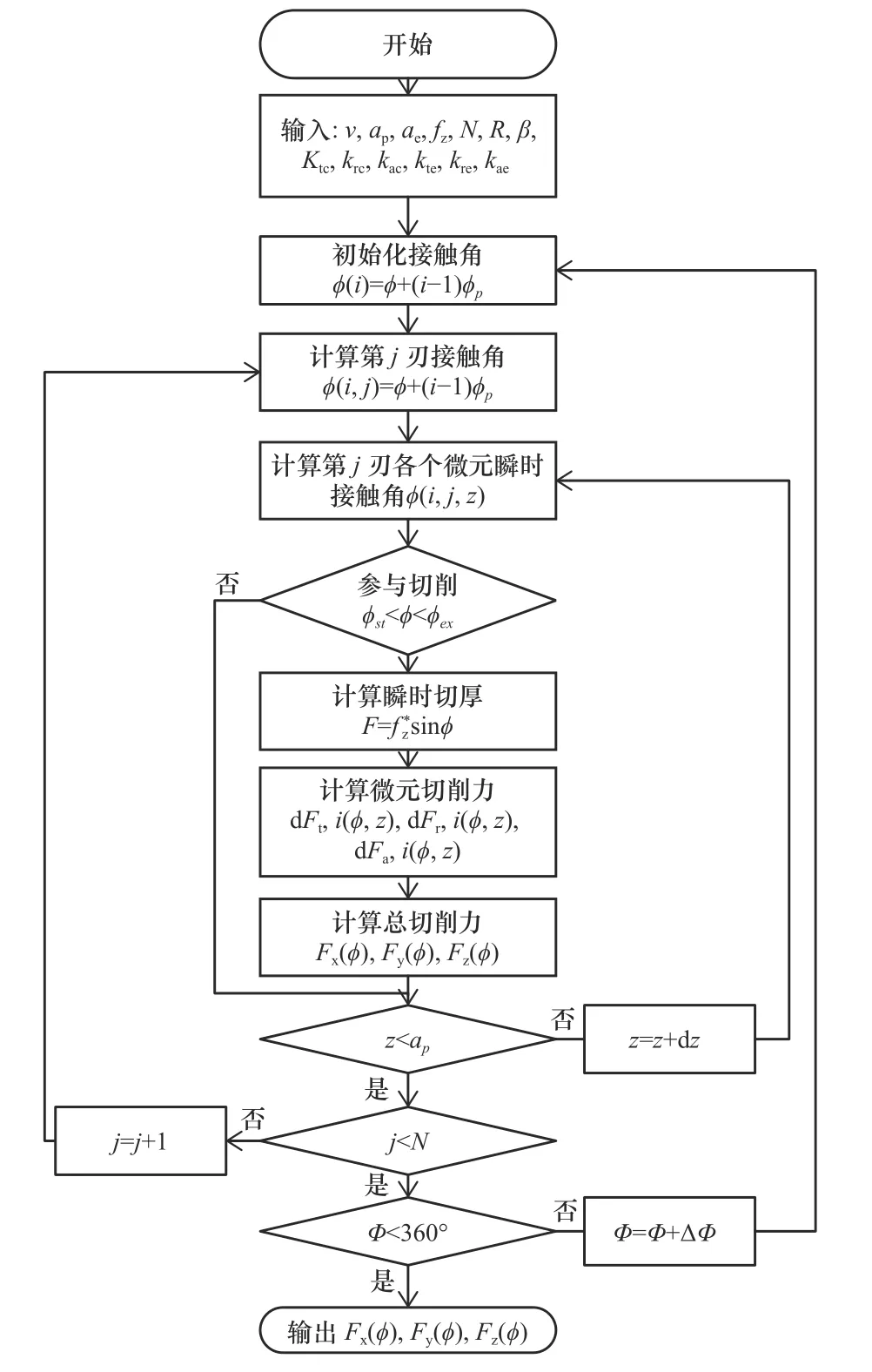
图2 铣削力算法流程图

3 钛合金型面侧壁铣削试验

切削试验所选用的工件材料为钛合金Ti-6A1-4V块料，其属于α+β双相合金，主要化学成分含量百分比见表1，主要物理力学性能参数见表2。

表1 Ti-6A1-4V化学成分

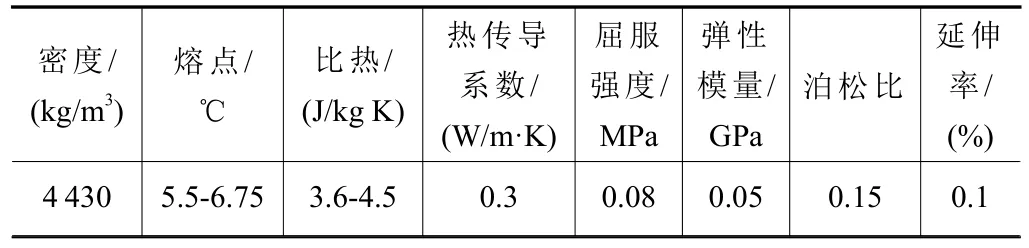
表2 Ti-6A1-4V物理及力学性能

本试验所使用的机床型号为DAEWOO ACE V500立铣床，刀具为实验室自主研制的整体硬质合金立铣刀，其基本性能参数如表3所示，涂层材料为TiAlN复合涂层。加工方式为顺铣，干切削。首先将钛合金工件通过连接件与Kistler 9257B测力装置固定并一同夹紧固定在铣床工作台面上，所测得的切削力信号首先需要经过5070A电荷放大器放大，再经由5697A信号采集器后借助于电脑端安装的DynoWare分析软件记录并保存数值用于实验数据分析。试验装置及测力装置见图3。

图3 试验机床及切削力测量装置

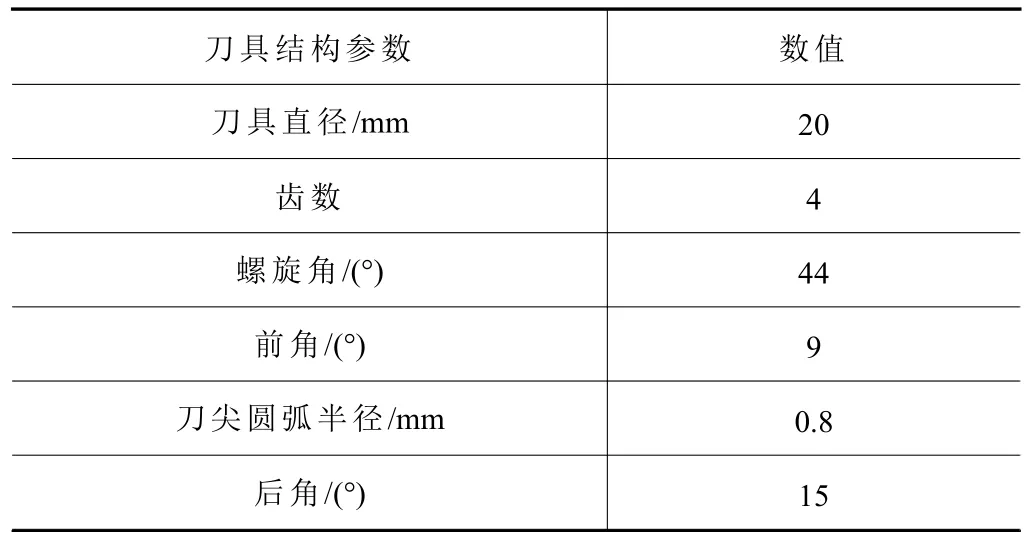
表3 刀具几何参数[10]

每组试验的选取10个峰值切削力并取平均值用于计算微元切削力系数，切削力辨识试验参数设置如表4，经计算所得钛合金工件材料切削力系数见表5。

表4 切削力辨识试验参数

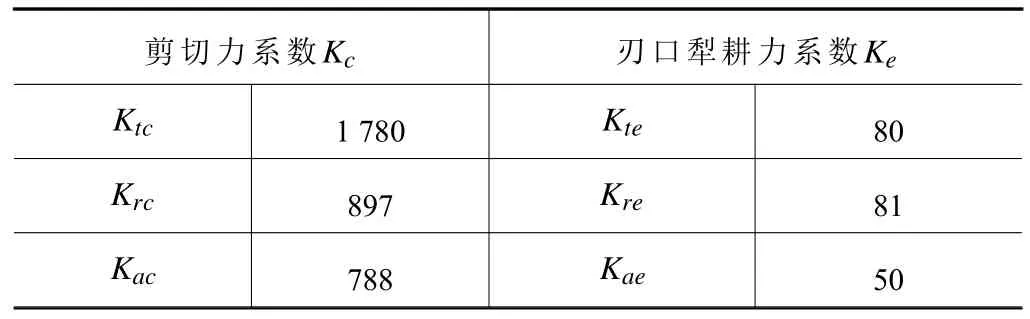
表5 立铣刀铣削力系数

4 铣削力模型验证与分析

随机选择4组铣削参数利用切削试验验证了主切削力多项式拟合的指数公式及仿真切削力预测的有效性。本验证试验中各切削参数设置见表6，主切削力试验值、仿真值及其各自对应的相对误差值见表7。

表6 验证试验切削参数

表7 两种主切削力模型预测误差

图4为试验与仿真模型所得切削力对比图，通过对4组钛合金铣削试验的切削力实测值与仿真值对比，计算可得仿真模型误差在5.56%～15.8%，可见所建立的铣削仿真模型具有较好的准确度，并证明了本文中所提出的有关圆柱立铣刀切削力系数数值计算结果和主切削力预测模型的准确性。

图4 铣削力预测值对比

5 结语

通过对圆柱螺旋立铣刀几何外形分析，将其沿铣刀切削刃划分为若干个切削微元参与切削，进而建立瞬时切削力模型，然后再通过空间坐标变换和数值积分求和等基本操作建立圆柱螺旋立铣刀整体切削力数学计算公式，通过钛合金侧铣试验完成切削力系数辨识，然后借助于Matlab程序完成了切削加工过程瞬态切削力仿真计算。

为验证模型的正确性，设计了钛合金铣削验证试验，仿真与试验结果的一致性证实了两种模型的可靠性，经验证可以得仿真模型误差在5.56%～15.8%，可以较好地用于切削力的预测和参数变量优化，为钛合金型面件侧壁加工过程工艺参数制定和优化奠定了理论基础。