基于MATLAB的直线度测量不确定度评定程序设计

吴呼玲

(陕西国防工业职业技术学院 机械工程学院，西安 710300)

基于MATLAB的直线度测量不确定度评定程序设计

吴呼玲

(陕西国防工业职业技术学院 机械工程学院，西安 710300)

形位误差测量不确定度评定由于其测量的复杂性和测量结果评定的多样性，导致在实际测量结果中形位误差测量的不确定度评定成了难题;尤其是测量点较多，测量数据难以处理，处理结果的准确性难以保证;为此，根据直线度测量不确定度的评定过程对其进行了评定程序的设计，在程序命令的提示下，输入测量值便可得到直线度误差，输入单点测量不确定度便可得到直线度测量不确定度;该程序根据测量不确定度常用的GUM法和蒙特卡罗法思想进行设计，可得到两种不同的评定结果,不受测量点的多少、测量数据的复杂程度等因素影响;通过数据验证，程序可靠准确,为直线度测量不确定度评定提供了便捷、高效的数据处理方法;通过测量数据验证，该程序准确可靠，具有一定的实际应用价值和推广意义。

直线度；不确定度；程序设计

0 引言

直线度误差测量是几何测量中常用到的误差测量项目，它的大小会直接影响到零部件的互换性和产品质量，因而准确、快捷的评定测量结果的不确定度成为一个重要的课题。形位误差测量不确定度的评定方法常用的有：不确定度表示指南[3]提供的通用方法(简称GUM法)和蒙特卡罗法[1]两种。由于形位误差测量的复杂性和多样性，测量数据多、测量结果位数多、处理结果准确性难以保证，通过计算机程序对其进行处理成了解决问题的关键。

本文选用最小二乘法建立直线度误差模型，依据GUM法和蒙特卡罗法评定直线度测量结果不确定度的评定过程进行分析，根据评定过程与评定原理进行程序设计，并进行数据验证，确定程序的正确性。因此编制基于Matlab的直线度测量不确定度评定程序，程序处理时间段、计算精度大大提高，使数据处理方便可靠。为后续其他形位误差的评定奠定了一定的基础，为其他形位误差的测量不确定度评定的程序设计提供了相应的方法，具有实际的应用前景。

1 最小二乘法建立直线度误差模型[5]

(1)

(2)

(3)

2 GUM法评定直线度测量结果不确定度的过程

1)求出(3)式中直线度误差模型各参数的传递系数:

(4)

(5)

(6)

(7)

(8)

2)各参数测量不确定度分别为：

u(xM)=u(yM)=u(xL)=u(yL)=u0

(9)

其中:u0为某种具体测量过程中测量不确定度主要来源的多个方面，各个方面的不确定度分量的合成不确定度。例如，三坐标测量机测量芯轴素线的直线度，各参数的测量不确定度u0=1.56 μm。

(10)

直线度误差测量不确定度评定公式[2]为：

(12)

3 蒙特卡罗法评定直线度测量结果不确定度的过程

1)根据具体的测量过程和采用的测量设备，分析测量过程中的不确定度来源。计算出直线度测量任务中，直线度的单点测量不确定度。

2)确定直线度误差模型中各参数：xM；xL；yM；yL；k的期望和方差(期望为各参数的测量值，方差为各参数的单点测量不确定度)。

3)以xM；xL；yM；yL；k参数的期望和方差生成五维随机数来模拟直线度误差的测量值[6]，样本容量为M，采用大样本进行直线度误差的测量不确定度评定。生成的五维随机数分别为：xM1，xM2，xM3，……xMM；xL1，xL2，xL3，……xLM；yM1，yM2，yM3，……yMM；yL1，yL2，yL3，……yLM；k1，k2，k3，……kM；

4)根据以上随机序列，带入直线度误差模型公式，求出M个直线度误差f的值，根据这组f的值，构造一个概率分布。判断分布类型求出方差，即为所要求的直线度误差测量标准不确定度。

4 基于MATLAB的直线度测量不确定度评定程序设计

%直线度不确定度评定[4]程序

clear;

clc;

A=xlsread('测量数据20170219.xls');

A1=A(:,1);

A2=A(:,2);

n=size(A1);

b=(sum(A1.*A2)*sum(A1)-sum(A1.*A1)*sum(A2))/(sum(A1)*sum(A1)-n(1,1)*sum(A1.*A1))

%直线常数

k=(sum(A1)*sum(A2)-n(1,1)*sum(A1.*A2))/(sum(A1)*sum(A1)-n(1,1)*sum(A1.*A1))

%直线系数

for i=1:n(1,1)

d(i)=(A2(i)-(k*A(i)+b))/sqrt(1+k^2);%最小二乘直线的距离

End

D=A1;

D=d

plot(A1,k*(A1)+b)

hold on

plot(A1,A2);

[maxd,dM] = max(d)%距离最大值及位置

[mind,dL] = min(d)%距离最小值及位置

f=(A2(dM)-A2(dL)-k*(A1(dM)-A1(dL)))/sqrt(1+k^2)%直线度误差

fxM=-k/sqrt(1+k^2);%计算传递系数

fzM=1/sqrt(1+k^2);

fxL=k/sqrt(1+k^2);

fzL=-1/sqrt(1+k^2);

fk=(A1(dM)-A1(dL))/sqrt(1+k^2);

u0=input('单点测量不确定度u0(cm):');%输入参数参数值

uzL=u0;

uxL=uzL;

uzM=uxL;

uxM=uzM;

for i=1:n(1,1)

kz(i)=(sum(A1)-n(1,1)*A1(i))/(sum(A1)*sum(A1)-n(1,1)*sum(A1.*A1));

end

uk=sqrt(sum(kz.*kz)*u0^2);

uf=sqrt((fxM*uxM)^2+(fxL*uxL)^2+(fzM*uxM)^2+(fzL*uzL)^2+(fk*uk)^2)%直线度误差测量的不确定度

%生成服从正态分布的五维随机数

M=input('样本容量M:');%输入参数参数值

XM=normrnd(A1(dM),u0,1,M);

XL=normrnd(A1(dL),u0,1,M);

ZM=normrnd(A2(dM),u0,1,M);

ZL=normrnd(A2(dL),u0,1,M);

KM=normrnd(k,uk,1,M);

for i=1:M

fM(i)=(ZM(i)-ZL(i)-k*(XM(i)-XL(i)))/sqrt(1+k^2);

end

figure(2),histogram(fM)

fjun = mean(fM)

fcha=std(fM)

5 程序运行过程及结果

使用爱德华公司的MQ686型三坐标测量机对一根芯轴的素线进行直线度测量[7]，输入测量结果，通过程序直接给出评定结果。被测工件长度180 mm，在X轴方向均匀取10个点，每个点间隔10毫米进行坐标测量[10]，测量结果如表1所示。

表1 三坐标测量机测量芯轴素线直线度数据

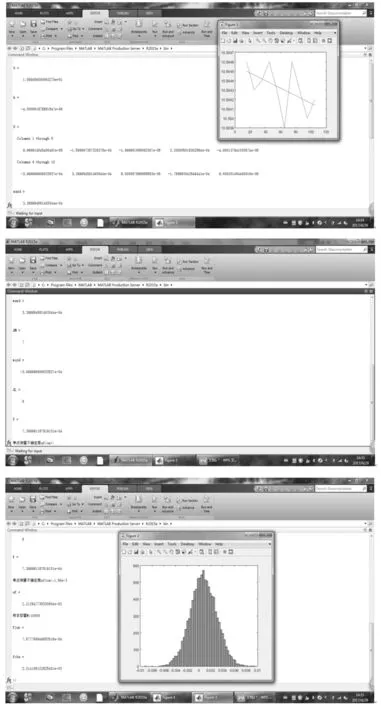
程序运行结果显示：

1)最小二乘直线方程y=kx+b的待定系数k和b的值。

2)被测要素上测量取样点(xi，yi)至直线L的距离为Δi(i=1,2,…,10)，并显示出被测直线要素的的实际误差和最小二乘直线。

3)距离最小二乘直线最高距离的点坐标和点的标号，距离最小二乘直线最低距离的点坐标和点的标号。

4)直线度误差值。

5)当程序提示输入单点不确定度数值后，程序算出直线度测量不确定度。

6)利用蒙特卡罗法计算直线度测量不确定度时，需要样本容量M。输入样本容量是10000时，程序通过蒙特卡罗原理，给出直线度误差(期望)和直线度测量不确定度(方差)。并给出正态分布曲线图。

程序运行过程中的参数说明：

1)由于测量过程和测量方法不同，采用的测量设备也不同。因此需要根据实际测量情况，分析测量过程中的不确定度来源，并给出单点不确定度数值，在程序运行过程中需要手工输入，可对同的单点不确定度数值的测量不确定度结果进行评定。

2)蒙特卡罗法进行伪随机数模拟时，需要样本容量。根据实际情况给出样本容量的大小。因此需要手工输入，以便给出合适的样本容量。

6 程序正确性验证

通过GUM法对直线度测量不确定度的评定过程[8]，采用EXCEL表格的手工计算，对三坐标测量机测量的结果进行直线度误差计算和不确定度结果评定，评定结果与计算机程序的运行结果一致。

1)EXCEL表格的手工计算直线度误差和测量不确定度结果[9]：

直线度误差f=0.738 μm≈0.74 μm

直线度测量不确定度uf=2.2126 μm

2)计算机程序运行结果的直线度误差和测量不确定度结果：

(1)GUM法的运行结果为：

直线度误差f=0.7399 μm≈0.74 μm

直线度测量不确定度uf=2.2128 μm

(2)蒙特卡罗法的运行结果为：

直线度误差f=0.75776 μm≈0.76 μm

直线度测量不确定度uf=2.2142 μm

7 结语

用EXCEL表格手工计算和通过编写程序进行程序运行，对直线度误差和测量不确定度进行评定。其评定结果相同。由此可见，通过计算机编程对直线度误差和测量不确定度进行结果评定结果可靠、便捷、高效等优点值得推广和应用，也为其他形位误差测量不确定度评定的程序编写鉴定了一定的基础。具有工程实用价值和测量领域数据处理方面的应用前景。

[1] 周桃庚.用蒙特卡洛法评定测量不确定度[M].北京:中国质检出版社,2013.

[2] 倪骁骅.形状误差评定和测量不确定度估计[M].北京:化学工业出版社,2008.

[3] JJF1059.1-2012.测量不确定度的评定与表示[S].

[4] 林志熙，周景亮.基于MATLAB的直线度误差数据处理的研究 [J].工具技术,2008,42(3)：84-87.

[5] 黄富贵，崔长彩.评定直线度误差的最小二乘法与最小包容区域法精度之比较 [J].光学精密工程,2007,15(6)：889-893.

[6] 田树耀，黄富贵，田 辉，等.一种基于MATLAB的形位误差评定方法 [J].工具技术,2008,42(4)：95-97.

[7] 黄富贵，郑育军.直线度误差测量采样方案的研究 [J]. 工具技术,2007,41(10)：95-98.

[8] 刘存成，胡 畅.基于MATLAB用蒙特卡罗法评定测量不确定度[M].北京:中国质检出版社，中国标准出版社, 2014.

[9] 费业泰.误差理论与数据处理[M].北京:机械工业出版社,2012.

[10] 何 频，郭连湘.计量仪器与检测[M].北京:化学工业出版社,2006.

Program Design of Linear Measurement Uncertainty Evaluation Based on Matlab

Wu Huling

(School of Mechanical Engineering, Shaanxi Institute of Technology, Xi′an 710300, China)

Because of the complexity of the form and position error of measurement and measurement results of diversity, lead to actual measurement result of form and position error measurement of the uncertainty evaluation has become a problem.In particular, the measuring points are more, the measurement data is difficult to deal with, and the accuracy of processing the result is difficult to guarantee.In this paper, the evaluation process of the uncertainty based on the straightness measurement is designed.At the prompt of the program command, the linear degree error can be obtained by the input measurement value, and the uncertainty of the linear degree can be obtained by the input single point measurement uncertainty.The program is designed based on the method of using the GUM method and the Monte Carlo method, which is used to measure uncertainty, and can be obtained by two different evaluation results.The degree of unmeasured and the complexity of measuring data is affected. Through data verification, the program is reliable and accurate.It provides convenient and efficient data processing method for measuring uncertainty of linear degree.By measuring data verification, the program is accurate and reliable, and has certain practical application value and extension significance.

straightness; uncertainty; programming

2017-04-30；

2017-06-05。

吴呼玲(1979-)，女，陕西临潼人，硕士，讲师，主要从事机械产品检验检测、误差理论与数据处理、机械设备状态监测等方面的教学和研究工作。

1671-4598(2017)12-0288-03

10.16526/j.cnki.11-4762/tp.2017.12.074

TH124

A