WSN中基于灰狼和差分进化的簇首选择算法

张 新，俞宗佐

(内蒙古师范大学 计算机科学技术学院，内蒙古 呼和浩特 010000)

0 引 言

无线传感器网络(wireless sensor network，WSN)[1]中节点由电池供电，大多数情况下无法及时补充能量，因此，对WSN设计能量均衡策略以延长网络生命周期具有重要意义。

LEACH协议的簇首选择是随机的，导致所有节点的总能量消耗既不平衡也不最小化[2]。LEACH-E协议将节点剩余能量的影响因素加入到簇首选择的概率中[3]，但是，该协议仍然使用随机的方式选择簇首。WSN成簇和簇首选择问题属于NP难问题[4]，不易求解。近年来，有研究者用群体智能算法来优化WSN分簇与簇首选择问题。文献[5]提出了一种改进的灰狼优化算法FIGWO来优化簇首选择，将适应度值作为猎物新位置权重，充分考虑节点当前状态最优解的最终位置，以合理选择簇首节点。文献[6]中首先使用SOM算法对网络进行分簇，然后在每个簇中使用改进的灰狼优化算法选择簇首。

上述协议在优化簇首选择、均衡网络能耗方面取得了一定的成效，但由于灰狼优化算法容易出现局部最优和精度不够等问题，导致选择的簇首不一定为最优，所以仍需进一步研究和改进。本文提出一种基于改进灰狼优化(grey wolf optimization，GWO)和差分进化(differential evolution，DE)的混合算法对WSN进行簇首选择(diffe-rential evolution and grey wolf optimization，DEGWO)。将差分进化算法混合到灰狼优化算法中，调整混合算法的收敛因子与缩放因子，避免了GWO早熟收敛而无法有效地搜索最优解的问题，从而选择最优的簇首。

1 系统模型

1.1 网络模型

对本文算法与对比算法所使用的网络模型，做出如下假设：

(1)所有节点和基站在部署后是静止的，每个节点分配一个索引。

(2)所有节点初始能量相同且能够报告其位置。

(3)所有节点以固定速率测量环境参数，能够根据到目标的距离调整其传输功率并定期向目标节点发送数据。

(4)所有节点可以独立地与基站通信，基站的位置已知，具有较高的计算能力且没有能量限制。

1.2 能量消耗模型

本文使用与文献[7]相同的能耗模型，在该模型中，根据发送电路与接收电路之间的距离来选择能量消耗模型，在距离d上传输lbit数据所消耗的能量如式(1)所示

(1)

其中，Eelec为传输1 bit数据所消耗的能量，d0为距离阈值，传输距离d小于d0时，采用自由空间衰减模型，Efs是其功率放大所需能量。传输距离d大于d0时，采用多径衰减模型，Emp是其功率放大所需能量。距离阈值d0如式(2)所示

(2)

节点接收和融合lbit数据消耗的能量分别如式(3)和式(4)所示

ERX(l)=lEelec

(3)

EDA(k)=lEda

(4)

其中，Eda表示节点融合1 bit数据所消耗的能量。

1.3 网络生存期模型

在大多数应用中，当某些节点出现故障时，网络仍能有效地运行。特别是当大量传感器节点部署在一个区域时，一个节点有几个相邻节点，这些邻居节点配备了相同的传感设备，所以网络将能够应对某些节点的故障。因此，第一个节点的死亡时间不是评估网络生存期的唯一指标[8,9]。在评估高节点密度的性能检测时，部分节点的死亡时间(a part of node die，PND)是一个更有效的指标[10]。将网络的生命周期描述如式(5)所示

(5)

其中，N是网络中传感器的数量。k是活动节点的数量。该式表明，PND的定义为活动节点与初始节点个数的比例下降到阈值ξ的时间。

2 基本算法

2.1 灰狼优化算法

在GWO[11]中，灰狼群体被分为α、β、δ、ω这4个社会等级[12]，其中，最优解为α狼，次优解为β狼，第三优解为δ狼，其余的解为ω狼，寻优过程是由α、β、δ狼领导ω狼更新位置，最终获得近似最优解。

GWO中，灰狼群体首先对猎物进行包围，灰狼包围猎物的数学模型的如式(6)和式(7)所示

D=|CXp(t)-X(t)|

(6)

X(t+1)=Xp(t)-AD

(7)

其中，t表示当前迭代次数，A和C表示系数向量，X为灰狼的位置，Xp为猎物的位置。D为猎物与灰狼的距离。A和C如式(8)和(9)所示

A=2a·r1-a

(8)

C=2r2

(9)

其中，r1、r2为在[0,1]取值中的随机向量，a为收敛因子，a如式(10)所示

(10)

其中，t是一个介于0到maxIter之间的整数，并且在迭代过程中每次增加1。maxIter为最大迭代次数。因此，a(t)在迭代过程中，从2到0线性递减。

包围猎物后，GWO执行狩猎过程以不断更新自己的位置，狩猎行为的数学模型如式(11)～式(13)所示

Dα=|C1Xα-X|
Dβ=|C2Xβ-X|
Dδ=|C3Xδ-X|

(11)

X1=Xα-A1Dα
X2=Xβ-A2Dβ
X3=Xδ-A3Dδ

(12)

(13)

2.2 差分进化算法

DE算法主要经过种群的初始化、变异、交叉、选择4个过程[13]。其各数学模型描述如下：

(1)初始化

(14)

其中，i=1，2，3，……，NP。n是总体向量的维度。NP是种群规模，上标G表示第G代。这些初始种群是在[0,1]之间的均匀分布随机选择的。

(2)变异

变异运算在基向量上加一个差分向量，变异运算DE/current-to-best/1如式(15)所示

(15)

(3)交叉

交叉运算是在待变异个体和变异后的新个体进行元素的交换。通过式(16)实现对目标向量和变异向量的交叉运算

(16)

其中，j=1，2，…，n，rand为[0,1]内一个随机的数。CR为交叉概率。jrand为[0,n]内随机选择的索引。

(4)选择

选择运算是在父代个体和子代个体中选择适应度值较高的保留到下一代。选择运算如式(17)所示

(17)

3 基于DEGWO算法的簇首选择

基于DEGWO的簇首选择算法使用经典分簇路由协议中“轮”的思想，将网络的每个运行轮次分为分簇阶段与数据传输阶段。分簇阶段，基站首先使用本文中所提均值法选出初始簇首集合，然后根据距离形成初始簇，在每个簇内，使用DEGWO算法选取出最终簇首。数据传输阶段，簇内节点通过TDMA的方式将数据发送给簇首，簇首节点将接收到的数据融合之后采用CDMA的方式发送给基站。

3.1 形成初始簇

在WSN中，簇首比普通节点消耗的能量多，所以，保证簇首在网络中均匀分布至关重要。基于DEGWO的簇首选择算法，首先采用均值法选取初始簇首，并且形成初始簇，然后在每个簇中使用DEGWO选择最终簇首，使用均值法选取初始簇首并形成初始簇的步骤如下：

步骤1 初始化(节点位置、能量等参数)。

步骤2 根据3.2.4节中适应度函数式(21)计算每个存活节点的适应度。

步骤3 对步骤2中计算出的适应度进行排序。

步骤4 将排序后的适应度均匀的分成K个集合。

步骤5 计算每个集合中的适应度值的平均值。

步骤6 计算每个集合中的每个节点与平均值的差值。

步骤7 与平均值差值最小的节点即选为初始簇首。

步骤8 普通节点选择加入最近的簇首，形成初始簇。

3.2 使用DEGWO选择最终簇首

3.2.1 DEGWO算法选择簇首

由于基本GWO在执行猎物攻击操作时容易陷入停滞状态[14]，使用基本GWO算法优化簇首选择并不能保证得到最优近似解。而DE具有强大的搜索能力，将DE混合到GWO中可以扩大种群搜索范围，避免种群迭代到达某一区域时出现局部极值。因此，本文提出一种基于DEGWO的簇首选择算法，在父代个体结束更新位置后，使用DE算法对GWO中个体进行交叉、变异、选择操作来维持种群的多样性，避免GWO陷入停滞状态，从而获得全局最优解。使用DEGWO选取最优簇首的步骤如下：

步骤1 初始化参数。

步骤2 将初始簇中个体初始化为灰狼父代种群，随机初始化变异种群、子代种群。

步骤3 根据3.2.4节中的适应度函数式(21)计算父代个体的适应度值。

步骤4 将步骤3中排名前三的个体分别设置为α、β、δ狼。

步骤5 使用3.2.2节中式(18)收敛因子a与式(6)～(13)对GWO中父代灰狼种群的位置进行更新。

步骤6 使用3.2.3节中缩放因子F与式(15)产生变异(中间体)种群。

步骤7 通过式(16)的交叉运算产生子代种群。

步骤8 依据式(17)判断是否更新父代种群。

步骤9 更新参数a、A、C。

步骤10 确定是否达到了最大的迭代次数，若是则停止返回猎物位置作为最优解，否则返回步骤3。

步骤11 得到最优位置，距离最优位置的节点即当选为簇首。

3.2.2 优化收敛因子

在GWO中，搜索新猎物与攻击猎物之间的过渡取决于收敛因子a和系数向量A，通过式(8)得出A的值为区间 [-2a，2a] 中的随机值。在 |A|>1时灰狼搜索新猎物，在 |A|<1时灰狼开始攻击猎物的行为。通常，在搜索空间的搜索越广，局部最优停滞的概率越低。为了获得更广的搜索空间，在迭代中调整式(8)中收敛因子a为非线性衰减，如式(18)所示

(18)

其中，iter为当前迭代次数，maxIter为最大迭代次数。

3.2.3 调整缩放因子

DE在搜索过程中式(15)中的缩放因子F取值一般为[0,2]之间的固定实数。但是，这样会导致一些问题，如果变异率过大，则算法的搜索效率较低，全局最优解的精度较低，变异率太小，种群多样性降低。因此，本文通过产生[0,2]之间的均匀分布的随机数做为缩放因子，以增加搜索到全局最优解的概率。

3.2.4 适应度函数设计

能量是节点最大的挑战，簇首节点的能量消耗比普通节点多。选择能量较高的节点作为簇首有助于平衡网络的能量消耗。因此，设计适应度函数中能量部分f1如式(19)所示

(19)

其中，E0表示节点的初始能量，Eres(i) 为节点的剩余能量。

传感器的能耗与传输距离成正比。传输距离越长，能耗越大。在选择簇首时，选择离基站更近的节点可以有效降低簇首的能耗。因此，设计距离影响因子f2如式(20)所示

(20)

其中，MaxD表示所有节点到基站最远的欧式距离，MinD为所有节点中到基站最近的欧式距离，D(i)为当前节点到基站的欧式距离。

综上所述，适应度值函数设计如式(21)所示

Fitness=uf1+(1-u)f2

(21)

其中，Fiteness为适应函数，u为权重系数。

3.3 数据传输

数据传输阶段，为防止簇内成员间的数据冲突，簇内数据通过时分多址(time division multiple address，TDMA)的方式进行传输，由簇首节点给簇内的各个节点分配通讯时隙，并以广播的形式通知簇内节点。所有节点均在自己的时段内完成数据传输，在其它时间进入休眠状态，以减少能耗。稳定数据传输阶段，节点在自己的数据传输时段内把所收集的数据发送给簇首节点后，由簇首节点对数据进行融合处理后以码分多址(code division multiple access，CDMA)的方式发送到基站。使用DEGWO算法选择簇首并进行数据传输的整体流程如图1所示。

图1 基于DEGWO算法的分簇路由流程

4 仿真结果与分析

4.1 仿真环境与实验参数

本文使用Matlab R2014b对本文所提算法DEGWO与LEACH、LEACH-E、FIGWO这3种协议进行仿真实验，并以网络生命周期中PND中的3个指标和网络总能量消耗为标准进行比较。为验证所提算法对多节点的适应性，设计了3种不同节点个数的网络场景进行实验，3种实验场景见表1。

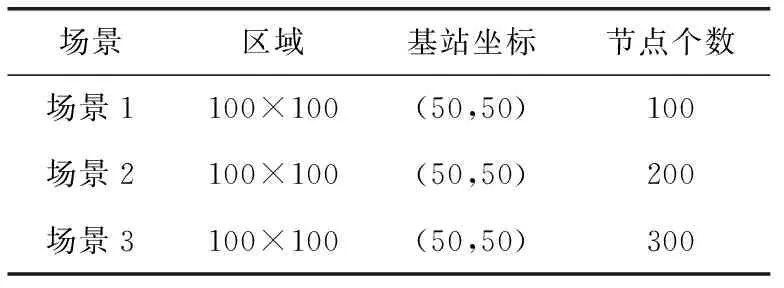
表1 3种网络场景

并按照文献[15]将最佳簇首个数设置为5%，DEGWO算法迭代次数为20次，种群大小为初始簇中节点的个数，适应度函数权重系数u为0.5，各仿真实验参数见表2。

表2 仿真实验参数

4.2 网络生命周期

网络生命周期是评价WSN能耗的重要指标之一，网络生命周期越长，验证能量消耗越均衡，网络对数据的吞吐量越大。场景1、场景2、场景3下以轮为单位模拟时间绘制的死亡节点数量如图2、图3、图4所示，从图2、图3、图4中可以看出，相较于其它3种协议，基于DEGWO的簇首选择算法在3种不同节点个数的场景下均能很好的将节点的生存时间延长。

图2 场景1下的生命周期对比

图3 场景2下的生命周期对比

图4 场景3下的生命周期对比

在节点密度方面，随着网络中节点数量的不断增加，网络结构变得复杂，合理的簇首选择对均衡整个网络的能耗的影响变得尤为突出。由于LEACH协议是根据阈值选取簇首，导致簇首的分布是随机的，这样虽然能保证每个节点成为簇首的可能性都是相等的，但是同时也导致了不合理的节点被选为簇首，加速了网络中节点的死亡速度。LEACH-E协议中虽然在LEACH的基础上将节点剩余能量的影响加入到簇首选择阈值中，这样可以使剩余能量较高的节点更容易被选为簇首节点，但是，其选择簇首时仍然采用随机的方式。导致LEACH-E协议相对于LEACH协议在延长网络的生命周期方面能有一定的提升效果，但是，随着节点数量的提升，提升效果变得越来越小。相对于LEACH协议与LEACH-E协议，FIGWO协议采用了改进灰狼优化算法优化簇首的选择，使选择的簇首变得相对合理，所以有一个较大的提升。但是，由于GWO存在容易陷入局部最优解的问题，导致其优化的簇首选择并不一定为最优。本文提出的基于DEGWO的簇首选择算法，能够根据网络的结构合理的对网络进行划分，针对GWO存在的缺点，使用DE算法对GWO进行变异、交叉操作，能够避免GWO陷入局部最优解，保证选择的簇首集合为全局最优。所以，相较于其它3种协议，本文所提的簇首选择算法DEGWO对网络生命周期方面有明显的延长效果。并且，随着节点数量的增加，仍然有一个明显的提升效果。

为了更直观对比网络生命周期，以PND中第一个节点的死亡时间FND(first node dead)、一半节点的死亡时间HND(half node dead)、最后一个节点的死亡时间LND(last node dead)作为网络生命周期的评估标准。场景1、场景2、场景3下FND、HND、LND的对比如图5、图6、图7所示。其中，FND、HND、LND具体数据见表3、表4、表5。

图5 场景1下的PND对比

图6 场景2下的PND对比

图7 场景3下的PND对比

从图5、图6和图7中可以看出，本文提出的DEGWO簇首选择算法在不同节点密度的3个场景下对WSN生命周期的各个阶段都有明显延长。从表3、表4和表5中可以得出，相较于LEACH协议、LEACH-E协议、FIGWO协议，基于DEGWO的簇首选择在第一个场景下将第一个节点的死亡时间延长了48.6%、16.6%、15.2%，将网络的整个生命周期LND延长了77.9%、53.7%、12.9%，在场景2下将第一个节点的死亡时间延长了37.7%、21.4%、10.9%，网络的整个生命周期LND延长了74.0%、44.9%、19.9%，场景3下，将第一个节点的死亡时间延长了33.0%、29.5%、5.8%，网络的整个生命周期LND延长了66.0%、48.7%、4.7%。可见，随着网络中节点数量的增加，本文提出的簇首选择算法在网络的各个时间点对网络的生命周期有较大程度的延长，这是由于DEGWO算法在网络中选择簇首时，使得最终的簇首集合在整个网络中是全局最优的。

表3 场景1下PND数据对比

表4 场景2下PND数据对比

表5 场景3下PND数据对比

4.3 网络剩余能量

网络剩余能量是WSN中所有存活节点的剩余能量之和。同一时间点下，网络的剩余能量越多，说明网络的能量消耗越均衡，能量利用率越高，网络的服务时间也会越长。3种场景下网络总剩余能量随时间的变化如图8、图9和图10所示，可以看出，本文提出的簇首选择算法DEGWO总的剩余能量在各个时间点都高于其它3种协议。例如，在整个网络运行到1000轮时，在场景1下，LEACH协议总的剩余能量百分比为9.87%，LEACH-E为23.62%，FIGWO为41.28%，而DEGWO为45.51%。在场景2下，LEACH协议总的剩余能量百分比为14.24%，LEACH-E为18.89%，FIGWO为37.01%，而DEGWO为46.22%，场景3下LEACH协议总的剩余能量百分比为15.44%，LEACH-E为18.68%，FIGWO为41.77%，而DEGWO为46.17%。可见，随着网络节点数量的增加，LEACH协议与LEACH-E协议之间总剩余能量的差距变得越来越小，虽然LEACH-E协议是在LEACH协议之上改进，但随着网络节点数量的增加，提升效果变得越来越差，可以得出，相较于LEACH协议，LEACH-E协议在大规模节点的情况下，在均衡能量消耗方面，并不能有一个很好提升的效果。相较于LEACH协议与LEACH-E协议，本文所提簇首选择算法DEGWO与FIGWO协议使选择的簇首更加合理，能更好均衡网络中的能量消耗。从图8、图9、图10中可以看出，相较于FIGWO协议，本文所提簇首算法表现更优，并且随着网络节点数量的增加，均衡能耗的效果并没有降低，反而有一个阶段性的提升，可见，本文簇首选择算法DEGWO在网络节点数量增加时，均衡全局能量消耗的适应性更好。

图8 场景1下的总剩余能量对比

图9 场景2下的总剩余能量对比

图10 场景3下的总剩余能量对比

5 结束语

针对无线传感器网络中节点的能量消耗不均衡、网络生存期短的问题，本文提出了一种基于DEGWO的簇首选择算法，将差分进化算法与灰狼优化算法混合，调整混合算法中的收敛因子与缩放因子，改善了灰狼算法易陷入停滞的缺点；随后通过节点的剩余能量和节点与基站的距离设计适应度函数，用于选择网络中最适合的节点作为簇首节点。仿真实验结果表明，与LEACH、LEACH-E和FIGWO相比，本文提出的簇首选择算法DEGWO能显著延长网络的生命周期、均衡网络的能耗。下一步的研究中将对网络中节点的路由方式进行研究，设计多跳路由，能更好优化网络的能耗、延长网络的生存期。