基于Eband算法的运动控制平滑性优化

王素芳，安传旭，蒋文婷，杨 林，王浩枫

(1.中国航天科工集团第二研究院 七〇六所，北京 100854；2.中国科学院 软件研究所，北京 100190；3.中国空间技术研究院 通信与导航卫星总体部，北京 100094)

0 引 言

ROS自主移动机器人[1]需要解决定位、导航、规划、控制等问题，导航是其核心技术，导航主要基于ROS的move_base框架来实现，导航[2-4]就是让机器人可以自主按照内部预定的信息，或依据传感器获取外部环境进行相应的引导，从而规划出一条适合机器人行走的路径。因此，导航成功的关键在于路径规划[5,6]，路径规划由全局路径规划和局部路径规划[7]组成。全局路径规划使用路径规划算法，在二维栅格地图中规划出一条可行路径，而局部路径规划则是在全局路径的基础上做出动态的规划和运动控制，以达到实时避障的效果[8,9]。

常见的局部路径规划器有DWA(dynamic window approach)[10]动态窗口法、TEB(timed elastic Band)[11]时间弹性带、pure pursuit跟踪算法[12]、MPC(model predictive control)[13]模型预测控制和Eband[14]等。TEB[15,16]是起始点、目标点状态由用户/全局规划器指定，中间插入N个橡皮筋形状的控制点(机器人姿态)，为了显示轨迹的运动学信息，在点与点之间定义运动时间Time，即为TEB算法，TEB[17]可以做到对前方一段轨迹进行优化，对动态障碍物的避障效果较好，但TEB算法计算复杂度较高，在控制过程中速度和角度波动较大。Eband[18]是一种类似于人工势场形成引力与斥力的方法生成弹性带(elastic band)进行局部规划，以提高机器人行走的速度与动作的连贯性。

针对规划器缺少对机器人运动的考虑，以及在遇到动态障碍物时，即使全局规划器可以重新规划路径，但也会出现当前位置偏离规划出的路径的情况[19,20]。本文采用Eband局部路径规划器来实现动态避障，使用Eband算法来优化前面所规划出来的路径，但其运动控制随着“气泡”的波动变化，导致路径有时不够平滑，因此，本文主要针对Eband的运动控制平滑性和机器人运动卡顿等急需解决的关键问题，进行算法优化，并通过代码实现，将优化后的算法与原Eband算法进行对比，验证了本文方法的有效性。

1 Eband算法实现原理

Eband算法输入为全局的路径、局部costmap、机器人当前位姿；输出为控制速度(角速度与线速度)。Eband 采用气泡表示，每个气泡均处在free space里面，并且每个气泡与相邻的2个气泡重叠。每个气泡的半径是机器人与障碍物的最短距离，气泡通过计算合力(相邻的点产生的引力与障碍物产生的斥力)决定其位置。通过下一个气泡的中心位置，计算得出控制的线速度与角速度。

气泡“bubble”就是一个代表机器人路径上的点与障碍物不碰撞的圆形区域，距离障碍物近时，气泡小，距离障碍物远时，气泡就会随之变大。定义气泡函数B(b)

(1)

其中，b表示当前气泡的中心，q表示当前气泡中的任意随机位置，ρ(b) 表示气泡以b为圆心的圆的半径。

具体流程如图1所示。

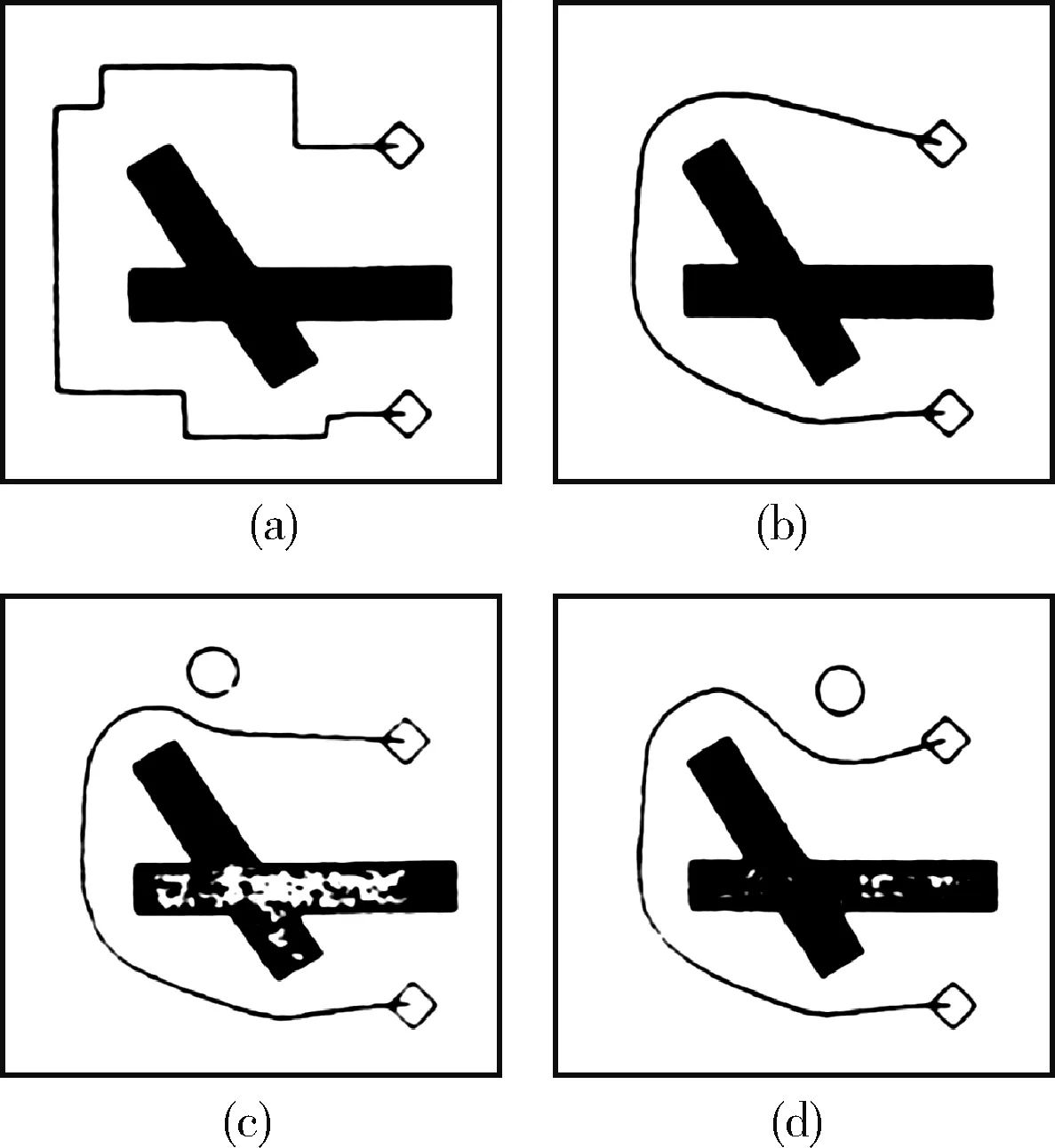
图1 路径规划

图1(a)为机器人全局路径规划器规划的路径，图1(b)为使用Eband局部路径规划算法之后的路径。为了改善路径的形状，主要有两个力，一个是收紧的力，一个是障碍物产生的斥力，直到二力平衡，让原本松弛的路径看上去紧绷起来。图1(c)和图1(d)是通过Eband局部路径规划器规划后的路径随着机器人运动而根据环境中障碍物做出相应调整后的路径。

之后就是对产生的气泡做处理，比如将气泡前移或后移，使其在距离障碍物近的地方生成的气泡密集,在距离障碍物远的地方生成的气泡稀疏。气泡沿着路径产生和随着障碍物改变情况如图2所示。

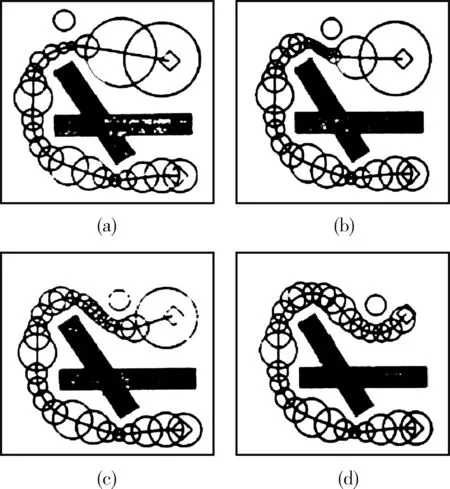
图2 气泡沿着路径产生和随着障碍物改变情况

如图2所示，空心圆表示障碍物，障碍物靠近导致附近的气泡变小变密，障碍物远离后，气泡变大变稀疏。但是在机器人附近突然出现障碍物时，气泡会出现跳变的现象；或者机器人在有垃圾桶、消防栓、杂物等障碍物的狭窄走廊里移动时，以及在狭窄的路段突然转弯时，气泡会变小，气泡太小就可能存在band断裂，此时机器人会重新规划路径和插值，局部路径目标点就会发生变化，就会引起机器人运动卡顿。

2 改进的Eband算法

针对Eband气泡在特定场景下的跳变，会直接导致局部路径当前目标点的跳动，以及运动控制速度的波动，从而导致机器人运动卡顿不平滑问题。为了解决该问题，本文主要从曲率算法优化、速度乘积因子去噪和速度插值3个方面进行了优化。

2.1 曲率算法优化

针对突然出现的障碍物引起气泡半径的瞬间变化，导致运动曲率骤变问题，做了曲率计算优化，平滑大幅度的曲率变动引起机器人线速度的骤减。

在生成的局部路径上，截取3个气泡，分别是band[0]，band[1]，band[2]，band[0] 代表的是机器人的位姿，后续两个气泡代表机器人后续的两个位姿。那么band[0]，band[1] 和band[2] 就对应pose[0]，pose[1] 和pose[2]。 利用每个pose中的x,y坐标，就可以求出前后两个pose之间的角度变化。

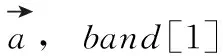
(2)

其中

x1=pose[1].pose.position.x-pose[0].pose.position.x
y1=pose[1].pose.position.y-pose[0].pose.position.y
x2=pose[2].pose.position.x-pose[1].pose.position.x
y2=pose[2].pose.position.y-pose[1].pose.position.y

本文用向量的夹角余弦值作为自身的曲率

(3)

将式(3)展开式即得到式(4)

(4)

2.2 速度乘积因子去噪

针对狭窄路段，Eband速度乘积因子出现噪点，引起机器人运动卡顿问题，做了狭窄路段速度乘积因子线性去噪。

速度乘积的影响主要取决于环境的狭窄度，当环境过于狭窄时，Eband的对应气泡半径就会急速减少，这时候线速度也应该对应减速，保障安全。算法输出线速度公式为

Max_vel_lin=max_vel_lin_*curvature_factor*
velocity_multiplier

(5)

式中：max_vel_lin_是曲率因子，表示转弯弧度对线速度的影响，velocity_multiplier表示空间狭窄度、气泡半径大小对线速度的影响

Scale=4-1.2/max_vel_lin_

(6)

式中：Scale表示环境的影响因子权重，当最大速度设置的越大时，环境的影响因子权重也就越大，该参数的选取主要是根据机器人的应用场景来决定，本文以最大线速度max_vel_lin_的取值范围 [0.3,1] 为依据，为了约束Scale的取值范围在 [0,2.8]， 设置了线性方程(6)，保证在速度很低的时候，Scale的影响为0，随着速度的提高，环境因子的制约逐步扩大，最多扩大到3，以适应机器人的应用场景

Offset=0.42/(max_vel_lin_-0.4)

(7)

式中：Offset表示为了平衡整个速度乘积，限制速度乘积的值域，用来控制最大最小速度范围，由于最大线速度的取值范围在 [0.3,1]， 为了在速度最低时候，速度乘积影响达到最大，满足值域 [0.02,1]， 选取了式(7)中的Offset的线性参数；

速度乘积的计算公式为

Velocity_multiplier=Scale*bubble_radius+Offset

(8)

从式(8)可以看到，速度乘积Velocity_multiplier由Scale和气泡半径bubble_radius以及Offset来决定，气泡半径最小的时候，Velocity_multiplier达到最小，表示周围环境比较复杂；反之气泡半径最大的时候，表示周围环境比较空旷安全，速度乘积达到最大；该因子的值域是 [0.4285,1]。

2.3 速度插值法

针对气泡的跳变导致的局部路径目标点跳变问题，本文进行气泡插值来规避跳变，为了机器人可以更平滑的输出到达局部目标点的速度，同时兼顾机器人避开障碍物的反应灵敏度，根据机器人的电机反应能力，选取机器人前方0.2 m距离处作为插值气泡中心，此值根据不同电机的性能做不同的选取，一般的范围在 [0.1,0.3]。 根据此处在band上前后气泡的半径，算出插值气泡半径。插值后的气泡作为局部路径目标点进行迭代更新。代码如下：

算法1：Interpolate and update bands

输入：planned path: plan=(bubble0,bubble1…bubblen).

输出：The target point for output: goal

(1)While (goal==empty) do

(2) band=convert(plan); //Plan is converted to band

(3) bubble_center=FindCenter (0.2, band); //Find the bubble center at 0.2 m

(4) r=FindMinDisBubble (band); //The nearest bubble radius is the radius

(5) InsertBubble (r, bubble_center, band); //Insert the bubble into the band

(6) SetLocalGoal (bubble_center); //Set the center of the bubble as the local goal

(7) PublishGoal (goal); // Publish new goal

(8)return goal;

(9)End.

3 实验分析

3.1 实验数据集

本文对比实验验证所用数据集为在同一场景下包含回形走廊、若干固定障碍物所录制的bag，订阅了/cmd_vel话题以及/vel_data话题，地图大小为20 m*20 m。并且保证录制环境中除了回形走廊、若干障碍物以外，其它影响因素可以忽略不计。

3.2 实验软硬件配置

本文优化后的算法与原Eband算法均在录制的同一数据集上进行实验验证。软件环境为：Ubuntu18.04+ROS melodic。硬件环境使用Firefly-RK3399Pro开发板进行代码部署，硬件部署环境如图3所示。

图3 Firefly-RK3399Pro开发板

在进行路径规划实验时，硬件环境采用国产高性能AI处理芯片RK3399Pro，集成神经网络处理器NPU，算力高达3.0 Tops，兼容多种AI框架。此芯片采用了ARM双核Cortex-A72+四核Cortex-A53的大小核处理器架构，主频高达1.8 GHz，集成四核ARM高端GPU Mali-T860 MP4图形处理器，通用运算性能强悍，整体性能优异。

ROS是一个开源的机器人操作系统软件框架。它提供了包括硬件抽象、常用功能的实现、进程之间的包管理、低级设备控制和消息传递等希望从操作系统获得的服务。它还提供了各种工具和库来编写和运行代码。

ROS的主要特点是：①分布式架构，ROS通过节点(Nodes)进行点对点的设计，可执行文件可以单独运行；②多语言支持，ROS是一个语言中立性的软件框架，支持C++、Python和LISP等多种不同的语言；③工具包丰富，诸如可视化和调试工具、仿真环境等是ROS中最为常用也最为重要的几个工具；④免费开源。

基于ROS的上述特点，在ROS中实现机器人路径规划是非常方便的，ROS还可以解决传感器驱动、显示和算法之间的沟通协调问题，而Ubuntu是Linux系统的一个发行版本，具有强大的防御病毒功能并且免费，因此本文所涉及到的算法均在Ubuntu18.04+ROS melodic机器人操作系统下编程实现，代码使用C++语言进行编写。实验对比图使用ROS自带的rqt-plot绘图工具进行数据曲线比较。

3.3 实验数据对比

3.3.1 平滑曲率算法优化

本节实验中优化了曲率限制对于速度的抑制效果突兀问题，对比不同曲率范围时速度下降的效果，其中d为前后曲率的变化data。参数介绍如下：

当d<1.0时，如图4所示。

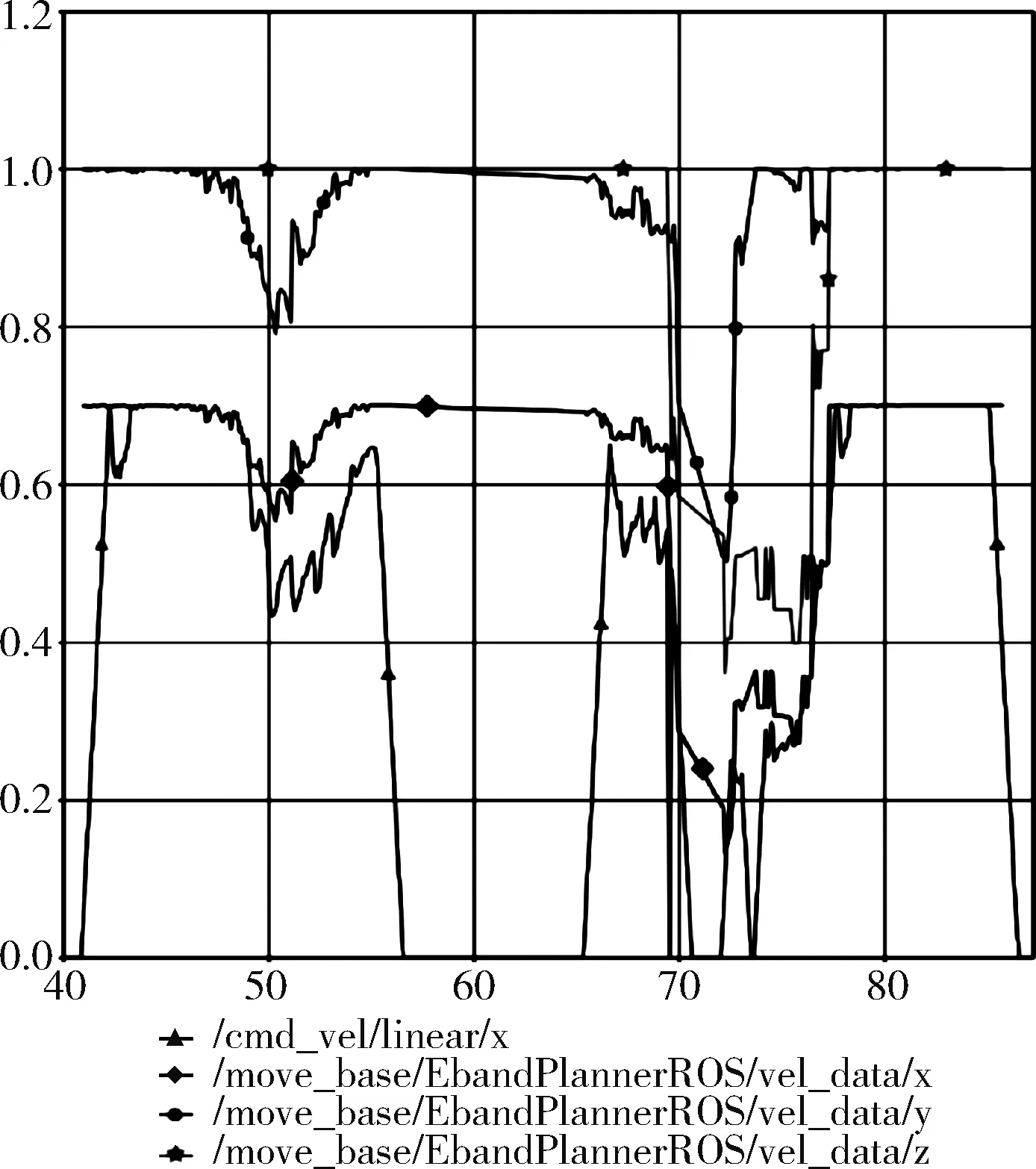
图4 d<1.0时曲率对各参数的影响曲线

由图4可以看出，当d<1.0时，可见曲率因子的变化，会引起线速度的剧烈变化，对原算法输出的线速度的影响效果较为明显。

当d<0.2时，如图5所示。

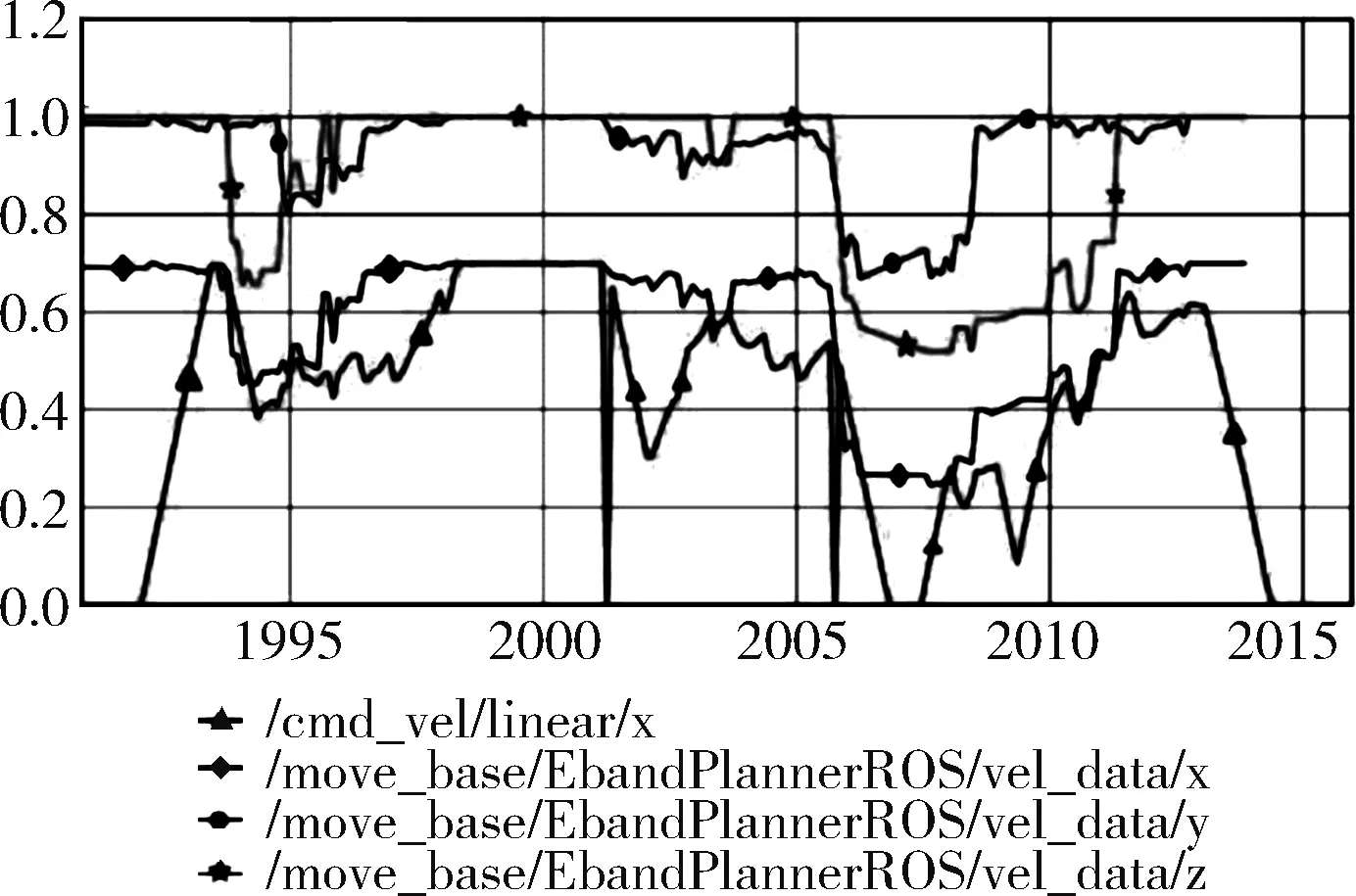
图5 d<0.2时曲率对各参数的影响曲线

由图5可以看出，当d<0.2时，有效限制了曲率因子的断崖式变化。

当d<0.1时，如图6所示。

图6 d<0.1时曲率对各参数的影响曲线

由图6可以看出，曲率因子的波动基本稳定，但是对原算法输出的线速度的影响效果也越来越小，影响最大的因子变成了速度乘积因子。

当d<0.15时，如图7所示。

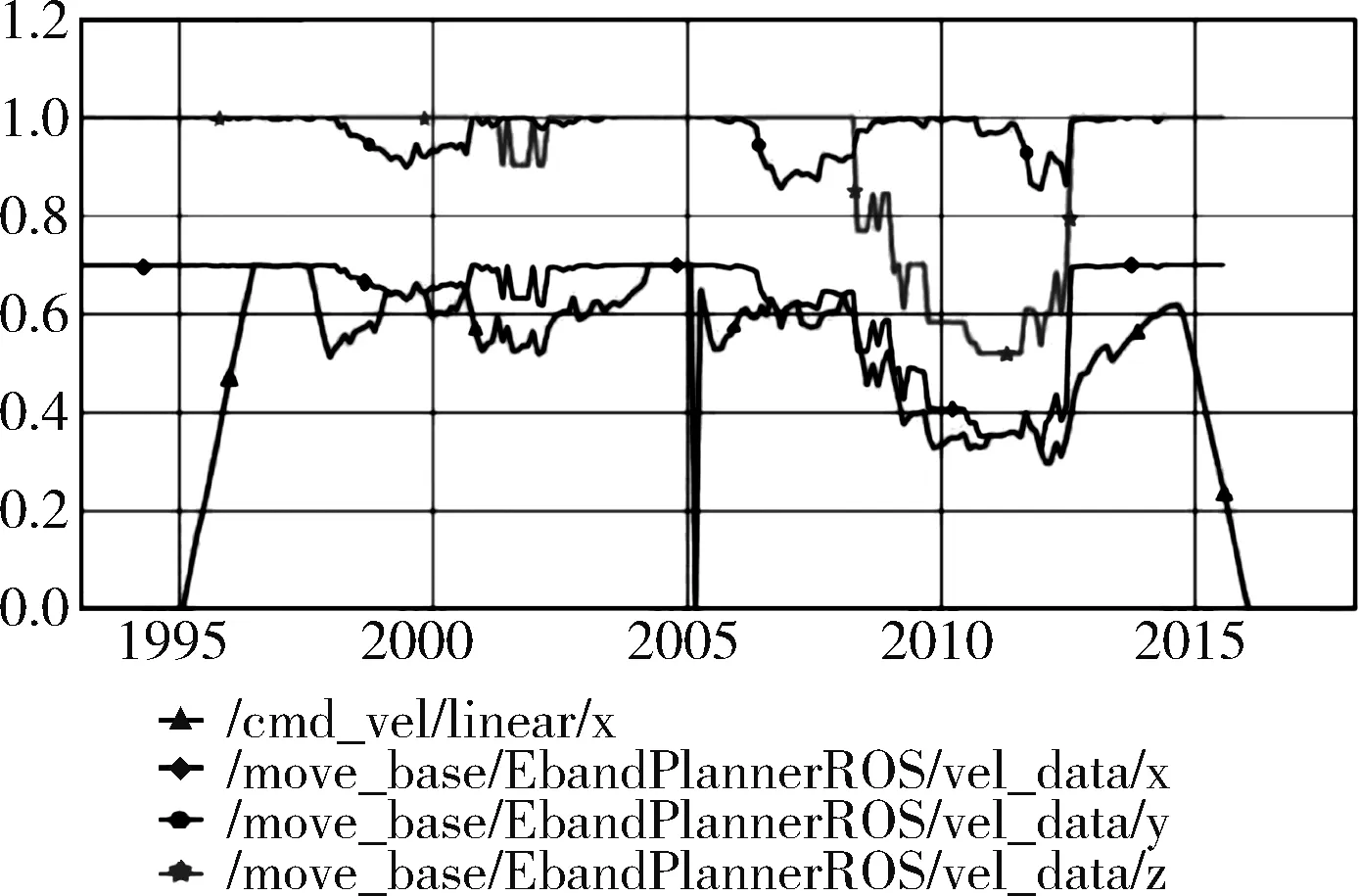
图7 d<0.15时曲率对各参数的影响曲线

由图7可以看出，机器人运动底盘里程计线速度和算法输出的最大线速度曲线基本拟合，此时，曲率因子的影响效果达到比较优秀的效果。

平滑曲率前后的整体效果曲线对比，如图8和图9所示。

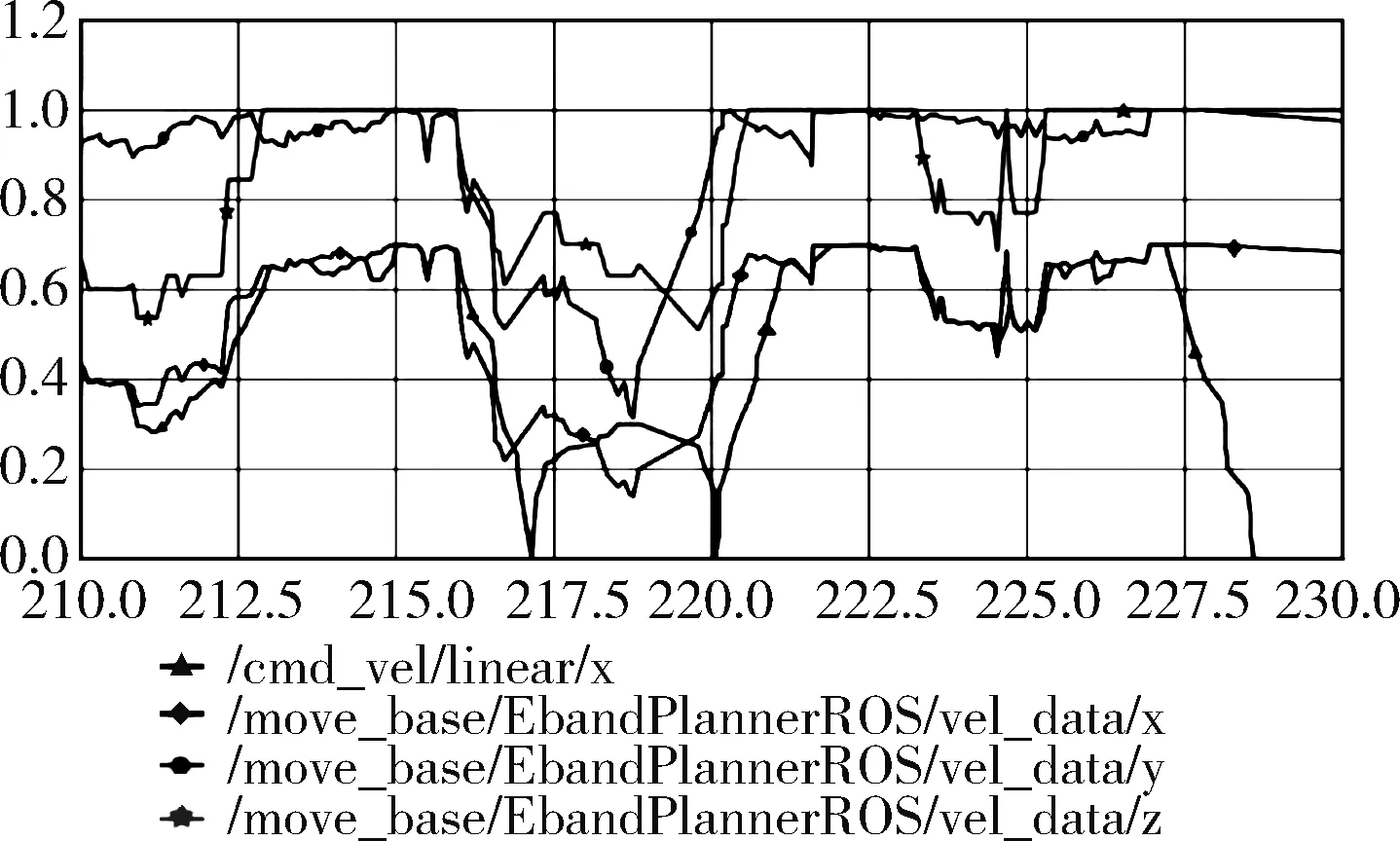
图8 平滑曲率前整体效果曲线

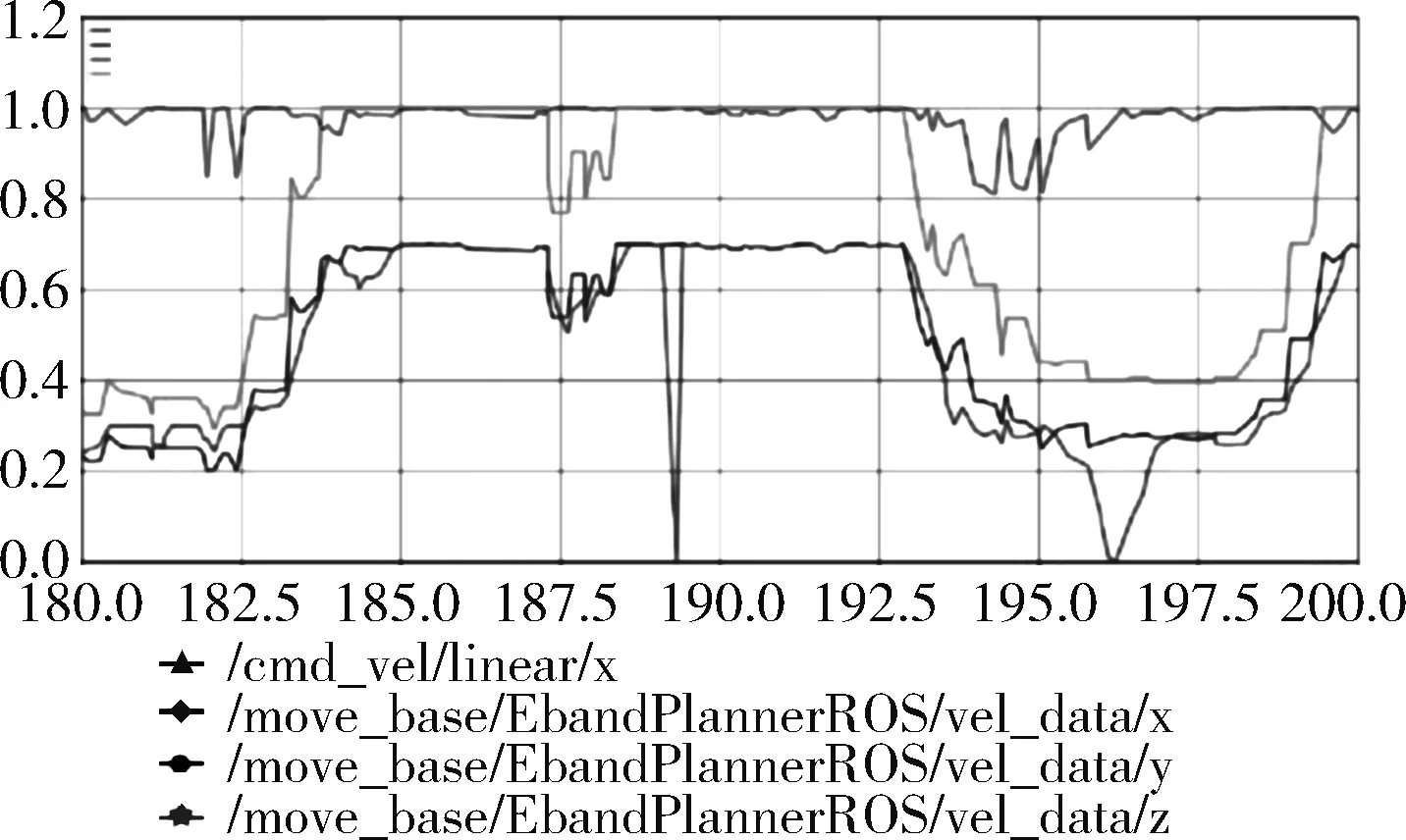
图9 平滑曲率后整体效果曲线

由图8和图9可以看出，针对突然出现的障碍物引起气泡半径的瞬间变化，导致运动曲率骤变的问题，由于曲率影响着转弯时候的最大线速度，本文算法对曲率参数的变化梯度做了优化，使得在突然出现障碍物和在障碍物周围转弯时的线速度更加的平滑，有效地抑制了大幅度的曲率变动引起机器人线速度骤减的情况发生。

3.3.2 速度乘积因子去噪

当在机器人在狭窄空间内运动，由于环境本身比较狭窄，Eband生成的气泡半径可能很少达到最大，机器人此时的线速度受到了速度乘积因子的直接影响。在此场景下，若突然出现静态或动态的障碍物，band对应的气泡半径存在小于0.1 m的可能，而在Eband的速度设置中，气泡半径小于0.1的时候线速度已经相当微小，而真实场景中机器人又需要继续缓慢平稳向前，要实现这一目标，气泡半径小于0.1 m时速度因子的影响对于线速度而言就成为了噪点，本实验对此问题进行了去噪工作：

优化前如图10所示。

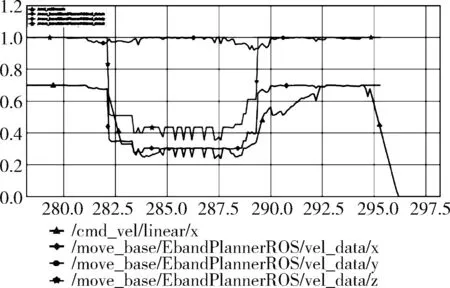
图10 速度乘积因子去噪前各参数曲线

观察图10，本实验设置了线速度的最小值为0.3 m/s，但是由于噪点存在，算法输出的线速度出现了很多低于0.3的极值点，这些极值点是速度乘积瞬间值造成的，是无效不可用的点，对线速度的平滑性也有直接影响，需要进行优化去噪。

优化后如图11所示。

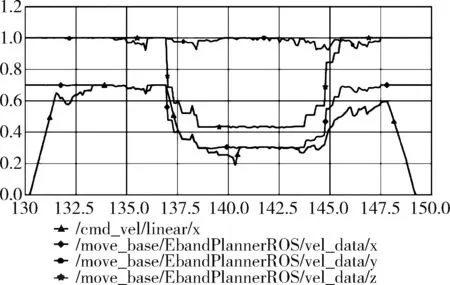
图11 速度乘积因子去噪后各参数曲线

观察图11，可以看到算法输出的线速度已经没有低于0.3的极值点，噪点被去除。速度乘积主要影响着机器人经过狭窄空间时的运动，限制速度乘积在短时间气泡很小的时候的影响力，减少由此造成的线速度波动，使得机器人在狭窄空间运动的时候，速度更加平滑。

3.3.3 局部目标点插值

经过曲率和速度乘积的优化后，Eband算法输出的线速度已经比较平稳。Eband在局部路径规划和控制中，采取了分段控制的策略。首先得到全局路径规划的曲线后，先由设置的局部代价地图大小，截取相应长度的全局点作为局部路径目标点，然后由算法生成气泡连成的band，该band可以转化成path，也即是局部路径。然后交给速度控制，速度控制以机器人最近的气泡中心作为临时目标点，进行短距离的运动，这也是Eband可以快速应对突发障碍物的原因之一。

但是此种方式也存在一定的弊端，首先机器人在不断的运动中，局部路径规划器也在不停的规划，面对动态的障碍物时，算法生成的气泡和路径都在动态更新，这就意味着局部临时目标点可能会发生改变。局部临时气泡中心的跳变直接影响到角速度和线速度的控制，也就造成了一定的震荡和卡顿，观察图12，可以看出算法输出线速度的曲折和不稳定。

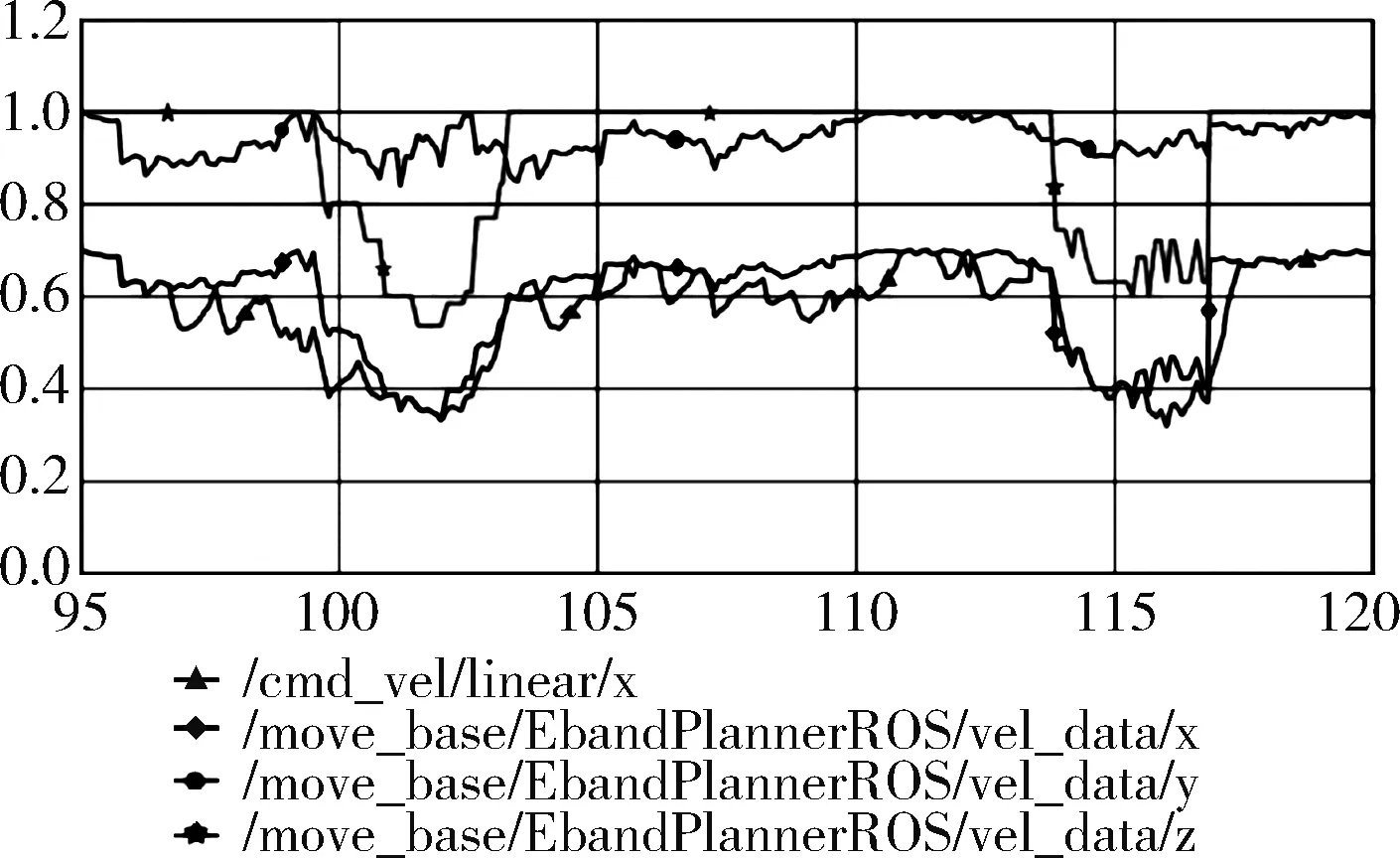
图12 局部目标点插值前各参数曲线

既然局部临时目标气泡中心可能发生跳变，我们可否设置一个在band中不会发生剧烈跳变的气泡中心作为临时目标点呢？答案是可行的。为了实时性的不受影响，我们在距离机器人较近的band中进行气泡插值，气泡中心的选定为距离机器人0.2 m处，气泡半径由该处前后两个气泡半径共同影响。这样气泡中心的位置就变成了相对稳定的值。观察图13。

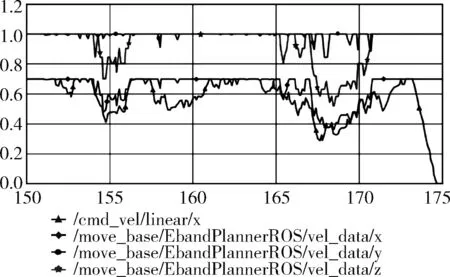
图13 局部目标点插值后各参数曲线

观察算法输出线速度曲线，算法输出的线速度相比图10平滑性有了大幅度提升，相对的里程计输出线速度也随之趋向平稳。局部目标点插值可视化效果如图14所示。

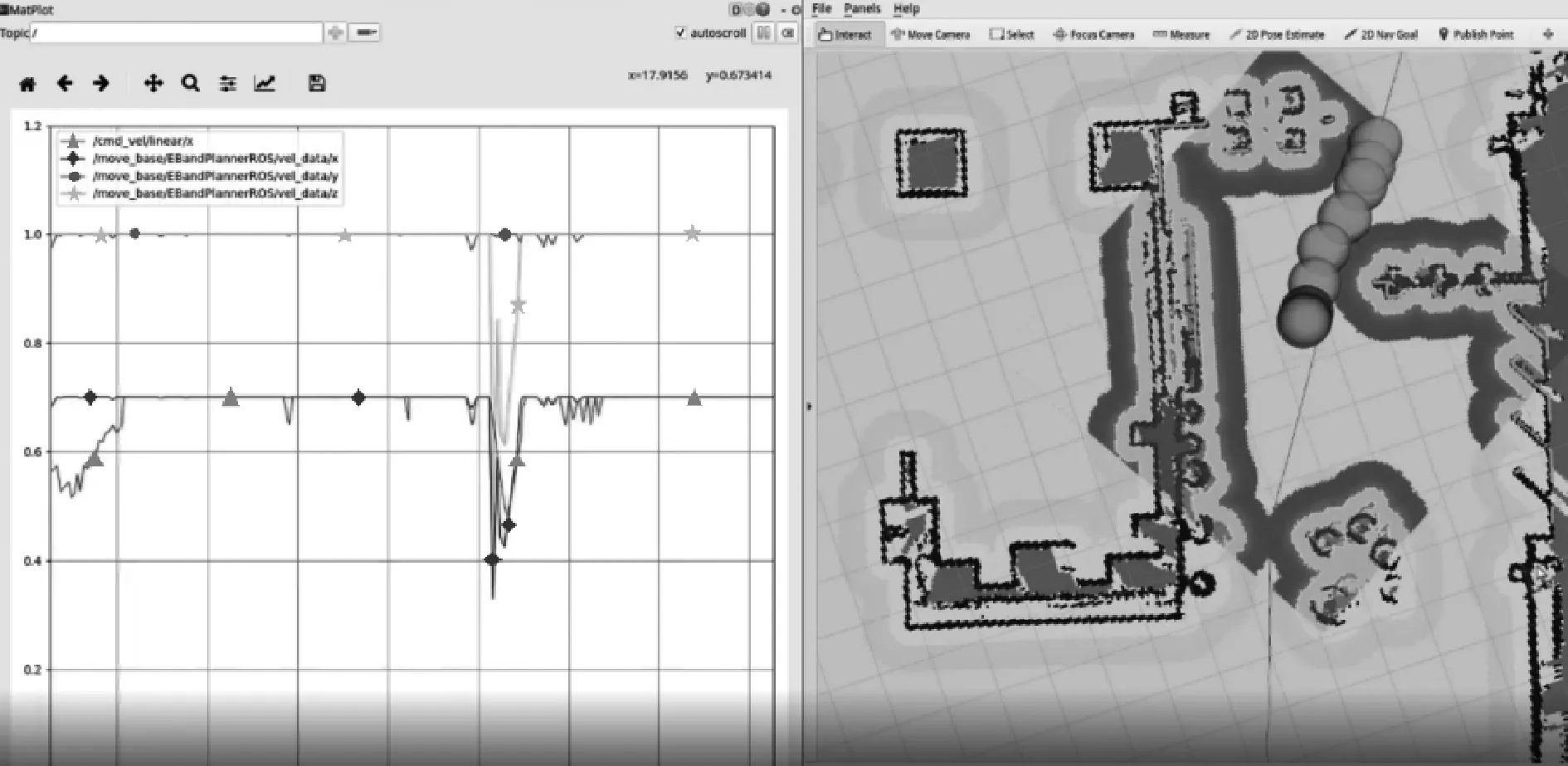
图14 局部目标点插值可视化效果

其中从下向上数第二个气泡为局部目标插值点，也可称之为速度插值点，气泡连成的band即为局部路径规划器实时规划的局部路径，对比左侧速度控制输出，可以看到机器人在以相对平滑的线速度平稳运动，算法发布的线速度和里程计发布的速度拟合程度也更高。

4 结束语

针对Eband算法存在的气泡突变、曲率对线速度影响较大以及机器人运动卡顿问题，主要进行了以下3方面工作：

(1)曲率因子的平滑有效缓解了曲率因子对线速度的过度抑制，更换了曲率因子的计算方式，使得其对于线速度的影响更加合理；

(2)速度乘积因子的去噪，在一定程度上减轻了机器人运动控制的卡顿感觉，在狭窄空间内机器人运动会更加平滑；

(3)局部目标点插值，有效解决了由于气泡的跳变引起的局部目标点跳变和速度控制变化问题；

局部路径和全局路径规划方法仍然存在很多不足之处，需进一步研究改进，除此之外，局部路径规划和全局路径规划协同工作，机器人才可以更好地规划出从起点到终点的运动路径。