改进蝴蝶算法优化支持向量机的土壤含水量预测模型

王仲英，刘秋菊

(1.河南省智慧农业远程环境监测控制工程技术研究中心 应用技术研究院，河南 郑州 450018； 2.郑州工程技术学院 信息工程学院，河南 郑州 450000)

0 引 言

常规土壤含水量预测法包括：经验法、烘焙法、电容法、时域反映法、水量平衡法、时序法、回归分析法以及神经网络预测法和支持向量机SVM预测法。经验法完全依赖人为主观意识测定，准确性较差。烘焙法、电容法、时域反映法、水量平衡法、时序法则与具体物理参量相关，通用性、稳定性比较受限。如：文献[1]利用经验模型测定土壤含水量与其贮水量的关系，文献[2]利用水量平衡模型对土壤含水量进行预测，模型精度有一定提升。水量平衡法所需要测量数据太多，计算代价过高，且复杂。文献[3]利用时序法预测土壤含水量，并结合回归预测实现了较好的预测效果。文献[4]结合偏最小二乘回归模型和主成分分析法研究气象因子与土壤含水量的预报模型，预报精度有所提升。文献[5]利用灰色理论与BP神经网络的结合，测量各数据特征与土壤含水量的关联性，在残差分析和关联度检验上验证了预测准度。文献[6]利用BP神经网络进行土壤含水量预测，通过学习速率自适应调整提高预测精度。文献[7]为了提高BP神经网络的预测精度，先利用改进樽海鞘算法对网络结构优化，再利用BP神经网络进行土壤含水量预测，训练时间能够有效缩短。文献[8]利用改进灰狼优化算法对神经网络进行改进，并建立土壤墒情预测系统，与标准神经网络预测相比，相对误差下降了4%。由于BP神经网络在收敛精度、泛化能力存在不足，导致该方法依然易于陷入局部最优。SVM则需要对相关参数和核函数选取做出优化，才可进一步提升预测精度。

蝴蝶优化算法BOA[9]是一种新型群体智能优化算法，其原理简单，依赖参数少，在寻优精度和收敛效率上已超过粒子群优化PSO、差分进化DE、蜂群优化ABC及引力搜索GSA算法等。然而，基本BOA算法依然存在寻优精度低、收敛速度慢的不足，其寻优稳定性、跳离局部最优能力依然还具有很大的改进空间。为了进一步提升BOA算法的寻优性能，本文将设计一种改进蝴蝶优化算法LGBOA，利用Levy飞行和高斯变异、混沌Logistic映射个体扰动机制，改进算法的寻优能力，并利用LGBOA算法对SVM模型的惩罚因子C和核函数参数γ寻优，构建土壤含水量预测模型LGBOA-SVM。结果验证LGBOA-SVM可以有效提高土壤含水量预测精度和效率。

1 蝴蝶优化算法BOA

蝴蝶飞行过程中，会产生一种香味并在空气中扩散，其它蝴蝶可以闻到该香味，并根据香味浓度被其吸引。当一只蝴蝶嗅到最佳香味时，会向其靠近，该过程称为全局搜索过程。而当个体无法嗅到任何蝴蝶香味时，该个体将在搜索空间内随机选取移动位置，该过程称为局部搜索。

蝴蝶飞行过程中会散发一种香味，香味浓度公式为

f=cIa

(1)

式中：I为刺激强度，c为感知形态，a为激励指数。

蝴蝶的运动模式分为两个阶段：

(1)全局搜索阶段：每只蝴蝶会在飞行过程中散发香味，其它蝴蝶会根据嗅到的香味浓度寻找目标。该模型定义为

(2)

其中，xi(t)为迭代t时蝴蝶个体i位置，g*为全局最优解，r1为[0,1]间的随机量，fi为蝴蝶个体i的香味浓度。

(2)局部搜索阶段：若蝴蝶个体无法感知其它蝴蝶的香味，它将在搜索空间内随机移动。该模型定义为

(3)

其中，xj(t)、xk(t) 为随机选择的个体，r2为[0,1]间随机量。

BOA算法进行全局搜索或局部搜索由概率阈值P决定，算法每次迭代中会生成随机数r3，并与P比较，具体模型为

(4)

2 LGBOA-融合Levy飞行与高斯混沌变异的BOA算法

2.1 基于Levy飞行的局部搜索位置更新机制

由式(3)可知，蝴蝶个体在进行局部搜索时，其移动步长主要由随机参数r2决定。随机变量尽管具有很好的等概率随机性，但搜索行为盲目，效率较低。为此，LGBOA算法引入Levy飞行策略改进BOA算法的位置更新方式。Levy飞行具备高频率的短步长搜索和低频率的长步长搜索模型，可以有效实现未知区域的随机搜索。

作为一种随机游走策略，Levy飞行结合了高频短步长的跳跃式搜索和低频长步长的行走策略，不仅可以有效地进行局部范围内的精细搜索，还可以确定一定比例的远距离区域内的有效勘探。Levy飞行服从Levy分布，定义为

Levy～u=t-λ, 1<λ≤3

(5)

Levy飞行是一种拥有重尾翼的概率分布。具体计算搜索路径的莱维因子Levy(λ)时，通常利用Mantegna的模拟Levy飞行路径公式，具体为

s=μ/|v|1/β

(6)

式中：0<β<2，通常取值1.5，μ、v服从正态分布

(7)

(8)

且

(9)

σv=1

(10)

得到Levy飞行路径Levy(λ)后，通过Levy(λ)取代BOA算法中局部搜索时个体位置更新的随机值r2，即可得到改进位置更新公式

xi(t+1)=xi(t)+(Levy(λ)2×xj(t)-xk(t))×f,
r3>P

(11)

2.2 基于高斯和混沌变异的个体扰动机制

式(2)表明，种群的全局搜索主要由当前最优个体g*引领，该方式可以充分发挥精英个体的导向作用。然而，处理多峰函数优化问题时，精英个体若已成为局部最优解，则会导致后期搜索因缺乏多样性而陷入早熟收敛。为此，LGBOA算法利用混合高斯和混沌变异机制对最优解g*进行扰动，以此扩展搜索空间，避免局部最优。

首先，引入一种早熟收敛、局部最优的判定方法[12]。令迭代t时的种群个体适应度方差SD(t)为

(12)

式中：N为种群规模，fi(t)为迭代t时个体i的适应度，由测试中的目标函数计算，favg(t)为迭代t时整个种群的平均适应度，fμ(t)为方差SD(t)的限定参数，定义为

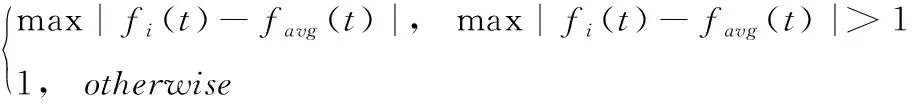
(13)

迭代t时种群个体的平均间距dis(t)定义为

(14)

式中：L为种群在搜索区域中的最大对角步长，dim为空间维度，xi,d(t) 为迭代t时个体i的d维位置，xavg(t) 为迭代t时d维位置的均值。

种群搜索趋于收敛时，种群位置趋于集中，此时适应度方差SD(t)和个体间距dis(t)逐步趋近于0。为了区分早熟收敛和全局收敛，定义SD(t)<10-5且dis(t)<10-2时，算法为局部收敛状态。

若判定为局部收敛状态，则精英个体的变异方式为

(15)

式中：δ为高斯变异算子， [lmin,umax] 为种群个体的搜索范围，r4为(0,1)内的随机值，φ为Logistic混沌值，定义为

φ(t+1)=c×φ(t)×(1-φ(t))

(16)

式中：c为混沌参数，c=4。

高斯变异算子服从以下高斯分布

(17)

式中：σ2为对应每个候选解的方差，φ为Logistic混沌值。通过该式，可以生成均值为0，标准差为1，服从高斯分布的随机量。

2.3 LGBOA算法流程和时间复杂度分析

LGBOA算法流程如图1所示。

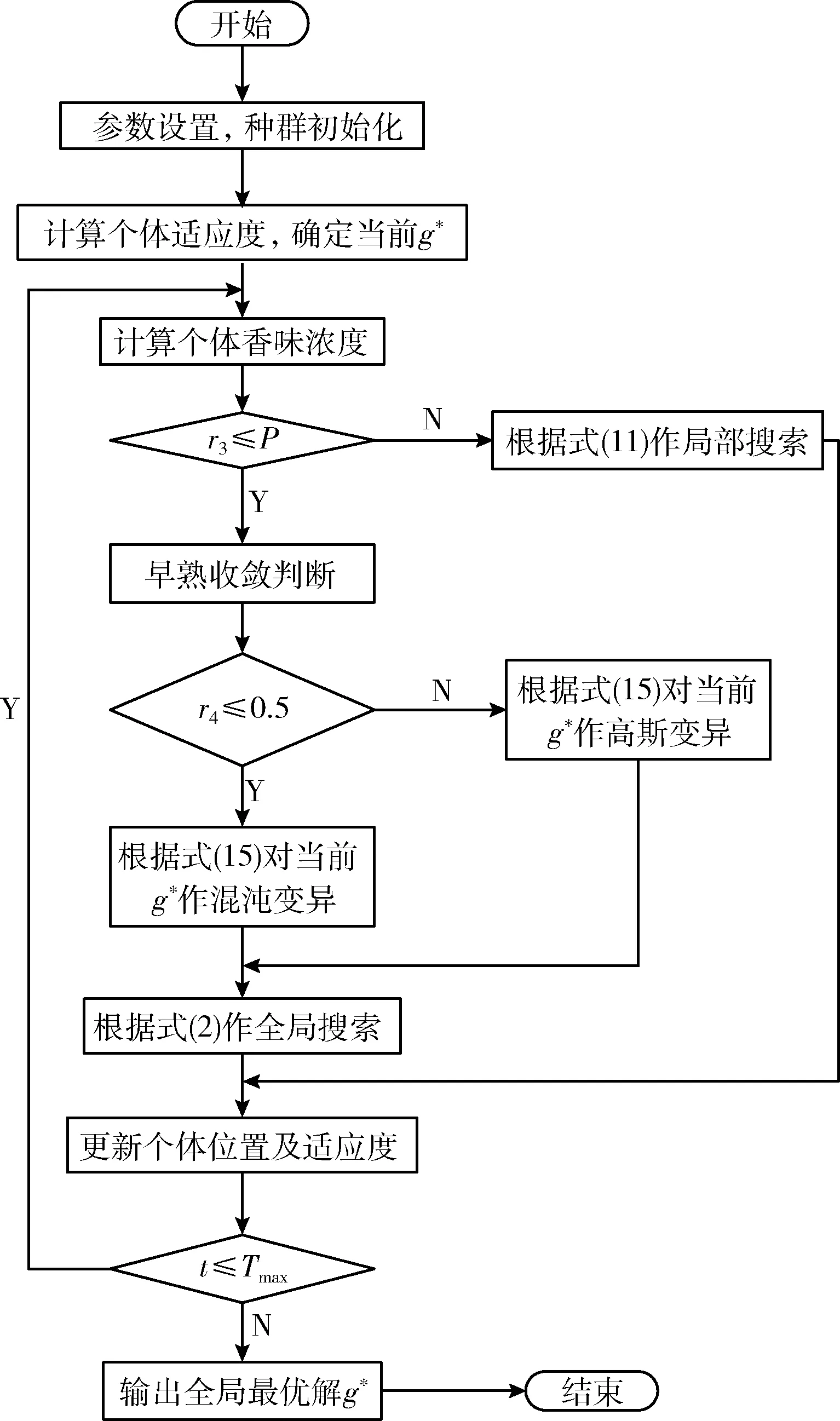
图1 LGBOA算法流程

LGBOA算法时间复杂度。令蝴蝶的种群规模为N，迭代最大次数为Tmax，搜索空间的位置维度为d。根据LGBOA算法的执行流程，种群初始化时间复杂度为O(N×d)， 计算所有种群个体适应度的时间复杂度为O(N×d)， 确定当前最优解g*的时间复杂度为O(N×d)， 计算所有个体香味浓度的时间复杂度为O(N×d)。 经过最大Tmax次迭代过程后，早熟收敛判断过程的时间复杂度为O(N×d×Tmax)， 高斯变异或混沌变异的最差时间复杂度为O(N×d×Tmax)。 综上，LGBOA算法的时间复杂度为O(N×d×Tmax)。 该时间复杂度与传统BOA算法的时间复杂度相同，说明改进算法在寻优性能提升的同时并没有增加计算代价。

3 LGBOA算法实验分析

3.1 实验环境

首先通过基准函数寻优测试验证LGBOA算法在求解优化问题上的可行性和有效性，利用表1中8种基准函数(代表智能算法中的适应度函数)进行寻优测试。前5种是单峰值函数，其分布特征是整个搜索区域内仅有一个最优值(最小)，即全局最优解，该类函数可以测试智能算法寻优过程中的搜索和收敛能力。后3种函数为多峰值函数，其分布特征是搜索区域内拥有多个局部最优值，该类型函数可以测试智能算法寻优过程中是否具有甄别局部最优、跳离局部最优，进行全局勘探的能力。实验的软硬件环境配置为：操作系统Microsoft Window 10，CPU为Intel Core I7，主频率为2.3 GHz，内存为8 GB，算法在MATLAB R2017平台上实现。选择CBOA算法[10]、ALBOA算法[11]和SIBOA算法[12]进行性能对比。CBOA算法利用混沌映射机制提升了BOA算法的全局搜索性能。ALBOA算法利用自适应学习机制改进蝴蝶优化算法，可以有效均衡全局搜索与局部开发的比例。SIBOA算法融合正余弦算子和混沌映射改进蝴蝶优化算法，通过ICMIC映射的种群初始化机制和飞行认知部分的正余弦寻优机制，有效提升了算法的寻优精度。每种算法独立运行20次，取平均值结果进行对比。相关参数中，种群规模设为30，最大迭代次数设为400。

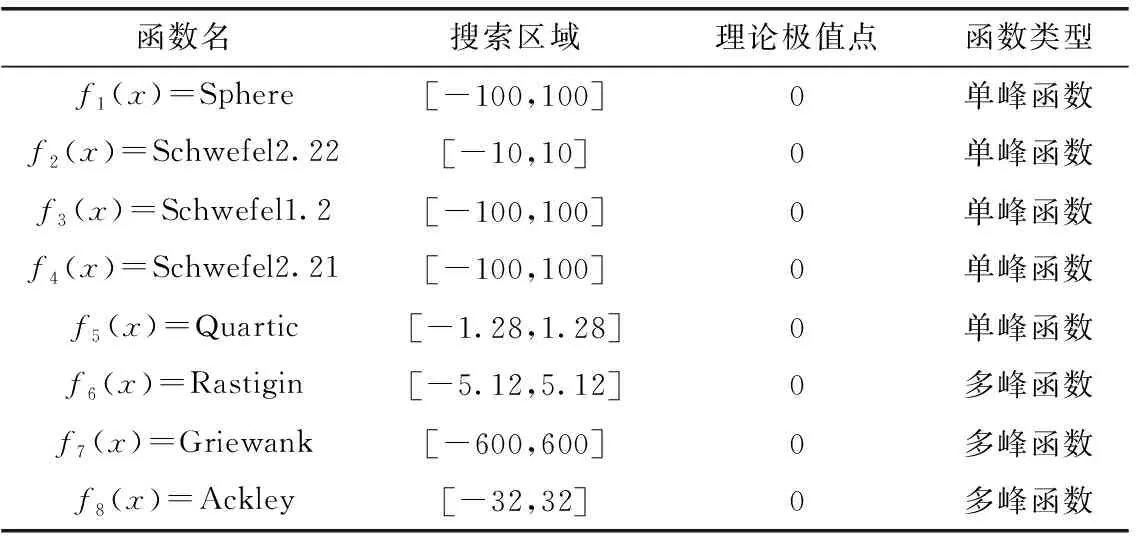
表1 基准函数特征

3.2 实验结果分析

实验1统计了CBOA算法、ALBOA算法和SIBOA算法以及本文的LGBOA算法在维度为30时，在8种基准函数下进行20次独立寻优时，得到的平均精度、标准差、最优解的对比结果，结果见表2。LGBOA算法在f1(x)、f2(x)、f5(x)、f6(x)、f7(x)和f8(x)上得到了理论最优解，在f3(x)和f4(x)上虽然没有得到理论最优解，但也是所有算法中寻精度最高的。在标准差指标上，LGBOA算法是所有算法中最低的，这充分说明算法的稳定性也是较好的。无论是处理单峰函数和多峰函数的寻优，都具有较好适应性。从寻优平均精度所提升的数量级上来讲，LGBOA算法平均可以提升20～65个数量级，充分说明LGBOA算法在基本BOA算法上所做的改进是更全面的，在提升收敛速度、全局寻优能力和避免局部最优等综合性能上是有效可行的。

表2 算法的寻优结果对比

实验2展示了CBOA、ALBOA和SIBOA及LGBOA算法的平均收敛曲线，结果如图2所示。从400次算法迭代后的寻优精度看，LGBOA算法在8个基准函数上都得到了最高的收敛精度，说明在单峰函数和多峰函数中，算法的适应性还是较好的，没有因为寻优峰值点的变化而发生变化。再对比收敛速度，LGBOA算法的曲线走势明显下降速度更快，说明算法的拓展空间能力更强，能够快速找到更好的解。同时，LGBOA算法在迭代前后阶段都保持有更好的寻优能力，尤其针对多峰值函数而言，没有出现局部极值点处的停滞现象。对于CBOA算法和ALBOA算法而言，寻优曲线在经过若干次迭代后，就已经趋于局部收敛状态，说明算法没有能力拓展新的空间，寻优精度无法提升。SIBOA算法的性能略要优于以上两种算法，但在迭代晚期寻优精度也基本停滞。LGBOA算法在多峰基准函数上的收敛曲线具有明显的局部停留后的下坠现象，说明该算法能够通过局部收敛状态判定，利用变异机制跳离局部最优解，从而进一步靠近理论最优值。

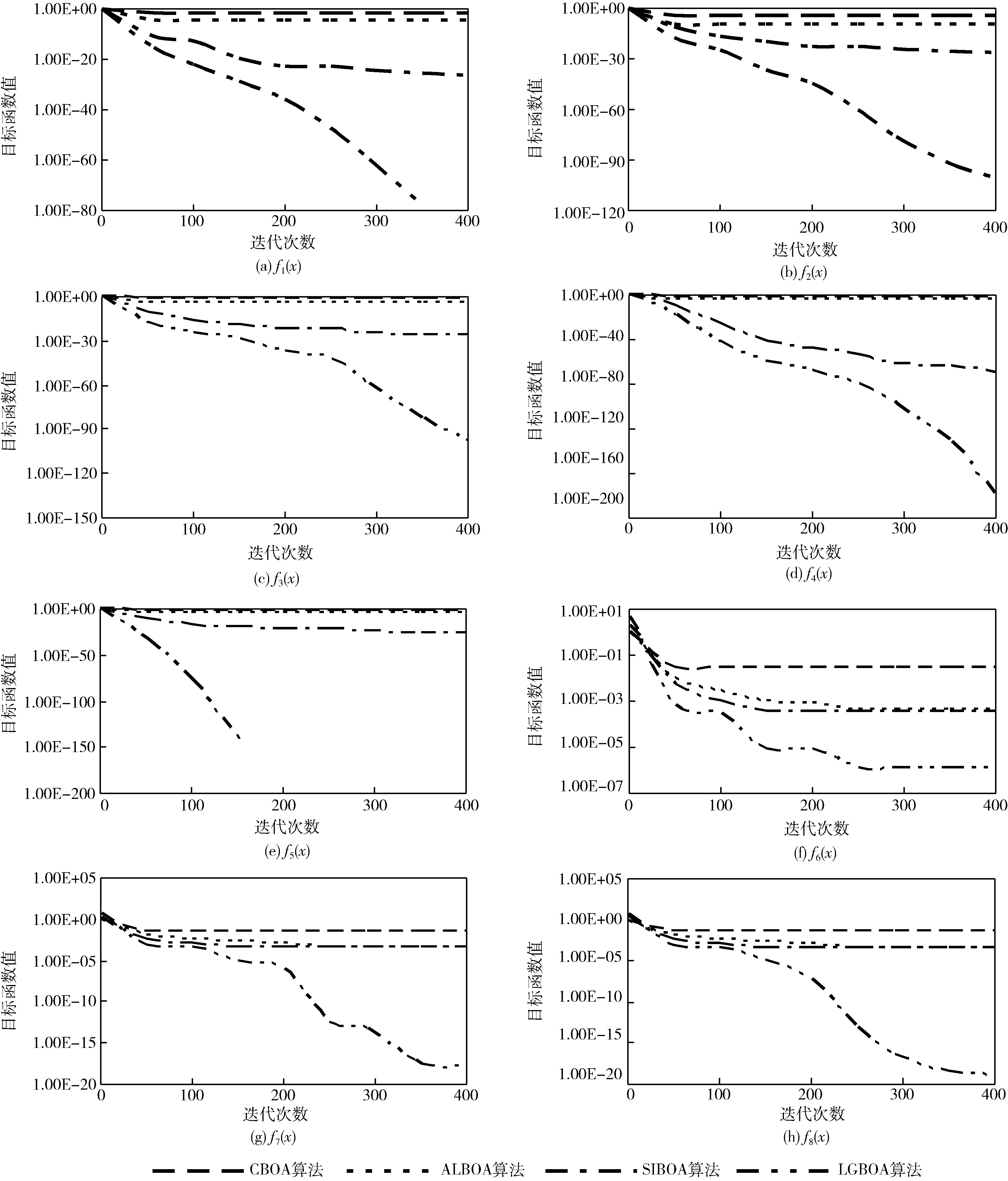
图2 寻优收敛曲线

实验3统计LGBOA算法相对其它3种算法的Wilcoxon秩和检验p值，结果见表3。该指标将LGBOA算法假设为最优算法，然后计算LGBOA/CBOA、LGBOA/ALBOA和LGBOA/SIBOA的秩和检验p值。研究表明，若p<0.05，则认为假设无法拒绝。可以看到，得到的p值均小于0.05，表明LGBOA算法的优越性在统计上是显著的。

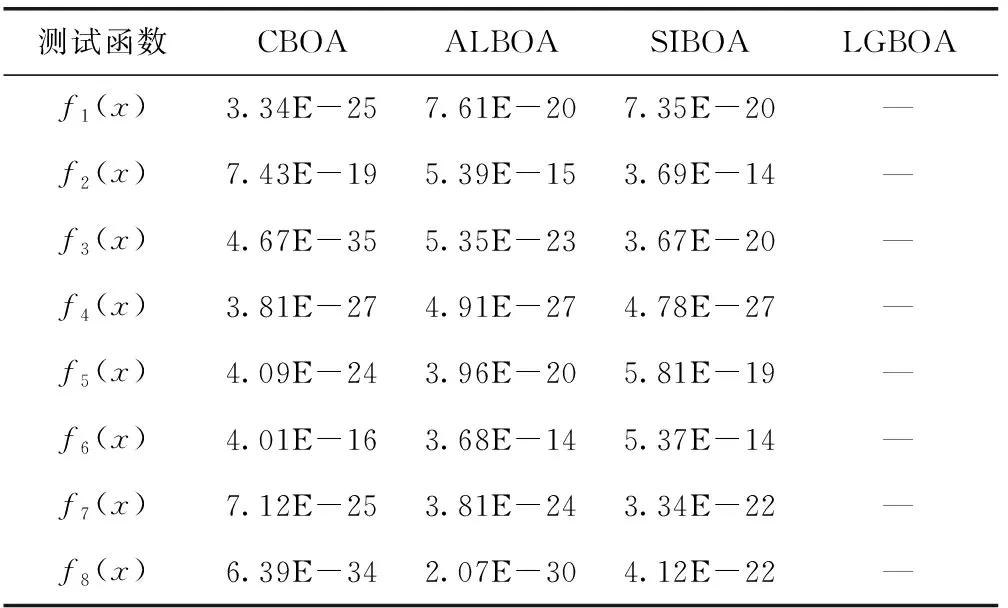
表3 Wilcoxon秩和检验p值

4 基于LGBOA算法优化SVM的土壤含水量预测模型

4.1 SVM回归模型

SVM(支持向量机)是一种基于统计理论的机器学习方法，其目标是通过非线性映射将模型输入映射至高维空间，构造超平面的决策曲面，以进行线性回归。SVM为了保证稀疏性，利用结构风险替代经验风险作为期望风险。具体过程如下：令数据样本D={(x1,y1),(x2,y2),…,(xm,ym)}，yi∈R。 模型学习目标为f(x)=wTx+b， 使f(x) 尽可能接近于y，而w和b为待定模型参数。令ε为支持向量回归SVR模型可接受的偏差。若 |f(x)-y|>ε， 需要计算SVR的预测损失。令ξi、ξ′i为两个松驰变量，则SVR可转换为二次规划问题，定义为

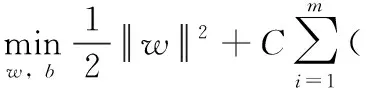
(18)

约束条件为

f(xi)-yi≤ε+ξi

(19)

yi-f(xi)≤ε+ξ′i

(20)

ξi≥0,ξ′i≥0,i=1,2,…,m

(21)

式中：C为控制误差的惩罚因子。SVR的对偶问题为

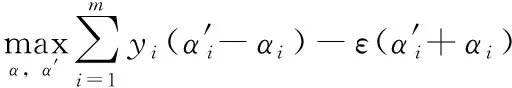
(22)

式中：αi、α′i为拉格朗日乘子。令K(x,xi) 为核函数，则决策函数为

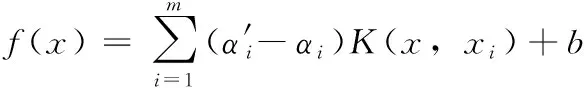
(23)

选择径向基核函数作为模型的核函数，即

(24)

式中：γ为核函数参数。由上述过程可知，惩罚因子C和核函数参数γ为影响SVM性能的主要因子，需要对其寻优后再确定SVM的最优模型，利用最优SVM模型对土壤含水量进行预测。

4.2 LGBOA-SVM算法

利用LGBOA算法对SVM模型的惩罚因子C和核函数参数γ进行寻优，以确定最优的SVM预测模型，进而对土壤含水量进行预测。LGBOA-SVM算法的过程如下：

步骤1 根据MIV方法，确定影响土壤含水量变化的气象因素，从而确定SVM的输入矢量；

步骤2 初始化LGBOA算法的初始参数，包括：种群规模N、激励指数a、感知形态c、概率阈值P、最大迭代次数Tmax、惩罚因子C和核函数参数γ的上下界；

步骤3 将原始数据集根据85%/15%的比例划分为训练样本集和测试样本集，并对数据进行标准化预处理；

步骤4 根据SVM模型的结构对蝴蝶个体位置进行编码。以均方误差函数MSE定义评估个体位置优劣的适应度函数，具体为

(25)

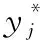
步骤5 初始化种群 {Xi,i=1,2,…,N}， 将蝴蝶个体位置编码为(C,γ)；

步骤6 根据均方误差函数MSE计算个体适应度，确定当前最优解，并计算个体香味浓度；

步骤7 若r3>P， 根据Levy飞行机制进行局部搜索位置更新，即式(11)；否则，转步骤8；

步骤8 进行早熟收敛条件判断，若满足局部收敛状态，转步骤9；

步骤9 若r4>0.5，根据式(15)对当前最优解进行混沌变异；否则，根据式(15)对当前最优解进行高斯变异；

步骤10 根据式(2)进行全局搜索，并更新个体位置及其适应度；

步骤11 判断个体位置是否超过(C,γ)的边界上下限，若出现越界，则以相应位置上下限修正个体位置；

步骤12 判断终止条件，若满足，返回至步骤7；否则，停止算法迭代，输出最优解X*=(C*,γ*)；

步骤13 以X*=(C*,γ*) 对SVM模型初始化，并利用训练样本和测试样本检测预测精度，得到土壤含水量预测值。

4.3 基于LGBOA-SVM的土壤含水量预测

影响土壤含水量的因素主要包括气象因素、土壤特征、植被状况以及人为活动因素等，其中，土壤特征和植被状况与具体区域和生物化学领域相关，本文主要探讨气象因素对土壤含水量的影响。气象因素主要有土壤含水量、降水量、空气湿度、气温、土壤温度、风速、光照等因素。为了对SVM的输入变量进行筛选，引入平均影响值MIV法评价气象因素的相关性，以此确定SVM的输入矢量。选取以上气象因素作为原始数据，基于MIV法进行输入矢量筛选的具体过程为：首先，输入以上变量至SVM模型训练，以原值为基础将相应变量分别增加和减少10%，形成两个新样本数据；然后，利用原始数据训练过的SVM对两个新样本数据进行测试，得出测试结果；最后，对于两次训练结果的差值，得出该变量的影响变化值IV，并求取在所有样本数据上的均值结果，即为一个影响因素所对应的MIV。选取MIV累计值在85%以上的变量作为筛选的变量数量。选取相关气象数据经过训练分析后，以MIV累计值85%为临界点，最终选取土壤含水量、降水量、空气湿度、气温、土壤温度、光照作为SVM的输入矢量，即预测因子。

此外，由于相关预测因子量纲不同，衡量单位不一，首先需要对原始数据进行归一化处理，将所有数据映射至统一区间[0,1]。利用max-min映射函数进行数据归一化处理，函数形式如下

(26)

式中：A′i表示预测因子归一化处理后的数值，Ai表示原始数值，minA表示每个预测因子的最小值，maxA表示每个预测因子的最大值。

基于LGBOA-SVM模型的土壤含水量预测过程如图3所示。

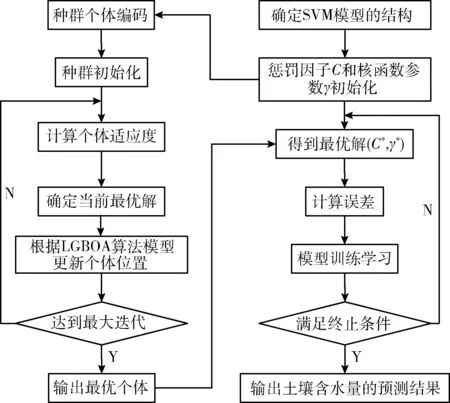
图3 基于LGBOA-SVM模型的土壤含水量预测流程

5 LGBOA-SVM预测模型实验分析

5.1 测试样本

选取国家气象科学数据网提供的各项气象数据来验证算法的可行性，具体选择中西部某县在2020年8月1日至2020年8月31日间的数据进行测试。以1 h为步长，每天选取24组数据，则8月整月的选取数据样本数为744组。利用max-min映射函数将数据样本标准化预处理后，将样本数据划分为训练样本集和测试样本集，随机选取644组数据为训练样本，剩余100组数据为测试样本。选取土壤含水量、降水量、空气湿度、气温、土壤温度、光照作为SVM模型的输入矢量。某一时刻的数据简况见表4。

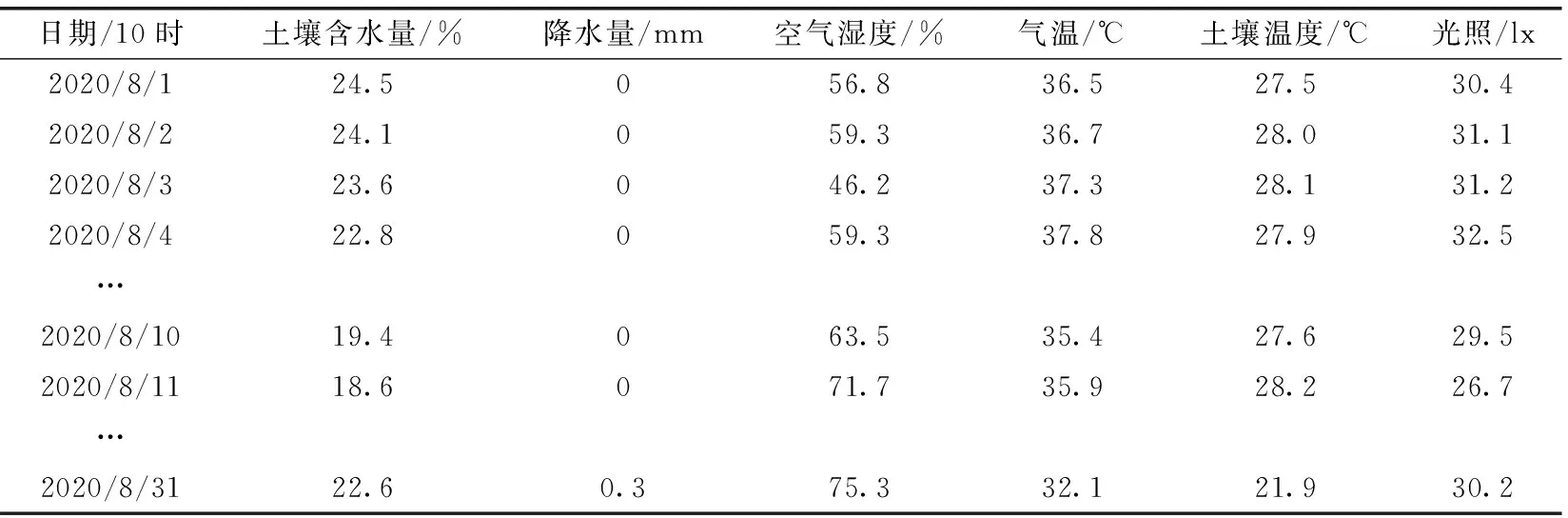
表4 部分原始数据样本

选择ISSA算法[7]、IGWO算法[8]和SIBOA算法[12]进行性能对比，将其与BP神经网络和SVM进行融合，利用ISSA-BP[7]、IGWO-BP[8]、SIBOA-SVM[12]以及本文的LGBOA-SVM这4种模型对土壤含水量进行预测。前两种算法ISSA、IGWO实现了对BP神经网络的连接权值和阈值的寻优，SIBOA则实现对SVM的惩罚因子和核函数参数的寻优。相关参数中，支持向量机SVM的核函数为径向基函数，设置惩罚因子和核函数参数的上下限为[2-7,27]。BP神经网络预测模型均为默认参数，训练目标误差为10-4，训练次数为1000，学习率为0.1。

5.2 实验结果

如图4所示的4张图是4种预测模型与土壤含水量的实际值在测试样本上的对比结果，实线表示实际值，虚线表示模型预测值。对比图4(a)、图4(b)，IGWO-BP预测模型的结果更靠近实际值，且有个别样本点是基本重合的，说明IGWO-BP的预测精度高于ISSA-BP。对比图4(b)、图4(c)，在使用了不同的预测模型后，SIBOA-SVM预测模型则更加接近实际值，虚线趋势基本保持着与实线一致，BP神经网络的预测性能还有待提高。再对比图4(d)，可以看到，LGBOA-SVM模型所预测的土壤含水量是所有算法中最接近于实际值的，虚线、实线之间的重合度明显提高，多数样本点的预测值与实际值基本重合，其预测精度通过改进的蝴蝶优化算法的寻优性能得到了有效的提升。

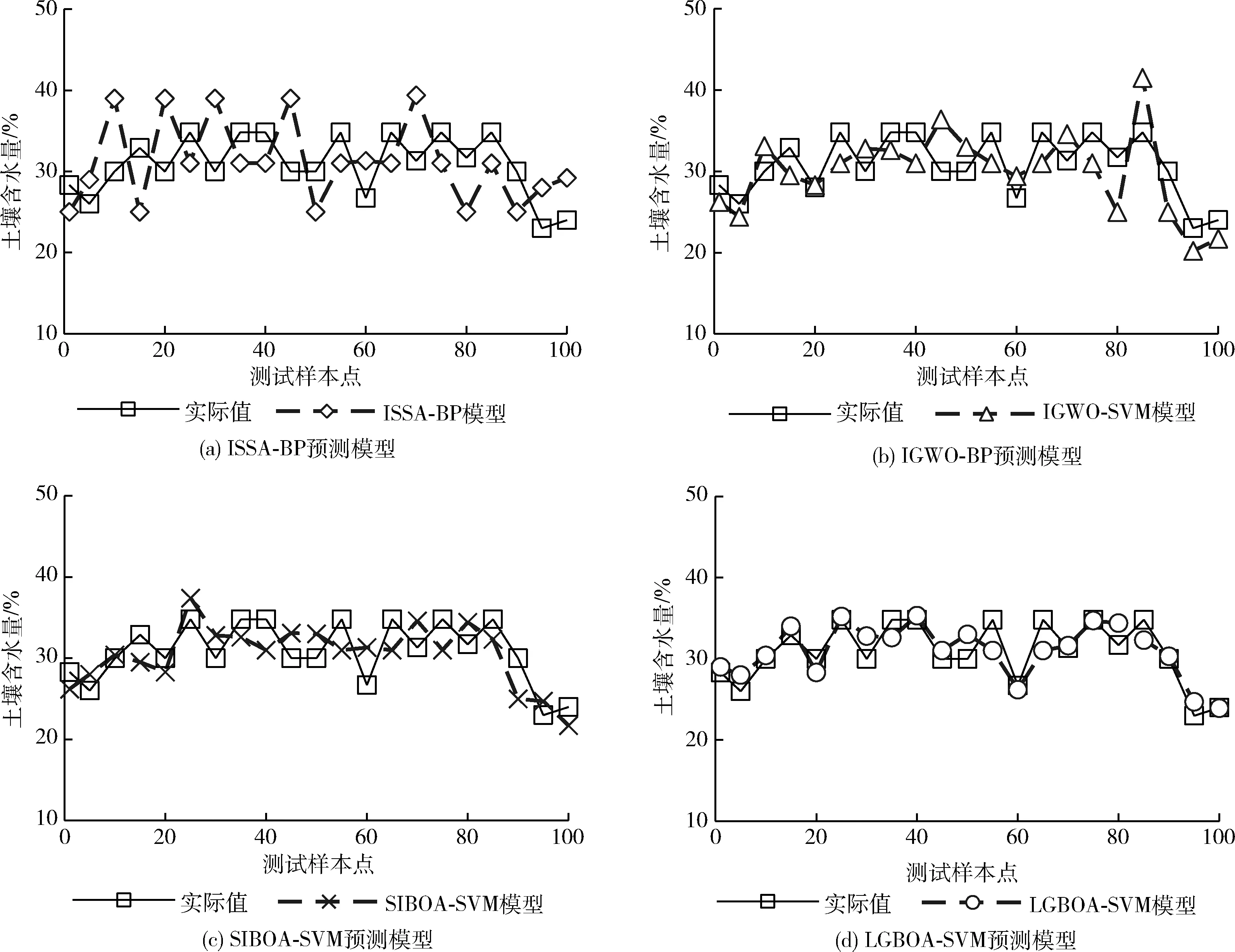
图4 预测结果对比

为了更清楚分辨预测模型在100个测试样本数据上预测值与实际值间的差距，本部分将统计出每种预测模型所求的预测值与实际值的比值大小，并统计出在不同的比值区间内4种预测模型在100个测试样本数据上的数量分布情况，并绘制柱形图，结果如图5所示。可以看到，本文的LGBOA-SVM模型的预测值与实际值的差值比值小于10%的样本点个数接近于总测试样本的三分之二，是所有算法中最高的。在小于10%这个区间内，优化后的SVM预测模型较优化的BP神经网络模型略有优势，也从侧面验证BP在泛化能力上略有不足。10%～20%区间内，LGBOA-SVM和SIBOA-SVM基本保持持平，ISSA-BP和IGWO-BP则在该区间内的样本点分布明显更多。20%～30%区间内，4种模型的样本点分布差异较大。30%～40%区间内，4种模型基本接近，IGWO-BP略高。大于40%的区间内，本文的LGBOA-SVM的样本点分布依然是最少的，说明LGBOA-SVM模型的具有更高的预测准确率。

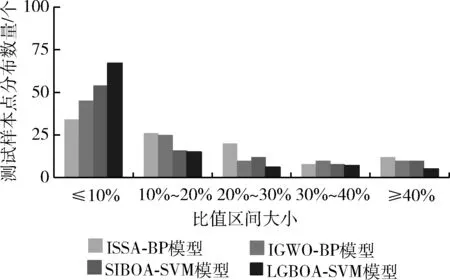
图5 不同预测模型的差值分布

进一步引入平均相对误差MAPE、平均绝对误差MAE和均方根误差RMSE定量分析模型预测精度，定义如下

(27)

(28)

(29)

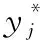
表5是测试指标10次实验的均值结果。从MAPE看，仅有LGBOA-SVM和SIBOA-SVM的平均相对误差在10%以内，该误差范围验证预测精度较为可观，若高于15%～20%，则预测值的误差就较大，已无参考意义。具体地，在100组测试样本数据中，LGBOA-SVM模型的测试中有86组数据得到了低于10%的平均相对误差，剩下14组数据均高于10%，精准预测率占测试样本的86%，这是4种算法中最多的。而MAE和RMSE的计算结果也辅证了LGBOA-SVM的优越性。

表5 性能表现

进一步通过算法寻优适应度的变化观察模型收敛速度，以验证算法的效率提升情况，结果如图6。根据式(25)所定义的适应度，适应度值越小，表明预测模型计算的土壤含水量预测值误差越小，模型性能越好。图6表明，在400次迭代过程中，LGBOA-SVM的适应度均值是最小的，且可以在约100次迭代时收敛到最优解，说明此时求得了SVM预测模型的最优惩罚因子C和核函数参数γ。ISSA-BP模型、IGWO-BP模型、SIBOA-SVM模型分别迭代至约300次、250次和180次时发生收敛。综合来看，利用Levy飞行和高斯混沌变异后的蝴蝶优化算法对于支持向量机SVM的优化效果还是很可观的，有效提升了算法寻优精度和收敛速度，进而在融入SVM后能够更准确对土壤含水量做出预测。

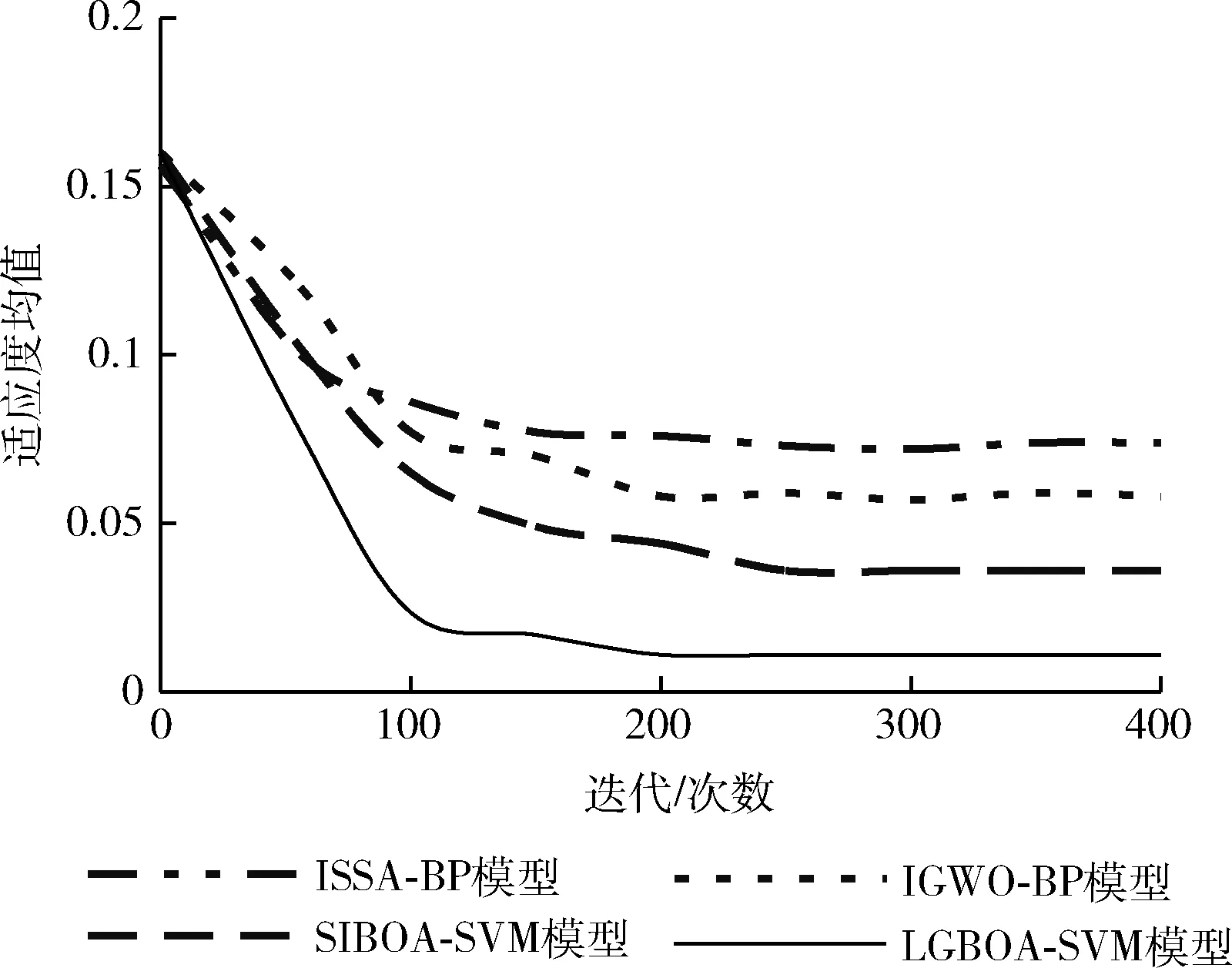
图6 不同模型的适应度均值

6 结束语

针对传统土壤含水量预测方法精度低、效率差的不足，提出改进蝴蝶算法优化支持向量机SVM的土壤含水量预测算法。首先引入Levy飞行策略和高斯混沌变异机制对传统蝴蝶优化算法的寻优能力进行了优化。然后利用改进蝴蝶优化算法优化支持向量机SVM模型，并构建土壤含水量预测模型。基准函数测试验证改进蝴蝶优化算法可以有效提升收敛速度和寻优精度，而土壤气象样本数据集也验证改进模型可以有效提高土壤含水量预测精度和效率。未来的研究方向可集中在除考虑气象因素以外，将土壤物理、化学特征考虑进来，利用成分分析法建构更全面的预测模型，同时进一步改进智能算法的寻优效率，以提升土壤含水量预测精准度。