融合时空网络和自注意力的兴趣点序列推荐
朱建豪,马文明,王 冰,武 聪
(烟台大学 计算机与控制工程学院,山东 烟台 264005)
0 引 言
在现实生活中,用户的签到行为通常发生在一个序列中,推荐系统通过用户的历史签到记录和当前的签到状态,来为用户推荐接下来可能去的兴趣点。目前先进的序列推荐算法通过综合计算用户的长期偏好和短期偏好进行POI推荐,比如用户X是一个体育爱好者,平时喜欢去篮球场打篮球,当他放假准备行李坐飞机外出旅游时,推荐系统会根据用户短期偏好进行相关景点推荐,而不会根据用户长期偏好进行篮球场等相关地点推荐。然而目前序列推荐算法存在一些问题,没有考虑有效利用用户签到地点之间的时间和空间间隔的信息,不能够准确地表达用户的偏好,用户的签到行为可能为用户提供了关键信息,比如用户V星期五公司下班后,习惯去公司周围篮球场打篮球,然后在附近餐厅吃饭,到了星期六,用户会在家周围的篮球场打篮球并在附近餐厅吃饭,这种签到之间的时间间隔和空间间隔信息会为用户推荐在篮球场附近的餐厅以及下一步的行动[1,2]。
为此,本文提出一种融合时空网络和自注意力的兴趣点序列推荐系统模型(sequential recommendation of point of interest combines spatio-temporal network with self-attention,STSASP),为用户推荐一个POI序列。以经纬度表示POI的地理位置,计算用户签到行为之间的时间间隔以及签到地点之间的空间间隔,将时空间隔信息融入门控循环单元(gated recurrent unit,GRU)模型中,捕捉用户反馈数据的序列性,同时使用自注意力(self-attention)机制在签到序列上为每次签到分配不同的权重,反映用户的长期偏好,最后通过时空间隔信息为用户匹配POI序列。
1 相关工作
传统的推荐系统分为:基于内容的推荐系统和协同过滤的推荐系统,都是以静态方式对用户反馈数据进行建模,只能捕获用户的一般偏好。随着时间的推移,用户的交互行为和用户的偏好很有可能发生改变,传统的推荐系统忽略了用户偏好的动态变化,所以传统的推荐系统不能有效地处理POI推荐问题。
序列推荐系统把用户历史数据看作一个动态序列,在用户项目序列中,通过考虑用户顺序行为和历史数据的相互依赖性预测用户的偏好,从而更加精确地进行推荐[3]。序列推荐主要有两种模型:基于马尔可夫[4]的模型和基于深度学习[5]的模型。马尔可夫模型通过转移概率矩阵预测下一个行为的概率,但由于序列数据的稀疏性,FPMC[6]模型被提出,该方法将矩阵分解机和马尔可夫链相结合提取序列信息,考虑用户偏好。但是在处理高阶顺序依赖关系时,高阶马尔可夫链[7]模型因参数数量随阶数指数增长,其分析历史状态有限。因此基于深度学习的序列推荐系统模型迅速发展起来,其中循环神经网络(recurrent neural network,RNN)[8]最具有代表性并在各个应用上表现良好。然而随着输入序列长度的增加,RNN无法学习和利用前面的信息,面临着长期依赖、梯度爆炸问题[9],文献[10,11]分别使用长短期记忆模型(long-short term memory,LSTM)和门控循环单元模型来解决这一问题,它们能够对有价值的交互信息进行长期记忆,并且可以较好地解决梯度消失和爆炸问题,从而提升网络模型的学习能力。
进一步研究发现,将时间和空间信息融入模型中能够提升推荐结果。STRNN[12]将时间和空间信息融入到循环神经网络,考虑连续两次交互的时间和距离间隔,通过转移矩阵融合时空信息。LSTPM[13]聚集用户最近访问位置,将地理因素融入RNN中。Time-LSTM[14]在LSTM中加入时间门。STGN[15]通过添加时空门进一步增强了LSTM结构。但是由于RNN的超强假设,序列中任何相邻的交互假设都是相互依赖的,容易产生错误的依赖关系。注意力机制[16]能够为不同的序列数据赋予不同的权重,有效捕捉用户长序列数据之间的相互依赖。SASRec[17]使用自注意力进行序列推荐,DeepMove[18]通过注意层和循环层学习长期周期性和短期序列规律。ATST-LSTM[19]使用注意力机制为每个交互分配不同的权重,但只考虑了连续访问。CSALSR[20]融合自注意力机制与长短期偏好进行序列推荐,但是没有考虑时间间隔和空间间隔的信息。
2 时空网络自注意力模型
2.1 问题描述和问题定义
2.1.1 问题描述
在融合时空网络和自注意力的兴趣点序列推荐系统模型中,模型通过用户的历史签到序列数据,预测用户接下来将要去的3个连续地点的POI序列,比如用户去过的签到序列为 [Pseq1,Pseq2,Pseq3,…,PseqH], 需要预测的POI序列为Pj=[PseqH+1,PseqH+2,PseqH+3]。
2.1.2 问题定义

(1)
(2)
(3)
其中,r为地球半径6371 KM。计算地点集合P=[P1,P2,P3,…,PM] 中每个地点与用户签到序列C(Ui)=[Pseq1,Pseq2,Pseq3,…,PseqH] 中每个地点的空间距离,计算3次来填充矩阵,用E(N)表示;计算POI序列Pj=[PseqH+1,PseqH+2,PseqH+3] 中每次签到与签到序列中 [Pseq1,Pseq2,Pseq3,…,PseqH] 中每次签到的时间间隔,计算M次来填充矩阵,用E(S)表示,E(S),E(N)∈R3*M*H。
2.2 模型结构
本文提出了融合时空网络和自注意力的兴趣点序列推荐系统模型,模型的输入为用户的历史签到数据Pseqi=[Ui,Pi,Ti] 和地点数据Pi=[Pi,lngi,lati], 将数据通过Embedding层,接着将用户签到序列以及时间间隔和空间间隔信息通过GRU模型,然后通过自注意力机制对签到时序地点进行建模,得到用户签到序列的更新表示,最后通过兴趣点匹配候选地点,模型的输出为包含3个连续地点的POI序列。模型结构如图1所示。
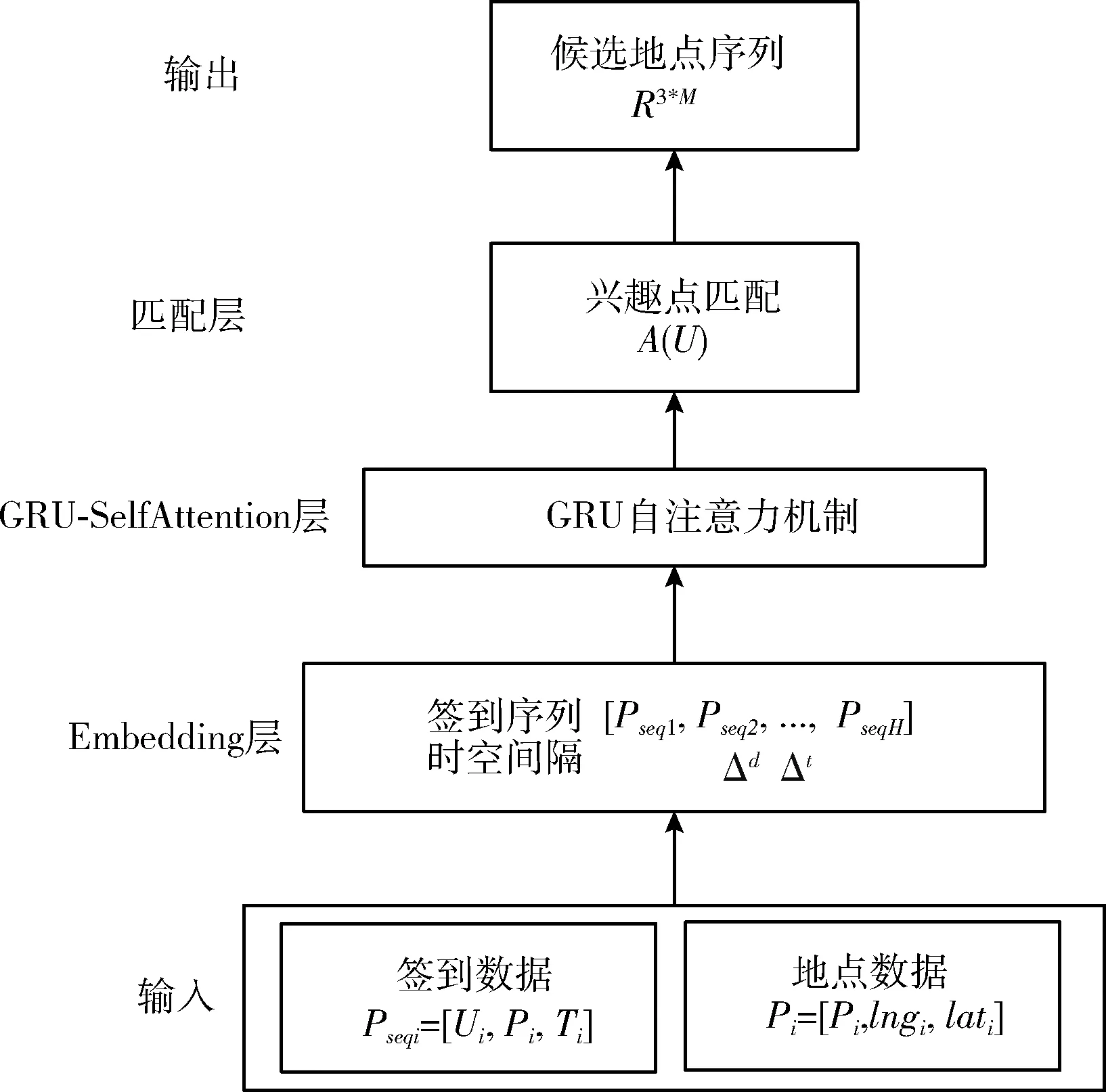
图1 模型结构
2.2.1 Embedding层
将用户历史签到数据中的用户、地点和时间进行Embedding,转化为密集Embedding表示,以向量化的形式输入到网络模型中。Embedding层的输出为C(Ui)=[Pseq1,Pseq2,Pseq3,…,PseqH]。
2.2.2 GRU-SelfAttention层
GRU模型能够很好地学习和利用用户的历史签到序列数据,在每一步接收序列中的数据输入和上一个隐藏层的输出,并输出到隐藏层,将用户签到序列的时间间隔和空间间隔信息融入GRU模型中,增加时间门和空间门后的GRU模型结构如图2所示。

图2 GRU模型结构
rt=σ(Wr[ht-1,xt])
(4)
zt=σ(Wz[ht-1,xt])
(5)
Tt=σ(Wt[xt,Δt])
(6)
Dt=σ(Wd[xt,Δd])
(7)
h′t=tanh(Wh′[rt*ht-1,xt*Tt*Dt])
(8)
ht=zt*h′t+(1-zt)*ht-1
(9)
yt=σ(Wyht)
(10)
其中,xt和ht-1分别表示当前时间t的输入向量和上一时间t-1的输入向量,rt和zt分别表示重置门和更新门,通过xt和ht-1来获取两个门的状态。Tt和Dt分别表示时间门和空间门,将用户签到地点之间的时间间隔和空间间隔信息融入到GRU模型中,Tt和Dt分别控制当前地点的时间信息和空间信息对将来POI推荐的影响。其中Δt,Δd分别表示两个地点之间的时间间隔和空间间隔。Δd通过两个地点经纬度坐标的Haversine距离公式计算得到,Δt通过两个地点之间时间差得到。xt*Tt*Dt表示通过时间门Tt和空间门Dt控制当前地点的时间和空间信息对于POI推荐的影响。σ和tanh分别代表sigmoid激活函数和tanh激活函数,Wr,Wz,Wt,Wd,Wh′,Wy为权重矩阵,*表示基于矩阵元素中对应元素相乘运算。rt*ht-1表示通过重置门rt控制上一时间输入需保留的信息,再与当前输入进行拼接。zt*h′t通过更新门zt控制当前时间输入的信息量,进行选择性记忆,后半部分再通过1-zt选择性遗忘上一时间输入的信息量。yt∈RH*d表示模型的输出。
在POI序列推荐的预测中,用户的历史签到地点中可能只有某些地点对预测的POI序列有影响,因此,引入注意力机制,可以帮助模型为用户签到数据赋予不同的权重,动态地捕捉每一个用户的重点信息。
自注意力机制是一种特殊的注意力机制[21],在动态赋予权重的同时,捕捉了用户反馈数据之间的相互依赖,并在长序列的数据上表现出色,因此,本文考虑将自注意力机制应用于用户签到反馈数据,在用户签到序列内为每次访问分配不同的权重。Query,Key,Value分别表示自注意力机制中的查询、索引、需要被加权的数据。yt∈RH*d表示GRU模型的输出,GRU-SelfAttention层的结构如图3所示。

图3 GRU-SelfAttention层结构
Q′=WQyt
(11)
K′=WKyt
(12)
V′=WVyt
(13)
(14)

2.2.3 兴趣点匹配层
根据GRU-SelfAttention层输出的用户签到长期偏好表示S(U)∈RH*d, 以及地点矩阵E(P)∈R3*M*d, 时空间隔矩阵E(S),E(N)∈R3*M*H, 从所有地点中为用户选出将来可能去的POI序列
(15)
A(U)=Sum(softmax(B(U)))
(16)
Sum运算是最后一个维度的加权和,将A(U)的维度转化成R3*M。
2.2.4 损失函数
POI序列推荐属于隐反馈推荐模型,将用户没去过的地点随机设置为负样本。给出用户签到序列C(Ui), 候选地点Pj=[PseqH+1,PseqH+2,PseqH+3]∈A(Ui), 其中j∈[1,M],Pk表示正样本,模型使用交叉熵损失函数进行训练
(17)
2.2.5 算法设计
在融合时空网络和自注意力的兴趣点序列推荐系统模型中,用户序列数据构造和模型训练过程如算法1所示。
算法1:STSASP算法
输入:用户签到数据,地点位置信息
输出:用户的签到序列,推荐POI序列
//构造训练数据
(1)For user in (1, number):
(2) Check-in order by time
(3)Pi=(lngi,lati)


(6)C(Ui)=[Pseq1,Pseq2,Pseq3,…,PseqH]
(7)End
//模型训练
(8)For a in (1, epoch):
(9) For b in (1,batch):
(10) POI=Model(C(Ui),Δt,Δd)
(11) Select the POI sequence from all locations
(12) Loss=Loss(POI,Label)
(13) Recommend POI sequence in different K
(14)Recall@K=(POI,Label)
(15) End
(16)End
在STSASP算法中,首先将输入的用户签到序列数据按照时间顺序进行升序排序,然后根据地点的地理位置信息和签到时间信息计算空间距离和时间间隔,构造每一个用户的签到序列。接着将用户签到序列信息以及时空间隔信息送入模型中进行训练,计算损失函数,从所有的候选地点中为推荐POI序列,通过不同的前K项值来比较实验结果,最后以召回率为评价指标和其它算法进行对比。本算法的时间复杂度T(n)=O(n2), 空间复杂度S(n)=O(n)。
3 实 验
3.1 实验配置
3.1.1 数据集
本文在真实签到数据集Foursquare[22]和Gowalla[23]上进行训练和测试。Foursquare数据集是用户在纽约市长期登机签到加密数据集。Gowalla数据集是社交签到类应用场景下的用户行为日志。剔除在数据集中出现次数少于10次的地点,将用户签到序列中的地点按照签到时间顺序升序排列。将连续的时间戳分为7*24=168维,表示用户一天或一周的签到行为,用来反映周期性。将80%数据作为训练集,20%数据作为测试集。训练时,将用户签到序列前h项作为签到数据,比如 [Pseq1,Pseq2,Pseq3,…,Pseqh],h后3个地点作为将要去的包含3个连续地点的POI序列,比如 [Pseqh+1,Pseqh+2,Pseqh+3]。 数据集的基本数据信息:用户、地点、签到见表1。

表1 数据集基本信息
3.1.2 评价指标
针对上述数据集,本文选择召回率(Recall)作为评价指标,Recall@K表示为用户推荐前K项中的正样本在原始正样本中的比例。为用户推荐一个包含3个连续地点的POI序列,召回率越高,表示推荐结果越好
(18)
3.1.3 参数设置
本文使用Adam优化器进行模型优化训练,学习率为0.003,迭代训练次数为20,丢弃率Dropout[24]为0.2,每个batch的大小为1024,模型Embedding的维度为50,负样本数量为10。
3.2 实验分析
3.2.1 本文实验
本文首先考虑为用户推荐不同长度地点的POI序列,POI序列长度分别为1个地点,包含2个连续地点的POI序列,包含3个连续地点的POI序列,图4(a)和图4(b)分别展示了以召回率@K为评价指标,在Foursquare数据集和Gowalla数据集上,STSASP模型为用户推荐不同长度地点的POI序列的表现。

图4 在Foursquare和Gowalla数据集上不同K值的召回率
1个POI、2个POI、3个POI分别表示为用户推荐1个POI、2个连续地点的POI序列、3个连续地点的POI序列。实验结果表明,为用户连续推荐多个POI时,Recall@K会有一定程度的下降。在POI序列推荐中,顺序因素为关键,要求推荐的POI序列是用户将来连续要去的地点,并且顺序要对应正确,所以为用户推荐3个地点的POI序列相比与较少地点的POI序列在召回率上会相应下降。不同的K值对于POI序列推荐的结果是不同的,在Foursquare和Gowalla数据集中,随着K值的增大,为用户推荐前K项中的正样本在原始正样本中的比例也在增大,召回率也会相应的增大。本文最终选择为用户推荐1个包含3个地点的POI序列。
3.2.2 对比实验
为了验证STSASP模型的推荐效果,将STSASP模型与其它6种地点推荐算法分别在Foursquare和Gowalla数据集上进行比较和分析:
(1)BPR[25]。该方法将贝叶斯个性化排名与矩阵分解相结合,分析潜在语义信息。
(2)FPMC。该方法将矩阵分解机和马尔可夫链相结合,捕获用户顺序行为。
(3)STRNN。该方法是在循环神经网络中融合时空信息特征的地点推荐算法。
(4)DeepMove。该方法通过注意力循环网络来进行地点推荐,捕获用户行为周期性。
(5)LSTPM。该方法结合了长期和短期顺序模型进行地点推荐。
(6)CSALSR。该方法是融合自注意力机制和长短期偏好的序列推荐模型。
表2和图5展示了以召回率@5和召回率@10为评价指标,各方法在Foursquare和Gowalla数据集上的表现。

图5 各方法在Foursquare和Gowalla数据集上的表现

表2 各方法在Foursquare和Gowalla数据集上的表现
实验结果表明,基于深度学习的序列推荐系统模型优于传统马尔可夫序列推荐模型,主要原因是深度学习模型通过非线性方式对用户地点进行建模,能够捕获到序列中的复杂关系,同时在模型训练过程中,通过正则化、Dropout等技术避免过拟合,能够提高模型鲁棒性。
STSASP在整体上都优于融合自注意力机制和长短期偏好的CSALSR模型,STSASP在Foursquare数据集上为用户推荐3个连续地点的POI序列的召回率@5和召回率@10分别为0.131、0.194,在Gowalla数据集上分别为0.103、0.151,相比于CSALSR模型,STSASP在Foursquare数据集上和Gowalla数据集上的召回率分别提升了19.63%、22.01%和10.75%、11.02%。实验结果表明,相比于CSALSR通过融合自注意力机制和长短期偏好,忽略了时间间隔和空间间隔信息进行序列推荐,STSASP从用户签到反馈序列数据中提取了有效的时间和空间信息,更充分地获取了用户的偏好,召回率更高,推荐结果更好。
3.2.3 超参数分析
Embedding的维度参数对模型的效果存在影响,保持其它参数不变,在召回率@20时,选择不同维度参数d在数据集上进行实验。图6展示了关于超参数分析的实验结果。图6(a)反映了维度参数d在不同数据集上对模型推荐效果的影响,可以发现,高维度能够更精确地表达用户和地点,有助于模型历史信息地交互。随着维度的增加,召回率在相应地提高,但是更大的维度不一定能带来更好的模型性能。在本文中,设置维度参数d为50。模型的丢弃率Dropout对模型的效果存在影响,由图6(b)可知当Dropout为0.2时,模型有较好的效果。

图6 超参数分析
3.2.4 消融实验
STSASP1为STSASP消去时间间隔和空间间隔的模型,由图7可知,STSASP1模型在失去时空间隔信息后,无法有效地表达用户的偏好,因此表现不佳,在Foursquare和Gowalla数据集上的Recall@5和Recall@10上分别降低了27.48%、23.71%和20.42%、19.03%,在K大于20后,Gowalla数据集中STSASP1与STSASP的差距越来越大,原因是在多地点的环境中,时空因素对推荐结果的影响更大。通过比较发现CLALSR模型效果略优于STSASP1,因此说明了时间间隔和空间间隔对模型的重要性。

图7 Foursquare和Gowalla数据集上STSASP和STSASP1不同K值的召回率
4 结束语
本文提出了融合时空网络和自注意力的兴趣点序列推荐系统模型,模型用于预测用户将来要去的POI序列。本模型将用户签到序列的时间和空间间隔信息融入GRU模型中,然后通过自注意力机制对签到时序地点进行建模,得到用户的长期偏好序列,最后通过签到地点与候选地点的时间间隔和空间间隔匹配候选地点,为用户推荐包含3个连续地点的POI序列,更好地解决了POI序列推荐问题。在Foursquare数据集和Gowalla数据集上进行测试和验证,实验结果表明本文提出的STSASP模型优于之前提出的先进的模型。同时通过消融实验,验证了时间间隔和空间间隔因素在兴趣点序列推荐模型中的重要性。在今后的工作中,将考虑进一步优化网络结构,优化算法的时间复杂度和空间复杂度,从而进一步提升模型性能和推荐精度。

