面向多元时间序列的群体因果关系发现算法

蔡瑞初，伍运金，陈薇，郝志峰，2

（1.广东工业大学 计算机学院，广州 510006；2.汕头大学 理学院，广东 汕头 515063）

0 概述

因果发现旨在从观测数据中发现变量之间的因果关系，可以揭露数据的生成机制，帮助人们理解数据，辅助人们进行干预和决策［1］。近年来，因果关系在深度学习［2］、金融经济［3］、神经科学［4］、生物信息学［5］、社会科学［6］等领域受到了广泛关注。

当观测数据是多元时间序列数据时，现有的时序因果发现算法［7-10］通常认为个体之间是独立的，为每一个个体的多元时间序列数据单独学习一个因果关系作为该个体背后的因果关系，而个体间的因果关系学习过程是彼此无关的。然而在实际中，个体之间可能存在相同的因果关系。举例来说，在电商场景下，同一群体中的个体的购买行为可能具有相同的思维方式，如对于家庭群体的个体是否购买某个商品的影响变量是商品的质量，而对于普通家庭群体的个体是否购买某个商品的影响变量则是商品的质量和价格。

因此，来源于不同群体的个体的数据背后会具有不同的因果关系（产生机制），而相同群体的个体的数据背后会具有相同的因果关系。如果能知道哪些个体属于同一群体，便能利用群体内多个独立同分布的个体数据一起学习该群体共同的因果关系。然而，在实际中无法预先知道不同个体是否属于相同群体，也无法判断总共有多少个群体。

针对上述问题，本文提出一种面向多元时间序列数据的群体因果关系发现算法。首先基于因果关系的相似性，将所有个体划分成多个群体且无须指定群体的个数。对于每一个群体，使用变分推断方法学习群体因果关系，从而充分利用多个个体数据。当所有个体均在一个群体时，该算法利用所有个体数据共同学习一个因果关系。当一个群体内只有一个个体时，该算法与现有时序因果关系发现算法类似，仅利用单个个体数据单独学习一个因果关系。

1 相关工作

因果关系发现算法按照观测数据的类型可以分为基于非时序数据的因果发现方法和基于时序数据的因果发现方法［11］。

基于非时序数据的因果发现方法中包括基于约束的方法［12］、基于评分的方法［13］和基于函数的方法［14-16］。基于约束的方法利用（条件）独立性检验来判断变量之间是否存在因果关系，而基于评分的方法通过给DAG 打分并寻找得分最高的DAG 作为变量间的因果关系，但2 种方法都存在马尔可夫等价类的问题。为了解决这个问题，学者们提出了基于函数的方法，此类方法从数据产生机制出发，假设原因变量与结果变量存在函数映射，以及存在与原因变量独立的噪声变量，通过原因与噪声的独立性来识别因果关系。基于函数的方法包括线性非高斯无环模型（Linear Non-Gaussan Acyclic Model，LiNGAM）［14］、非线性加性噪声模型（nonlinear Additive Noise Model，ANM）［15］和后非线性因果模型（Post-NonLinear causal model，PNL）［16］。

上述基于非时序数据的因果发现方法也被拓展到了时序数据上，如同样基于约束的PCMCI算法［8］、基于评分的DYNOTEARS算法［9］和基于函数的VAR-LiNGAM算法［10］。PCMCI 算法基于条件独立性测试框架，使用PC 算法［17］发现变量的马尔可夫等价类集合从而缩短条件集，进一步用瞬时条件独立性（Momentary Conditional Independence，MCI）检验降低误发现率。DYNOTEARS算法从优化问题的角度出发，最小化一个带无环约束的损失函数，从而学习变量之间的瞬时影响和时延影响。VAR-LiNGAM 算法结合自回归模型和线性非高斯无环模型来识别变量的瞬时和时延因果关系的影响权重，并通过非高斯性假设保证了算法的可识别性。

目前一些工作［4，18］也考虑到了不同个体的样本背后的因果关系可能存在一定共性，并尝试从这种混杂样本中将样本划分成不同类别并学习因果关系。文献［4］与本文工作同样是面向多元时间序列数据，但其需要指定群体个数，并在此基础上学习个体特定的因果关系和共性的因果关系，再基于共性的因果关系计算某个个体属于不同群体的概率。文献［4］与本文工作的不同之处在于，其学习的是个体个性的因果关系以及个体间共性的因果关系，认为不同个体背后的因果关系仍然是不同的，仅是存在一定的共性因果关系，并基于共性进行聚类。本文工作则是在个体间的因果关系可能相同的场景下，对多个个体聚类并学习群体因果关系。此外，在实际应用中，群体个数往往是未知的，而本文所提出的算法无须指定群体个数。文献［18］考虑的则是二元变量之间的因果关系，在为每个样本识别了因果关系后，基于每个样本所对应的因果关系参数进行K-Means［19］聚类，因此也面临着需要指定群体个数的问题。

2 问题定义

本节对所研究的问题进行符号化定义和说明。定义n个个体的多元时间序列数据集X={X1，X2，…，Xn}，其中第s个个体的多元时间序列数据Xs={，，…，}，且每个个体的变量 数均为m，时间序列长度均为T。将最长的因果关系时间间隔记为k，多元时间序列数据的因果关系表示为k+1个m×m的矩阵{B0，B1，…，Bk}，Bτ[i，j]≠0 表示第t时刻的变量xi(t)受到第t-τ时刻的变量xj(t-τ)的因果影响，且时间间隔为τ，τ∈{0，1，…，k}，其中τ=0时Bτ表示瞬时因果关系，τ＞0时Bτ表示时延因果关系。

本文所考虑的问题是：给定多元时间序列数据集X，如何基于数据背后的因果关系将n个个体划分成c个群体，且c无须人工先验指定，并学习每个群体的因果关系。

3 LEAD 算法

针对所研究问题，本文提出面向多元时间序列的群体因果关系发现算法LEAD。该算法分为2 个阶段：第一阶段是基于因果关系对全体的多元时间序列数据进行个体级别的聚类，将具有相同因果关系的个体聚集成一个群体，并且无须指定群体的个数；第二阶段基于前一阶段的聚类结果，利用每个群体中所有个体的多元时间序列数据进行群体因果关系发现。图1 展示了LEAD 算法的整体框架。

图1 LEAD 算法框架Fig.1 Framework of LEAD algorithm

下面将先讨论如何基于变分推断的方法，利用个体的多元时间序列数据学习该个体背后的因果关系，该方法在LEAD 算法的2 个阶段中都会涉及，随后将对2 个阶段的具体流程进行介绍。

3.1 基于变分推断的个体因果关系发现算法

本文主要考虑变量之间的因果关系服从线性非高斯的情况，并采用函数模型进行建模。第s个个体的多元时间序列数据的生成机制如下：

其中：N(·)表示一个高斯分布。因此，主要的推断任务是估计真实后验分布p(Bs|Xs)。然而直接计算该后验分布十分困难，本小节采用变分推断的技巧，利用一个易于计算的变分分布q(Bs)去近似真实后验分布p(Bs|Xs)。首先给出第s个个体的观测数据Xs的对数似然度：

从上述推导中可以看出，观测数据Xs的对数似然度存在一个下界，当且仅当KL(q(Bs)||p(Bs|Xs))=0时，该下界等式成立。因此，只需要最大化这个下界，就可以找到一个变分分布q(Bs)足够近似真实后验分布p(Bs|Xs)，由此得到以下目标函数：

通过优化变分分布q(Bs)来最大化式（4）即可近似真实后验分布，从而得到第s个个体背后因果关系。

为了计算式（4），对其进行分解如下：

将等式最后的第一项记为Lell(q(Bs)，Xs)，第二项记为Lkl(q，p)，即：

可以看出：Lell(q(Bs)，Xs)是给定变分分布q(Bs)下观测数据Xs的对数似然度的期望；Lkl(q，p)是近似后验分布q(Bs)与先验分布p(Bs)的KL 散度的负数。因此，最大化式（4）意味着最大化观测数据Xs的对数似然度且同时最小化q(Bs)与先验分布的差距。

式（4）的计算可以通过式（6）和式（7）实现，因此，对变分分布q(Bs)做变分推断中常见的平均场假设，即：

下面给出lnp(Xs|Bs)的具体计算方式。由数据的产生机制（式（1））可知：

进一步用混合高斯分布来对噪声项进行建模，即：

对于式（7），先验分布p(Bs)和变分分布q(Bs)都是高斯分布，因此，可以通过解析式直接计算2 个高斯分布的KL 散度。基于上述推导分析，可以对目标函数式（4）进行估计并计算梯度，进而采用梯度上升的方式对变分分布q(Bs)和噪声分布pe(es(t))中的参数进行优化，从而最大化目标函数，得到第s个个体背后的因果关系Bs。

3.2 基于因果关系的聚类算法

上节给出了如何基于变分推断的方法，利用个体的多元时间序列数据学习该个体背后的因果关系，本节将介绍如何基于学习到的个体因果关系进行聚类。

设计聚类算法的目的是为了将具有相同或者相似因果关系的个体聚成一个群体，从而利用群体的数据来学习群体背后的因果关系。因此，本文从因果关系的角度来度量个体之间的相似性并设计个体聚类过程，提出基于因果关系的时间序列聚类算法，如算法1 所示。

算法1基于因果关系的时间序列聚类算法

算法2Split(Cv，Lv)函数算法

算法1 的设计主要借鉴了分裂层次聚类的思想，初始时将全部个体作为一个群体，随机选择一个个体Xs作为群体代表进行因果关系学习，以学习得到的变分分布q(Bs)作为群体共同的因果关系，并计算每个个体在群体因果关系下的似然度（算法第1～7 行）。个体似然度高意味着该个体的因果关系与该个体所在群体对应的群体共同因果关系相似；个体似然度低意味着该个体的因果关系与该个体所在群体对应的群体共同因果关系不相似。随后算法进入循环过程（算法第8～18 行），在每一次循环中，需要从当前已有的群体中选择出群体内部个体似然度方差最大的群体。群体内部个体似然度的方差越大，意味着该群体内部个体的数据背后越可能是不同的因果关系，导致在相同的群体因果关系下，有些个体似然度高，有些个体似然度低。在此基础上，基于选出的群体，利用算法2 对其做分裂，并根据划分前后群体所有个体的似然度之和是否增加来决定是否接受这次分裂，如果总体似然度之和没有增加，则拒绝分裂且跳出循环，此时算法1 返回聚类结果并结束（算法第19 和20 行）。

由于分裂后的2 个群体分别学习各自的因果关系并在对应群体因果关系下计算该群体内的个体的似然度，无法直接比较分裂前后群体方差的变化，同时本文希望个体似然度高，因此算法1 以群体内部的所有个体似然度之和是否增加作为是否分裂的条件。同时，算法1 在拒绝分裂后随即跳出循环结束算法流程具有2 点好处：一方面缓解了经典分裂层次聚类算法需要分裂到单个个体作为一个簇才停止的情况，降低了时间复杂度；另一方面无须为算法指定群体的个数，循环停止时即得到了群体的个数，避免了经典层次聚类算法结束后仍需要选择簇个数的问题。

3.3 群体因果关系发现算法

上节基于因果关系将全部个体划分成了多个群体，并且无须指定群体的个数，本小节将基于前一阶段的聚类结果，利用每个群体中的所有个体的多元时间序列数据进行群体因果关系发现。

本节所提出的群体因果发现算法主要基于贝叶斯思想，即利用数据更新先验分布得到后验分布并循环这一更新过程，算法伪代码如算法3 所示。

算法3群体因果关系发现算法

算法3对于每个群体进行遍历，在同一个群体内，先初始化该群体因果关系的先验分布（算法第2 和3 行），再对该群体内的个体进行遍历，对于一个个体，利用该个体数据对式（4）最大化得到近似后验分布，并以此近似后验分布作为下一次的先验分布，重复这个过程直到所有个体都参与过群体因果关系分布的更新（算法第4 和7 行），以最终得到的近似后验分布的期望作为该群体的群体因果关系并保存结果（算法第8～9 行），直到遍历完所有群体。通过上述步骤就可以学习出各个群体共享的群体因果关系。得益于3.1 节中基于变分推断的个体因果关系发现算法与贝叶斯思想，算法3 能够充分地利用群体内所有个体的数据，并且学习出群体背后的因果关系。

4 实验

为了验证本文提出的LEAD 算法，本节将使用仿真数据和真实数据对算法进行实验评估。

4.1 仿真数据集

设计4 组控制变量实验，具体如下：

1）群体个数c={2，3，4，5，6}，个体总数n=60，个体的时间序列长度T=60，变量个数m=5。

2）群体个数c=2，个体总数n={20，30，40，50，60}，个体的时间序列长度T=60，变量个数m=5。

3）群体个数c=2，个体总数n=30，个体的时间序列长度T={40，60，80，100，120}，变量个数m=5。

4）群体个数c=2，个体总数n=30，个体的时间序列长度T=60，变量个数m={6，8，10，12，14}。

本文所提出的LEAD 算法对多个个体进行聚类并学习个体背后的因果关系（即该个体所在群体的群体因果关系），因此，本节将其与主流聚类算法对比聚类的效果，与时间序列因果发现算法对比因果发现的效果。

聚类对比算法如下：1）K-Means（Euclidean），基于欧氏距离的K-Means 算法［19］；2）K-Means（DTW），基于DTW 距离［22］的K-Means 算法；3）DBSCAN（DTW），基于DTW 距离的DBSCAN 算法［23］；4）OPTICS（DTW），基于DTW 距离的OPTICS 算法［24］。上述聚类对比算法采用Python 包scikit-learn 中的实现方法，参数设置为各算法实现的默认参数。其中，K-Means 算法需要指定簇的个数K，本小节实验将按真实值来指定K，注意K在实际中往往是未知的。

因果关系发现对比算法如下：1）基于约束的PCMCI 算法［8］；2）基于评分的DYNOTEARS 算法［9］；3）基于函数的VAR-LiNGAM 算法［10］。上述时间序列因果发现对比算法均采用官方开源代码实现，并按真实值设置对比算法的最大因果关系时间间隔参数，其余参数采用原算法实现的默认参数。

在评价指标方面，本实验选择ARI（Adjusted Rand Index）指标［25］对聚类算法进行评价，选择AUC（Area Under Curve）指标对因果关系发现算法进行评价。ARI 计算公式为：

其中：n是给定数据集中个体总数；nij是在聚类结果R中属于簇i同时在聚类结果R*中属于簇j的个体数量；ni是在聚类结果R中属于簇i的个体数量；nj是在聚类结果R*中属于簇j的个体数量；

ARI 的取值范围是［-1，1］，随机划分下ARI 为0，ARI 越大说明R和R*结果越一致。AUC 是ROC曲线下的面积，ROC 曲线是以假正率（FPR）为横轴，真正率（TPR）为纵轴，在多个阈值下得到一系列点（FPR，TPR）所构成的曲线，其中FPR 和TPR 计算公式为：

其中：将预测因果结构与实际因果结构相比；FP是预测有边但实际无边的数量；TN是预测无边实际也无边的数量；TP是预测有边实际也有边的数量；FN是预测无边但实际有边的数量，AUC 的取值范围是［0，1］，AUC 越接近1，预测因果结构与真实因果结构越接近。

在仿真实验中，相同参数的实验都在10 个不同随机种子下进行数据生成并运行LEAD 算法和对比算法，分别计算评价指标并取10 次结果的平均值作为算法的最终结果，结果如图2～图5 所示。

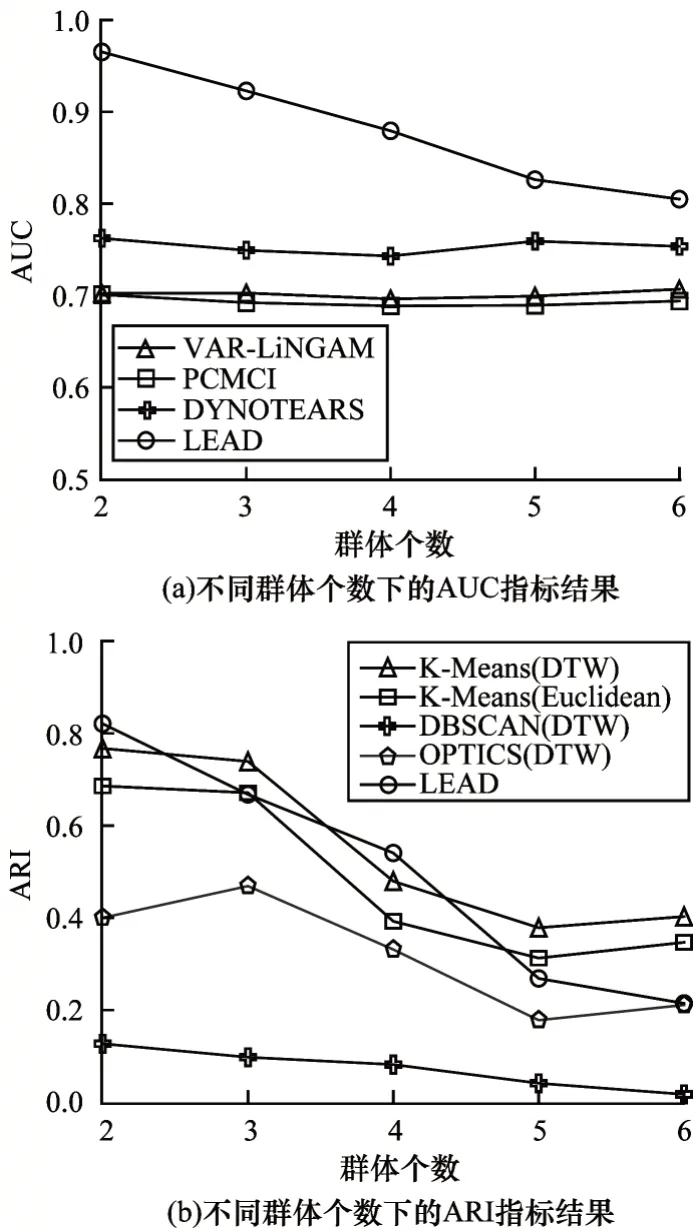
图2 针对群体个数的控制实验Fig.2 Control experiments on the number of groups

图2 显示了个体总数相同但背后群体个数不同情况下的实验结果。可以看出本文提出的LEAD 算法的因果发现效果要优于对比算法。但随着群体个数的增加，LEAD 算法的因果发现效果下降，这是因为实际群体个数越多，聚类的难度会越大，特别是在群体个数未知的情况下难度会更大，因此LEAD 算法第一阶段的聚类效果变差，导致第二阶段的因果发现效果也下降。事实上，图2（b）中的聚类方法都随着群体个数的增加而效果变差，其中K-Means（Euclidean）和K-Means（DTW）由于给定了真实群体个数作为算法参数，因此效果要优于其他方法。而本文提出的LEAD 算法在没有给定真实群体个数的情况下，也取得了相近的聚类效果。

图3 显示了群体个数相同但个体总数不同情况下的实验结果。可以看出LEAD 算法的因果发现能力远高于对比算法，这是因为LEAD 算法可以利用群体内多个个体数据。随着个体总数增加，聚类的难度增大，LEAD 算法的聚类效果有所影响，但其因果发现效果基本没有影响，甚至因为数据增加而略微改善。

图3 针对个体总数的控制实验Fig.3 Control experiments on the total number of individuals

图4 显示了不同时间序列长度下的实验结果。随着序列长度增加，图4 中的因果发现算法和聚类算法效果都有所改善，且LEAD 算法无论是因果发现还是聚类的效果均要优于对比算法，说明LEAD算法不仅具有优异的因果发现能力，而且还具有很好的多元时间序列聚类能力。

图4 针对时间序列长度的控制实验Fig.4 Control experiments on the length of time series

图5显示了不同变量个数下的实验结果。从图5（b）可以看出，随着变量个数增加，个体间的差异信息越来越丰富，聚类的难度会下降，聚类算法的效果均明显改善。但与此同时，变量间的因果关系也更复杂，因果发现的难度增大，因此图5（a）中的因果发现算法均随着变量个数增加而效果变差，但LEAD 算法仍然优于对比算法，验证了算法的有效性。

图5 针对变量个数的控制实验Fig.5 Control experiments on the number of variables

4.2 真实数据集

本节选择在真实的Sachs 数据集［5］进行测试。Sachs 数据集在不同的干预措施下测量了细胞中11种磷酸化蛋白质和磷脂分子的浓度变化，不同干预措施下这11 种分子的因果关系会发生变化［4］，本节使用干预cd3cd28+U0126 和干预cd3cd28+aktinhib下的数据，2 种干预下的数据分别属于2 个群体，并以30 作为一个个体的时间序列长度对数据进行切分，得到每个25 个个体的数据。

将LEAD 算法和聚类算法应用到该数据集中，并展示LEAD 算法所学习出的因果关系。由表1 可以看出，本文提出的LEAD 算法的聚类效果要优于对比算法，因为LEAD 算法能很好地捕捉到因果关系上的变化而其他距离度量方式不容易捕捉到这种变化。进一步分析聚类结果发现，LEAD 算法很好地将属于干预cd3cd28+aktinhib 组的25 个个体划分在同一群体（记为群体a1）中，但是将属于干预cd3cd28+U0126 组的25 个个体分成了2 个群体，其中一个群体（记为群体U1）有21 个个体，另一个群体（记为群体U2）有4 个个体。

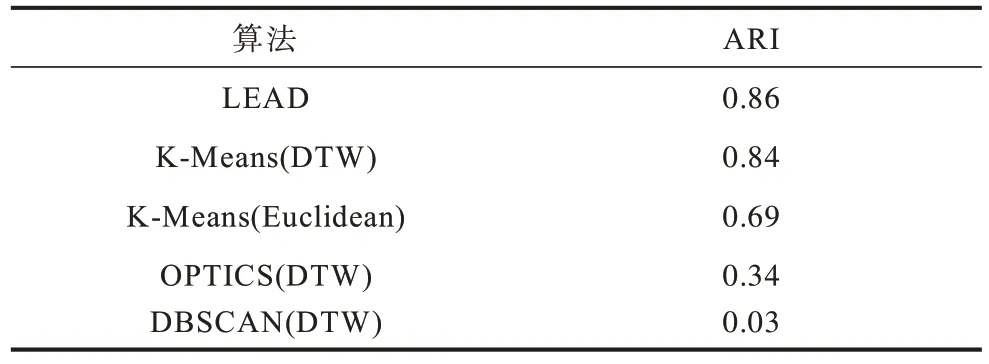
表1 在真实数据集中的聚类性能 Table 1 The clustering performance on real dataset

本文算法学习的因果关系如图6 所示，其中有向边a1 为群体a1 中的因果关系，有向边U1 为群体U1 中的因果关系，有向边U2 为群体U2 中的因果关系，仅显示每个群体中影响权重前十的因果关系。可以看出，群体a1 的重要因果关系与群体U1、群体U2有较大区别，而群体U1、U2的重要因果关系有5条相同，说明算法能够区分在不同干预下的个体。此外，在群体U1、U2 中都发现了因果关系Erk →Akt，该因果关系与文献［5］中报告的一致，但在群体a1 中并未被发现，这是因为在群体a1 中Akt 被干预，从而切断了Akt 的原因变量，验证了算法的有效性。

图6 真实数据集中学习到的3 个群体因果关系Fig.6 Three collective causal relations learned from real dataset

5 结束语

现有因果关系发现方法在多个个体数据背后有相同因果关系的情况下样本利用不足。针对该问题，本文提出一种面向多元时间序列的群体因果发现算法。该算法通过基于因果关系的聚类，将多个个体按照因果关系的相同或不同划分成多个群体，且算法无须指定群体个数。在此基础上，为每个群体通过群体因果发现算法学习群体因果关系。实验结果表明，该算法可以充分利用具有相同因果关系的多个个体数据，因果发现能力优于对比算法，并且同时具有和对比算法相近的多元时间序列聚类能力。本文关注于因果关系是线性的情况，下一步将考虑在因果关系满足非线性的情况下如何进行群体因果发现，进一步提升算法的适用范围。