缜密思维 严谨答题——以一道判断三角形形状的问题为例

林国红

(广东省佛山市乐从中学 528315)

数学的灵活与严谨，时刻体现在知识的运用和解决问题中，若轻视数学的严谨性，往往在解决数学问题时，会导致解答的过程失之严密完整，而产生遗漏甚至错误的结果.下面以一道判断三角形形状的问题为例，说明数学解答严谨的重要性.

1 试题呈现

A.等腰三角形

B.直角三角形

C.等腰三角形或直角三角形

D.等腰直角三角形

2 两个错解

图1

即b(b+c)(c+a-b)=a(a+c)(b+c-a).

化简整理,得(a-b)(a2+b2-c2)=0.

故可得a=b或a2+b2=c2.

所以△ABC是等腰三角形或直角三角形，故选C.

两式相减，得cosA-cosB=sinB-sinA.

即sinA+cosA=sinB+cosB.

两边平方，得1+2sinAcosA=1+2sinBcosB.

即sin2A=sin2B.

从而得2A=2B或2A=π-2B.

所以△ABC是等腰三角形或直角三角形，故选C.

3 错因分析

上述两个解答粗看思路清晰，过程详尽，似乎正确，但其实两个解答的过程不严谨，所得的结论是错误的！错误的原因是由于利用题目两个条件的轮换对称性，导致扩大了解集的范围，从而得出错误的结论.

4 正确的解法探究

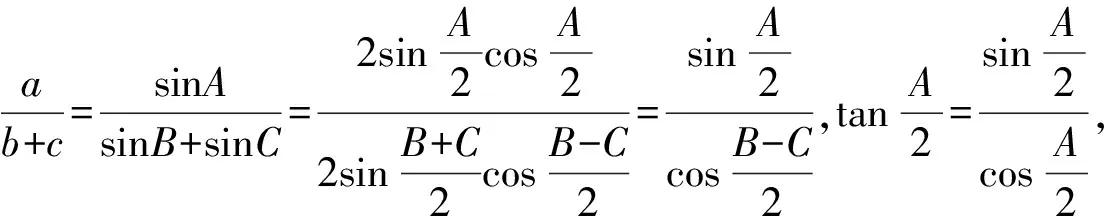
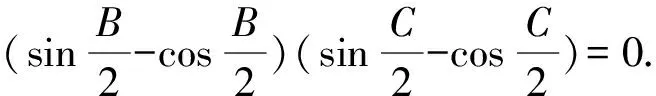
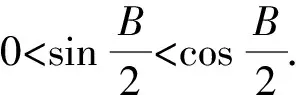
所以△ABC是直角三角形，故选B.

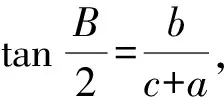
若A=B-C，则B=A+C>|C-A|，与B=|C-A|矛盾，所以A=C-B.

于是由A+B+C=π，得C-B+B+C=π.

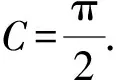
所以△ABC是直角三角形，故选B.

两式相加，得

2(1-sinC)2=2-2sin(A+B)=2-2sinC.

化简整理，得sinC(sinC-1)=0.

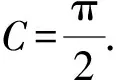
所以△ABC是直角三角形，故选B.

5 两个错解的进一步探究

实际上，错解1与错解2的推理过程并没有错，只是解答不严谨，还没做完，下面将错解1的解答过程补充完整(错解2也可以参照补充完整).

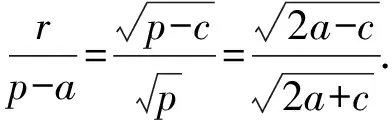
化简,得2a2=c2.即a2+b2=2a2=c2.

故a=b时，△ABC为等腰直角三角形.

(2)当a2+b2=c2时，△ABC是直角三角形.

综合(1)(2)，可知△ABC是直角三角形，故选B.

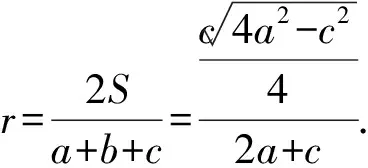
图2

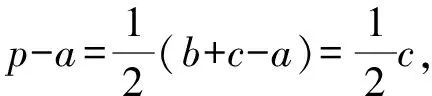
从而有a2+b2=2a2=c2.

故a=b时，△ABC为等腰直角三角形.

(2)当a2+b2=c2时，△ABC是直角三角形.

综合(1)(2)，可知△ABC是直角三角形，故选B.

严谨性是数学学科的基本特点，它不仅要求数学结论的叙述必须精炼、准确，而且对结论的推理论证要求既严格又周密，所以在解题过程中要着重因果关系、条件和结论的联系,缜密思考，注意解答的严谨性，做到不重不漏，经得起推敲.