例析与高斯函数有关问题的常考题型与备考建议
刘海涛
(安徽省芜湖市第一中学 241000)
1 问题的提出
《高考评价体系》指出:高考要从“知识立意”转向“能力立意”,考查学生的“关键能力”和“核心素养”.这就要求学生在学习中,学会灵活运用所学知识分析、解决问题,达到从“解题”向“解决问题”的转变.笔者在一轮复习的教学中,发现高斯函数频频出现在一些数学题中,学生面对此类问题常因方法不当,或运算过程繁杂,导致虽做对但耗时太多,或做错丢分,成绩不理想,而若能熟练掌握高斯函数的定义与性质,将其运用到解题中,定会事半功倍,提高解题正确率与效率.如何帮助学生在高考复习备考中,遇到与高斯函数有关的问题时,能够准确、快速、高效地解答呢?笔者通过梳理,现将该类问题整理成文,与读者交流,以期抛砖引玉.
2 高斯函数的介绍
2.1 高斯函数的定义
设x∈R,用[x]表示不超过x的最大整数,则称y=[x]为高斯函数,也叫取整函数.显然,其定义域为R,值域为Z.高斯函数的定义域是连续的,但值域是离散的.
我们把一个数的小数部分记作{x},则有x=[x]+{x},显然0≤{x}<1.一般地,我们称y={x}为小数函数.
2.2 高斯函数的性质
(1)若x≤y,则[x]≤[y];
(2)[n+x]=n+[x],其中n∈Z;
(3)x-1<[x]≤x<[x]+1;
(4)[x]+[y]≤[x+y];
(5)若x,y≥0,则[xy]≥[x][y];

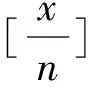
3 例析高斯函数与其他知识的交汇问题
3.1 利用高斯函数解函数问题
3.1.1 求函数解析式
例1 某学校要召开学生代表大会,规定各班每10人推选一名代表,当各班人数除以10的余数大于6时再增选一名代表.那么,各班可推选代表人数y与该班人数x之间的函数关系用高斯函数y=[x]可以表示为( ).


评注该题主要考查学生的逻辑推理能力和综合运用数学知识的能力,另外该题可以用特殊值验证法.
3.1.2 求函数值

解析求导得f′(x)=x2(3lnx+1).
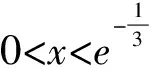
又因为f(e2)=2e6,所以x>e2.



当2
当t>e时h′(t)<0,
所以函数h(t)在(2,e)上单调递增,在(e,+∞)上单调递减.

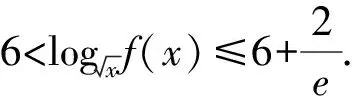
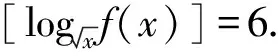
评注该题的难度较大,主要考查利用导数研究函数的单调性与值域,换元法求复合函数值域等,体现了逻辑推理、直观想象、数学运算等数学核心素养.
3.1.3 求函数的值域(或最值)



评注该题属于新定义题,解答的关键在于对定义的理解及变量的分段讨论,这也体现了高斯函数是一种分段函数的属性,考查了学生逻辑推理、数学运算的核心素养.
例4 定义在R上的函数f(x)=[2x]+[4x]+[8x],若A={y|y=f(x),0≤x<1},则A中元素的最大值和最小值之和为____.



故最大值和最小值之和为11.
评注集合A为函数y=f(x)(0≤x<1)的值域,由此问题转化为求函数的最大值与最小值的和,求该函数最值的关键在于,根据高斯函数的定义恰当地分段讨论,该题很好地考查了分类讨论思想.
3.1.4 判断函数的性质
例5 已知函数f(x)=sin[cosx]+cos[sinx],关于f(x)有下列四个结论:
①f(x)的一个周期为2π;
②f(x)是非奇非偶函数;
③f(x)在(0,π)上单调递减;

其中所有结论正确的编号是( ).
A.①②④ B.②④ C.①③ D.①②
解析由f(x+2π)=sin[cos(x+2π)]+cos[sin(x+2π)]=sin[cosx]+cos[sinx]=f(x),得f(x)的一个周期为2π,则编号①正确;
由f(-x)=sin[cos(-x)]+cos[sin(-x)]=sin[cosx]+cos[-sinx],知f(-x)+f(x)=0与f(-x)=f(x)两式均不恒成立,则编号②正确;

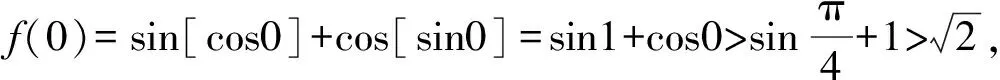
评注该题是一道高斯函数与三角函数结合的判断函数性质的问题,考查了学生的数学运算、逻辑推理等数学核心素养.
3.1.5 函数的零点问题
例6 已知函数f(x)=2x{x}-x-1,则函数的的所有零点之和为( ).
A.-1 B.0 C.1 D.2

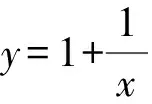
3.2 高斯函数与方程交汇问题


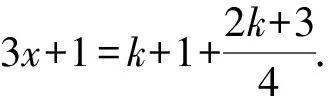


解法2由3x<[3x+1]≤3x+1,得
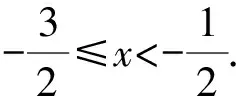
[3x+1]=-1,-2,-3,-4.

综上,方程全部实根和为-2.
评注解答该题的关键在于对高斯函数定义和性质的理解,是一道较简单的方程题,考查了学生的逻辑推理、数学运算核心素养.
3.3 高斯函数与不等式交汇问题
例8 已知x>0,不等式[x]{x} 解析由x=[x]+{x},不等式[x]{x} 所以不等式等价于[x]-1>0. 即[x]>1,即x≥2. 所以不等式解集为[2,+∞). 评注解答该题的关键在于对不等式的合理变形,及高斯函数性质x<[x]+1的运用,考查了逻辑推理、数学运算的数学核心素养. 3.4.1 数列通项问题 解析当x∈[0,1)时,f(x)=[x[x]]=0;当x∈[k,k+1)(k∈N*且k≤n-1)时,x[x]=kx∈[k2,k2+k),则f(x)=k2,k2+1,…,k2+k-1,共有k个取值. 易知当n=13或14时取得最小值为13. 评注解答该题的关键在于抓住高斯函数的定义,将区间进行分段讨论. 3.4.2 数列求和问题 解析当n≥2时,an=(an-an-1)+(an-1-an-2)+…+(a2-a1)+a1=2n+2(n-1)+…+4+3=n2+n+1. 又a1=3满足an=n2+n+1, 所以an=n2+n+1. 例11 已知点集P={(x,y)|[x]2+[y]2=1},则点集P表示的平面区域的面积是____. 易知相应的平面区域为四个边长为1的正方形,故面积和为4. 评注根据高斯函数的定义,逐一表示出平面区域对应的不等式组,便可发现平面区域为4个正方形. 则a+b= 2(2k+1)=4k+2. 所以c2022=[a]=[4k+2-b]=4k+1+[1-b]= 4k+1. 故c2022除以4的余数为1. 《普通高中数学课程标准(2017年版)》指出:在数学高考命题中,考查内容应围绕数学内容主线,聚焦学生对重要数学概念、性质、方法的理解和应用,强调基础性,注重数学本质和通性通法.在高考备考教学中,教师应加强基础知识、基本技能和基本数学思想方法的训练,以达到提高学生数学关键能力和数学核心素养的目的.基于此,笔者提出以下高考备考建议. 通过文中对与高斯函数有关问题的整理发现,该类问题主要考查高斯函数的概念与基本性质,考查的形式主要以选择、填空为主,难度也以中等、容易题为主.因此,我们在复习备考的过程中,要通过对该类试题的研究,归纳总结出高考考查的典型题型及其解题方法,构建完整的知识脉络和方法体系,熟练掌握与高斯函数有关的典型问题的通性通法,形成解题模型.只有扎实掌握了这些通性通法,才能在高考中游刃有余地处理该类问题. 数学思想是对数学知识的本质认识,是数学的精髓,是数学基础知识和数学能力之间的一座“桥梁”.通过上文的梳理,我们发现与高斯函数有关的问题主要考查分类讨论、数形结合、转化与化归等数学思想方法,如文中的例4考查了分类讨论的思想,例6将函数的零点个数转化为两个函数图象的交点个数,考查了转化与化归、数形结合的数学思想.笔者认为复习备考的教学中注重数学思想的渗透,可以帮助学生优化认知结构,学会用数学的眼光观察世界,用数学的思维思考世界,用数学的语言表达世界. 数学学科核心素养的内涵包括数学核心知识、核心能力、核心品质,主要由数学抽象、逻辑推理、数学建模、直观想象、数学运算、数据分析等六个方面组成,这些数学核心素养既有独立性,又相互交融,形成一个有机整体.数学核心素养不是具体的知识和技能,也不是一般意义上的数学能力,它基于数学知识技能,但高于具体的数学知识技能.因此,笔者认为在高考复习备考中,我们广大一线教师不仅要重视解题方法的指导,更要重视对学生核心素养的提高,“授之以鱼不如授之以渔”,学生的数学素养提高了,解题能力和解题效率自然提高,无论高考题型如何变化,也定能在高考中“以不变应万变”,顺利取得高考的胜利.3.4 高斯函数与数列交汇问题

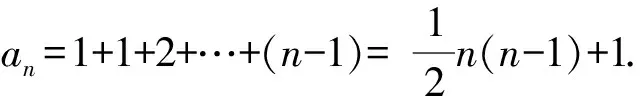




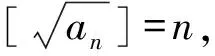
3.5 高斯函数与平面几何交汇问题


3.6 高斯函数与二项式定理交汇问题





4 有关高考复习备考的两点建议
4.1 夯实基本知识,以不变应万变
4.2 渗透思想方法,提高核心素养

