基于同题异构设计“教—学—评”一体化初中数学分层作业

余高霞

【摘要】在初中数学教学中，分层教学是一种有效的教学方法，可以满足不同学生的学习需求.文章以“同题异构”为理论基础，探讨了基于“同題异构”设计“教—学—评”一体化的初中数学分层作业的可行性和有效性.通过对实际案例的设计和实施，收集并分析相关数据，基于优等生、中等生和学困生的不同基础，设计相应的作业形式.不同的作业形式可使不同层次学生达成自己的学习目标，使数学作业分层设计更加科学，从而提升数学作业效果.

【关键词】同题异构；“教—学—评”一体化；初中数学；分层作业

初中阶段学生有着明显的个体差异，如何让不同能力的学生均能通过数学作业提升数学水平是值得研究的问题.“教—学—评”一体化就是实现教学内容、学习内容和考核指标的统一，其对分层作业的实施具有重要意义.

一、案例设计

（一）知识点选择：人教版初中数学八年级上册“三角形全等的判定”

作为初中数学的一部分，“三角形全等的判定”在数学知识体系中占据重要位置.它为学生打下了理解几何学的基础，帮助学生初步掌握几何图形的性质和关系.全等的概念和判定是几何学中最基础和最重要的知识之一.学习“三角形全等的判定”能够帮助学生建立起几何观念，形成对几何图形的认识和直觉感.

（二）样本选择和分层方式

本案例选择八年级某班学生为样本，该班共有46名学生，男生26名，女生20名.该班级在整个八年级中处于中上水平，具有较强的代表性.在分层方式上，本案例依据学生的数学成绩将学生划分为优等生、中等生、学困生三个类别.其中优等生选取班级数学名次前十的学生，学困生选取班级数学名次后十的学生，其他学生归为中等生.

（三）案例目标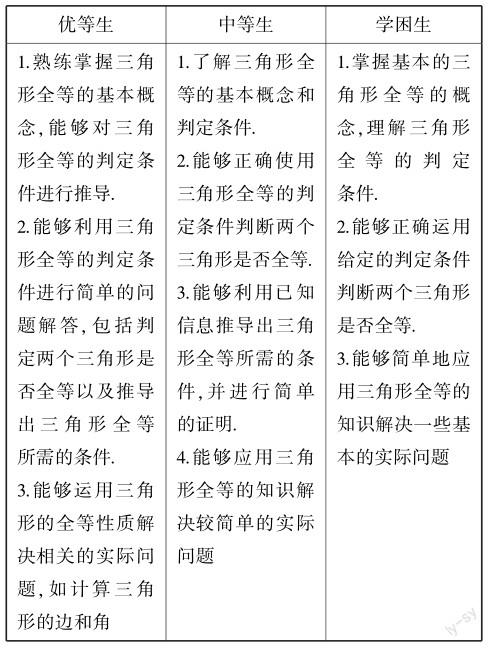

（四）案例流程

1.学生“学”的部分

对于初中数学“三角形全等的判定”这一章节的内容，优等生、中等生和学困生可以采取不同的学习方式，以达到各自的学习目标.

2.教师“教”的部分

在教师讲解知识之前，学生已经通过自学的方式对该章节知识点有了一定的了解.因此，教师在“教”的过程中只需要根据学生的学习情况，开展针对性教学即可.

（1）针对优等生

教师可为优等生提供更高层次的拓展学习资源，如复杂问题、实际应用情境等，以满足他们对知识深入理解和应用的需求.教师可向优等生提供学习案例，鼓励优等生进行独立研究和探究，使之深入思考并提出自己的解决方法，培养其创造性思维能力.教师还可组织学习小组，让优等生之间进行交流，分享学习心得，激发彼此之间的互相学习和竞争意识.

（2）针对中等生

教师可详细讲解三角形全等的基本概念和判定条件，确保中等生能够理解并掌握重点知识.教师可通过实物演示加深中等生对全等三角形的理解.教师还可通过解题示范，演示如何运用判定条件，引导中等生掌握解题思路与技巧.针对中等生的水平，教师可进行差异化教学，根据难易程度分层讲解，并设计不同难度的练习题，帮助中等生逐步提升.

（3）针对学困生

教师可重点讲解三角形全等的基本概念和简易判定条件，帮助学困生建立起扎实的基础.教师可设计相关习题帮助学困生巩固知识记忆和技能运用，帮助其提高解题能力.针对学困生的具体问题和困难，教师还可进行个别辅导和指导，帮助他们理解和解决难点.

此外，教师需要根据学生的学情和学习进度合理安排课堂活动，如小组合作学习、游戏探索等，以激发学生的学习兴趣和积极性.同时，教师需要不断关注学生的学习进展，及时给予反馈和指导，鼓励学生思考和自主学习，促进他们在学习过程中成长和进步.

3.分层作业评价

针对学困生设计了以下基础类题目：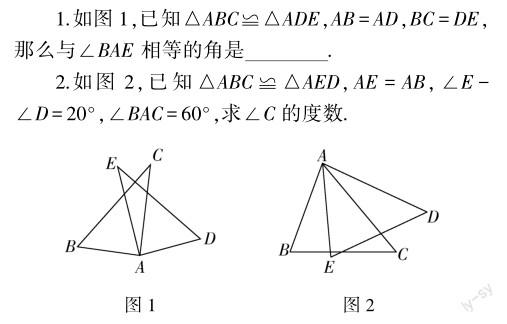

3.如图3，将直角△ABC（其中∠B=34°，∠C=90°）绕A点按顺时针方向旋转到△AB′C′的位置，使得点C，A，B′在同一条直线上，那么旋转角最小等于（ ）.

A.56° B.68° C.124° D.180°

4.如图4，△ACB≌△A′CB′，∠BCB′=30°，则∠ACA′的度数为（ ）.

A.20°B.30°C.35°D.40°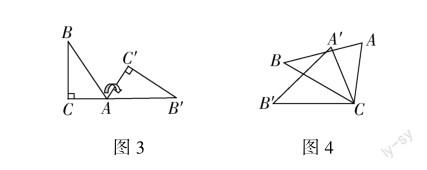

针对中等生设计了以下提高类题目：

1.AD为△ABC中BC边上的中线，若AB=2，AC=4，则AD的范围是（ ）.

A.AD<6B.AD>2

C.2

2.已知在△ABC中，AD平分∠BAC，且∠C=2∠B，求证：AB=AC+CD.

3.如图5，在△ABC中，AB=AC，延长AB到D，使BD=AB，取AB的中点E，连接CD和CE.求证：CD=2CE.

4.如图6，在△ABC中，∠C=2∠B，∠1=∠2.求证：AB=AC+CD.

针对优等生设计了以下挑战类题目：

1.如图7，在锐角三角形ABC中，BE，CF分别是AC，AB边上的高，BE延长至Q，使BQ=CA.在CF上取点P，使CP=BA，分别沿Q和P点向BC作垂线，垂足为O′，P′，求证：PP′+QQ′=BC.

2.P为正方形ABCD对角线BD上任意一点，沿着P点分别向BC和CD上作垂线，垂足为E，F，连接EF，求证：AP=EF.

3.如何利用剪刀、白纸、量角器制作出两个全等三角形？

4.思考生活中的全等三角形应用情况，分析全等三角形在生活中的应用案例.

二、案例结果和讨论

（一）分层作业的设计和实施效果分析

在该案例中通过针对不同层次学生设计分层作业，在很大程度上提升了各层次学生的学习积极性.对于优等生来说，给他们提出了更高难度的挑战，激发了他们的求知欲望和探索能力.对于中等生来说，给他们提供了难度适中的练习和巩固机会.中等生可以在适合自己水平的作业中巩固、掌握基本知识和方法，并逐步提高自己的能力，他们能够在较为自信和舒适的环境下进行学习，可提升学习动力和自信心.对于学困生来说，给他们提供了更低难度的起点，帮助他们逐步掌握基础知识和方法.学困生可以在简单的题目中逐渐建立自信和对数学学习的兴趣，通过小步快跑的方式逐渐迎头赶上.各层次学生作业完成情况如下表所示.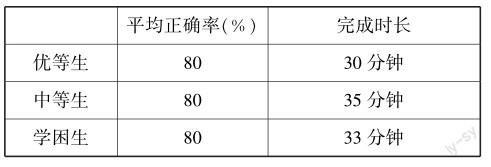

（二）学生对“同题异构”作业的反馈和评价

对于优等生来说，他们对这种作业设计的反馈通常是非常正面的.这是因为对于他们来说统一难度的作业可能无法充分发挥他们的才智和能力.而“同题异构”的作业设计，可以使他们面对更加复杂和有挑战性的问题，促使他们深入思考，提升解题能力，从而获得满足感和成就感.

对于中等生来说，他们通常能够在适宜难度的作业中找到学习动力.这种作业设计能够帮助他们巩固和应用所学的知识，使他们逐步提升解题技巧.中学生在完成这些作业的过程中能够体会到自己的进步和成长，增强数学学习信心.

对于学困生来说，他们常常面临学习上的困难和挫折.“同题异构”的作业设计可以使他们接触到相对简单和入门级的题目，从而巩固基础.这种分层作业设计能够帮助他们建立学习的起点，减少焦虑感，从而激发起他们对数学学习的兴趣.

结 语

在本案例中，首先对学生进行了层次划分，这为科学地开展“教”与“学”奠定了基础.“学”的部分采用了学生自学为主、教师引导为辅的方式，为不同层次的学生提供了丰富的教具，激发了学生的学习热情.“教”的部分根据学生的学习目标不同，采取了不同的形式（异构），优等生的实践环节更多，思维深度也更深，学困生则更加侧重基础.在“评”的环节，主要采用习题作业的方式来检验学生的学习效果，不同层次学生的平均正确率均为80%，说明题目难度设计合理，能够激发不同层次学生的学习热情.因此，教、学、评三个环节处于同一平面上才能够发挥其应有的价值.

【参考文献】

[1]孔佳蕾.基于学生发展的初中数学分层作业设计与实施[J].智力，2023（25）：108-111.

[2]白永潇.核心素养视角下的初中数学分层作业设计[J].新課程教学（电子版），2023（10）：1-3.

[3]任丽莎.基于“双减”政策的初中数学分层作业设计策略研究[J].教学管理与教育研究，2023（9）：71-73.

[4]冯俊，王芳.基于定边对定角模型的同题异构[J].中学数学，2022（2）：75-76.

[5]李大为.同题异构点亮智慧的火花：2011年江苏省初中数学青年教师评优课“圆”的设计亮点评析[J].中学数学杂志，2012（S2）：44-46.