岩石抗剪强度参数的围压效应与定量表征

李 斌，李佳伦，王 鹏，何治良，胡康强，胡芸菡

(1.西南科技大学环境与资源学院，四川 绵阳 621010；2.四川省地质矿产勘查开发局川西北地质队，四川 绵阳 621010)

0 引 言

岩石抗剪强度参数(内聚力c和内摩擦角φ)是岩石工程稳定性分析和设计中的输入信息，该参数通常利用岩石常规三轴压缩强度试验[1]和岩石抗剪强度试验[2]进行测定，这两种试验方法测定岩石抗剪强度参数的理论基础均是Mohr-Coulomb强度准则。大量试验结果表明[3-9]，岩石三轴强度和抗剪强度都具有明显的围压效应：三轴强度-围压关系曲线和抗剪强度-正应力关系曲线均呈上凸的非线性趋势，围压或侧限压力较低时该非线性较弱，可以近似为线性，而随着围压或侧限压力的增加，这种非线性关系明显增强。由于Mohr-Coulomb强度准则是一个线性准则，使得上述试验方法仅在低围压下可以确定唯一的c值和φ值，而在高围压下c值和φ值则会随着围压σ3值的增加发生改变，说明岩石抗剪强度参数在围压的影响下存在一定的不确定性，即岩石抗剪强度参数存在围压效应。在深部岩石工程中，岩石一般处于高地应力环境，且地应力通常存在范围分布，且具有分异性[10-11]。因此，从考虑围压效应的角度研究岩石抗剪强度参数的不确定性对岩石工程可靠度分析具有重要的科学理论意义和实践指导价值。

近年来，岩石抗剪强度参数的不确定性逐渐得到重视，并已取得了较为丰硕的研究成果。岩石抗剪强度参数不确定性研究的首要工作是建立参数样本数据库，目前岩石抗剪强度参数的取值方法有以下几种。李夕兵等[12]和宫凤强等[13]采用排列组合理论选取不同组数的三轴试验数据进行拟合，建立小样本岩石抗剪强度参数信息库；曹文贵等[14]基于非对称三角模糊数确定岩石抗剪强度参数的最可能取值及上限和下限。这两种取值方法存在一个缺点，即没有考虑岩石抗剪强度包络线通常都具有非线性的性质。HOEK等[15-16]、SOFIANOS等[17-18]和ZHANG等[19]根据Hoek-Brown准则推导出等效的抗剪强度参数计算公式；张永杰等[20]和肖欣等[21]采用区间理论根据Hoek-Brown准则计算抗剪强度参数的上限和下限；YANG等[22]、CHOO等[23]和ONG等[24]根据幂函数形式的抗剪强度公式计算出某一侧向压力下的切向峰值凝聚力和切线峰值摩擦角。这些方法考虑了包络线的非线性，而计算参数的可靠性由强度准则的精度决定，因此所选准则的适用性需要验证，如Hoek-Brown准则已证明不适用于表征高应力下岩石三轴强度的非线性特征[25]。

本文从考虑围压效应的角度研究岩石抗剪强度参数的不确定性问题，分析围压对内聚力和内摩擦角的影响，探讨岩石抗剪强度参数的围压效应特征及其表征方法，并以文献[3]中山口大理石为例，构建基于非线性准则优选的岩石抗剪强度参数表征模型，验证提出表征方法的合理性及该方法获取岩石抗剪强度参数的可靠性。

1 Mohr-Coulomb强度准则

Mohr-Coulomb强度准则是室内岩石力学试验测定抗剪强度参数的理论基础，该准则认为岩石抗剪强度τ等于岩石内聚力c与剪切面上法向应力σn产生的摩擦力之和，具体表达式见式(1)。

|τ|=c+σntanφ

(1)

该准则也可用主应力的形式表达，见式(2)。

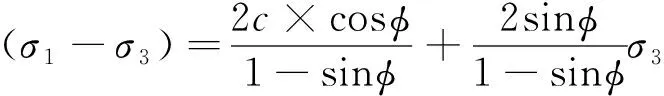
(2)

式中，σ1和σ3分别为岩石破坏时对应的最大主应力和最小主应力。

通过室内岩石常规三轴压缩强度试验测定抗剪强度参数时，理想状态下的抗剪强度包络线如图1所示，以三个莫尔圆为例，图中括号外的数据为莫尔圆编号，括号内的数据分别为对应莫尔圆上的最小主应力和最大主应力。根据试验获取的多组(σ3，σ1)数据，画出系列莫尔圆，并做出斜直线包络线，进而得到内聚力c和内摩擦角φ，也可以将多组(σ3，σ1)数据代入式(2)中，通过线性拟合计算确定内聚力c和内摩擦角φ。

2 岩石抗剪强度参数的围压效应特征

由Mohr-Coulomb强度准则可知，仅选择两组莫尔圆就可以确定对应的一组(c，φ)值。如按围压由低到高的顺序，依次选择相邻的两组莫尔圆，则可以获取多组(c，φ)值，进而可以分析围压对岩石抗剪强度参数的影响。基于客观公正的原则，以文献[3]中的山口大理石为例进行分析说明，具体的三轴压缩试验数据见表1。

图1 理想状态下的抗剪强度包络线Fig.1 Shear strength envelope in ideal state

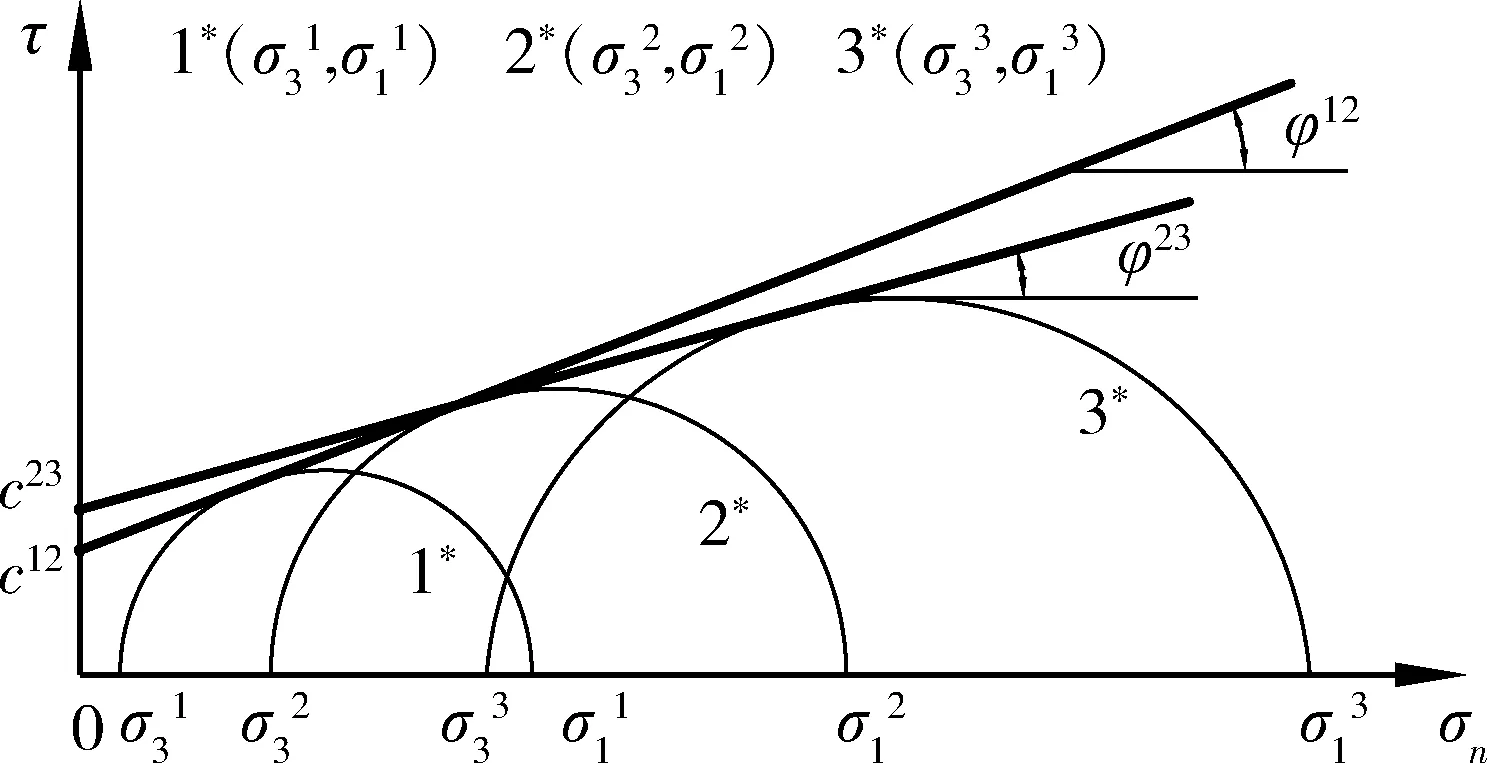
图2 考虑围压效应的抗剪强度包络线Fig.2 Shear strength envelope considering the confining pressure effect

表1 山口大理石三轴压缩试验数据Table 1 Triaxial compression test data of Yamaguchi marble

由表1可知，仅需要选择相邻围压下的两组三轴试验数据就可以确定对应的一组(c，φ)值，因此不需采用最小二乘法进行线性回归处理。具体方式为将相邻围压下的两组三轴试验数据(σ3，σ1)代入式(2)中，建立两个一元二次方程，直接计算得到该围压区间的一组(c，φ)值。 表1中共11组(σ3，σ1)数据，按上述方式可得到10组(c，φ)值，具体结果见表2。

由表2可知，该岩石的抗剪强度参数在不同的围压区间存在较大差异，内聚力和内摩擦角的变异系数分别为0.54和0.55。为进一步分析岩石抗剪强度参数的围压效应特征，以(σ3L+σ3R)/2的简单处理方式得到各区间的中点围压值，通过计算得到内聚力和内摩擦角与区间中点围压的相关系数分别为0.95和-0.89。说明内聚力与围压呈正相关，而内摩擦角与围压则呈负相关，表2中数据也体现出内聚力和内摩擦角随围压的增加整体上分别呈逐渐增大和减小的趋势。

3 考虑围压效应的岩石抗剪强度参数表征方法

针对岩石抗剪强度参数的围压效应，本文提出以瞬态内聚力cinst和瞬态内摩擦角φinst来表示在某一应力状态(σ1，σ3)下的岩石抗剪强度参数。在该应力状态下，岩石抗剪强度包络线和莫尔圆的几何关系如图3所示。σ1和σ3分别为岩石常规三轴压缩强度试验中的最大主应力和最小主应力；τ和σn分别为岩石抗剪强度和有效正应力；φinst为该应力状态下的瞬态内摩擦角。

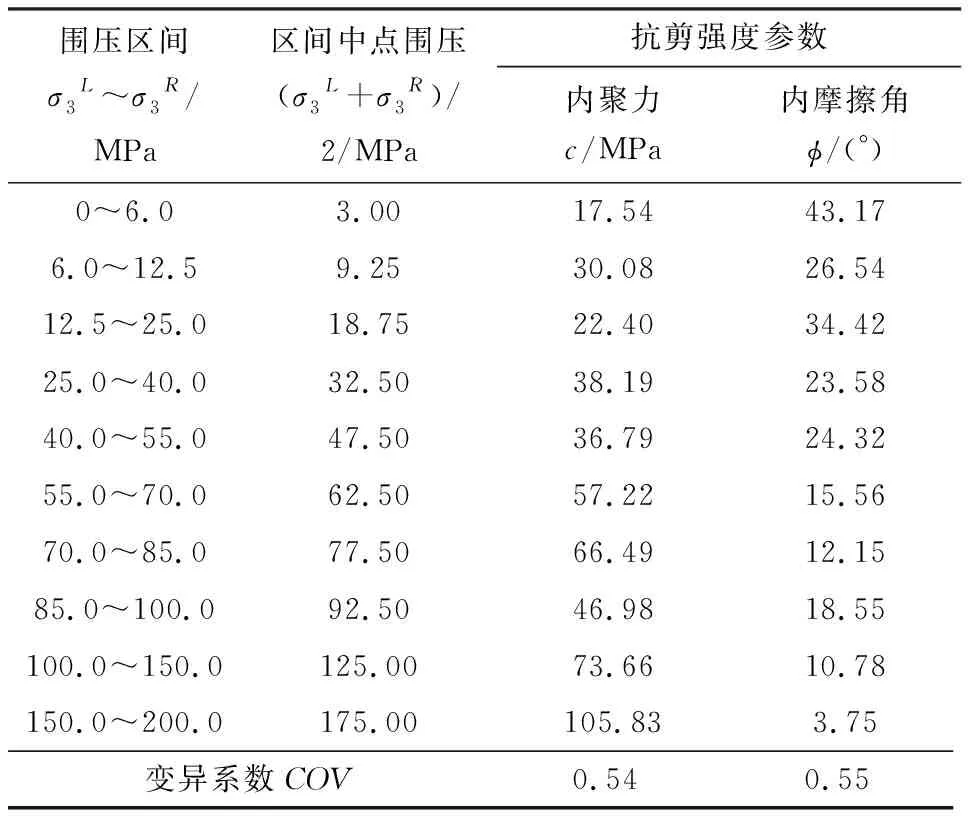
表2 山口大理石在不同围压区间时的抗剪强度参数Table 2 Shear strength parameters of Yamaguchi marble in different confining pressure sections

图3 抗剪强度包络线几何图Fig.3 Geometry of shear strength envelope

图3中A点为该应力状态下包络线与莫尔圆的切点，由直角三角形AHM可知，该点处的正应力和剪应力满足式(3)。

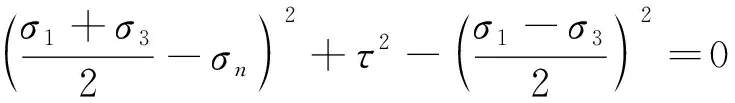
(3)

式(3)对σ3展开求导，可得到σn见式(4)。

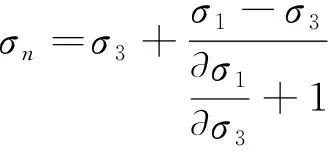
(4)

将式(4)代入式(3)，可得到τ见式(5)。

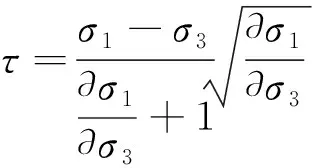
(5)

因此，A点处的切线梯度可表示为式(6)。

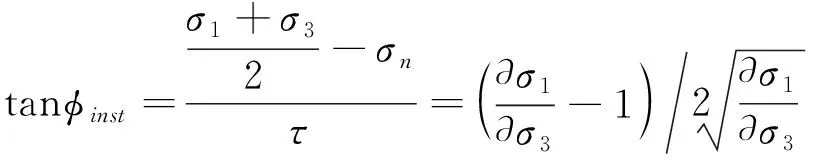
(6)

将式(4)～式(6)代入式(1)即可得到该应力状态下瞬态内聚力cinst的定量表征公式。同时，对式(6)进行反正切函数计算即可得到瞬态内摩擦角φinst的定量表征公式。

由以上推导分析可知，cinst和φinst的定量表征公式由∂σ1/∂σ3决定，而∂σ1/∂σ3可通过岩石强度准则公式f(σ1,σ3)对σ3展开求导得到。因此，岩石强度准则的精度将直接影响到岩石抗剪强度参数表征公式的准确性。

因此，以表1中山口大理石的三轴压缩试验数据为例，开展多种岩石强度准则评估岩石三轴强度精度的对比分析。

4 基于精度评价的岩石强度准则优选

在构造岩石强度准则参数估计的目标函数时，设定自变量(围压σ3)无测量误差，而因变量(三轴强度σ1)存在测量误差。则岩石强度准则用隐函数可表示为式(7)。

(7)

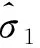
(8)

针对岩石三轴强度的围压效应特征，目前国内外学者已提出众多不同类型的非线性岩石强度准则。本文挑选出两种经典岩石强度准则(Hoek-Brown准则[26]和幂函数准则[27])、两种近期提出的准则(指数型准则[28]和岩石非线性破坏强度准则[29])和两种常见的准则(I-HB准则[25]和M-C准则修正一般表达式[30])进行准则优选分析。这六种准则按照式(7)改写的隐式表达式及通过最小二乘法确定的各准则针对山口大理石的最优参数见表3。由表3可知，含四个参数的准则A4、准则A5和准则A6的拟合优度最高，且基本相等，其次为含三个参数的准则A3和准则A2，含两个参数的准则A1的拟合优度最低。

表3 岩石强度准则的隐式表达式及其最优准则参数Table 3 Implicit forms of the rock strength criteria and there optimal parameters

续表3

为进一步定量比较各准则评估山口大理石三轴强度的精度，下面选取平均相对误差MRE作为评价指标来开展岩石强度准则的优选。根据平均相对误差MRE的定义，该指标可表示为式(9)。

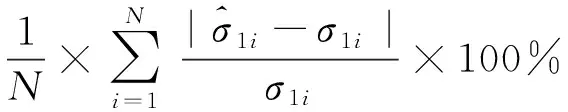
(9)

式中：REi为准则在第i组三轴试验围压时评估的岩石三轴强度的相对误差；N为岩石三轴试验的组数，根据表1中山口大理石三轴试验的组数，N=11。

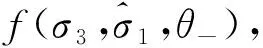
相对误差RE表征的是针对某点的评估值与实际值的偏差，该值越小，准则在某一围压时评估的岩石三轴强度与试验强度就越接近。表4中加*标记的数据为在某一围压时各相对误差RE中的最小值，在共计11组围压条件下，最多组数(六组)的最小相对误差RE归属准则A6。

平均相对误差MRE表征的是针对点序列的评估值与实际值的整体偏差，该值越小，准则评估的岩石三轴强度与试验强度的平均整体偏差就越小，则准则的精度就越高。由表4可知，四参数准则A4、准则A5和准则A6的MRE值均低于三参数准则A2和准则A3，而双参数准则A1的MRE值最高，表明岩石强度准则包含的参数越多，其评估岩石三轴强度的精度就越高。进一步比较四参数准则的MRE值可知，准则A6评估山口大理石三轴强度的精度略高于准则A4和准则A5。

准则在评估不同类型岩石的三轴强度时，其精度一般会存在差异，如准则A在评估岩石Ⅰ的三轴强度时，其精度高于准则B，而在评估岩石Ⅱ时则可能会反之。本文研究重点不在于论证岩石强度准则之间的优劣，而是在于分析如何科学合理地决策出一种适用于某一具体类型岩石的高精度岩石强度准则。因此，鉴于岩石强度准则的精度直接影响到岩石抗剪强度参数表征公式的准确性，选取准则A6来开展山口大理石抗剪强度参数的定量表征分析。

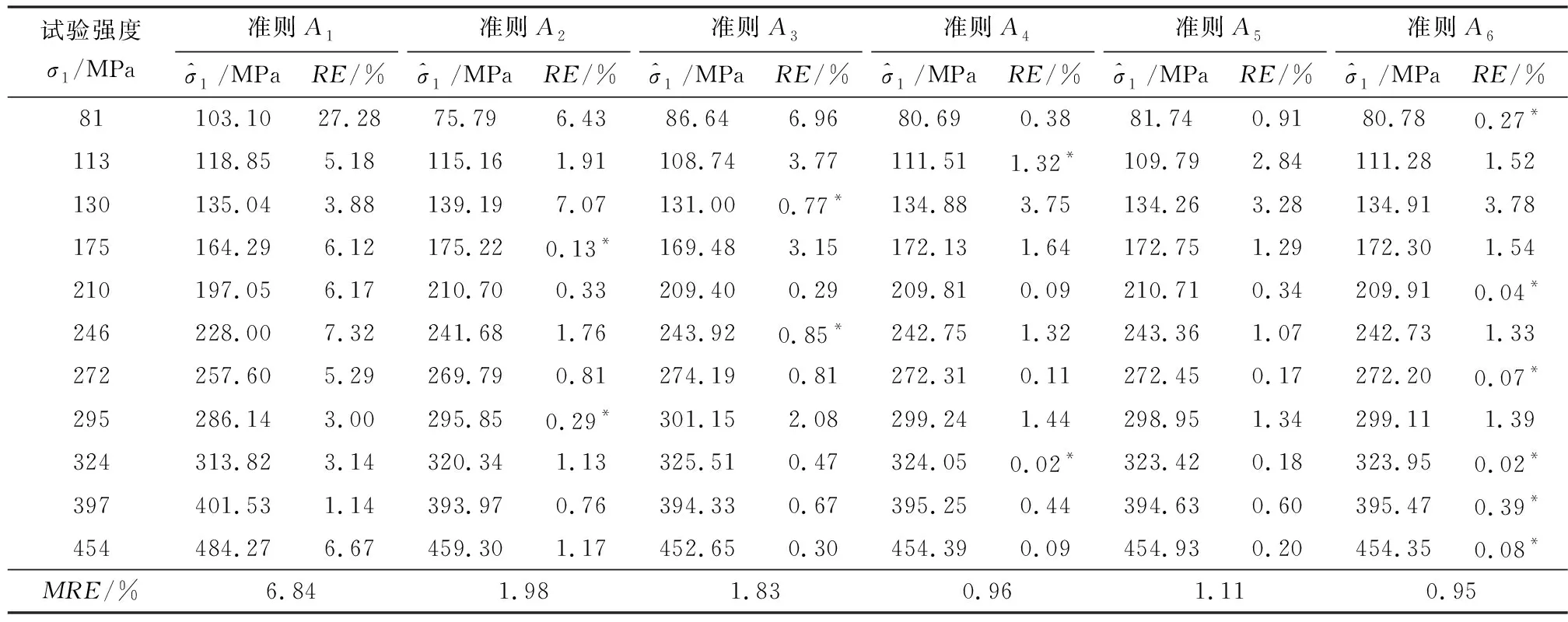
表4 岩石强度准则对山口大理石三轴强度的评估结果Table 4 Evaluation results of triaxial strength of Yamaguchi marble by the rock strength criteria

5 印证分析

5.1 山口大理石抗剪强度参数表征模型

为验证考虑围压效应的岩石抗剪强度参数表征方法的合理性，以山口大理石为例开展印证分析。表3中准则A6的显式表达式见式(10)。

(10)

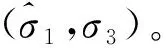
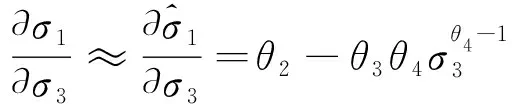
(11)

将式(11)代入式(6)，即可得到瞬态内摩擦角φinst的表征公式见式(12)。

(12)

(14)

将式(12)～式(14)代入式(1)，即可得到瞬态内聚力cinst的表征公式见式(15)。

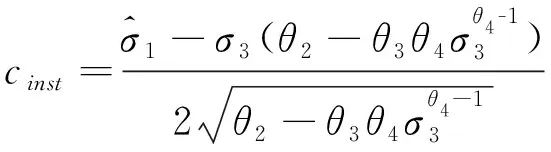
(15)

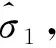
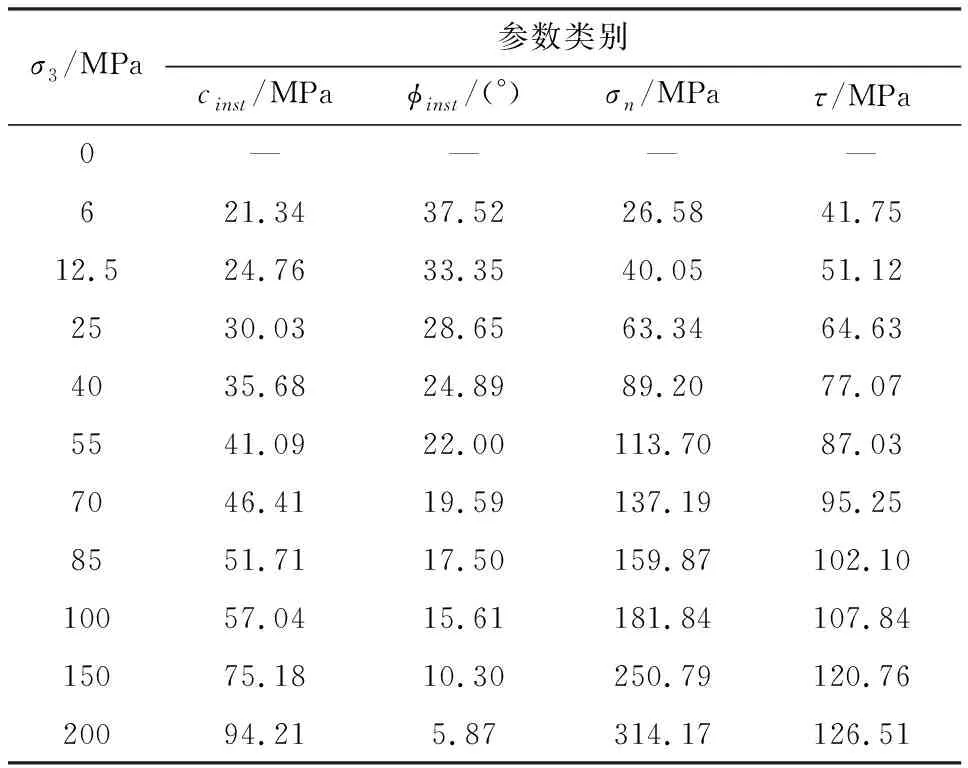
表5 山口大理石的瞬态参数值Table 5 Instantaneous parameters of Yamaguchi marble

5.2 合理性分析

由表5可知，山口大理石的瞬态内聚力cinst和瞬态内摩擦角φinst随围压σ3的增大分别呈现出增大和减小的变化规律。这些规律与表2中山口大理石抗剪强度参数在不同围压区间时的试验值的变化趋势相吻合，符合岩石抗剪强度参数的围压效应特征。

为进一步分析，根据表1中三轴试验数据及表5中的应力组合点(σn，τ)，在τ-σ坐标系下分别绘制莫尔圆及抗剪强度包络线如图4所示。其中，括号外的数字为莫尔圆编号，括号内的数据分别为对应莫尔圆上的最小主应力σ3和最大主应力σ1，方形点标记为各应力组合点，用光滑曲线连接各点得到由表征方法确定的抗剪强度包络线。

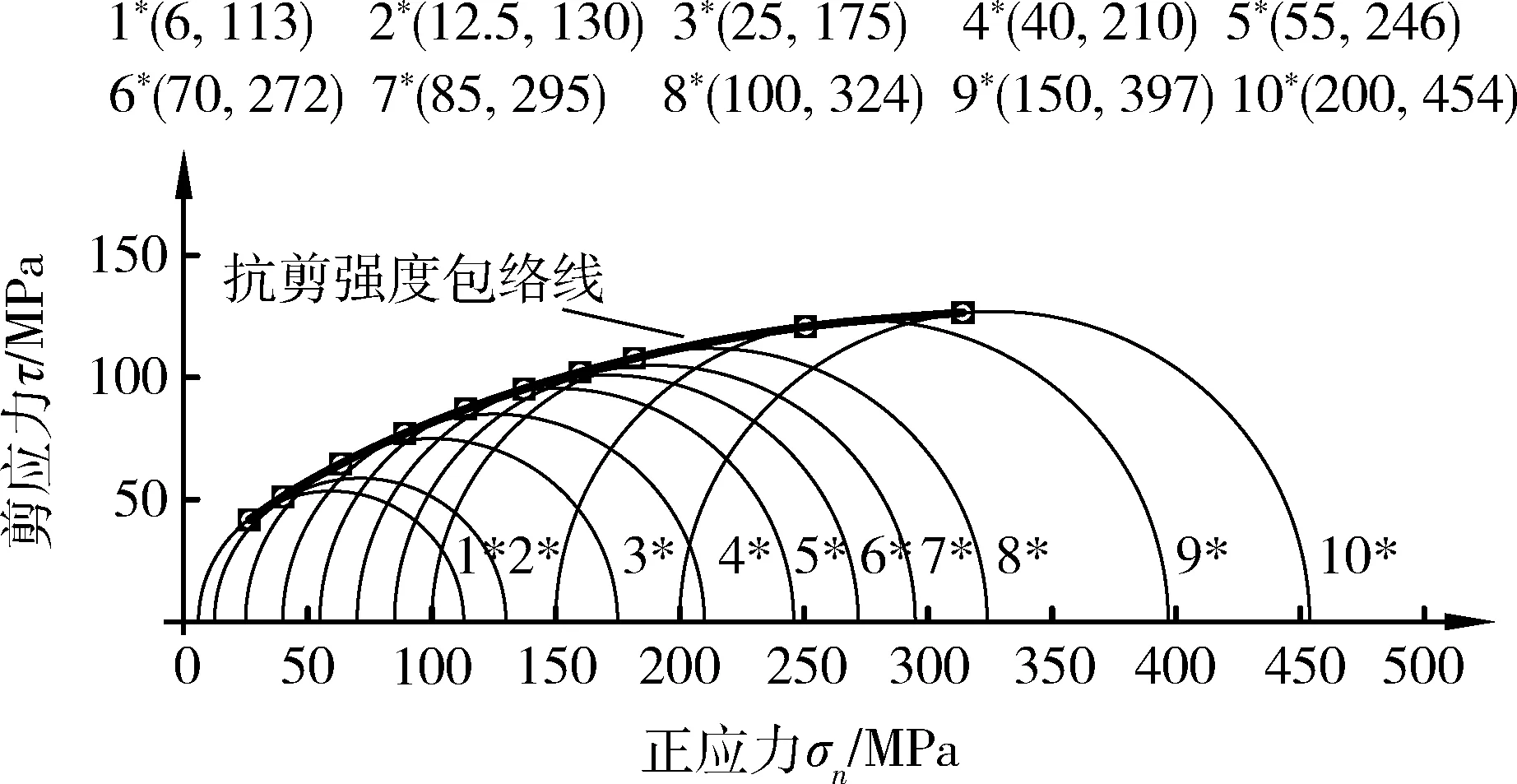
图4 山口大理石抗剪强度包络线Fig.4 Shear strength envelope of Yamaguchi marble

由图4可以直观地观察到该抗剪强度包络线符合岩石抗剪强度的围压效应特征，且与各莫尔圆基本保持相切状态，说明式(13)、式(14)能够较好地表征岩石在应力状态(σ1，σ3)下的抗剪强度。由于包络线上各点的切线与τ轴的交点为对应应力状态下的cinst，切线斜率为对应应力状态下的tanφinst，因此可以间接证实所提出瞬态抗剪强度参数表征方法的合理性。

5.3 可靠性分析

为分析表征方法获取的瞬态抗剪强度参数的可靠性，将其与试验结果(表2)进行比较(由于内聚力可由内摩擦角根据Mohr-Coulomb准则得到，因此这里只分析内摩擦角)。理想的抗剪强度包络线应与各莫尔圆精准相切，由拉格朗日中值定理可知，该理想包络线在两个莫尔圆之间必定存在一点，使得该点处的切线斜率等于这两个莫尔圆外公切线的斜率。这两个莫尔圆外公切线的斜率即为根据对应的两组三轴试验数据计算得到的tanφ，即在围压区间σ3L～σ3R得到的试验φ值，在理想包络线上必定存在一点(该点处围压大于σ3L小于σ3R)，使得该点处的切线斜率等于tanφ(采用φ(σ3L～σ3R)表示该点对应的内摩擦角)。根据抗剪强度-正应力关系曲线呈上凸的围压效应特征及连续性可得到，理想包络线在围压等于σ3时的内摩擦角应该落在φ(σ3L1～σ3R1)和φ(σ3L2～σ3R2)之间，其中，σ3L1<σ3R1=σ3=σ3L2<σ3R2。

对比表5和表2可知，有七组围压σ3(分别为6 MPa、12.5 MPa、25 MPa、55 MPa、85 MPa、100 MPa和150 MPa)时的瞬态内摩擦角均落在对应的φ(σ3L1～σ3R1)和φ(σ3L2～σ3R2)之间。 如σ3为6 MPa时，φinst=37.52°，φ(σ3L1～σ3R1)可取φ(0～6)=43.17°，φ(σ3L2～σ3R2)可取φ(6～12.5)=26.54°，得到φ(6～12.5)<φinst<φ(0～6)；而围压为40 MPa、70 MPa时则出现异常，究其原因是准则在该段围压时评估的三轴强度与试验强度存在的偏差，因此岩石强度准则精度越高则该异常出现的概率就越小。

通过以上分析可知，可判据在大多数情况下是满足的，说明用表征方法获取的瞬态抗剪强度参数代替理想包络线上的抗剪强度参数具有可靠性。

6 结 论

1) 基于岩石三轴强度和抗剪强度的围压效应特征，提出岩石抗剪强度参数具有围压效应，并以山口大理石为例分析围压对岩石抗剪强度参数的影响，揭示其围压效应特征，即内聚力与围压呈正相关，而内摩擦角与围压则呈负相关。

2) 根据莫尔圆和抗剪强度包络线的几何关系，结合Mohr-Coulomb准则进行推导，提出一种考虑围压效应的岩石抗剪强度参数表征方法。同时，以山口大理石为例，开展基于精度评价的岩石强度准则优选，建立基于非线性准则的岩石抗剪强度参数表征模型，并验证了表征方法的合理性及该方法获取瞬态抗剪强度参数的可靠性。

3) 提出的岩石抗剪强度参数定量表征方法可以计算大批量围压下的瞬态内聚力和瞬态内摩擦角，为后续的参数边缘分布和参数间的联合分布研究提供大样本数据库。