路矩阵相关谱半径和路谱展的界及其应用

卢鹏丽， 栾睿

(兰州理工大学 计算机与通信学院，甘肃 兰州 730050)

1 基本概念和主要引理

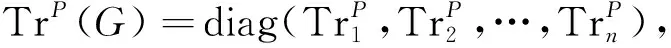
引理2[14]n阶连通图G只有2个不同的路特征值当且仅当G是k-连通且k-正则图，2≤k≤n-1。

引理3[15]设Q为对应于方阵A的等价划分的商矩阵，则A的谱包含Q的谱。

2 图的路谱半径和路无符号拉普拉斯谱半径的界

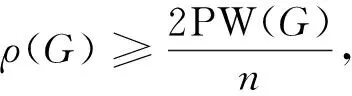
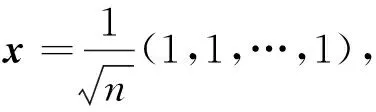
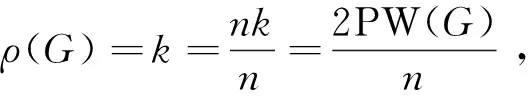
等式成立当且仅当G为路传递正则图。

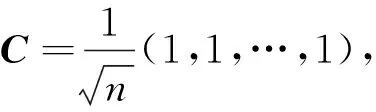
定理3若G为简单连通图，则：

等式成立当且仅当G为路传递正则图。

证明：因为PQ(G)=TrP(G)+P(G)，通过简单计算可得

则

rvi((PQ(G))2)=rvi((TrP)2+TrPP+PTrP+P2)=

rvi(TrP(TrP+P))+rvi(PTrP)+rvi(P2)=

定理4若G为简单连通图，则：

等式成立当且仅当G为路传递正则图。

证明：证明过程同定理3。

(1)

等式成立当且仅当G为路传递正则图。

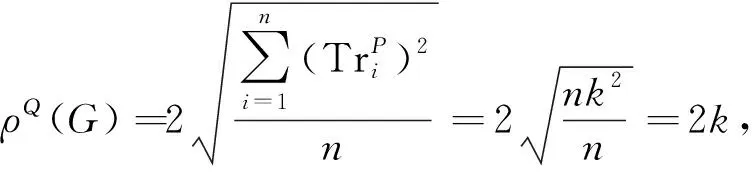
3 路谱展的下界

定理6设图G为n阶连通图，则：

(2)

等式成立当且仅当G为k-连通且k-正则图。

当且仅当ρ2=ρ3=…=ρn时式(2)取等，即当且仅当G有2个完全不同的路特征值。利用引理2，可以得出G为k-连通且k-正则图。反之，若G为k-连通且k-正则图，可通过直接计算可证。该定理得证。

定理7设图G为n阶连通图，则：

等式成立当且仅当G为k-连通且k-正则图。

证明：因为

(3)

当且仅当ρ2=ρ3=…=ρn时式(3)取等，即当且仅当G有2个完全不同的路特征值。利用引理2，可以得出G是k-连通且k-正则图。反之，若G为k-连通且k-正则图，可通过直接计算可证。该定理得证。

推论1设图G为n阶连通图，其路Wiener指数为PW(G)，则：

PS(G)≥

等式成立当且仅当G为k-连通且k-正则图。

证明：根据定理1和定理7可证。

定理8设图G为n阶连通图，则：

4 完全r-部图的路谱和路(无符号)拉普拉斯谱

SpecP(Kp1,p2,…,pr)=((p1-n)p1-1,(p2-n)p2-1,…,

(pr-n)pr-1,1,2,…,n)

的特征值。

证明：给顶点集V(Kp1,p2,…,pr)一个划分π:V(Kp1,p2,…,pr)=V1∪V2∪…∪Vr，其中Vi为第i部中的顶点，则完全r-部图Kp1,p2,…,pr的路矩阵P(Kp1,p2,…,pr)的分块矩阵表示为：

则这个矩阵的n-r个特征值为：(p1-n)p1-1,(p2-n)p2-1,…,(pr-n)pr-1。因为π为图Kp1,p2,…,pr的路等价划分，所以其对应的商矩阵Q3由式(4)给出，计算det(xI-Q3)，可得Q3的特征值，由引理3可知，即为P(Kp1,p2,…,pr)的剩余r个特征值。

推论2令Kp,p,…,p为特殊的完全r-部图，其中r≥2，n=rp，则 SpecP(Kp,p,…,p)=((p-n)n-1,((n-p)(n-1))1)，PE(Kp,p,…,p)=2(n-p)(n-1)。

证明：根据定理9可证。

其中ζ1,ζ2,…,ζr为矩阵

的特征值。

证明：

其中：

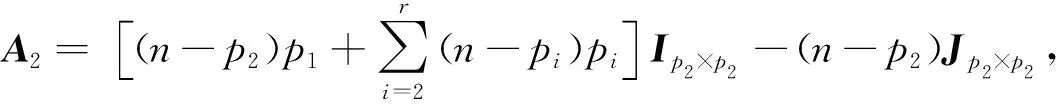
(n-p3)Jp3×p3，…，

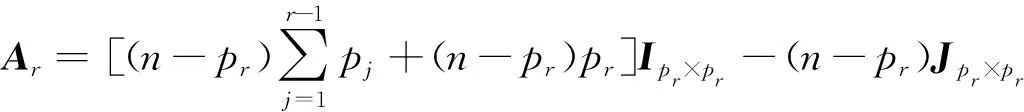
证明过程同定理9。

推论3令Kp,p,…,p为特殊的完全r-部图，其中r≥2，n=rp，则 SpecPL(Kp,p,…,p)=((n(n-p))n-1,0)，PLE(Kp,p,…,p)=2(n-p) ·(n-1)。

证明：根据定理10可证。

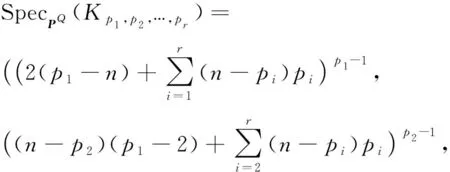
其中ξ1,ξ2,…,ξr为矩阵

的特征值。

其中：

⋮

证明：

其中：

⋮

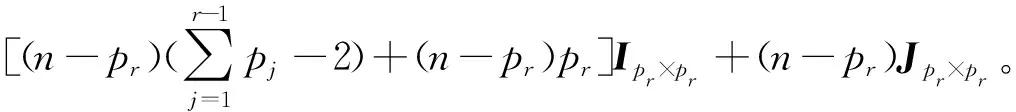
证明过程同定理9。

推论4令Kp,p,…,p为特殊的完全r-部图，其中r≥2，n=rp，则 SpecPQ(Kp,p,…,p)=(((n-2)(n-p))n-1,(2(n-1)(n-p))1)，PSLE(Kp,p,…,p)=2(n-p)(n-1)。

证明：根据定理11可证。

5 结论

1)得到了任意图的路谱半径和路(无符号)拉普拉斯谱半径的界。

2)定义了路谱展的概念并得到其下界。

3)计算了完全r-部图的路谱和路(无符号)拉普拉斯谱及其能量，拓宽了路谱的研究范围。