大开口船型波浪弯/扭矩间接监测方法

范鑫杨， 李辉， 张猛， 曲先强

(1.哈尔滨工程大学 烟台研究院，山东 烟台 264000；2.广东海装海上风电研究中心有限公司，广东 湛江 524000)

由于非大开口船型的抗扭刚度非常大，波浪扭矩对船体结构的影响较小，在非大开口船型波浪力矩间接监测时忽略了扭矩的影响。但对于集装箱船等大开口船型而言，船体抗扭刚度较低，其所承受的波浪扭矩作用不可忽略[1]。

结构载荷的间接监测，即载荷识别，是结构力学中的反问题。载荷识别问题的研究源于20世纪70年代的航空领域[2]，通过监测得到的结构响应反求飞机所受的外部动态载荷。从20世纪末，载荷识别技术逐渐应用到船舶结构载荷的间接监测中[3-4]。张猛等[5]提出了一种Tikhonov正则法与粒子群优化算法相结合的混合算法用于闸门冰载荷的反演，识别出了冰载荷的近似分布。Ritch等[6]对加拿大海岸警卫队的破冰船的局部冰载荷进行了间接监测研究，通过监测得到的结构响应反求船体外板承受的分布式冰载荷。许劲松[7]提出了一种时域估测方法，从耦合的升沉，纵摇测量数据间接监测出船体垂向波浪弯矩值。梁文彬[8]研究了光纤光栅船舶结构健康监测系统的整体方案，并用双光纤光栅实现了船体梁弯矩载荷的间接检测。

Choi等[9]提出了一种在集装箱船中部安装长基线应变仪的船体应力监测系统的应变分解方法，该方法用线性矩阵方程表示，分解后的应变向量等于变换矩阵的逆与实测应变向量的乘积。通过在实际集装箱船上的应用，证明是一种有效的求解集装箱船弯扭力矩的方法。但该分解算法为半经验半解析法，算法表达式简单，缺乏理论依据。

由于大开口船型船体弯/扭联合的复杂性，监测船体单一横剖面特定位置的结构纵向应变很难准确计算出监测横剖面所承受的波浪弯矩与波浪扭矩，本文提出了一种联合双剖面监测法，其数学模型基本形式通过结构弯/扭分析得到，计算精度通过全船有限元仿真验证。

1 波浪弯/扭矩间接监测的数学模型

船舶在实际运营中或在海上航行时，其所承受的波浪弯/扭矩一般在船中附近最大，所以在监测波浪弯/扭矩时LVDT长基线应变仪一般布置在船中附近，其监测到的结构响应是2 m范围内的结构平均微应变，对局部载荷不敏感，能更准确得到纵向应变。LVDT长基线应变仪监测到的结构纵向应变成分极其复杂，在监测船体波浪弯/扭矩时假定LVDT长基线应变仪监测到的结构纵向应变仅由波浪弯/扭矩引起。此外，船体扭矩一般包含2种成分，即自由扭转扭矩和二次扭矩。在波浪弯/扭矩与结构纵向应变之间建立完整的映射关系之前需要明确各外力矩与结构纵向应变之间的关系。

1.1 总纵弯矩与结构纵向应变之间的关系

如图1所示，在大开口船体舱段内安装4支长基线应变仪LBSG_A、LBSG_B、LBSG_C和LBSG_D，其在局部坐标系下的坐标分别为(yA,zA)、(yB,zB)、(yC,zC)和(yD,zD)。局部坐标系的原点与结构横剖面的形心位置相同，如图1所示。在此定义，能使船体结构向上拱起，即向Z轴正向拱起的总纵弯矩MV为正，反之为负。

图1 长基线应变仪布置Fig.1 Arrangement of long base strain gauges

若此船体舱段仅承受总纵弯矩MV的作用，由纯弯曲假定，很容易得到总纵弯矩MV与4支长基线应变仪安装位置处的结构纵向应变之间的线性关系：

(1)

式中：E为弹性模量；Iy为船体横剖面对Y轴的惯性矩。

1.2 横向弯矩与结构纵向应变之间的关系

在此定义，能使船体结构向左舷拱起，即向Y轴正向拱起的横向弯矩MH为正，反之为负。若此船体舱段仅承受横向弯矩MH的作用，由纯弯曲假定，很容易得到横向弯矩MH与4支长基线应变仪安装位置处的结构纵向应变之间的线性关系：

(2)

式中Iz为船体横剖面对Z轴的惯性矩。

1.3 自由扭转扭矩与结构纵向应变之间的关系

自由扭转也称为圣.维南扭转，即结构在扭转过程纵向应变不受约束。根据结构剖面形式，结构剖面可分为开口、闭口以及混合等3种主要结构形式。集装箱船等大开口船型一般为多闭口结构。由于正多边形结构在扭转过程中横剖面没有翘曲正应力，即正多边形结构所承受的扭矩仅含有自由扭转扭矩一种成分，所以为简要说明自由扭转扭矩与结构纵向应变之间的关系，以圆筒形结构的扭转为例，如图2所示。

图2 结构自由扭转Fig.2 Structural free torsion

图2所示的圆筒形结构右端刚性固定，左端仅有扭矩Tf作用。圆筒形结构横剖面的扭心(扭转中心)与其形心重合，如图2中的O点。长基线应变仪通过基座安装与A、B2点，用于测量圆筒形结构外表面的一条纵向“纤维”AB的长度变化量。在扭矩Tf作用前，AB的长度为L，扭矩Tf作用后，B点变化至B′，AB′的长度变为L′，左端剖面扭角为φ，扭转半径，即长基线应变仪距扭转中心的直线距离为r。所以，长基线应变仪的监测应变可表示为：

(3)

进而得到：

(4)

船体结构的纵向应变一般可认为是微量，所以：

(5)

最终，自由扭转扭矩与纵向应变之间的关系可表示为：

(6)

式中：G为剪切模量；J为结构横剖面自由扭转惯性矩。

类似，若船体舱段仅承受自由扭转作用，如图3所示。大开口船型的横剖面扭心一般位于船体基线以下，如图3中的O点。4支长基线应变仪与扭心O的直线距离分别为rA、rB、rC和rD，则自由扭转扭矩Tf与结构纵向应变之间的关系可表示为：

图3 船体结构自由扭转Fig.3 Free torsion of hull structure

(7)

1.4 二次扭矩与结构纵向应变之间的关系

船体扭矩一般为自由扭转扭矩和二次扭矩的和，其在大开口货舱区的近似分布如图4所示。

图4 船体扭矩成分Fig.4 Component of hull torque

二次扭矩Tω为双力矩B的导数，即:

(8)

二次扭矩Tω和双力矩B在大开口货舱区的近似分布如图5所示。

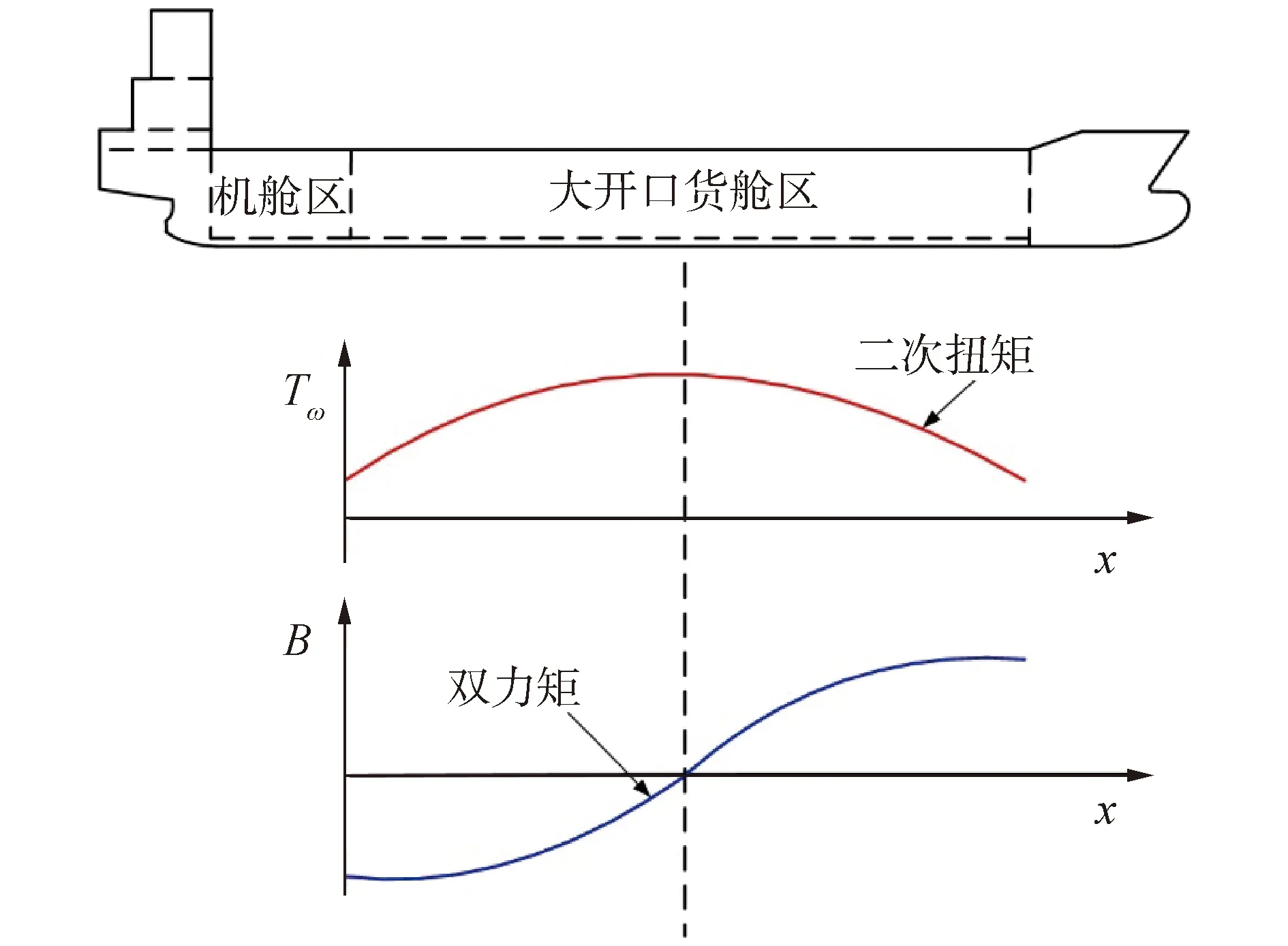
图5 双力矩与二次扭矩Fig.5 Bimoment and warping torque

若大开口舱段仅受二次扭矩Tω作用，二次扭矩Tω与长基线应变仪安装位置处的结构纵向应变并无线性关系，而双力矩B与结构纵向应变存在线性关系：

(9)

式中：ε为长基线应变仪安装位置处的结构纵向翘曲应变；ω为长基线应变仪安装位置处结构扇性坐标；Iω为船体结构横剖面的扇性惯性矩。

1.5 波浪弯/扭矩间接监测的数学模型

若某一大开口舱段同时承受总纵弯矩MV、横向弯矩MH、自由扭转扭矩Tf和双力矩B的作用，则传感器安装位置处的结构纵向应变可由线性叠加得到：

ε4×1=K4×4·f4×1

(10)

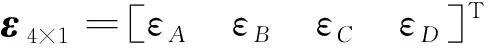
(11)

明显，式(10)是一个静定数学模型，即已知物理量和未知物理量的数量相同。为提高监测结果的精度和稳定性，长基线应变仪的合理数量一般做上浮50%～100%的处理。考虑成本和精度问题，在船体监测横剖面内安装6支长基线应变仪，则数学模型可以表示为：

(12)

综上所述，单一船体横剖面监测的数学模型可简化表示为：

εn×1=Kn×4.f4×1

(13)

综上可知，长基线应变仪安装位置处的结构纵向应变向量εn×1可通过监测得到，传递矩阵Kn×4可根据力学原理逐一计算各元素得到。在已知εn×1和Kn×4的情况下，外力矩向量f4×1可由直接求逆法或Moore-Penrose逆法得到。但是，外力矩向量f4×1中不包含二次扭矩Tω，进而无法得到船体监测横剖面的扭矩大小。二次扭矩Tω为双力矩B的斜率或导数，所以可通过联合双剖面监测近似得到二次扭矩Tω。联合双剖面监测是指对两个邻近的船体剖面进行监测，然后用两监测横剖面的计算结果近似逼近中间剖面的外力矩结果，如图6所示。

图6 联合双剖面监测Fig.6 Structural monitoring in double section

若在邻近的2个监测横剖面内各布置6支长基线应变仪，则监测横剖面的数学模型可简化表示为：

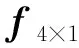
(14)

监测横剖面的外力矩向量为：

(15)

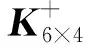
(16)

将式(15)代入式(16)得：

(17)

式(17)为联合双剖面监测的数学模型，得到f4×1之后即可近似得到中间剖面的总纵弯矩MV、横向弯矩MH和扭矩T=Tf+Tω。

大开口船型(如集装箱船)横剖面的扇性坐标的分布形式一般如图7所示，即关于船体横剖面对称线对称。明显，此类大开口横剖面一般存在6个扇性坐标零点。双力矩引起的结构纵向应变可表示为ε=Bω/EIω。所以，在扇性坐标零点处，即ω=0时，双力矩不会引起结构纵向应变。因而，长基线应变仪或其他监测船体纵向应变的传感器安装时应避开扇性坐标零点，尽量安装在扇性坐标值较大的位置，如舷侧上部、顶部以及舭部等位置。

图7 横剖面扇性坐标Fig.7 Fan-shaped coordinate of hull section

2 某集装箱船简化模型

船舶水动力模型如图8所示，其中入射波方向间隔为45°。

图8 船舶水动力模型Fig.8 hydrodynamic model of ship

船舶水动力模型的单元总数为33 729，其中湿表面单元数，即水线面以下的单元数为21 442。船体结构有限元模型如图9所示。

图9 船体结构有限元模型Fig.9 Finite element model of hull structure

频域波浪载荷计算时，频率范围为0.02～0.3 Hz，平均内插69个频率点，共计71个频率点，计算结果如图10所示。图10所示为波浪入射角为45°，频率为0.104 Hz，相位角为-38.9°，波幅为2.5 m的计算结果。

图10 水动力计算结果Fig.10 Hydrodynamic results

对应某入射波方向、频率、相位角和波高的船体湿表面的波浪面压力可由AQWA-WAVE模块导出，然后在经典ANSYS中加载到结构湿表面并计算结构响应。由于水动力模型和结构有限元模型的单元不一致，所以波浪载荷通过映射方式加载，如图11所示。

图11 波浪载荷加载Fig.11 Loading of wave load

3 弯/扭矩间接监测方法的有限元仿真验证

在弯/扭矩间接监测方法的有限元仿真验证中，假定长基线应变仪的安装位置如图12所示。长基线应变仪关于船体中纵剖面对称设置，所以在每个监测横剖面内安装6支长基线应变仪。

图12 长基线应变仪安装Fig.12 Arrangement of long base strain gauges

图12所示的传感器布置方案所对应的数学模型如式(17)所示。式(17)中的剖面惯性矩Iy和Iz、自由扭转惯性矩J、扇性惯性矩Iω、横剖面扭心坐标等可由COMPASS软件直接计算出，进而可得到长基线应变仪与扭心的距离rA～rF。但是，长基线应变仪安装位置处的扇性坐标值ωA～ωF需要通过数值法另行计算。

得到数学模型之后，其反求精度的验证过程与波浪弯矩间接监测的验证过程一致。此外，大开口船型在斜浪航行时所承受的波浪扭矩几乎达到最大，故在验证数学模型反求结果精度时仅以斜浪航行为例，即波浪入射角为45°。2 m波高时的波浪弯/扭矩反求结果如图13所示。

图13 波浪入射角β为45°时间接监测结果(2 m波高)Fig.13 Indirect monitoring results when wave incident angle is β=45°(2 m wave height)

由图13可看出，波高2 m时，总纵弯矩MV和横向弯矩MH的反求结果精度较高，总纵弯矩MV峰值误差约在5%，横向弯矩MH峰值误差约在9%。但是，扭矩T的反求结果误差较大，峰值误差约在30%。4 m波高时，波浪弯/扭矩反求结果如图14所示。

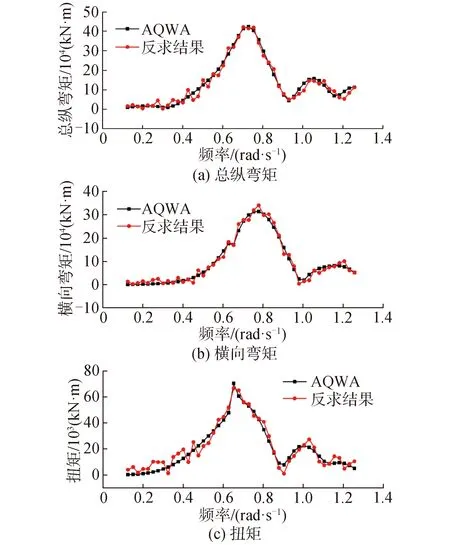
图14 波浪入射角β为45°时的间接监测结果(4 m波高)Fig.14 Indirect monitoring results when wave incident angle is β=45° (4 m wave heigh)

从图14中可以看出，波高4 m时，总纵弯矩MV和横向弯矩MH的反求结果精度较高，总纵弯矩MV峰值误差约在2%，横向弯矩MH峰值误差约在9%。此外，扭矩T的反求结果的精度基本可以接受，峰值误差约在6%。对比波高2 m和波高4 m的反求结果可看出，载荷较大时反求精度一般较高，载荷较小时反求精度一般较低。

4 结论

1) 大开口船型斜浪中航行时易受波浪扭矩作用且大开口船型抗扭刚度偏低，针对此特点，基于船体扭转基本原理提出了一种根据船体结构纵向应变反求监测横剖面波浪弯/扭矩的方法，即联合双剖面监测法。

3) 通过有限元仿真算例验证了联合双剖面监测法的有效性，结果表明，联合双剖面监测法基本能够准确地反求出波浪弯/扭矩，尤其是载荷较大时。