面向轨道维护的可变轨距轨道模型与钢轨点云的配准方法

陈 丞，张同刚，李 涛，沈 迅，邓 川，金国清

(1.西南交通大学 地球科学与环境工程学院，四川 成都 611756；2.中国铁路上海局集团有限公司 淮安高铁基础设施段， 上海 200071；3.中国中铁二院工程集团有限责任公司 测绘工程设计研究院，四川 成都 610031；4.中铁隧道集团三处有限公司，广东 深圳 518000；5.中铁第五勘察设计院集团有限公司 测绘与地理信息研究所， 北京 102600)

我国目前开通的普速铁路网运营里程已超过10万 km，轨道维护的工作量十分巨大，轨道维护的关键是获得准确的轨道测量数据[1]。现在工务部门的轨道测量工作主要依赖人工通过轨道检测小车在天窗时间内现场测量的方法开展，效率低，难以满足大规模路网维护的需求。车载三维激光扫描(Mobile Laser Scanning，MLS)具有采集数据速度快，能在较短时间内快速获取完整轨道场景的点云数据的技术优势，随着近年来相关软硬件的发展，所获取的三维点云的精度已可满足普速铁路的轨道维护测量的需求，有望成为替代传统人工地面轨道测量的技术手段，其中核心的问题就是从点云中获得准确的钢轨的空间位置。

根据车载MLS点云获取轨道左右钢轨的空间位置主要有两大步骤：①从点云提取完整的钢轨点云，尤其是轨道参数定义所在的钢轨轨头部分点云。针对该问题目前不同学者已提出了多种有效的钢轨提取算法[2-4]。②根据钢轨点云确定钢轨轨顶中心的空间位置，这是轨道测量工作中最核心的成果，获得了左右钢轨的轨顶中心位置、轨距等参数后，可推算超高、轨道平顺性等多项指标。目前研究多关注建模或中线提取，根据提取的钢轨点云来分段确定轨道的空间位置后采用一定的拟合方法来建立整个线路的模型[2]或中线[3,5]。对于如何从钢轨点云中提取轨道维护所需要的各项轨道参数的研究很少，这是是车载激光扫描技术在工务轨道维护中应用的核心问题。

由于点云是离散分布的，直接根据点云来确定轨顶中心位置和轨距等参数存在一定的难度，由于一条铁路的钢轨类型是一致的，其形状具有明确的定义，因而一般思路都是通过首先建立轨道模型或钢轨模型，然后分段将模型与点云进行配准，以配准后模型的位置作为实际钢轨的位置。

Oude等[6]根据钢轨轨脚、轨顶、轨腰、轨距等几个参数构建一个粗略钢轨模型，然后分别与左右钢轨点云采用MCMC方法[7-8]进行配准，确定点云中的轨道位置，建立轨道模型；然后在此基础上提出了固定轨距的双钢轨轨道模型[3]，解决了配准后左右钢轨不平行的问题。由于其采用的模型较为粗略，限制了其定位精度，另外模型轨距是固定不变的，这与实际运营铁路线路的情况不符。由曲线段存在轨距加宽等因素的影响，对一条线路而言，轨距并非固定不变。

由于一条铁路线路的钢轨类型是完全一致的，钢轨截面形状和尺寸也是已知的，因此可建立精确的模型，然后利用迭代最小距离(Iterative Closest Point, ICP)[9-10]或其扩展算法[11-12]将其与实际钢轨点云进行配准，可以有效提高轨道参数的获取精度。Soni等[13]利用两台地面激光扫描仪来获取钢轨点云，然后根据钢轨参数建立准确钢轨模型，将其分别于左右钢轨的完整点云[13]或点云中轨顶、轨腰和轨脚等平面部分[14]采用ICP方法进行配准，获得了轨道位置。由于运营线路的轨腰和轨脚部分表面不光洁，还可能附着弹条扣压等其他物体。如要精确滤除钢轨本体之外的其他物体，难度较高且消耗很多预处理时间；否则对最终结果存在一定的不利影响。

为获取精确的钢轨位置和轨距等关键的轨道参数，本文提出了面向轨道维护的可变轨距轨道模型与钢轨点云的配准方法，首先根据实际钢轨截面形状制作一个附加轨距调整因子的双钢轨轨道模型，然后分段采用稳健的ICP方法与钢轨点云进行配准，进而获取左右钢轨的位置和实际轨距等轨道几何参数。采用3 km长的实际运营干线铁路的车载点云数据对算法性能进行了测试，并对基于单钢轨轨道模型、固定轨距双钢轨模型和顾及轨距偏差轨道模型的配准方法进行了对比分析，实验结果基于可变轨距轨道模型的配准精度为0.16 mm，并能准确获取轨距参数。

1 基于钢轨点云的轨道几何参数测量方法

1.1 轨道模型

考虑到铁路线路中存在直线段和曲线段两种情况。当线路长度L=1 m时，按我国干线铁路最小曲线半径(r=500 m)推算，曲线矢高ΔH=0.25 mm，小于钢轨点云的自身精度；曲线半径越大，矢高ΔH值越小。对于干线铁路而言，轨道长度L=1 m时，无论位于曲线段还是直线段，均可将其视为直线。因而在建立局部钢轨模型时，可不再区分直线段和曲线段。左右钢轨的断面形状参数按照标准来设置，本文采用CHN60钢轨断面。

与文献[13]研究类似，首先根据我国规范中的铁路钢轨截面参数建立钢轨模型，称为“单钢轨轨道模型”；然后将2个单钢轨轨道模型按照标准轨的轨距g0=1 435 mm组合构建轨道模型，称为“固定轨距轨道模型”。再此基础上，考虑到轨距的变化，增加一个轨距调整因子(Δg)，称为“可变轨距轨道模型”(见图1)。模型长度均设置1 m。

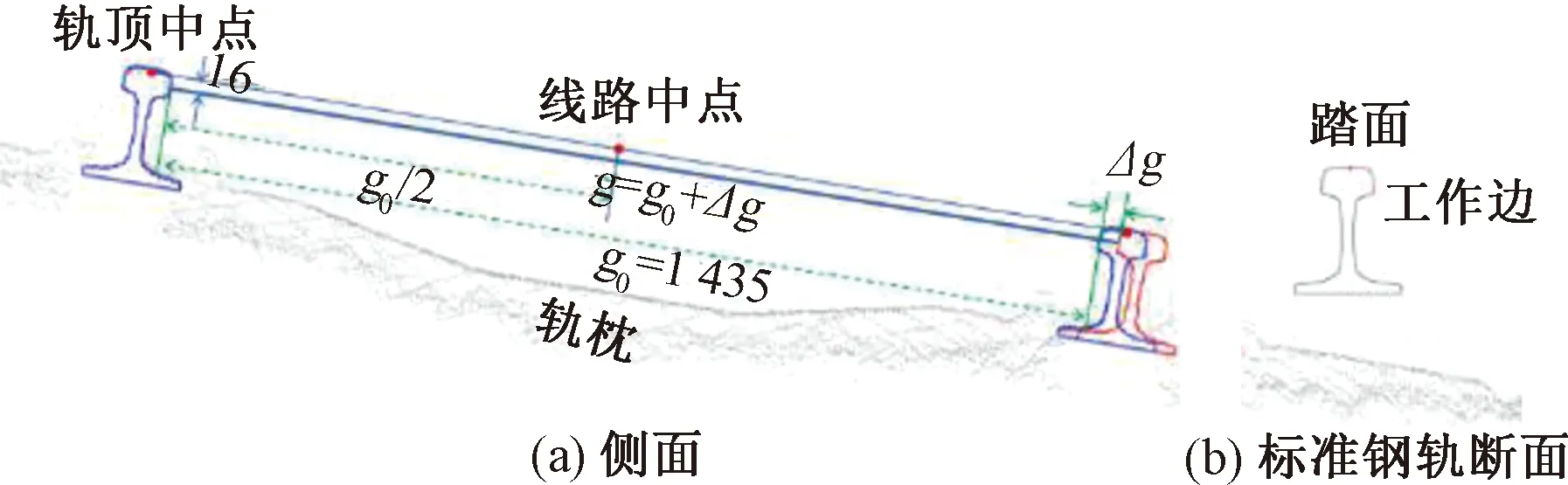
图1 可变轨距轨道模型(单位：mm)

为了方便后续确定轨道参数和配准，还需在模型中的左右钢轨模型的踏面、工作边等2个部分以及轨顶中心和轨面下16 mm处等水平和轨距的定义点进行标记。

1.2 轨道模型与钢轨点云配准算法

首先将钢轨点云按里程方向分为长度L的小段，然后将轨道模型与小段的钢轨点云进行配准，以获取每一段的轨道参数。

对于单钢轨轨道模型和固定轨距的轨道模型，按照文献[13]直接采用ICP配准完成模型与点云的配准。

对于可变轨距轨道模型与钢轨点云配准本文提出的算法流程见图2。

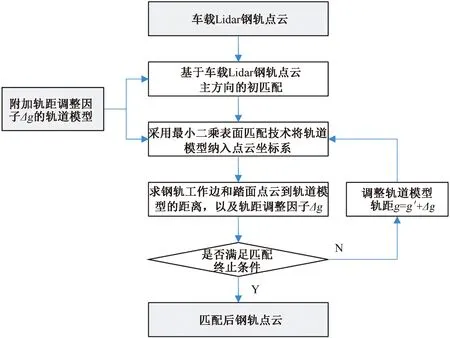
图2 可变轨距轨道模型与钢轨点云配准算法流程

可变轨距轨道模型配准算法过程如下：

Step1基于PCA方法[15]完成轨道模型与钢轨点云的初配准，确定轨道模型的初始位置和姿态。

Step2按照欧氏距离最小准则建立轨道模型与车载Lidar钢轨点云的对应关系，采用ICP算法原理迭代求解配准参数，并对模型进行旋转平移。

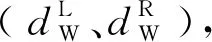
Step4若满足配准终止条件，配准完成；否则调整轨道模型，使得模型轨距g=g′+Δg，重复Step3～Step4。

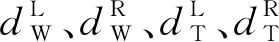
配准过程中只用钢轨轨部分的踏面和工作边点云。钢轨踏面和工作边由于经常与车轮相互接触，其表面光滑、不会附着任何杂物；踏面和工作边会定期打磨，其形状与理论形状的一致度很高；更重要的是钢轨位置、轨距、水平等轨道几何参数都定义在这里。轨腰和轨脚部分表面不光洁，还可能附着其他物体，可能会给最终配准精度带来负面影响。

如轨道模型轨距与钢轨点云的真实轨距一致，在配准完成后，理论上轨道模型与左右钢轨点云在工作边处的距离应为0；如果二者轨距不一致，点云工作边处距离将不为0，其差值反映轨道模型的轨距偏差，据此可以确定轨距变化因子Δg。通过该轨距变化因子可以使得在配准过程中，模型轨距与实际轨距的一致，进而使得配准后的轨道模型能够精确反映点云中轨道的实际位置和姿态。

算法在配准过程中，轨道模型是作为一个刚体处理的，在配准过程中轨道模型的姿态变化不会影响到其内部两根钢轨的相对平行的空间拓扑关系。每次配准完成后，根据工作边上模型与点云的距离偏差对模型轨距进行调整，使得模型轨距与实际轨距逐渐一致，因而能够同步获得实际轨距和精确配准参数。精确配准后轨道模型的左右钢轨反映轨道点云中钢轨的实际空间位置。

由于铁路的纵坡和曲线段的超高是通过道床和道砟来实现，存在纵坡或曲线超高的轨道与平面轨道相比，仅存在整体空间姿态上的差异，左右钢轨的相对空间拓扑关系是一致的，对配准没有影响。

对于双线铁路，由于搭载扫描仪的列车在左线或右线运行，该线左右钢轨的踏面和工作边点云是完整的。而对于其他线，因为钢轨自身遮挡导致邻近的一条钢轨的工作边点云缺失。所以双线铁路需要在左右线分别扫描一次。

1.3 配准过程中轨距调整

左右钢轨上这些距离的计算方法相同，下面以左钢轨为例来给出这些距离的详细说明。假定左钢轨点云上点Pi与模型上Mi是配准过程中建立对应点对，vi是模型上Mi处的单位法向量，指向模型外侧，那么，Pi与Mi的距离可表示为

di(Pi,Mi)=(Pi-Mi)Tvi

(1)

若di(Pi,Mi)>0则Pi点在模型的外侧，若di(Pi,Mi)<0，则Pi点在模型的内侧，见图3。

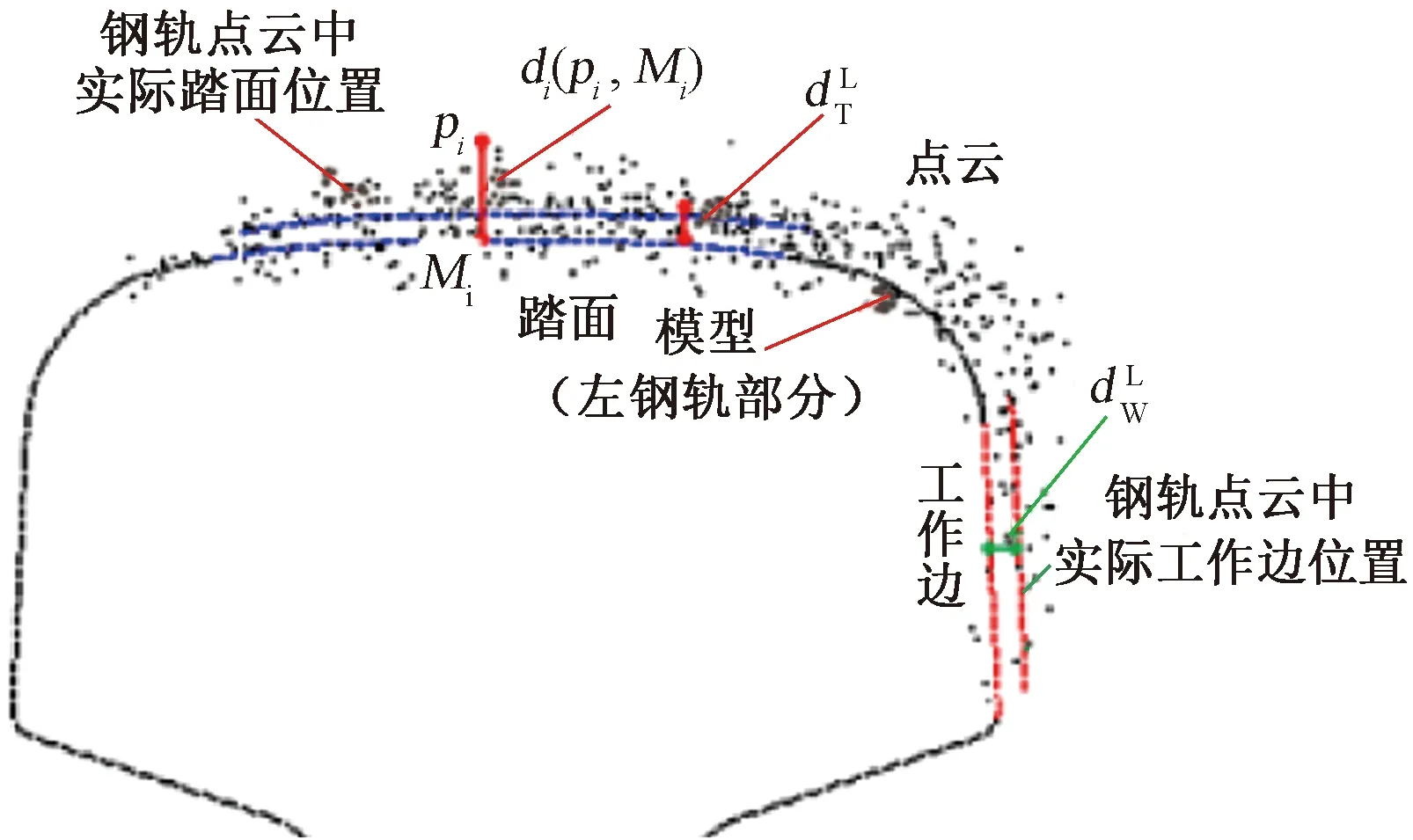
图3 左钢轨点云到模型的距离

(2)

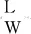
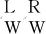
2 算法性能影响因素分析

采用模拟数据对不同实际轨距偏差、曲线段的超高和不同坡度等因素对本文提出算法性能影响进行分析。

实验中对于可变轨距轨道模型与钢轨点云的配准采用本文提出的可变轨距轨道模型配准算法；对于单钢轨轨道模型和固定轨距轨道模型与钢轨点云的配准采用ICP配准算法[13]来完成。为便于叙述，后文中两种不同的方法均称为轨道配准方法。

蒲琳忍不住给张盈盈说了两任酷帅男友的奇葩事，张盈盈思索后说：“也不能一叶障目，再交往几个说不定能遇上好的呢。”

采用模拟数据的优点在可设置不同的轨道参数，且各项参数是已知。普速铁路曲线段的内轨存在轨距加宽，轨距比直线段宽，轨距加宽数值与曲线半径、列车运行速度等相关；外轨超高最大值为150 mm。通过模拟数据对不同轨距和超高值情况进行测试。

2.1 试验数据

钢轨按照CHN60轨形状和参数进行模拟，点云长度为1 m。钢轨点云中的点间隔为1 cm，并添加均值为0 mm，服从正态分布的随机误差以模拟点云的测量误差。

2.2 轨距偏差对配准结果的影响

试验中模拟钢轨点云的轨距与标准轨距的偏差共设置了5种情况，分别为-2、0、2、4、6 mm，超高和坡度分别设为0 mm和0‰。

配准后的实验结果见图4，单钢轨轨道模型求得的左右钢轨平行性指标见图5。

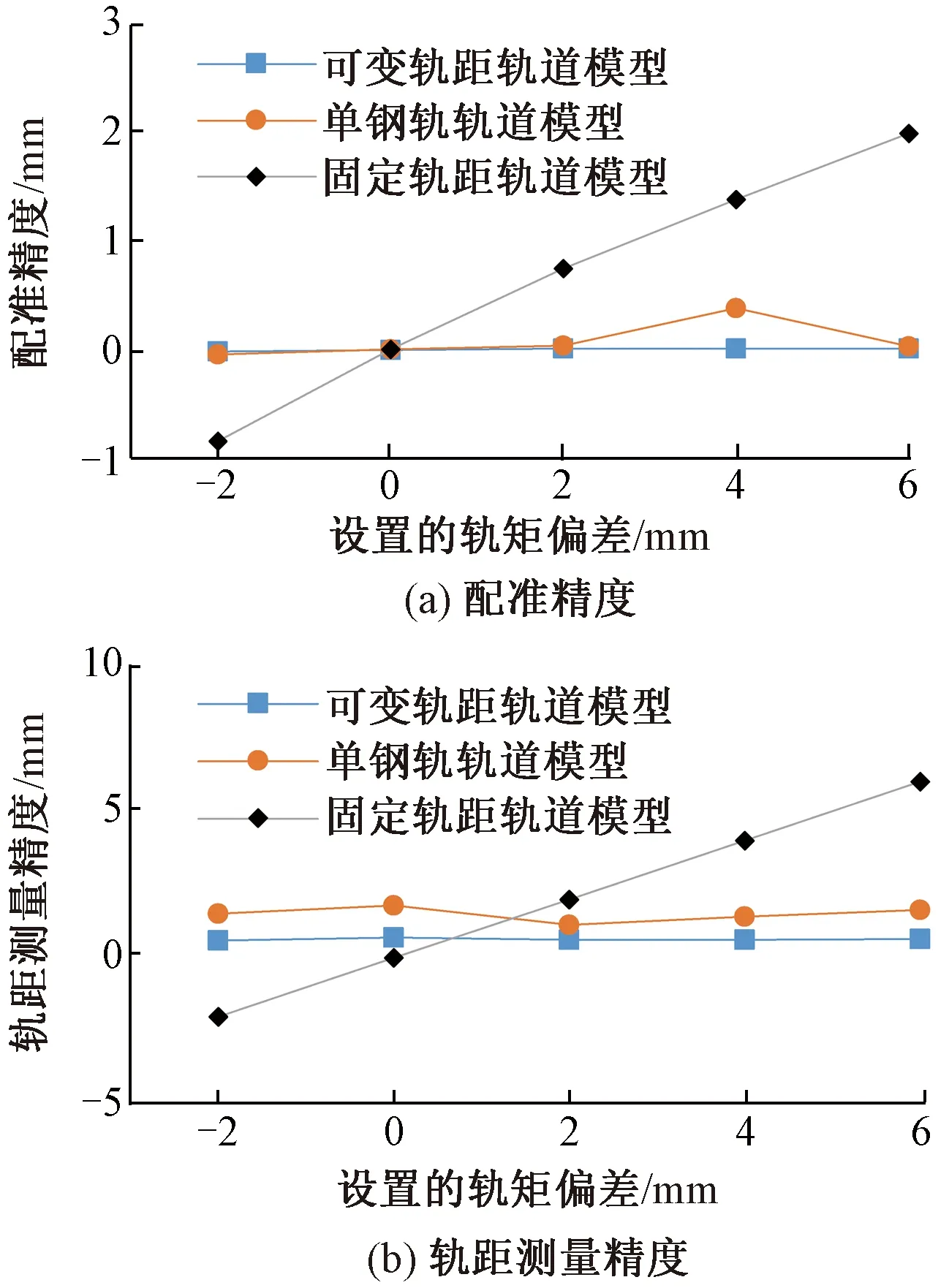
图4 轨距偏差的影响

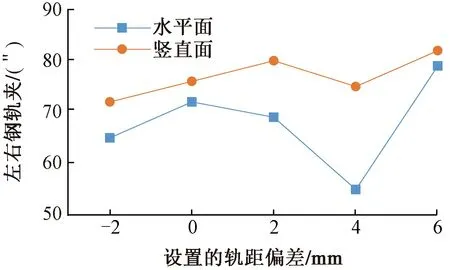
图5 单钢轨轨道模型配准给出左右钢轨平行性

由图4(a)可知，在不同轨距情况下可变轨距轨道模型和单钢轨轨道模型配准精度均较小，而对于固定轨距轨道模型配准算法，轨距偏差越大配准精度越大，这是因为配准过程中模型轨距不变导致的。显示了可变轨距模型对于不同实际钢轨轨距具有良好的适应性，均能获得较高的配准精度。

由图4(b)可知，可变轨距轨道模型配准后的轨距测量精度最高，而固定轨距轨道模型轨距测量精度最低，且差异与设定的轨距偏差基本一致。

由图5可知，单钢轨轨道模型配准后获得的左右钢轨存在一定的角度。

2.3 超高对配准结果的影响

模拟钢轨点云的超高分别设为0、30、60、90、120、150 mm，钢轨点云的轨距偏差和坡度分别设置为0 mm和0‰。配准后的实验结果见图6，单钢轨轨道模型求得的左右钢轨平行性指标见图7。

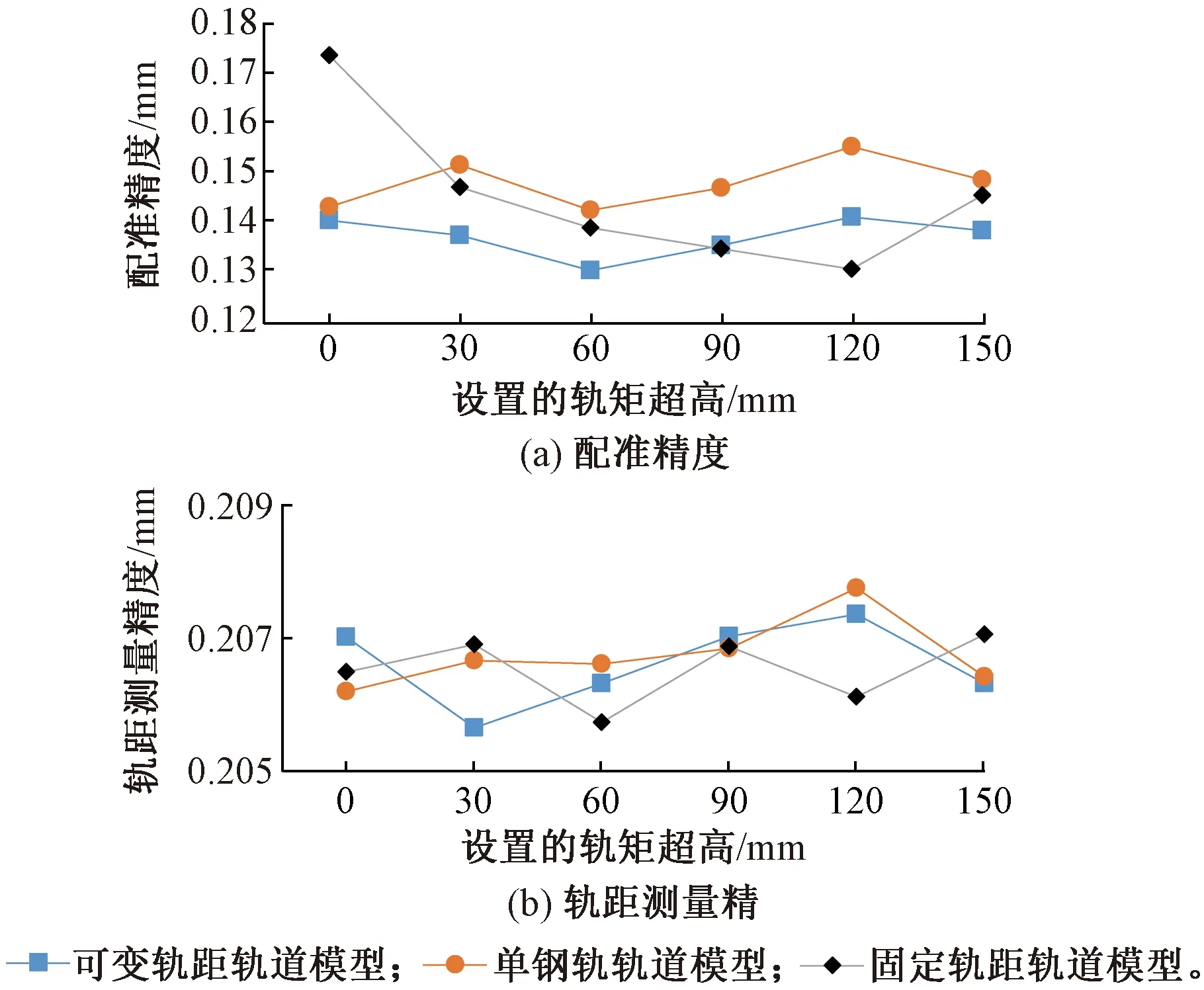
图6 轨道超高对配准精度的影响

图7 单钢轨轨道模型配准给出左右钢轨平行性

由图6(a)可知，在不同超高情况下，三种轨道模型配准精度基本相当，都非常小；由图6(b)可知，不同超高情况下的轨距测量精度也基本相当，都较小。这个结果表明轨道超高对轨道模型配准没有显著影响。

由图7可知，图7中的结果与2.2节中的结果类似，单钢轨轨道模型配准后获得的左右钢轨存在一定的角度。

3 实例应用

3.1 试验区

选取了一段长度为3 km的干线铁路作为试验区，试验区MLS点云采集速度约为40 km/h，点密度为2 200 个/m2，扫描频率为400 Hz。

选择该线路中的正线部分开展试验，其中正线区域包含直线段和曲线段，并且直线段和曲线段中均包含桥梁段数据。

首先采用基于广义高差法钢轨提取算法[4]进行钢轨点云提取，然后采用可变轨距模型配准算法来来完成模型与钢轨点云的配准，并与单钢轨轨道模型和固定轨距轨道模型配准结果进行对比。

固定轨距轨道模型中的轨距设置为1 435 mm。以人工办法确定轨距作为轨距测量值评价的基准。

3.2 实验结果及分析

为了便于结果分析和对比，选择其中路基和桥梁各500 m，均包括直线段和曲线段。各种不同类型的区段试验结果的配准精度的均值和轨距测量精度的均值见表1。

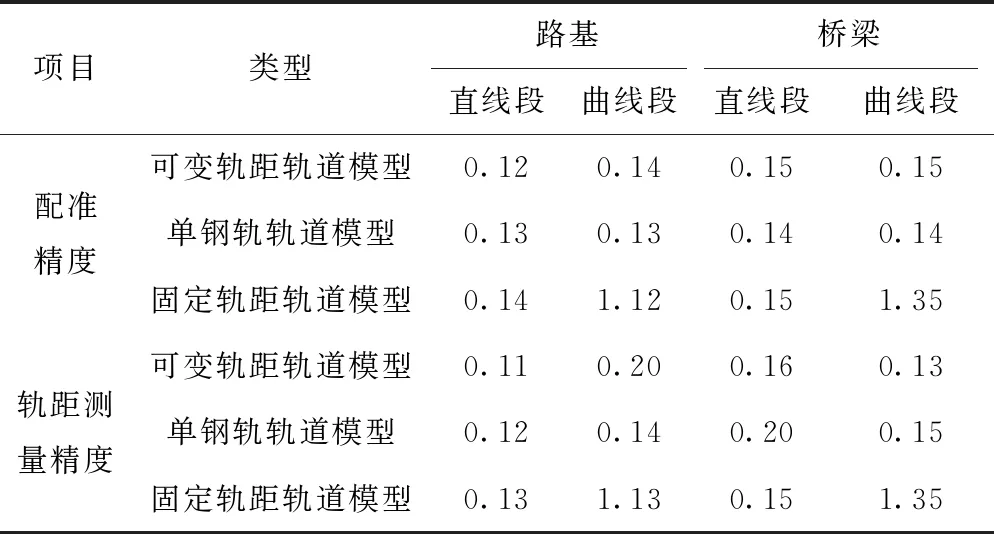
表1 不同轨道模型配准精度和轨距测量精度 mm

由表1中直线段轨道模型配准精度来看，无论是桥梁还是路基段，3种不同轨道模型的配准精度基本相当；曲线段无论是桥梁还是路基段，固定轨距轨道模型配准精度最低，低于其余两个轨道模型的配准精度。这是因为曲线段线路存在轨距加宽现象，由于实际轨道的轨距并非1 435 mm，因此产生了较大的偏差，与前面的模拟试验结论一致。

根据直线段和曲线段分别对三个轨道模型配准精度进行统计，结果见表2。

表2 配准精度 mm

由表2可知，可变轨距轨道模型与单钢轨轨距模型的配准精度基本相当；直线段各个模型的配准精度也基本相当；在存在轨距加宽的曲线段，固定轨距轨道模型的配准精度受轨距变化影响非常显著。曲线段可变轨距模型的配准精度比固定轨距模型的配准精度高88.7%。

由表1的轨距测量精度来看，固定轨距轨道模型的差异最为显著，其偏差值约等于实际线路的轨距加宽值；单钢轨模型与可变轨距轨道模型给出的轨距测量值与实际值基本一致。

对于固定轨距轨道模型和可变轨距轨道模型，配准后左右钢轨严格保持平行的，是因为配准过程中模型仅做平移。单钢轨模型配准后不同区段左右钢轨的平行性指标见表3。

表3 单钢轨轨道模型配准给出左右钢轨夹角 ″

由表3可知，左右钢轨之间无论是在水平面还是竖直面的夹角与之前模拟试验结果基本相当，存在一定的偏差。

综合以上分析，基于本文提出的可变轨距轨道模型，在配准精度、轨距测量精度、左右轨道平行性等三方面指标综合来看，显著优于基于其他两种轨道模型。

4 结论

(1)建立了可变轨距的双钢轨轨道模型，并基于该模型构建了可变轨距轨道模型与钢轨点云的配准算法。该算法在配准迭代过程种，根据点云与模型工作边的距离对轨距进行动态调整，使得配准后的钢轨模型轨距能够反映实际轨距，同时也能保证配准后左右钢轨的平行性。

(2)通过模拟试验，分析了轨距和超高对配准精度的影响，可变轨距轨道模型配准算法能够适应不同轨距的情况，并且超高的大小并不影响其性能，单钢轨模型配准难以保证左右钢轨的平行性。

(3)基于实测数据对算法性能进行了测试。在直线段部分固定轨距模型和可变轨距轨道模型的配准精度和轨距测量精度基本相当，配准精度约为0.13 mm。在曲线段，可变轨距轨道模型的配准精度和轨距测量结果显著优于固定轨距轨道模型，配准精度比固定轨距模型的配准精度高88.7%。