内部夹杂物缺陷对EA4T车轴钢裂纹萌生寿命的影响

周素霞，张 昭，吴 毅

(1.北京建筑大学 机电与车辆工程学院， 北京 100044；2.北京建筑大学 城市轨道交通车辆服役性能保障北京市重点实验室， 北京 100044；3.中国铁道科学研究院集团有限公司 金属及化学研究所， 北京 100081)

车轴钢材料在制备过程中不可避免地存在硫化物和氧化铝等内部夹杂物缺陷[1]。这些夹杂物缺陷的存在会导致附近的微观组织会出现不均匀，与钢基体的差异较大，在旋转弯曲载荷的作用下会产生较大的应力集中，导致裂纹萌生的机率升高，给列车运行安全性带来隐患。现有的对于缺陷车轴裂纹萌生机理及寿命预测的理论研究主要集中在由异物冲击造成的外部缺陷对车轴裂纹萌生的影响，所采用的理论主要包括名义应力法、局部应力应变法[2]等，这些方法忽略了材料内部夹杂物缺陷造成的微观组织不均匀性，无法研究夹杂物缺陷对裂纹萌生寿命的影响。

近些年来，研究人员采用晶体塑性有限元的方法针对不同应用领域的金属材料裂纹萌生问题进行探讨，文献[3]基于晶体塑性有限元法研究了圆形和椭圆形夹杂物对单晶铝力学性能的影响，然而研究仅限于单晶模型，没有考虑到夹杂物周围的多晶体环境。文献[4]研究了单晶镍在循环载荷下夹杂物附近的应变分布情况，并探索了夹杂物体积分数对疲劳裂纹萌生的影响。文献[5]提出了适用于铝合金材料的晶体塑性理论框架并研究了铝合金内部半圆形缺陷对其疲劳行为的影响。文献[6]基于晶体塑性有限元法研究了两个夹杂物间的相互作用对材料疲劳寿命的影响。文献[7]研究了夹杂物位置对材料疲劳失效的影响，研究结果表明，位于材料表面的夹杂物更容易诱发疲劳失效。文献[8]建立了含有各向同性球状夹杂物的晶体塑性有限元模型，模拟了拉伸载荷下夹杂物周围晶粒的晶体取向、应力分布以及塑性应变的形成规律。文献[9]使用累积塑性应变和能效密度两个指标预测了含内部缺陷的镍基合金疲劳裂纹萌生寿命。

然而，车轴材料为体心立方结构，具有48个滑移系，各个滑移系间的交互作用繁琐，滑移系的开动比较复杂，因此，需要建立适用于研究缺陷车轴裂纹萌生的体心立方晶体塑性循环本构方程。本文对EA4T车轴钢进行疲劳试验，搭建体心立方晶体塑性理论框架，构建含夹杂物缺陷的多晶集合体有限元模型，研究了多晶集合体中CaS球状夹杂物和Al2O3块状夹杂物附近应力分布规律，通过标定多晶集合体中塑性应变能密度，探索了不同夹杂物对周围材料微观组织结构的影响，最后以裂纹形成过程中能量的变化为切入点，研究了不同夹杂物对裂纹萌生寿命的影响。

1 体心立方晶体塑性理论架构

对EA4T车轴钢材料进行旋转弯曲疲劳试验，图1给出了σ=280 MPa，Nf=1×106疲劳断裂试样的断口扫描电镜形貌。裂纹源区未发现孪晶变形，滑移是EA4T车轴钢材料裂纹萌生过程中的主要变形机制。因此基于滑移理论，构建EA4T车轴钢体心晶体塑性理论框架，并通过Fortran语言编写Abaqus的UMAT用户子程序，实现理论框架有限元化。

图1 EA4T车轴钢室温下疲劳断口

在模型中，晶体变形可以分解为晶格的弹性拉伸和旋转，以及不同滑移系上的塑性滑移[10]。

F=FeFp

(1)

式中：F为总变形梯度；Fe为弹性变形梯度；Fp为滑移引起的塑性变形。

引入速度梯度张量Lp为各个滑移系的剪切速率之合，则Lp与总变形梯度F的关系为

(2)

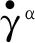
(3)

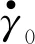
背应力演化方程为

(4)

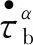
(5)

其中，Ψ0为由位错积累导致的初始硬化系数；κS为饱和强度；κ0为初始硬化强度。

2 有限元模型构建

2.1 含夹杂物缺陷的多晶集合体有限元模型构建

含夹杂物缺陷的多晶集合体有限元模型是研究模型在宏观激励下夹杂物附近材料的微观变形。为了高度还原材料夹杂物缺陷类型及材料微观结构，首先使用金相显微镜对EA4T车轴钢材料进行金相分析，见图2。

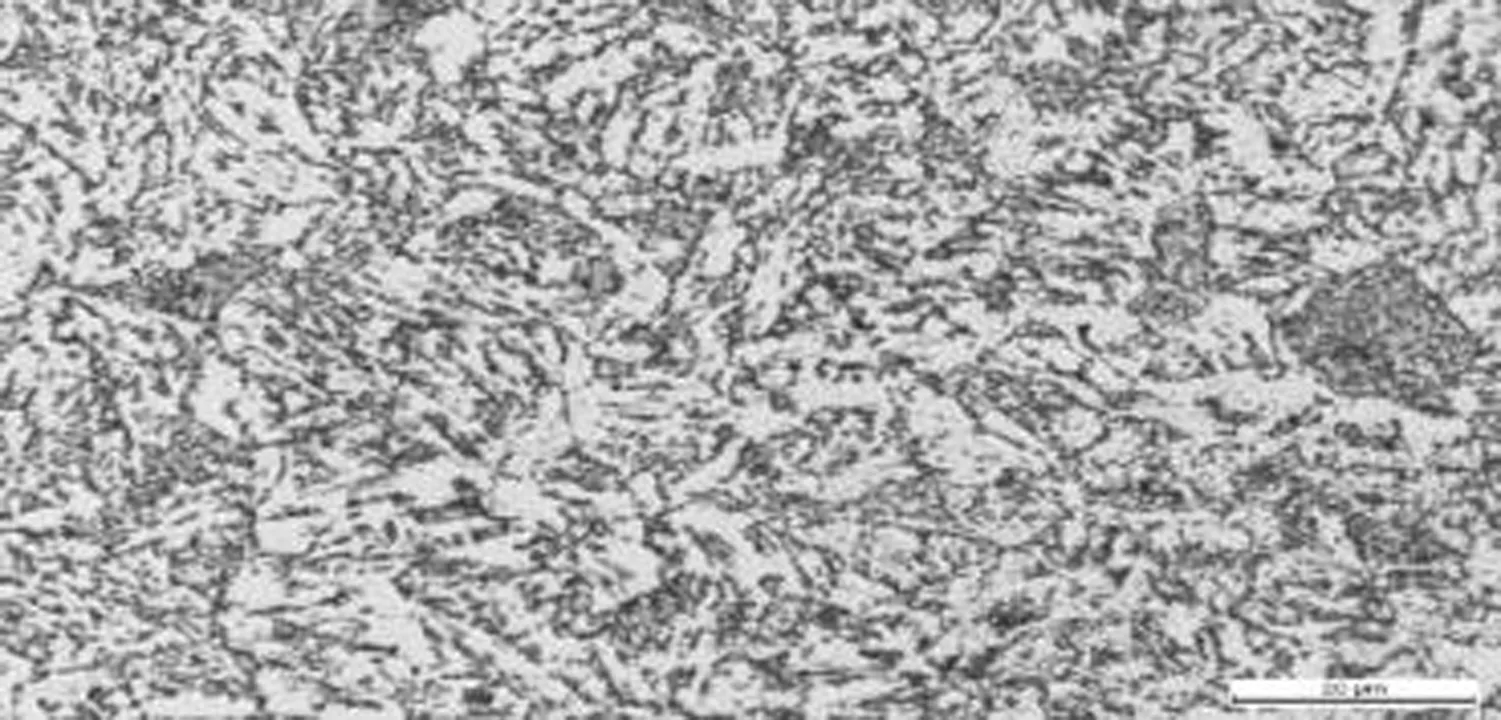
图2 EA4T车轴钢金相分析

EA4T车轴钢材料由贝氏体和回火马氏体组成，材料的晶粒度等级为6、7，材料内部夹杂物类型主要为D类球形氧化物夹杂物、B类氧化铝夹杂物以及DS类颗粒型球状氧化物详细见表1。

表1 EA4T车轴钢夹杂物评级结果

在200个晶粒的立方多晶集合体中加入CaS球状以及Al2O3块状夹杂物缺陷。依据文献[11]的研究结果，球状夹杂物及块状夹杂物缺陷的体积分数均为0.004。这种体积分数的选择旨在研究晶粒内部相对较小的夹杂物的影响。钢基体的材料参数被设定为各向异性，这样做的目的是研究夹杂物缺陷对周围不同取向晶粒的力学行为影响，晶体取向信息通过Matlab随机生成。在分析过程中，由于夹杂物缺陷与立方体被认为是分开的，因此需要设置夹杂物缺陷与立方体的接触条件，本文采用硬接触，避免在循环载荷作用下夹杂物缺陷与基体发生穿透现象。同时，用摩擦模拟接触的切向行为，对于摩擦系数u的设定，文献[12]的研究表示，摩擦系数的变化对结果的影响不大，故本文中摩擦系数u=0.1。模型信息见图3。

图3 含内部夹杂物的晶体塑性有限元模型

2.2 材料参数拟合

对于EA4T车轴钢体心立方晶体塑性理论构架中的相关参数，目前已有的研究中针对此种材料尚没有完整的参数信息。本文通过Matlab编写材料参数拟合程序结合试错法，将拟合得到的应力-应变曲线与试验曲线对比，反推出材料的微观参数。曲线对比见图4。内部夹杂物缺陷对材料裂纹萌生的影响主要体现在塑性阶段，即图4曲线中的后半段，此部分曲线拟合度高，可以用于本次研究。模型中的主要参数见表2。

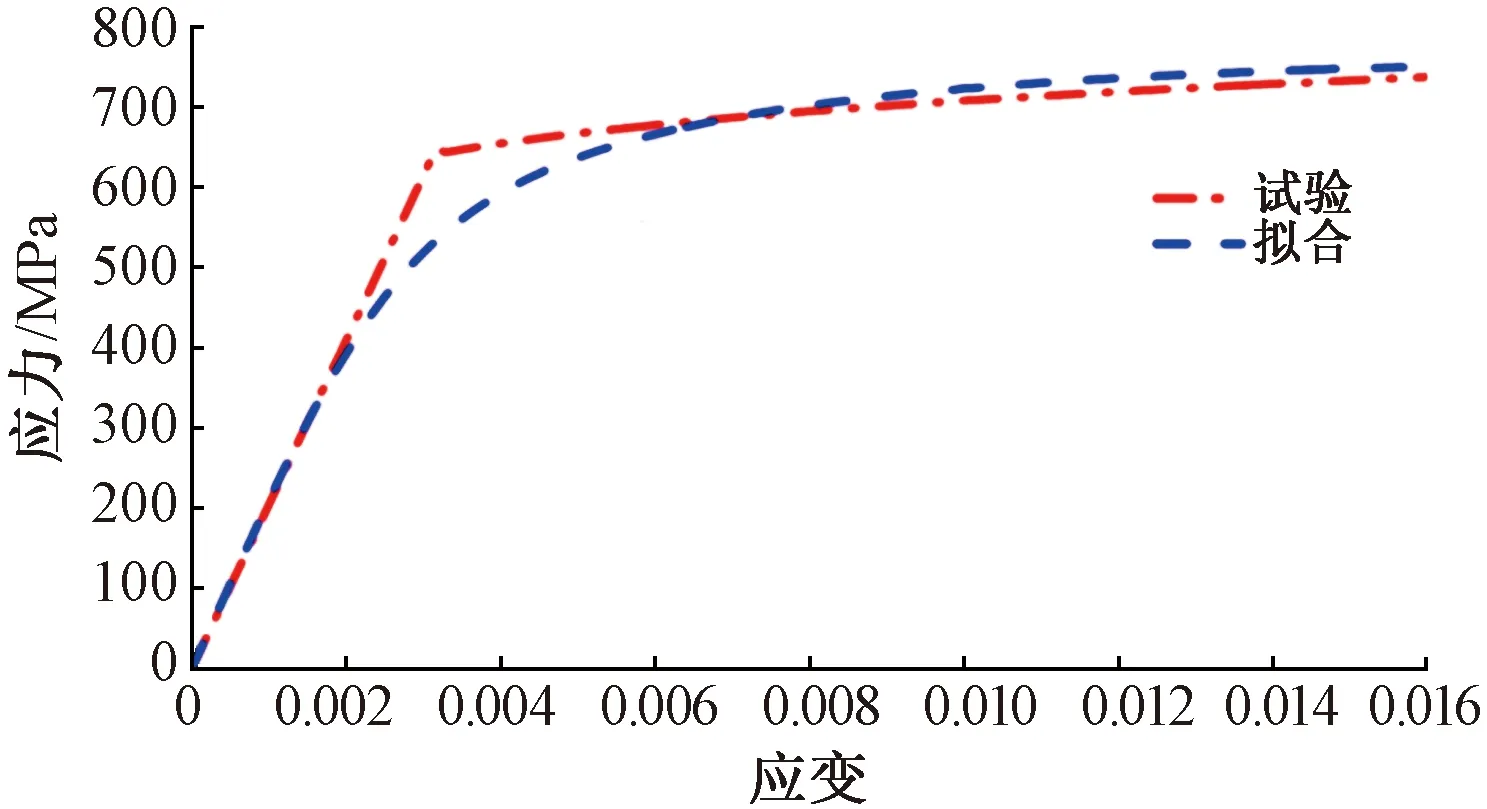
图4 材料参数拟合曲线

表2 EA4T车轴钢本构参数

2.3 边界条件

边界条件及参数随循环周期的变化见图5。

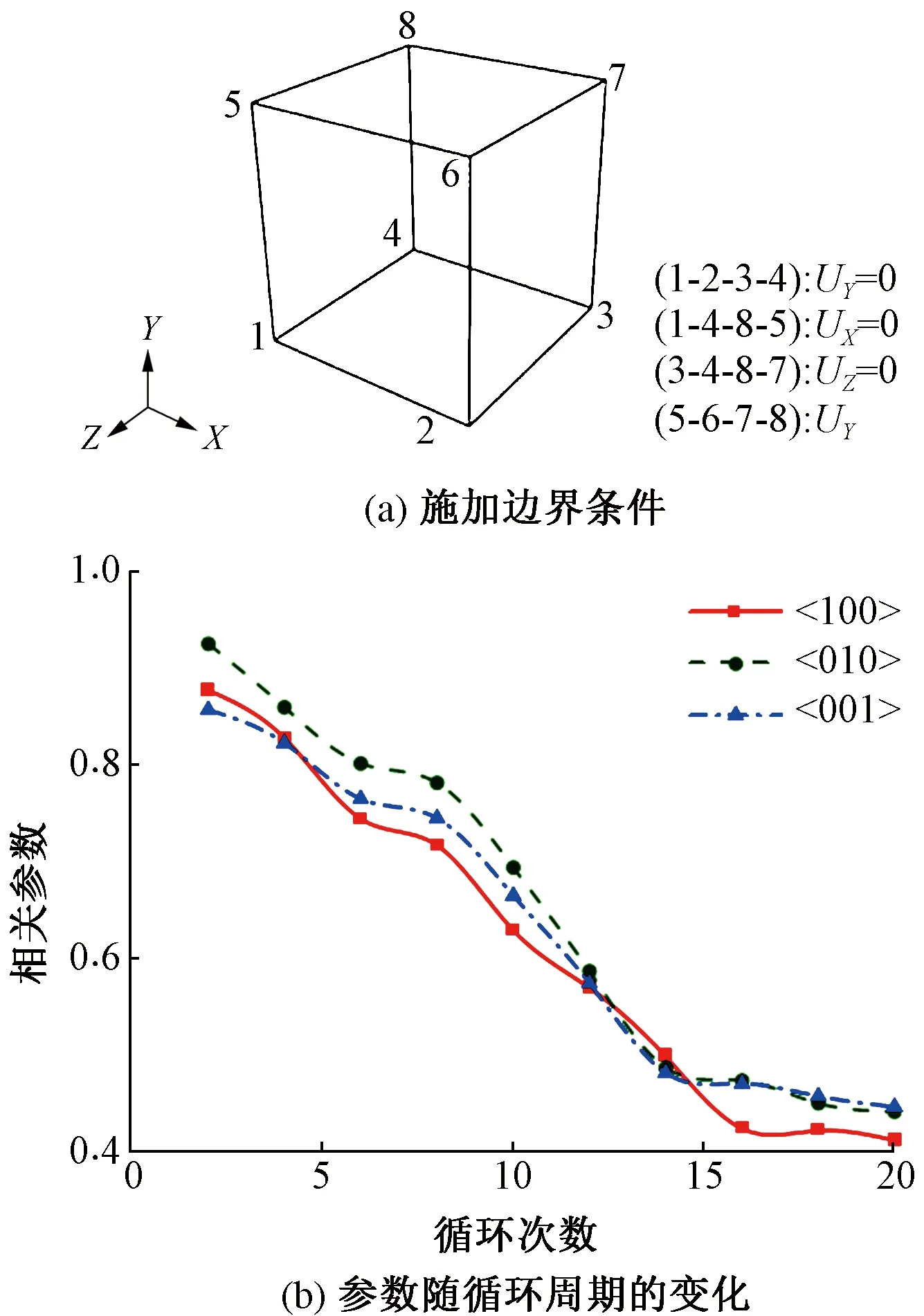
图5 边界条件及参数随循环周期的变化

在边界条件的设置上，文献[13]施加的单轴拉伸边界条件可以较好地反映出模型在宏观应力下的微观响应。然而该边界条件无法研究模型在循环载荷下的力学行为，为了研究材料内部夹杂物缺陷对疲劳裂纹萌生的影响，对边界条件进行改进，将其设置为周期性边界条件见图5(a)，约束1-2-3-4表面Y方向的位移，约束1-4-8-5表面X方向的位移，约束3-4-8-7表面Z方向的位移，在5-6-7-8上表面施加位移载荷，对该载荷绘制幅值曲线完成周期性边界条件的设置。文献[14]研究表明，随着循环周次的升高，与裂纹萌生有关的参数逐渐趋向稳定。图5(b)为模型在该边界条件下20个循环周次时与裂纹萌生有关的参数变化情况，该参数前几个周期内变化较大，随后逐步稳定，因此，考虑计算时间成本，模型中设置循环周次为20次，下文中力学分析均在此条件下进行。

3 分析与讨论

3.1 夹杂物缺陷附近应力场分布

图6描述了模型在20个循环载荷后缺陷附近最大Mises应力，可以看出，具有CaS球状夹杂物缺陷的多晶集合体Mises应力最大值集中在球体的赤道线附近，球形顶部及底部应力较低。具有Al2O3块状夹杂缺陷的多晶集合体Mises应力主要集中在缺陷的边角处，且模型中应力整体水平较高。

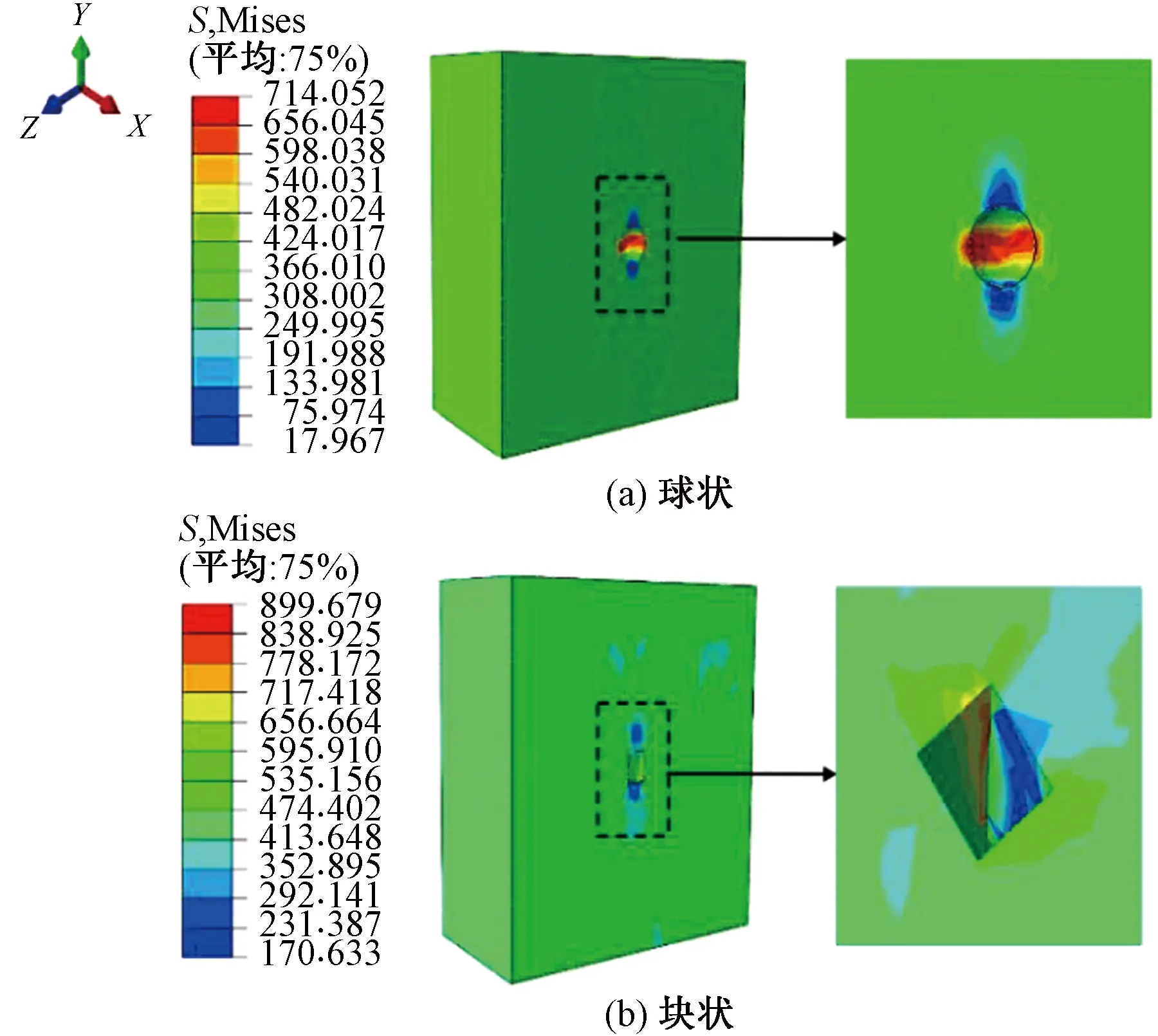
图6 含夹杂物缺陷的多晶集合体应力分布云图

图7为夹杂物在模型中的方向与位置示意图，依托图中的位置关系，分别统计模型在相同载荷下夹杂物附近<100><010><001>三个方向上自夹杂中心截面到模型边缘自由面的应力变化，如图8所示。

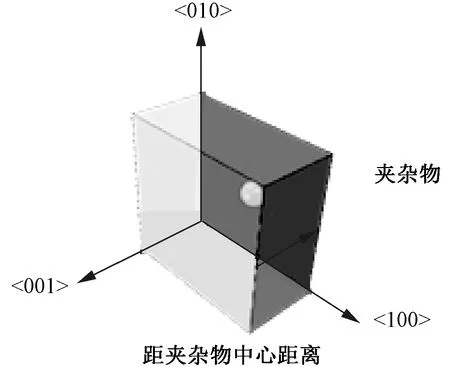
图7 夹杂物在模型中的方向与位置

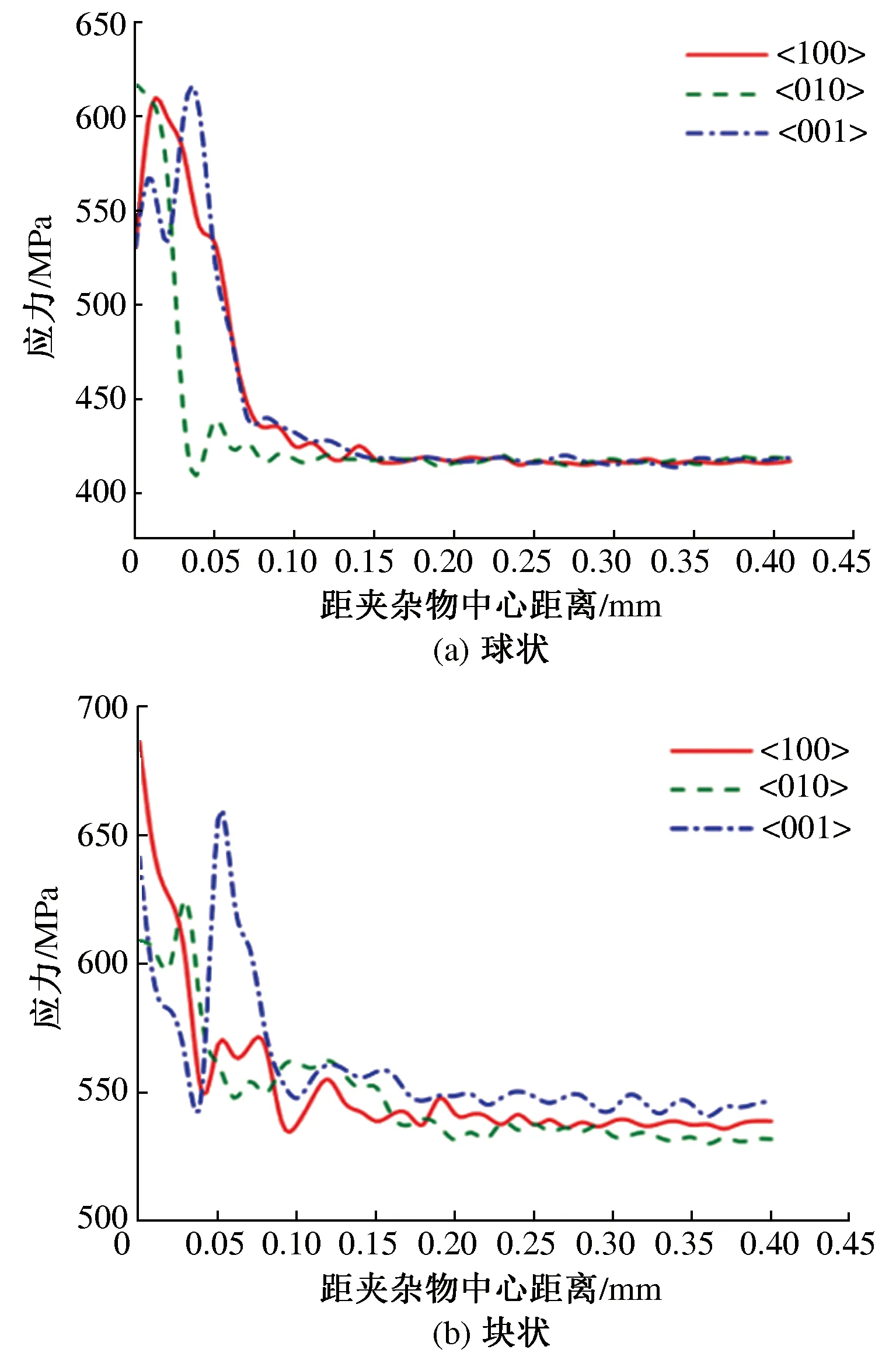
图8 夹杂物缺陷附近应力分布曲线

受夹杂物缺陷形状的影响，对于包含CaS球状夹杂物缺陷的多晶集合体，应力最大部位发生在夹杂物<001>方向上,位于球最长的圆周线附近。对于包含Al2O3块状夹杂物缺陷的多晶集合体而言，最大应力部位发生在<100>方向上，位于块状的边角附近，同时通过图中观察可以发现，对于球状缺陷模型，三个方向内的应力曲线变化趋势基本相同，而对于块状缺陷，三个方向上的应力曲线变化趋势差异较大，这主要是因为相比于圆滑球状缺陷来说，块状缺陷的边角较多，边角处更容易诱发组织不均性，产生应力集中。

受夹杂物弹性矩阵的影响，两种夹杂物缺陷模型在接近夹杂物边缘处内应力变化较大，离开夹杂中心约为0.1mm后三个方向应力趋近相同，并且应力值也大幅度降低。这是由于夹杂物的弹性矩阵与钢基体的弹性矩阵不同，材料的不连续造成应力集中。

3.2 材料内部夹杂物对裂纹萌生寿命预测参数的影响

基于能效因子的裂纹萌生寿命预测是通过计算裂纹形成过程中能量变化实现的[15]。该方法在计算过程中需要计算第N个循环载荷后的能效因子f，即

(6)

式中：E为杨氏模量；γs为表面能；σ为应力；a为裂纹尺寸；υ为泊松比；tm为最大滑移带宽；N为循环次数； Δτ为剪切应力； Δγp为剪切应变量。

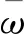
(7)

如图9所示，塑性应变能密度在夹杂物缺陷附近数值较高，随着夹杂物距离自由面距离的减小，夹杂物附近三个方向上的塑性应变能密度呈现出降低的趋势，并最终趋向平稳。对于含有球状夹杂物的多晶集合体来说，塑性应变能密度在夹杂物附近三个方向上的变化趋势基本相同，最大峰值出现在球的最大半径处，这说明球状夹杂物附近的材料微观组织结构是相似的，不存在某一方向上的材料微观结构异变。然而，相同边界条件下，对于含有块状夹杂物的多晶集合体，夹杂物附近三个方向上的塑性应变能密度变化趋势不同，且塑性应变能密度整体值较高，峰值出现在块状棱角处，块状夹杂附近三个方向上的组织结构差异较大。

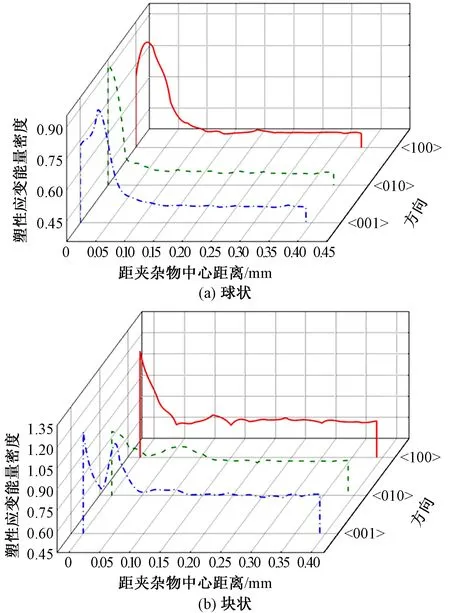
图9 含夹杂物缺陷的多晶集合体塑性应变能量密度分布情况

由此可见，不同形状的夹杂物会对材料微观组织结构造成不同程度的破坏，表面光滑的夹杂物周围微观组织结构趋近相同，带有棱角的夹杂物周围微观组织结构差异较大，相同边界条件下，块状夹杂缺陷的塑性应变能量密度高于球状夹杂缺陷，更容易诱发材料发生塑性变形。

3.3 不同夹杂物对裂纹萌生寿命的影响

裂纹萌生需要能量，文献[16]提出通过吉布斯自由能变化值来预测裂纹萌生，假定模型在循环加载过程中，施加载荷的一小部分能量储存在模型中，当累积的能量大于形成新表面的能量时，将导致裂纹萌生。裂纹预测机理和过程为

ΔG=-W(e)-ANδ+2Aγs

(8)

式中：ΔG为吉布斯自由能变化值；A为裂纹的面积；N为循环次数；δ为每个循环后裂纹的储能增加量；γs为表面能；W(e)为储存的弹性能。

W(e)、δ计算式分别为

(9)

(10)

式中：δ为柯西应力。

假设裂纹的面积A为半圆形，裂纹长度a随着循环次数的增加而增加，并且当dΔG/da=0时达到临界值。则

(11)

N为裂纹萌生寿命，所以

(12)

将上文中定义的塑性应变能密度带入式(12)，即可得

(13)

结合疲劳试验与有限元仿真结果，寿命计算算法中主要的参数见表3。

表3 寿命预测算法中的相关参数

根据模型中夹杂物附近的塑性应变能量变化以及有限元仿真结果，计算出含球状夹杂物缺陷与块状夹杂物缺陷的多晶集合体中裂纹萌生寿命分布，见图10。寿命曲线呈现波动变化，这是由于多晶集合体为各向异性，晶界两侧的晶粒存在取向差异，应变在晶粒内部产生局域化而应力在晶界内局域化，这就导致式(10)的结果产生波动变化，从而寿命预测曲线是波动曲线并非光滑。

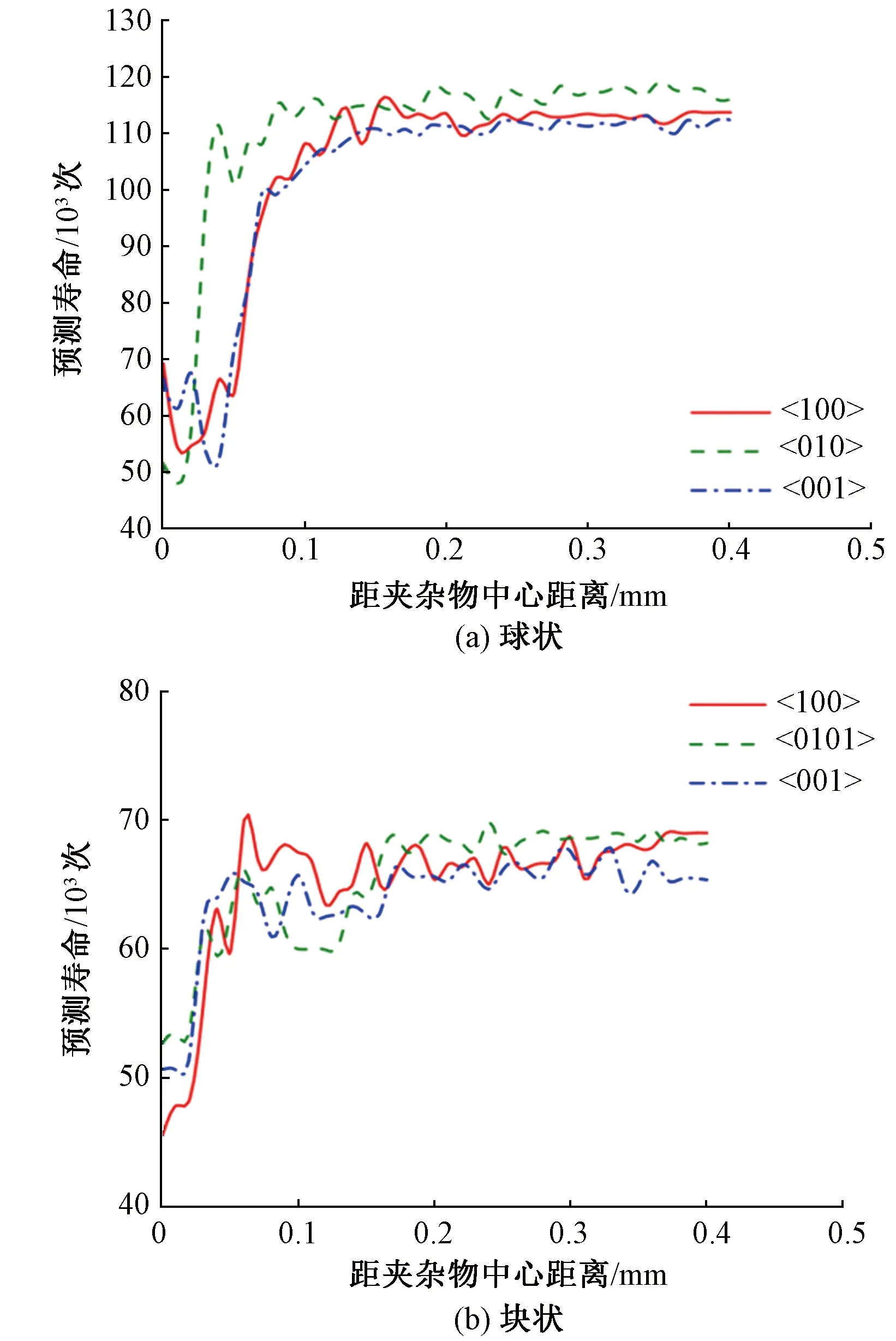
图10 含夹杂物模型的裂纹萌生寿命

夹杂物材料及形态对裂纹萌生影响较大，球状夹杂物缺陷裂纹萌生寿命在距离夹杂物中心约0～0.05mm范围内先降低至最低点随后逐渐升高，寿命最低点位于<010>方向上，球的最大半径附近，说明对于材料中的球状缺陷，裂纹容易萌生于球的最大圆周处；块状夹杂物缺陷裂纹萌生寿命在距离夹杂物中心约0～0.05mm范围内先升高，接着出现小幅度下降后继续升高。含有块状夹杂物的多晶集合体相比于含有球状夹杂物的多晶集合体裂纹萌生寿命更低。这与文献[17]中的结果一致，块状夹杂更容易诱发疲劳裂纹萌生。

4 结论

本文构建了体心立方晶体塑性理论框架，利用晶体塑性有限元模拟方法研究了车轴钢材料内部CaS球状夹杂物缺陷和Al2O3块状夹杂物缺陷对EA4T车轴钢基体应力场的影响，通过不同缺陷模型中应变能量密度分布情况，讨论了不同缺陷对材料裂纹萌生寿命的影响。主要研究成果可以总结为以下几点：

(1)通过EA4T车轴钢疲劳试样断口分析可以观察到晶体滑移是EA4T车轴钢材料疲劳裂纹源区的主要变形机制。

(2)材料内部夹杂物缺陷形状以及弹性矩阵的差异是引起应力集中的主要诱因，相同加载条件下，Al2O3块状夹杂物缺陷通常比CaS球状缺陷的应力集中现象更为明显。

(3)Al2O3块状夹杂物周围塑性应变能量密度较高，同时，三个方向上的塑性应变能量密度差异较大，容易诱发材料发生塑性变形。

(4)对于材料中的球状夹杂物缺陷，裂纹容易萌生于球形表面处；块状夹杂物裂纹萌生最先发生在<100>方向上，距离夹杂物中心距离约0.05mm处。相同条件下，Al2O3块状夹杂物缺陷更容易诱发疲劳裂纹萌生。