基于三维编织模型的棉纤维集合体压缩过程有限元建模与仿真
吴 帆, 李 勇, 陈晓川, 汪 军, 徐敏俊
1. 东华大学 机械工程学院, 上海 201620; 2. 塔里木大学 机械电气化工程学院, 新疆 阿拉尔 843300;3. 东华大学 纺织学院, 上海 201620)
棉花是重要的经济作物与纺织原料,作为典型的絮状纤维集合体,棉花是由大量棉纤维缠绕堆积而成的。采摘与加工后的棉花都需要经过多次压缩与放松过程。在压缩过程中,由于内部棉纤维长时间处于高应力状态,棉纤维的性能会受到影响,其自身的某些性质也会发生改变。倘若压应力过大,棉纤维可能会在相互接触处形成压痕,甚至于开裂,这将使得棉纤维的力学强度发生改变,从而影响棉花的品质[1]。
棉纤维集合体的压缩行为包含大量纤维的弯曲、滑移、摩擦以及局部拉伸等,内部纤维的运动行为几乎没有任何规律性,十分复杂。许多学者都对棉纤维集合体在加压释压过程中的力学行为进行研究。其中较为著名的是Van Wyk忽略了纤维扭转、滑移及拉伸,提出的纤维集合体压力-体积关系式[2]。Jing等[3]指出,虽然学者都基于不同的假设提出了许多纤维集合体压缩的经典理论,但纤维集合体压缩过程的细节仍然不甚明了,并对多种纤维集合体进行了压缩试验来分析其在压缩-回复过程中的力学行为。李勇等[4-5]将棉纤维集合体视为多孔材料,研究了棉纤维集合体的压缩性能,并建立棉纤维集合体应力与相对密度的关系。
随着计算机技术的发展,计算机仿真技术逐渐成熟,为研究纤维及其集合体提供了一个新的思路。Perumalsamy等[6]基于单面针织物的细观结构,建立了单面针织物的有限元模型,并进行非线性有限元分析,成功预测了单面针织物在拉伸作用下的变形行为。Chen等[7]在复合材料的建模思想上,提出了层合板的棉朵模型,其将棉纤维集合体的内部纤维在二维平面上以一定角度平铺排列,再将多个二维平面层堆叠组合为一个整体,形成棉纤维集合体模型;在此模型的基础上,利用有限元分析方法模拟棉花的轧花过程,分析了不同轧花条件对棉花性能的影响。Xu等[8]在泡沫材料压缩曲线与棉纤维集合体压缩曲线具有相似性的基础上,结合Kelvin十四面体模型,构建了棉纤维集合体压缩过程的宏观模型,成功模拟了棉纤维集合体压缩过程的宏观力学性能。孔凡婷等[9]利用离散元技术,将籽棉视为球体颗粒,通过定义合适的接触模型,预测籽棉在压实搅龙作用下,籽棉总压缩力随压缩时间的变化情况。但是,以上模型都集中于分析纤维集合体的宏观力学性能,难以探究纤维集合体内部纤维的受力情况。为研究棉纤维集合体压缩性能,本文利用有限元技术对棉纤维集合体压缩过程中内部纤维的相互作用做出分析,基于三维编织建模思想构建了新的棉纤维集合体模型。
1 棉纤维集合体三维编织模型构建
棉纤维集合体的内部纤维空间关系是复杂无序的。想要建立完全反映纤维实际的几何形状、分布状况等特征的模型是十分困难的。在对棉纤维形状以及分布状况进行一些合理的近似基础上,三维编织理论是通过纤维分布方向、纤维体积分数、纤维弯曲形状等编织工艺参数,研究纤维的空间几何构造,详细论述对空间多向分布的纤维束建立几何模型的方法。
棉纤维集合体内部的纤维分布与取向是没有规律性的,为充分考虑到棉纤维的方向性,将内部纤维方向简化为空间上的4个方向。假设纤维束的截面为圆形,建立如图1(a)所示的内部单元,并通过如图1(b)、(c)所示的三胞模型的表面单元与角单元来反映棉纤维的弯曲特征,棉纤维的体积分数则通过赋予合适的纤维束直径来确定。为便于仿真计算,取三胞模型中的18个内部单元进行周期排布,并添加表面单元与角单元,将各模型单元连接为缠绕在一起的一个整体。建立的棉纤维集合体几何结构实体模型如图2所示。需要说明的是,由于结构限制,纤维间相互作用以接触为主,忽略了纤维间的摩擦。

图1 棉纤维集合体单胞几何结构模型

图2 棉纤维集合体实体模型
棉纤维集合体的相对密度是与性能直接相关的参数。在数值上,纤维的体积分数与编织体纤维的相对密度是相等的。纤维的体积分数定义为纤维的体积与整个编织体的体积之比:
式中:Vf为棉纤维集合体的纤维体积分数;Vf1、Vf2、Vf3分别为内部单元、表面单元和角单元个数;Vg1、Vg2、Vg3分别为内部单元、表面单元和角单元纤维体积,mm3;V为棉纤维集合体的体积,mm3。
2 棉纤维集合体压缩过程仿真
2.1 参数设置
参数设置主要包括:材料参数的定义、模型建立与网格划分、载荷与约束条件的设置以及分析类型设置4个部分。
材料参数的定义:压板的泊松比为0.29,密度为7 850 kg/m3,弹性模量为2.07×105MPa;棉纤维[7]的泊松比为0.4,密度为1 530 kg/m3。设置棉纤维集合体压缩模量随着其相对密度的变化而变化,根据压缩试验的测量计算,棉花初始相对密度为0.041,回潮率为8.8%,质量为160 g,品种为新陆中37号。棉纤维集合体的压缩模量与相对密度的关系[8]如表1所示。
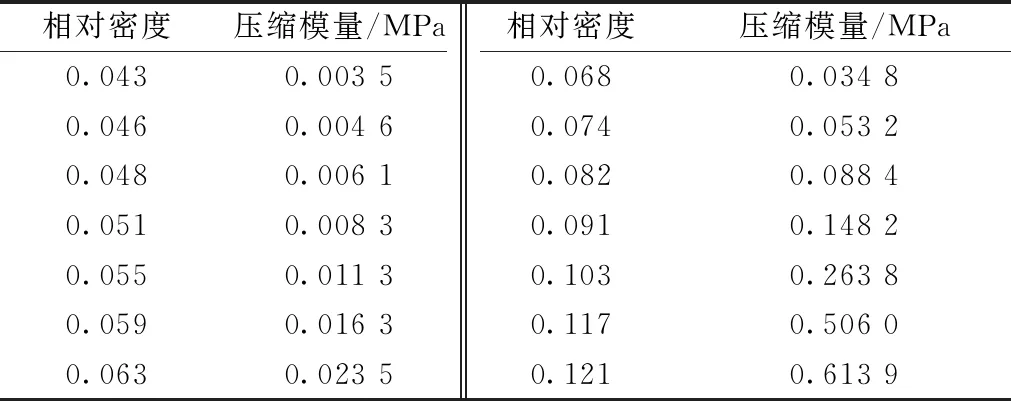
表1 回潮率为8.8%时棉纤维集合体的压缩模量
模型建立与网格划分:在棉纤维集合体模型上下两端建立压板模型,对于压板与棉纤维集合体模型,在有限元软件ANSYS中都可采用Solid185三维实体单元进行网格划分,划分后的有限元模型如图3所示。
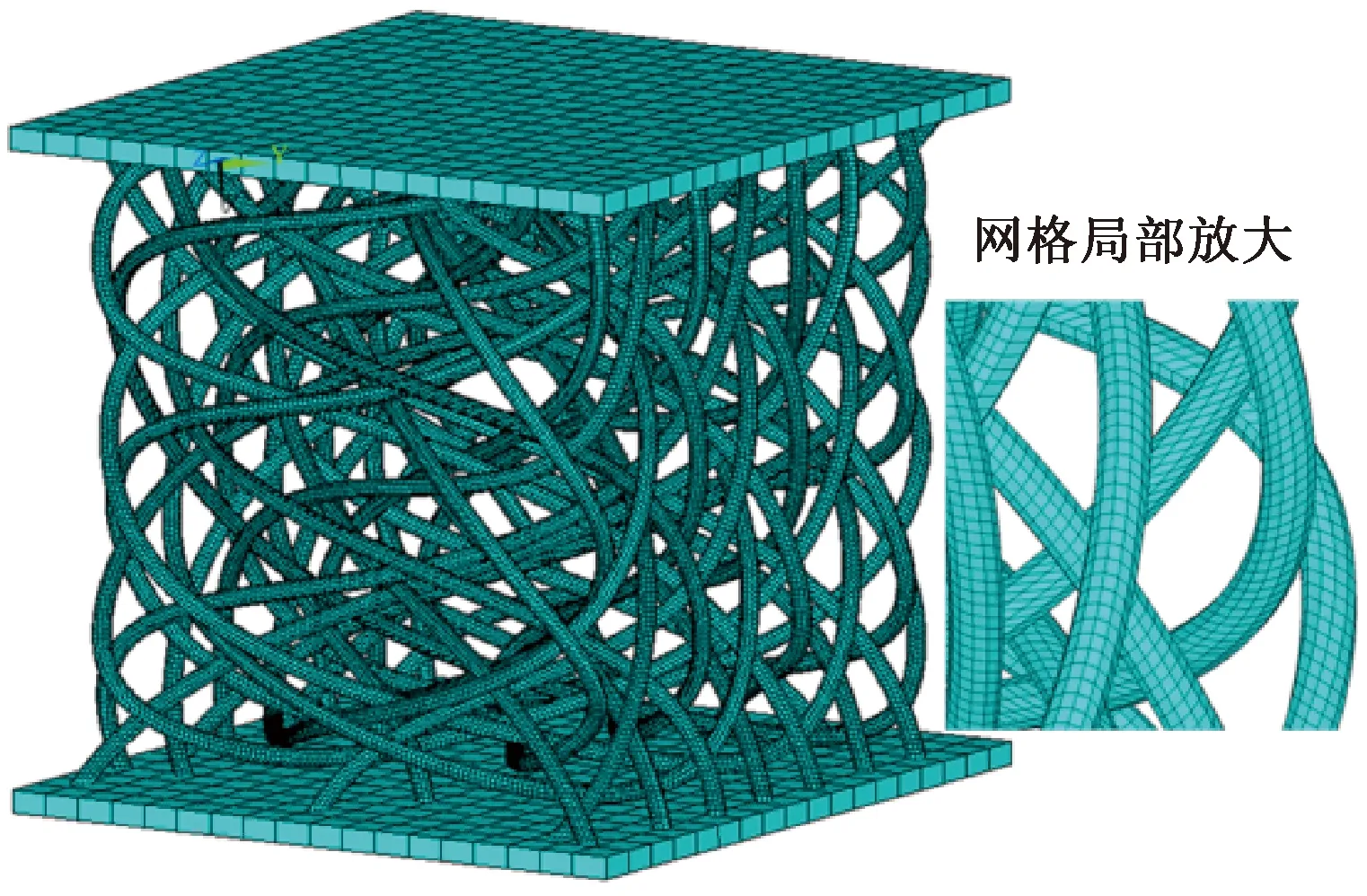
图3 棉纤维集合体有限元模型
载荷与约束条件的设置:棉纤维集合体的压缩行为是侧限单轴压缩,因此,参考压缩试验的约束条件,约束上压板的水平自由度,约束下压板所有自由度,约束棉纤维集合体水平方向的自由度;同时设置纤维束之间的接触。在上压板施加65%压缩率的轴向位移,压缩位移约为9.1 mm,设置压板加载速度为100 mm/min。
分析类型设置:分析类型为静态,选择稀疏矩阵直接法求解器(SPARSE)进行求解。
2.2 有限元分析结果与试验数据比较
图4示出回潮率为8.8%的棉纤维集合体压缩过程应力云图。

图4 回潮率为8.8%时棉纤维集合体压缩过程应力云图
图5与表2示出棉纤维集合体的压应力随压缩率以及相对密度变化关系的仿真结果以及试验结果。在表2中,相对误差作为评估压缩试验值与有限元分析(FEA)值之间误差大小的参考值,定义为绝对误差与约定真值之比。设试验值为约定真值,则相对误差可表示为:
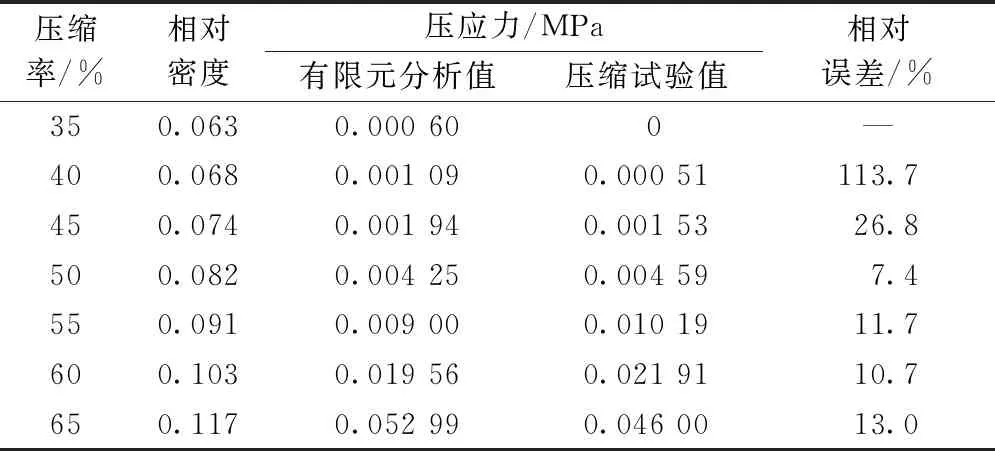
表2 棉纤维集合体压应力有限元分析值与试验值对比

图5 压应力与压缩率及相对密度关系曲线
式中:x为有限元分析值,MPa;X为压缩试验值,MPa。
由图4可见,在压缩作用下,棉纤维集合体内部纤维发生了大变形,纤维应力也随着压缩的进行而增加。由图4(a)、(b)可见,压缩前期内部纤维应力分部较为均匀,纤维以自身的弯曲变形及滑移为主要变形形式,应力云图整体呈浅蓝色。当压缩率由30%增加至45%时,内部纤维应力由0.002~0.004 MPa提高至0.008~0.017 MPa。由图4(c)、(d)可见,压缩后期纤维应力分布不均匀,大致可分为中间深蓝色的滑移区及两侧浅蓝色的弯曲变形区2个部分。中间深蓝色滑移区的棉纤维以轴向滑移变形为主,应力较小;而两侧浅蓝色弯曲变形区的棉纤维则以弯曲变形为主,应力较大。当压缩率为60%时,滑移区应力基本小于0.05 MPa,弯曲变形区应力基本大于0.09 MPa;当压缩率增加至65%时,滑移区应力小于0.09 MPa,弯曲变形区应力基本大于0.17 MPa。弯曲变形区的纤维应力明显大于滑移区纤维应力,因此,在压缩过程中棉纤维在弯曲变形的局部区域的受力更加严峻,棉纤维也更易损伤。
从图5与表2可以看出:随着压缩过程的进行,棉纤维集合体整体的压应力不断增大;相对误差存在波动,但总的来说随着压缩率与相对密度的增加,相对误差不断减小。造成误差波动的因素主要为模型和试验条件。对于模型来说,在压缩过程的前期模型结构更为松散,更容易被压缩,因此,压应力会相对较小。由于压缩前期的压应力非常小,而试验所使用的传感器所能测量的最小应力为0.000 51 MPa,因此,当棉纤维集合体应力小于0.000 51 MPa时,传感器难以测出;且即使棉纤维集合体应力达到0.000 51 MPa,其应力增量也很小,传感器由于灵敏度的限制,难以测量出相应压缩率下的理想应力值。此外,由于棉纤维集合体应力增量小,试验中更易受到外界干扰,造成更大误差。综合模型及试验这2个因素,造成了压缩前期的相对误差总体大于压缩后期的现象。
在实际压缩工艺中,棉纤维集合体都需要被压缩至较高的相对密度,尽量减小体积以方便储存、运输。根据棉花包装的GB 6975—2013《棉花包装》,棉花打包后的棉纤维集合体的整体密度在315 kg/m3以上,即棉纤维集合体的相对密度达到了0.2以上,因此,对于实际压缩工艺,棉纤维集合体在相对密度较高情况下的受力情况更值得关注。当棉纤维集合体压缩至相对密度大于0.1后,有限元分析值与压缩试验值的相对误差为10.7%和13.0%,相对误差较小,说明该模型相对合理。
3 回潮率对压缩过程的影响分析
棉纤维的吸湿是一个比较复杂的物理化学现象,一般而言,棉纤维的弹性随着回潮率升高而降低,棉纤维集合体的压缩性能也将发生一定变化。取回潮率分别为4.2%、6.6%、8.8%、10.7%、12.3%、14.1%的棉纤维集合体,从压缩模量角度分析回潮率变化对棉纤维集合体压缩性能的影响。根据压缩试验的测量计算,当初始相对密度为0.041,不同回潮率下棉纤维集合体的压缩模量与相对密度关系如图6所示[8]。可以看到,棉纤维集合体的压缩模量整体上随着回潮率升高,呈现先降低再升高的趋势。这主要是因为纤维中大分子链间的作用力随着回潮率增大而减弱,导致棉纤维弹性下降,纤维间的相互作用力也随之变小,压缩模量也因此下降;但当回潮率上升到一定程度后,棉纤维弹性的过度下降导致其局部孔隙结构在外力作用下迅速破坏,留给纤维移动和重排的空间减少,局部棉纤维排列变得紧密,纤维过早的开始相互挤压导致压缩模量上升。由于该过程相对复杂,因此,在有限元分析中,通过图6所示的压缩模量在不同回潮率下的变化来表现该压缩特性。重复上述有限元分析环节,得到不同回潮率下棉纤维集合体65%压缩率时的应力云图(如图7所示)。

图6 不同回潮率下棉纤维集合体压缩模量与相对密度关系曲线
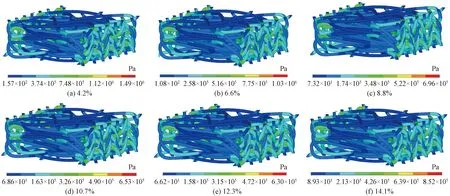
图7 不同回潮率棉纤维集合体压缩65%时应力云图
由图7可以看到,不同回潮率的棉纤维集合体在压缩至65%时,其局部纤维的应力分布基本一致,可以大致分为中间深蓝色滑移区及两侧浅蓝色弯曲变形区,发生弯曲变形的棉纤维应力大于滑移的棉纤维。表3示出有限元分析得到的棉纤维集合体内部纤维的应力。可以看到,不同回潮率的棉纤维集合体压缩至65%时,发生弯曲变形的棉纤维应力几乎比发生滑移的棉纤维应力大了1倍。说明棉纤维集合体的回潮率对压应力有很大的影响,回潮率过高或过低都会使得应力增大,因此,控制回潮率可减小棉纤维集合体的应力。总的来说,回潮率为4.2%时纤维的受力最大,回潮率在8.8%~12.3%范围时,纤维的应力值相对较小。

表3 有限元分析所得不同回潮率棉纤维集合体内部纤维应力
在实际生产加工中,尽可能地降低棉纤维集合体的应力值是有利的,因为这一方面可使得棉包的稳定性更好,另一方面也减小了内部纤维损伤的可能性。但是,回潮率对棉花加工性能的影响比较复杂,比如在轧花工艺中会影响短绒率,在纺纱工艺中会影响成纱强度等[10]。根据前面的分析,当回潮率为8.8%、10.7%及12.3%时,应力值是相对较小的。但当棉纤维集合体回潮率达到10%以上时,在棉包储存过程中棉花品质会发生较大变化[11], 可能会对棉纤维在其他加工工艺中的性能产生影响,因此,对于压缩打包而言,控制回潮率为8.8%左右是较为适宜的。根据GB/T 9994—2018《纺织材料公定回潮率》,棉纤维的公定回潮率是8.5%,二者十分相近,说明本文分析结果符合已有经验。
4 结 论
1)基于三维编织复合材料的细观几何建模思想,提出了一种棉纤维集合体模型。利用该模型成功模拟了棉纤维集合体在压缩过程中压应力的变化情况,分析结果符合试验数据,验证了模型的合理性。
2)分析了在压缩过程中,回潮率对棉纤维集合体压应力以及内部纤维应力状况的影响。结果表明,压缩过程中控制回潮率为8.8%左右是较为适宜的,此时棉纤维集合体的压应力以及内部纤维应力较小,纤维接触处的应力也相对较小,棉纤维不易产生开裂及压痕,有利于压缩过程的进行,也有利于提高棉包的稳定性。研究结果对实际生产过程中棉纤维集合体压缩打包工艺及参数的选取有一定参考价值。

