面向柔性面料立体缝纫的随形机械手设计

高晓飞， 齐立哲， 孙云权

复旦大学 工程与应用技术研究院， 上海 200433)

服装是人们生活中不可或缺的物品之一，其质量的好坏过多依赖于人工技能水平的高低，具有一定的不稳定性，尤其是缝纫工艺环节，对最终的服装质量有着决定性影响，而立体缝纫又是缝纫工艺中最难实现自动化的一种。目前，人工进行立体缝纫的衣服一致性并不是很好，受各种人为因素的影响，可能会出现波浪、不对称、起皱、跳针跳线、骨位错开、不圆顺等缺陷，严重影响衣服的外观和质量。综上，传统的缝纫方式不能满足立体缝纫一致性的要求，需要寻找一种新的缝纫方式来代替人工完成立体缝纫，以此来保证缝纫质量的稳定性。目前，利用机器人技术、信息技术和自动化控制工程等学科的最新研究理论与技术，研究自动化缝纫和柔性面料加工技术成为服装加工行业的热点。

目前，行业内对自动化立体缝纫的研究分为以下几个方面。1)基于视觉的自动化立体缝纫：Kim等[1]开发了自动缝纫机控制器和三维测量系统，可以确定立体缝纫的最佳工艺参数；Yoshimi等[2]针对三维立体缝纫织物开发了一套机器人系统，在低速喂料的前提下，可进行三维曲面缝制；Shungo[3]针对服装缝制过程的自动化问题，设计了一套双臂缝纫系统，实现了立体缝纫过程中的自动送料。2)基于力位混合信息的立体缝纫技术：如美国Softwear公司[4]研发了一条适用于T恤生产的全自动生产线，通过视觉引导缝纫，极大地提高了自动化生产效率；Schrimpf等[5-6]提出了双臂协同作业进行缝纫的方案，主要由2款优傲机器人协作运动，在激光视觉的引导下进行缝纫操作[7]，此外作者还通过三角测量的原理设计了一套视觉系统，用于缝纫过程中的边缘检测系统[8-9]，能够让机械臂在缝纫过程中完成实时的误差调节，以达到缝纫效果最优的目的，为控制面料缝纫过程的稳定性，作者还加入了力控因素[10]，保证缝纫质量的稳定性。3)硬质材料立体缝纫技术：德国KSL公司[11]研制的自动化缝纫系统由机器人携带缝纫机头对材料进行缝纫，目前已经能够针对皮革、凉席等硬质材料进行自动化缝纫，但无法应用于柔软性面料；Jonathan Zornow研发出一种热塑性溶剂，可将面料硬化增强其刚度，便于机器人抓取操作，加工完成后将面料溶于水，又会恢复面料原本的特性，这样更容易实现服装自动化加工，但其成本和可操作性都有待优化；此外，还有一些学者对缝纫过程中的智能控制进行研究[12-14]，主要是为缝纫过程自动化控制提供一些理论模型。

虽然行业内的专家经过多年研究取得了一定研究成果，但在实际应用中还存在一定问题。1)柔软面料精确定位抓取的难题。由于不同尺码的衣服尺寸具有差异性，在自动化缝纫过程中如果衣服换码加工，就得对生产线进行较大的改动，所以如何解决不同尺码面料的自适应抓取问题成为关键，而且还需要自动适应不同形状的边缘形状。2)面料缝制过程中自动纠偏的难题。在缝纫过程中，基于机器振动因素和面料本身的柔软特性，面料会发生偏移，缝纫轨迹会发生偏差，传统的模板法和机器人离线编程法都无法进行在线纠偏，那么如何解决缝纫过程中面料出现偏差时自动纠偏的难题成为难点。针对上述问题，本文通过对缝纫工艺进行分析，设计了一款适用于立体缝纫的随形机械手装置，以解决自适应撑布问题和缝纫过程中自动调布的问题。

1 随形机械手机构设计及自由度分析

1.1 工艺描述

T恤的衣袖轨迹如图1所示。其轨迹就是把袖片和衣片连在一起，将腋下接缝处和肩缝处对齐，袖孔包住筒状袖片，由于袖山弧线与袖窿弧线只有在空间某个位置才能重合，所以采用包缝工艺进行空间立体缝纫。为满足立体缝纫的动作要求，首先需要有撑布的动作，将衣片和袖片撑成空间立体形状进行空间弧线拟合，因为袖片整体近似为圆台形，所以撑布动作需要机构有2组绕杆轴转动动作，分别来完成袖片和衣片的撑紧。在缝纫过程中如果缝纫轨迹与弧线有偏差，需要进行纠偏，纠偏动作需要沿着连杆方向进行移动来完成袖片的位置调节。所以根据立体缝纫的工艺要求，该机构需要至少1个转动自由度和1个移动自由度来完成立体缝纫的撑布和纠偏动作。

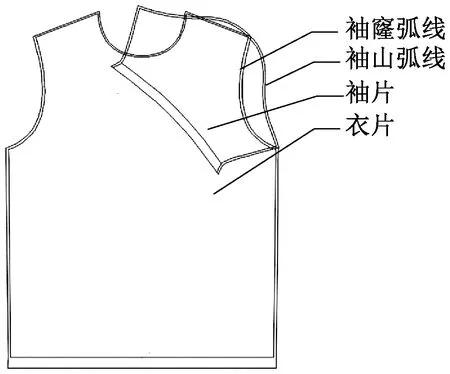
图1 T恤衣袖轨迹示意图

1.2 随形机械手机构设计

根据1.1节的工艺要求，随形机械手机构需至少具备2个自由度，来完成衣袖过程中的撑紧和纠偏，由于袖片属于空间近似对称形状，所以自动衣袖过程也近似为对称缝纫的过程。为简化自动化缝纫的控制流程，本文设计为偶数组空间对称的2自由度的平面机构来完成空间撑布过程。以2XL的T恤作为研究对象，其袖片周长约为560 mm，如图2所示。

图2 袖片尺寸图

将袖片进行若干等分，将等分点依次对齐，测量袖片和衣片之间的误差，如图3所示。将袖片2等分时，袖片和衣片的误差为39 mm；将袖片4等分时，误差为9 mm；将袖片6等分时，误差为5.5 mm；将袖片8等分时，误差为1 mm。

图3 袖片等分误差图

通过实验证明，8等分之后的袖片与衣片的拟合度最高，所以4组连杆机构是能够使袖片和衣片空间拟合的最少组数。

根据工艺需求分析，本文设计了一款空间结构对称的4-HPP6R随形机械手，如图4所示。该机构由静平台和4组支链构成。由于每组支链结构相同、参数类似，所以本文只分析其中1组支链，其他支链的分析方法相同。该机构每组支链都是1组平面连杆机构，其机构示意图如图5所示。螺旋副O1为驱动副，驱动各个支链进行空间转动，旋转副Ai、Bi、Ci(i=1，2)均为连杆机构的转动关节，移动副Mi(i=1，2)为驱动副，驱动面料沿着支链方向进行移动，所以通过驱动螺旋副和移动副能够改变各支链末端的空间位置。

图4 4-HPP6R随形机械手三维示意图

图5 平面连杆机构示意图

1.3 自由度分析

根据Grüler_Kutzbach公式，自由度计算公式为

(1)

式中：λ为机构的阶数；n为活动构件数；p为运动副数；fi为第i个运动副的自由度数。

由于分析的机构为平面连杆机构，所以阶数为3，活动构件共有7个，运动副数为9个，且运动副均为自由度为1的低副，该机构不存在虚约束，不存在局部自由度。所以该平面机构的自由度为

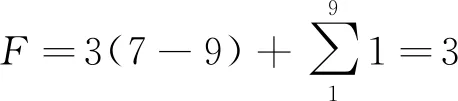
该平面连杆机构的每只手指都可以完成绕铰链转动和沿连杆方向移动2个动作，由于该机构为空间对称结构，有4组类似的结构组成，所以整体自由度为9。该结构中，螺旋副能够驱动连杆向外扩张，达到撑开面料的目的，每根连杆上的皮带移动副都可以通过正反转实现面料对应位置上的位置调节。

2 随形机械手机构运动学分析

2.1 位置分析

选取螺旋副作为内支链的驱动副，铰链的结构矢量图如图6所示。驱动距离为Ly；连杆O1B长度为L1，其与y轴夹角为β1；连杆AB长度为L2，其与x轴夹角为α1；连杆CD长度为L3，连杆O1C长度为L4，连杆AO的长度为LAO，连杆P1B的长度为LP1B。位置分析的目的在于建立驱动副与连杆末端的映射关系，设定末端点P1(Px1，Py1)和P2(Px2，Py2)。

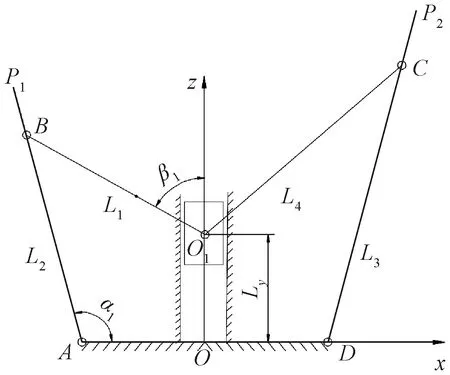
图6 铰链结构矢量图

(2)

将各矢量分别向x轴和y轴进行投影，得到

(3)

由式(3)可得

(4)

内部铰链的P1点坐标可表示为

(5)

2.2 速度与加速度分析

将式(3)分别对时间求导，得到速度关系：

(6)

进而得出转角β1和α1的转角速度φ1和ω1分别与驱动速度vy的关系为

(7)

将式(6)分别对时间求导，得出转角β1和α1的转角加速度分别与驱动加速度的关系，结果近似为0。

机构的设计参数如下，LOA长度为98 mm，L2长度为100 mm，L1长度为110 mm，Ly为一个变动量，即

Ly=85+vt

(8)

式中：v为电动机的驱动速度，mm/s；t为装置的运行时间，s。

电动机速度调整为10 mm/s，时间取8 s，将上述参数代入到MatLab软件中进行仿真运算，结果如图7所示。通过对机构进行运动学仿真，可以得到不同驱动速度与转角的三角函数值的对应关系，进而找到驱动参数与目标位置的函数关系。

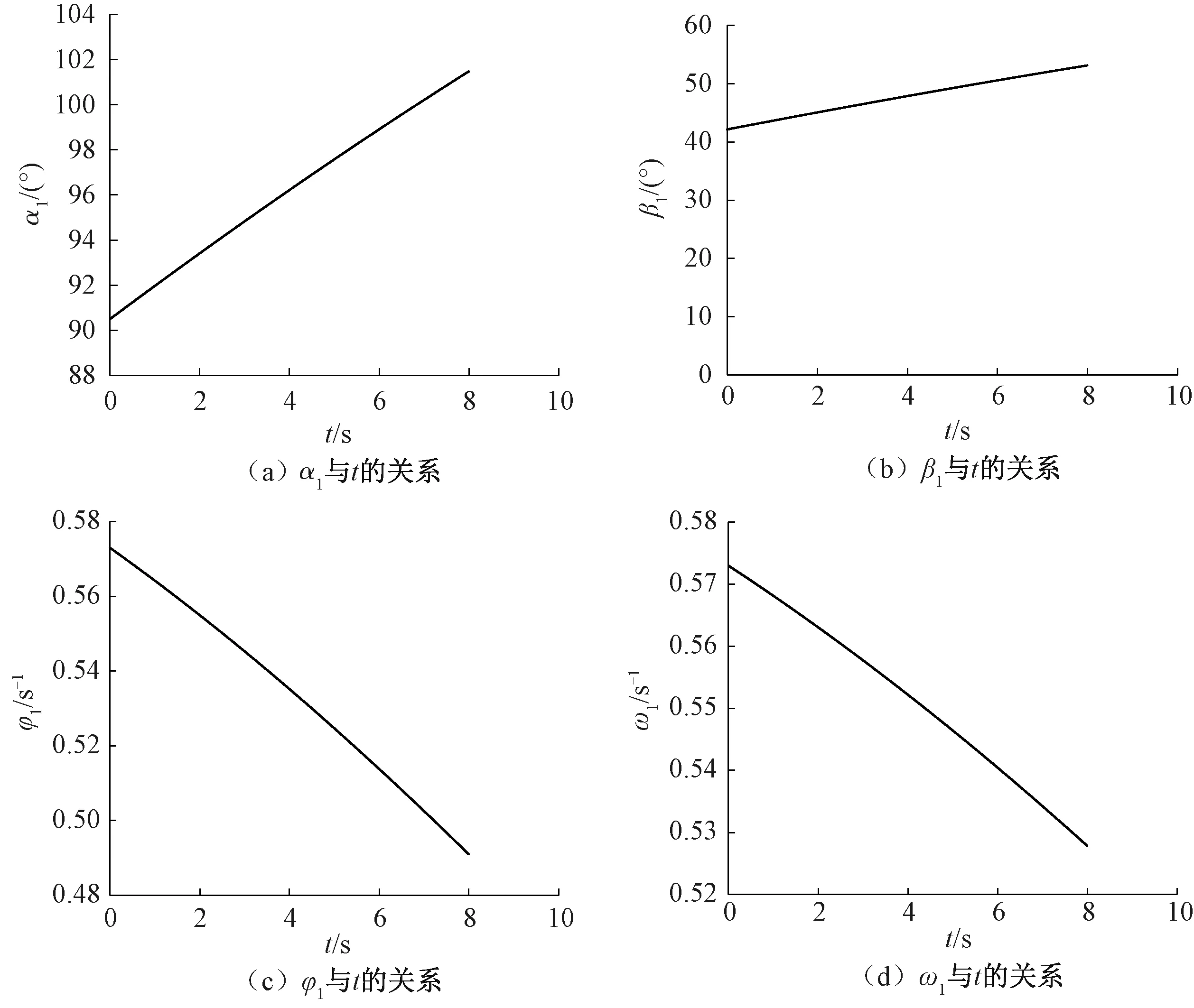
图7 连杆结构运动规律曲线图

2.3 工作空间分析

取t范围为(0，8)代入式(4)和(5)，得出机械手手爪的工作空间，基于蒙特卡洛法通过MatLab求得手爪的工作空间，如图8所示。该结构能够撑起袖口直径为200～260 mm的袖片。

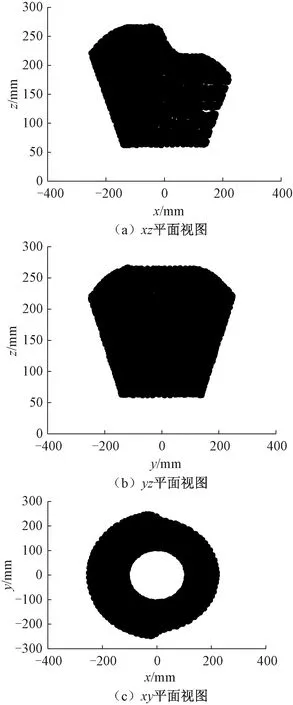
图8 机械手爪工作空间

3 力学和单指可调范围分析

将机械手手爪调整面料位置的过程做力学分析，如图9所示。由于8根手指的结构相同且对称，所以只分析其中1根，其他分析过程类似，不再赘述。

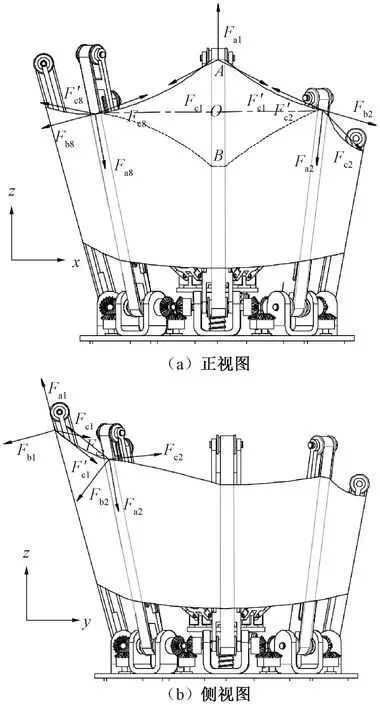
图9 机械手爪受力分析图

当面料套进手爪内，手爪在调整面料位置的过程中会对其产生一定的动摩擦力Fa，方向与手指调整方向一致；与调整手指相邻的2根手指不动，会对面料产生一定的静摩擦力Fc，方向沿着面料边缘方向指向相邻手指两侧，分别记作F′c和Fc；由于整体手指结构近似为等八边形，所以手指对面料有向外的支撑力Fb。由于面料具有弹性，所以手指在动作过程中会使面料有一定的弹性变形，当弹性变形达到最大值时，四者在空间会存在2处受力平衡点A和B，此时的受力方程为

(9)

Fb=Fcos(α1-β1)

(10)

(11)

两侧手指到调节手指的距离为a，则单个手指的调节范围为

(12)

将袖片套上去之后，袖片与手指的交叉线作为基准线，然后向上调节的范围记为L上，向下调节的范围记为L下，实际的调节范围就是L上+L下，如图10所示。

图10 单手指调节过程

与理论计算的数据做对比分析，纯棉面料与硅胶材质的表面摩擦因数为0.42[16]，纯棉面料的弹性系数约为1.25 N/mm[17]，测试得到手指与面料之间的压力结果如图11所示。可知，当手爪撑布稳定之后，连杆测试的压力F值约等于8 N，然后将参数代入式(10)～(12)，得出单手指上下调节的理论范围为±20.7 mm。

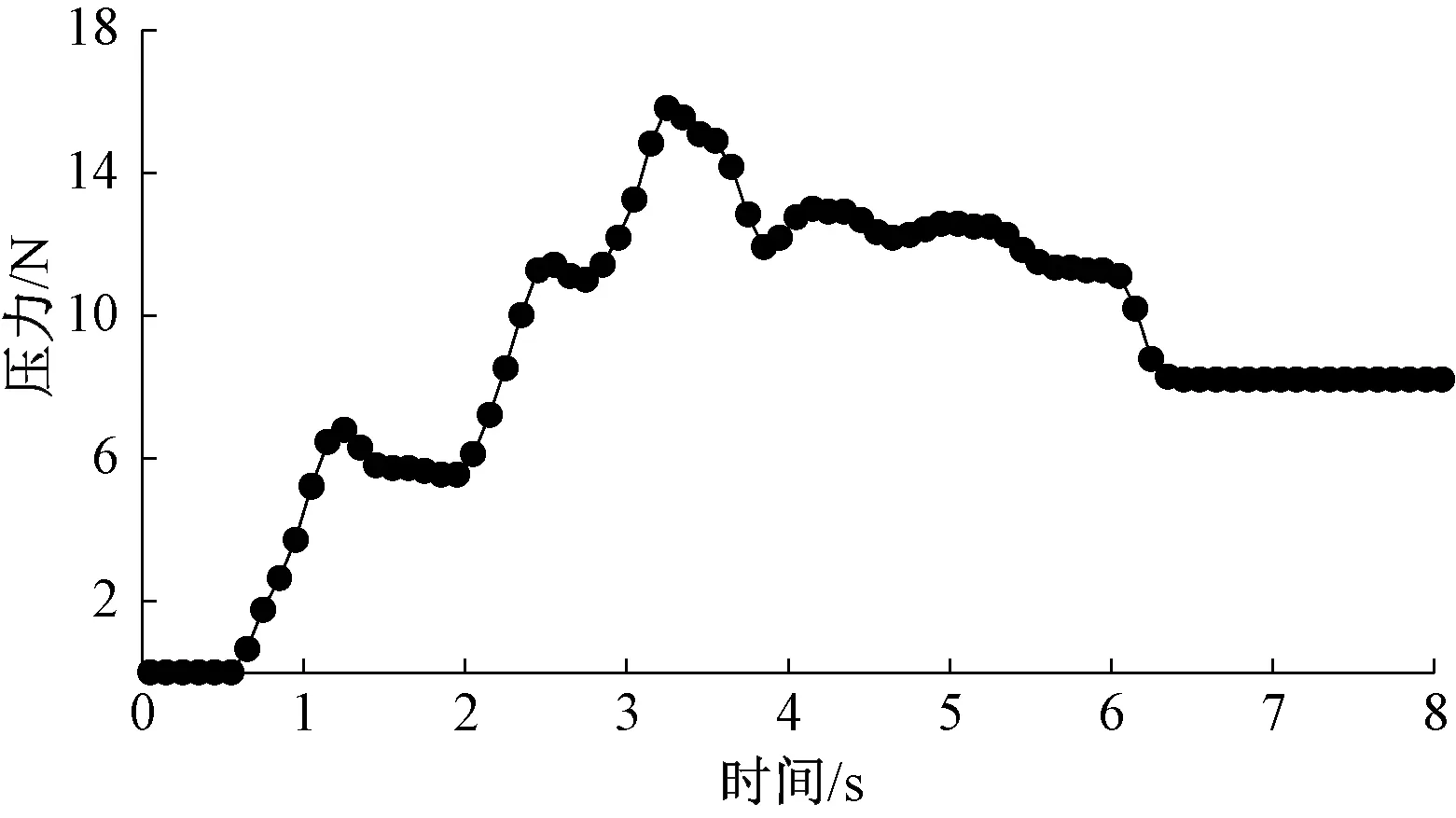
图11 压力与时间关系图

4 实验设计及验证

搭建如图12所示的机械手硬件平台。该平台主要由控制模块和执行模块组成。控制模块主要由西门子1200系列可编程逻辑控制器(PLC)、电动机驱动板和信号转换板组成，执行模块主要由驱动电动机、同步带和同步轮，以及连杆机构组成。

图12 机械手实验平台

减速电动机的额定输出转速为120 r/min，控制系统由PLC通过脉宽调制(PWM)的控制方式控制电动机转速。主从同步轮的齿数相同，均为18齿，节距为3 mm。设定面料的移动速度为v面料，电动机的转速为v电动机，同步轮直径为d，则面料进给速度为

v面料=v电动机πd

(13)

控制电动机转速为40 r/min，则面料的进给速度约为41.9 mm/s。设计实验每隔0.1 s进行1次调试，对比理论调试范围和实际调试范围的误差值，结果如表1所示。

表1 手爪单指调节精度实验结果

由表1可知，向上调节过程中，由于两侧手指对面料的拉力，在0.5 s时实际值与理论值的误差已经达到4.8 mm，且调节的实际位置与0.4 s的位置相差仅为0.1 mm，所以单手指向上调节的最大范围为16.8 mm。同理，在向下调节过程中，在0.4 s时面料的实际位置与理论位置误差已经达到4.5 mm，且与0.3 s时的位置相差0.2 mm，因此，单手指向下调节的最大范围为12.6 mm。综上所述，机械手的单手指实际调节范围为-12.6～16.8 mm，超出该范围调节误差将会明显增加，不再具有实际调节意义，在该调节范围内最大误差率为4.34%，最大误差值为0.70 mm，根据实际缝纫工艺的技术要求[18]，缝纫误差小于2 mm即可满足实际应用，所以该调节精度能够满足缝纫要求。

5 结 论

1)本文提出一种用于柔性面料立体缝纫的随形机械手结构，通过蒙特卡洛法分析，利用MatLab仿真得出了机械手的工作空间，能够完成对袖口直径为200～260 mm袖片的撑布操作，通过力传感器的信息反馈完成对面料的自适应控制。

2)通过实验分析，本文所提出的机械手结构具备缝纫过程中自动纠偏的能力，通过力学分析和实验验证得出单手指的调节范围为-12.6～16.8 mm，最大误差率为4.34%，最大误差值为0.7 mm，可满足实际缝纫需求。