列车端部吸能装置稳态阻抗力优化设计
吕天一,肖守讷,朱 涛,张敬科
(西南交通大学 牵引动力国家重点实验室,四川 成都 610031)
在列车的碰撞过程中,保证乘员生存空间与降低碰撞加速度的关键在于碰撞能量的吸收。通过在列车端部加装吸能装置以及在车辆端部设置可变形吸能区,可以与车钩组成以多级吸能为基础的碰撞能量管理体系。相关列车对撞试验表明,碰撞能量管理系统能够极大提高列车的碰撞安全性[1-3]。经过碰撞能量管理改装的列车,碰撞过程中其轮轨抬升量会大幅下降,在降低了爬车、脱轨可能性的同时,使更多的能量由吸能装置、车钩等吸收。由于列车碰撞试验的费用高、复杂,之后的研究更多通过仿真与简化模型的手段进行。文献[4]分析了碰撞安全性标准对吸能装置的吸能量要求,并建立了列车纵向碰撞模型,据此提出了端部吸能装置的经验公式。文献[5-6]等通过简化某型意大利列车,建立了列车纵向碰撞动力学模型,使其能够分析列车参数对纵向冲击的影响。文献 [7]把通过试验测得的力-位移曲线输入列车纵向碰撞动力学模型之中,取得了与试验结果吻合较好的动力学结果,这也表明了建立纵向碰撞模型研究列车的响应是比较可靠的。文献[8]等研究了碰撞场景下列车的响应,建立了列车纵向-垂向碰撞动力学耦合模型,得到了比较理想的仿真效果。文献[9]等通过建立列车纵向碰撞动力学模型,对列车能量配置方案进行动力学仿真计算与对比分析,得到了较好的能量配置方案。通过对列车碰撞动力学的不断深入研究,可以将更为复杂的动力学模型进一步应用到碰撞安全性的领域中。
虽然列车纵向碰撞动力学模型不能精确地反映车辆局部的运动与变形,但在车辆被动安全结构设计以及现有车辆的被动安全系统改装时,可以为结构的碰撞能量吸收分配提供一种快速而足够精确的手段。端部吸能装置作为车辆被动安全系统的重要部分,在碰撞过程中将承担主要的吸能任务。在车辆和车钩参数确定的情况下,通过分析列车的碰撞响应过程,从列车的速度与能量关系的角度,可以预测吸能装置的吸能量。文献[10]研究了车辆撞击刚性墙的响应过程,通过对比试验数据发现,头车的加(减)速度承受水平要明显大于随后的车辆。因此对车辆端部吸能装置及车钩的阻抗力进行优化设计有比较重要的现实意义。以此为基础优化设计吸能装置的阻抗力,可以使列车的被动安全系统协调运作,从而为车辆的设计和改造提供理论基础。
1 列车纵向碰撞动力学模型
为了模拟碰撞场景下列车的响应,将车体视为刚体,由非线性刚度的弹簧代替钩缓装置与吸能装置,可以建立列车纵向碰撞多刚体模型[4,11]。
在结构设计过程中,吸能装置的阻抗力不能无限增大。若阻抗力接近或超过车体端部吸能区的刚度,则会失去多级吸能的效果。因此在动力学模型中应当体现出车体的弹-塑性特性,参考文献[12]建立的车钩的力-位移曲线见图1。
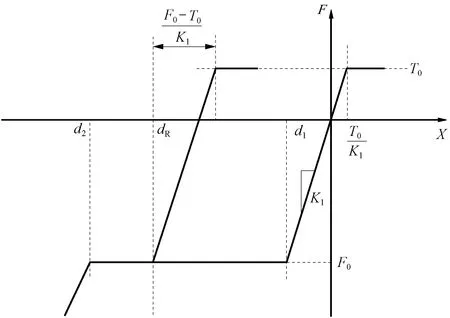
图1 理想弹-塑性力位移曲线
(1)
式中:F为阻抗力;F0为稳态压缩阻抗力;T0为稳态拉伸阻抗力(对于吸能装置等不承受拉力的单元,其T0设为0);K1为弹性段刚度;d1为弹性极限;d2为硬化点;dR为卸载点。作为优化设计目标的稳态阻抗力均为F0。
以此为基础建立的列车纵向碰撞动力学模型见图2。
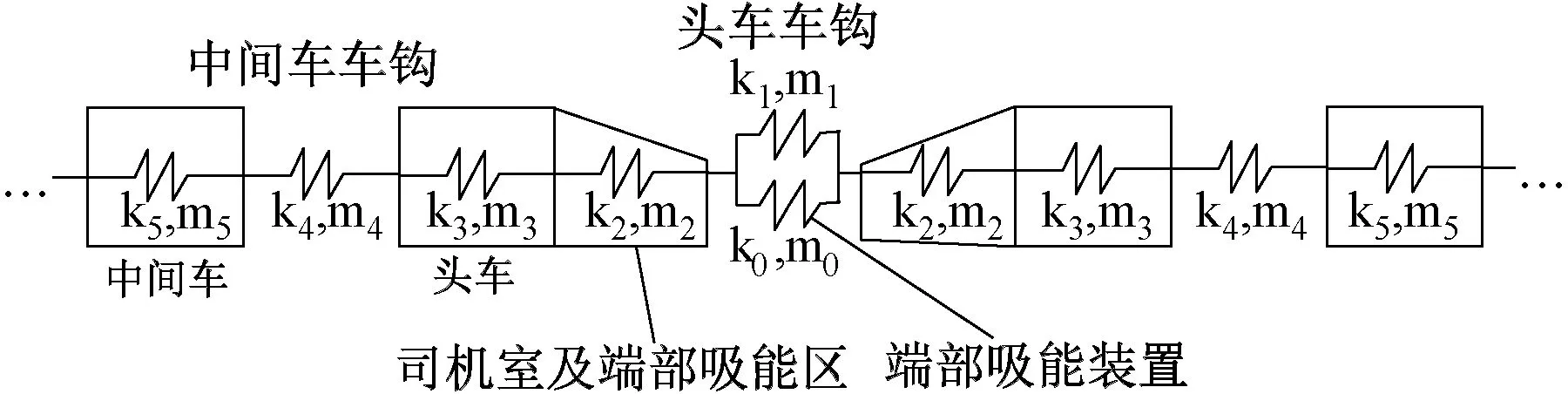
图2 带端部吸能区的改进模型
采用集中质量矩阵将单元质量分布到两侧端点处建立列车纵向离散模型,得到了与多刚体模型类似的非线性方程组为
Ma+Ku=F
(2)
式中:M为单元质量矩阵;a为节点加速度列向量;K为单元刚度矩阵;u为节点位移列向量;F为节点外力列向量。
2 端部吸能装置的设计理论
2.1 吸能装置实际吸能量的上限
列车端部吸能装置通常与推回式车钩共同使用以达到更佳的吸能效果。推回式车钩会在达到最大行程时剪断并回推以防止爬车现象。在碰撞过程中,两侧头车车钩首先接触,车钩缓冲器和压溃管吸能,当达到最大行程时螺栓剪断,车钩退回到底架内部,此时车钩不再提供阻抗力。随后端部吸能防爬装置接触并压缩吸能,在行程用尽后两车端部吸能区接触。某四编组的列车对撞场景见图3。图3中,A列车为主动车,以25km/h的初始速度撞击B列车,B列车静止于轨道上,两车均无制动。主动车从碰撞界面的车辆起,向远离碰撞界面的方向依次命名为A1车、A2车等,被动车依次命名为B1车、B2车等。A1车与A2车之间的界面命名为A1-A2界面,A1车与A2车之间的车钩称作A1-A2车钩。

图3 两列4辆编组的列车对撞场景
分别设置由小到大的10组端部吸能装置阻抗力,利用带端部吸能区的改进模型,以文献[13]进行数值积分求解。
计算结果见图4。列车碰撞安全标准BS EN 15227—2019中明确规定碰撞过程中的最大平均加速度是保护乘员安全的关键指标[14]。其最大平均加速度按照标准中的计算方法得到。主动车和被动车端部的吸能装置完全相同,其行程之和为0.8m。

图4 吸能装置采用不同阻抗力时车辆的碰撞加速度、各部件的变形量和吸能量
端部吸能装置作为可替换部件,在设计中应使其尽可能多地吸收能量以保护其他部件。碰撞过程中一旦吸能装置的行程全部压缩后车体端部吸能区即会发生变形。
分析以上列车的被动安全系统各指标,发现当吸能装置阻抗力取一个较低的值(图4(c)中为200kN)时,吸能装置已完全压溃,车体端部吸能区发生碰撞,使碰撞加速度处在较高的水平。随着吸能装置的稳态阻抗力逐渐上升至约800~1 000 kN之间,车体端部吸能区吸能逐渐下降,车辆碰撞加速度也逐渐下降。当阻抗力继续提高时,车体端部吸能区不再参与碰撞吸能,吸能装置已压缩行程从最大值开始下降,车辆碰撞加速度逐渐上升。表明随着吸能装置稳态阻抗力的提高,车辆碰撞加速度呈先降低在升高的趋势。分析其原因,当端部吸能区参与碰撞,其刚度高于端部吸能装置,则必然导致较高的加速度;而吸能装置压缩行程过低时能量吸收占比过低,从而不能起到保护作用。根据分析结果可以得到初步的结论,即最优的阻抗力设计应使碰撞过程中吸能装置压缩行程尽量接近吸能装置全行程,但不要超过全行程。下一步的数值设计依据这一结论,通过吸能装置压缩行程等于全行程求解最优阻抗力。
2.2 阻抗力优化设计流程
在碰撞过程中的吸能装置作用时段内,主动车的动能分别被头车吸能装置以及后车车辆间车钩缓冲装置所吸收。该时段内车辆的响应是由车钩力与吸能装置阻抗力引起的响应叠加而成。因此吸能装置阻抗力引起的响应可由前两者之差得到,从而求得吸能装置引起的车辆系统吸能量的增量,这一增量由吸能装置吸能量的增量和车钩吸能量的增量两部分组成,最后可以得到吸能装置实际吸能量,使最优阻抗力问题转化为列车速度响应的求解见图5。
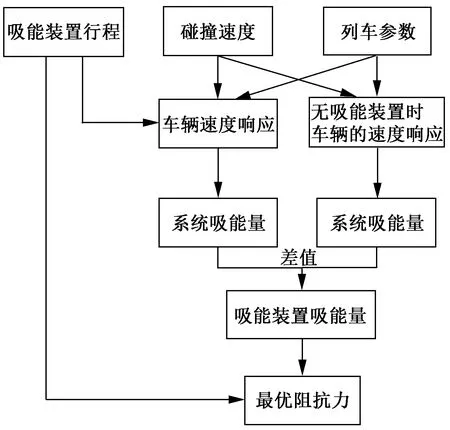
图5 阻抗力优化设计流程
3 阻抗力的数值设计
3.1 对某列车碰撞响应的分析
在2.1节所述4编组列车对撞场景下的某碰撞速度响应示意见图6。图6已将两列车头车达到相同速度之前的阶段分为a、b、c三段区间。区间a从头车车钩接触时刻开始,至车钩剪断时刻结束。此区间头车受力为头一位端的车钩阻抗力。由于头车和随后的中间车位移差较小,此时二位端中间车钩界面力较小。区间b从头车车钩剪断时刻开始,至吸能装置接触时刻结束,区间内头车只受到其二位端中间车钩界面力作用。区间c为吸能装置作用区间,端部吸能装置主要吸能区间为c区间。车钩缓冲器和吸能装置之间必须设置空行程,由于空行程的存在,使头车一位端向后的阻抗力消失,导致头车出现反向加速度,b区间的物理意义即是由空行程引起的反向加速区间。车钩缓冲器通常在碰撞速度大于连挂速度(一般小于10km/h)时螺栓剪断并退回,在BS EN 15227—2019[14]碰撞安全性标准中规定的设计碰撞速度25~36km/h下,车钩缓冲装置压溃,进而触发车钩剪断和通过空区间是车辆碰撞吸能的必要过程。因此形成分区是必然结果,与设计碰撞速度无关。

图6 碰撞过程中两侧头车的速度响应
由于两侧列车是完全对称的,以下将只考虑主动车。在区间c结束时,A4及之后的车辆速度变化量较小,因此在每个区间内,提出了如下简化方法:
(1)区间a:除A1车以外的车辆速度维持不变,忽略中间车钩吸能。
(2)区间b:除A1、A2车以外的车辆速度维持不变。
(3)区间c:A4及之后车速度维持不变。
基于以上简化方法,认为每个区间车辆内加速度不变,得到列车的实际简化速度响应见图7中实线。未装吸能装置时,列车的响应见图7中虚线。车辆的速度响应可视作由车钩引起的响应与由吸能装置引起的响应叠加而成,即图7中虚线与实线的差值即为吸能装置引起的响应。

图7 简化的速度响应
3.2 端点速度求解方法
基于区间a基本假设,该段A1及B1车损失动能即等于头车车钩剪断后的总吸能量。得到
ΔEkA1+ΔEkB1+WCoup1=0
(3)
式中:ΔEk为动能变化量;WCoup为车钩吸能量。
将初始速度v0代入式(3),可得
(4)
式中:va为车辆在区间a末端的速度;m为车辆质量。
将区间a的位移作为区间b的初始条件,但该位移值较小,且初始位移对区间b最终速度影响较小,因此采用匀加速运动估计区间a位移xa。
(5)
式中:ta为区间a耗时。
以两列完全相同的列车为研究对象,可视作两列车的速度响应是对称的。基于列车纵向动力学模型及其简化模型,将主动车A1-A2视为两自由度振动系统,A3速度不变,采用以A3为参照点的相对坐标系,建立系统振动方程为
Kx+Ma=0
(6)
得到响应为
v(t)=
(7)
式中:K为列车刚度矩阵;M为列车质量矩阵;u(r)为系统固有振型;ωr为系统固有频率。

(8)
vbA1=vA1(tb)
(9)
以匀加速假设估计区间c耗时tc得到
(10)
将区间c的响应由两部分叠加而成:由头车车钩剪断引起的响应与吸能装置引起的响应。前者仍然使用式( 7 )计算。由于两列车是对称的,该叠加响应使两侧头车在tc时刻速度相等,为初始速度的一半。
将阻抗力视为外加恒力激励,则吸能装置阻抗力引起的响应为
(11)
假设头车与中间车质量相等,由式(12)可得吸能装置阻抗力引起的A1与A2车速度响应比值α,并估计A2车在区间c结束时刻的速度为
(12)
若采用三自由度模型计算A3车速度响应,则只能采用数值积分算法。考虑到中间车及中间车钩的质量、刚度等近乎相同,在区间c的极短时间远小于A3车的响应周期,以A1与A2的响应之比α代替A2与A3的响应之比,得到A2车与A3车的速度响应为
(13)
(14)
由式( 3 )~式(14)可估算各车辆在每个区间的端点速度。
3.3 最优阻抗力的计算
由式(14)解出tc时刻A2车速度响应,则可解出此时实际车辆间位移x与仅有车钩响应下的位移x*。由该两项可以得到实际响应的车钩吸能量与仅有车钩响应下的车钩吸能量,两者之差即为车钩吸能增量为
(15)
(16)
(17)
由于列车响应的对称性,两侧车辆的速度变化量相反,车钩吸能量相等,由此可得
(18)
(19)
(20)
端部吸能装置的总吸能量即为式(15)~式(20)所求解吸能量之和,可以表示为
(21)
吸能装置的稳态阻抗力决定其吸能容量,使理论设计吸能容量等于预测的实际吸能量即可求得此场景下的最优吸能装置稳态阻抗力为
(22)
式中:xc为端部吸能装置的全行程。
4 算例验证
为了验证模型简化以及设计计算的可靠性,将设计阻抗力代入车辆模型中,与吸能装置阻抗力设置为不同数值的其他模型仿真结果进行对比。根据标准BS EN 15227—2019[14]对碰撞场景和碰撞速度的要求,对于不同场景下的相同类型的编组前端对撞,试验碰撞速度设置为36、25km/h。因此分别在这两个速度等级下求解模型,从而对上述设计方法在不同速度等级下的适用性进行补充。以某市郊线路的8编组列车对撞为例进行对比,该列车的参数见表1。表1中所列头钩与吸能装置参数均为一对的数值,即两侧头车对应装置串联。
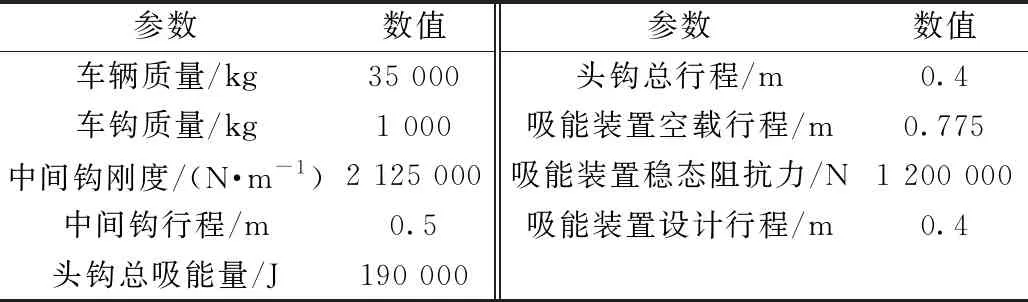
表1 某列车相关参数
两列车除吸能装置稳态阻抗力之外的参数全部相同,原列车的吸能装置阻抗力为1 200 000N,优化设计后的吸能装置稳态阻抗力为976 013N。优化设计后列车吸能装置吸能量与最大平均加速度与原配置的对比见表2。由表2可见,对吸能装置稳态阻抗力进行优化设计后,列车碰撞安全性有了较大幅度的提高。

表2 优化设计前后的相关指标对比
将优化设计的吸能装置稳态阻抗力作为基准,与其增减±10%、±20%的五个吸能装置阻抗力输入纵向动力学模型求解并进行对比。一共设置两组不同速度下的碰撞场景,主动车速度为6.944 m/s(25km/h)、10.000 m/s(36km/h)。输入的吸能装置阻抗力见表3。
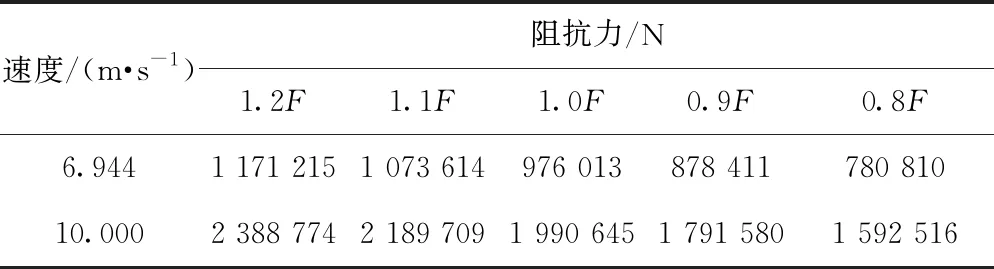
表3 两种碰撞场景下的输入吸能装置阻抗力
每种碰撞速度场景下,不同的吸能装置的理论容量和实际吸能量见图8。
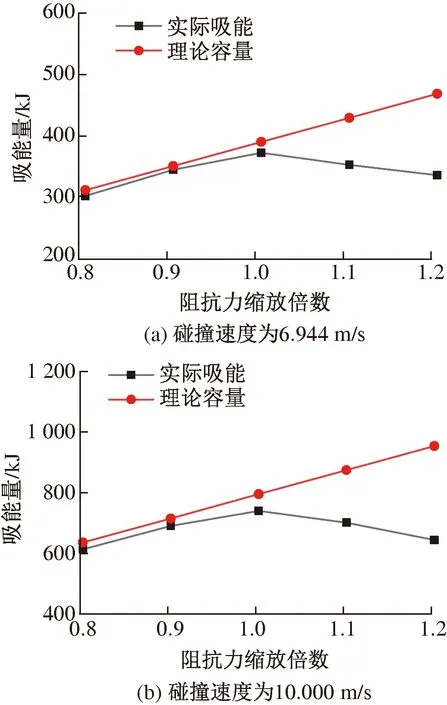
图8 碰撞速度为6.944、10.000 m/s时设置不同阻抗力的吸能装置吸能量对比
由图8可见,随着吸能装置稳态阻抗力的上升,端部吸能装置的吸能容量也随之上升,在阻抗力到达某一临界点(即优化设计的最优阻抗力)时,阻抗力的上升会使吸能装置的实际吸能效果下降。在吸能装置的阻抗力过小时,吸能装置容量以及保护效果有限,不能吸收更多的能量。
优化设计后的吸能装置在各个速度场景下的实际吸能量均为本组最大值,可认为基于动力学模型的简化方法在标准规定的速度等级下对吸能量结论的影响较小,同时设计计算的可靠性较高。列车吸能装置阻抗力在重新设计后,其已压缩行程占比过90%,具有较好的经济性。
5 结论
对列车端部吸能装置阻抗力的优化设计,得到了以下结论:
(1)在列车参数、行程、碰撞速度确定时,列车端部吸能装置的吸能量随着其稳态阻抗力的上升呈先上升后下降的趋势,其吸能量存在最大值,且此值出现于碰撞中吸能装置已压缩行程等于全行程时。过小的稳态阻抗力使吸能装置的最大吸能容量变小,降低防撞能力。过大的阻抗力使碰撞过程的加速度变大,同时降低了其容量利用率。
(2)通过对碰撞动力学模型的分析以及简化,可以得到由吸能装置引起的车辆速度响应解,进而求得由吸能装置引起的系统吸能量的增量,此增量由吸能装置吸能量的增量和车钩吸能量的增量两部分组成,从而可以得到吸能装置实际吸能量,进而计算得到理论最优的阻抗力。
(3)通过对某列车进行优化设计发现,各速度下其优化设计后的吸能装置吸能量均大于对照组的吸能量,验证了分析及简化设计过程的可靠性。相较于原配置,经过优化设计后的吸能装置吸能量提高了39 kJ,提升幅度为11.73%,最大平均加速度下降了5.390m/s2,下降幅度为20.40%。

