直流电弧炉无功超短期滚动预测及控制
周 文 ,苏 灿 ,高 敏 ,朱明星 ,李铁成 ,孟 良
(1.国网河北省电力有限公司电力科学研究院,石家庄 050021;2.安徽大学绿色产业创新研究院,合肥 230601;3.安徽大学电气工程与自动化学院,合肥 230039)
电弧炉是典型的大功率冲击性负载,产生的冲击性无功对电网的电压波动和闪变产生严重的影响。为抑制电弧炉负荷对配电网电能质量的影响,在电弧炉中压系统均配置了动态无功补偿装置。虽然采用H桥级联技术的中压链式SVG已得到广泛应用,但由于控制算法复杂,在电弧炉配电系统成功应用的案例较少[1-2]。目前,电弧炉系统仍以TCR型SVC方案为主。
SVC装置对电弧炉系统电压波动和闪变的抑制效果,与TCR响应时间密切相关。根据文献[3-6]给出的不同响应时间下SVC装置的η-c特性曲线,当SVC补偿率C=100%时,在响应时间t=10 ms时闪变改善率为50%,t=20 ms时闪变改善率仅有15%,当t>20 ms时,SVC可能会增大电网中的闪变值。TCR采用晶闸管相控整流,响应时间一般大于10ms[1],闪变改善率一般小于50%,甚至小于35%[7]。因此采用SVC控制的电弧炉负荷,接入公共连接点时常出现闪变超标的问题。
采用无功预测控制可较好地弥补TCR响应时间上的缺陷。目前,预测技术在光伏发电功率[8-9]、风力发电功率[10-13],甚至是轧机系统无功功率[14]等方面得到广泛应用,但在电弧炉负载预测控制方面的应用相对较少。国内学者的研究方向,是将电弧炉模型预测应用于电极调节系统,对常规控制的电极调节器输出进行优化补偿,以获得更好的动态性能[15-17]。此外,部分学者基于混沌预测方法对交流电弧炉供电网波动电压进行了超短期预测[18],通过对交流电弧炉供电网电压时间序列进行特性分析并进行预测,以期解决电弧炉引起的闪变问题,但其仅处于预测方法研究阶段,未实现预测控制。国外学者中,仅有伊朗Shiraz大学的Haidar Samet针对交流电弧炉无功预测控制模型开展了相关研究[19-23],提出了基于随机过程、灰色系统、人工神经网络等模型的交流电弧炉无功预测方法,但其仅从数据统计指标角度进行了预测效果说明,并未对预测控制的动态跟踪能力、闪变改善情况进行分析,对预测控制算法优化和工程应用缺乏有效支撑。
随着大容量整流器件可靠性和稳定性提升,由于在吨钢电耗、电极损耗、噪音等方面的优势,直流电弧炉近年来又重新受到重视。直流电弧炉在控制原理和无功特性方面均与交流电弧炉存在显著差异,本文基于直流电弧炉电气控制原理,分析直流电弧炉无功特性,建立直流电弧炉无功功率超短期滚动预测模型,提出基于TCR型SVC的无功超短期滚动预测控制方法,并通过仿真分析验证预测模型及控制方法的有效性。
1 直流电弧炉工作原理及无功特性
大容量直流电弧炉设有弧压和弧流两个自动控制系统。弧压控制系统为电极升降控制系统,采用电压闭环控制,通过电极升降控制电极与废钢之间的弧长,进而稳定电压;弧流控制系统为整流控制系统,采用电流闭环控制,通过晶闸管整流移相角控制电流幅值,进而稳定电弧电流。直流电弧炉控制系统以工作点为控制基点,根据冶炼钢种确定不同时期的最佳电压、电流设定曲线,并将电压设定值UD,S和电流设定值ID,S分别送入电极升降控制系统和整流控制系统。电气控制原理如图1所示。
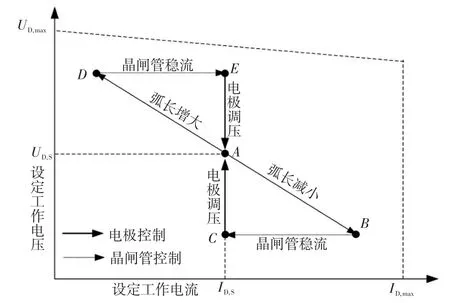
图1 直流电弧炉电气控制原理Fig.1 Electrical control principle for DC EAF
设定工作点为A点,电弧不同变化方向对应的控制系统动作过程如下。
(1)若弧长减小,弧阻和弧压降低,弧流ID增加,工作状态从A点转移至B点,此时弧流控制系统快速调整晶闸管触发角以稳定弧流,使ID=ID,S,即工作状态由B点转移至C点。由于C点弧压低于设定值UD,S,弧压控制系统通过电极调节器控制电极上升,弧长增加,工作状态又由C点回到A点。
(2)若弧长增加,弧阻和弧压增大,弧流ID减少,工作状态从A点转移至D点,此时弧流控制系统快速调整晶闸管触发角以稳定弧流,使ID=ID,S,即工作状态由D点转移至E点。由于E点弧压高于设定值UD,S,弧压控制系统通过电极调节器控制电极下降,弧长缩短,工作状态又由D点回到A点。
一般情况下,直流电弧炉在100 ms内即可完成一次弧流调节过程,但弧压调节过程往往要持续数百毫秒。以某130 T直流电弧炉为例,实测的一次完整的弧压和弧流调节过程如图2所示,对应的调节过程持续时间分别为920 ms和80 ms。

图2 直流电弧炉弧压和弧流调节过程Fig.2 Arc voltage and arc current regulation process of DC EAF
从控制效果看,快速的弧流调节过程,有利于稳定电弧电流,保持直流电弧炉视在功率的稳定性,有效改善电弧短路造成的大功率冲击。晶闸管在弧流调节过程中,触发角快速变化仍会导致无功功率的快速波动。实测的130 T直流电弧炉在一个通电周期内的三相总无功功率变化趋势如图3所示。
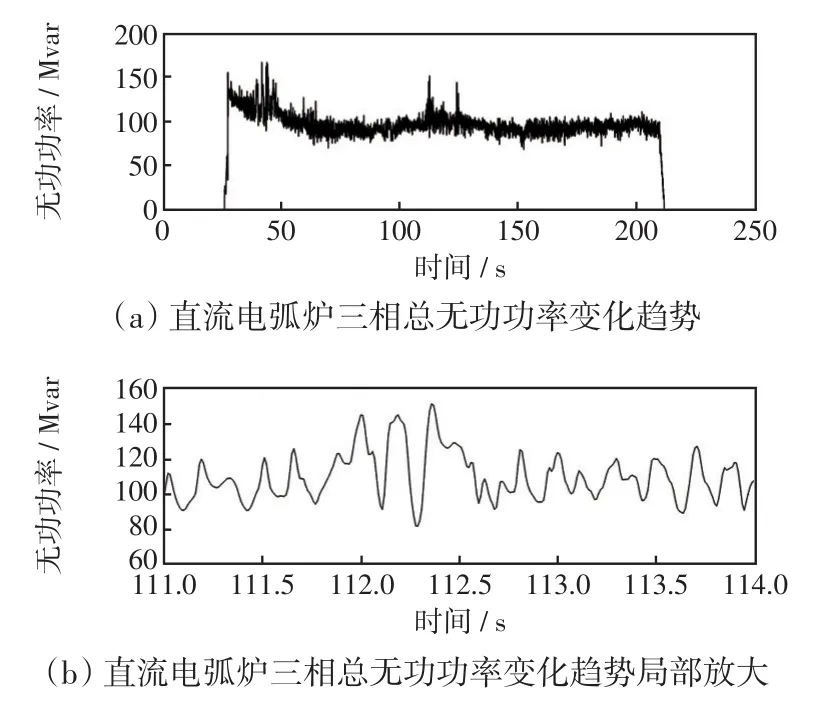
图3 直流电弧炉三相无功功率变化曲线Fig.3 Reactive power variation curve of DC EAF
由于设定工作点的约束,直流电弧炉无功波动具有一定的周期性,波动周期取决于弧压和弧流调节系统特性,一般在100~300 ms,且一个波动周期内的无功变化趋势具有一定的连续性,这为直流电弧炉ms级的超短期预测提供了可能性
2 预测控制方法
2.1 预测模型
直流电弧炉无功波动呈现一定的周期性,波动周期较短,波动速率具有一定的连续性,因此直流电弧炉在n时刻的无功功率不仅与n-1时刻的无功功率相关,而且与n-1时刻前的无功波动量(或速率)也存在一定的依存关系。因此可采用自回归移动平均ARMA(auto regressive moving average)模型对直流电弧炉无功功率进行超短期预测。ARMA模型是由自回归AR(auto regressive)模型与移动平均MA(moving average)模型构成,一般表示为ARMA(p,q),即

式中:等号右侧的前两项是AR模型,用变量自身的p阶历史数据进行预测,后一项是MA模型,关注的是前q阶扰动的影响;x(n)为n时刻的预测变量;x(n-i)为被预测变量相关滞后阶;φ0为常数项;ε(n-i)为扰动项;φi为自相关系数(i=1,2,…,p);θi为移动平均系数(i=1,2,…,q);p和q分别为自回归和移动平均过程中的滞后阶数,为控制计算量,一般限制p≤ 6,q≤ 4。
模型阶数会影响预测结果,阶数过高会造成计算量过大甚至过度拟合问题,阶数过低易出现局部最优问题,应用ARMA模型的关键是进行模型定阶。本文采用赤池信息准则AIC(Akaike information criterion)对预测模型进行定阶,AIC表达式为

式中:L为模型的极大似然函数;k为模型参数个数。当模型复杂度提高(k增大)时,L也会增大,从而使AIC变小,但是k过大时,似然函数增速减缓,导致AIC增大。因此,AIC较小的模型能够实现模型复杂度和拟合精度的权衡。
根据图3中实测的直流电弧炉无功功率趋势数据,采用AIC计算得到的模型最优阶数为:p=1、q=1,即直流电弧炉无功功率的最优预测模型为ARMA(1,1),则直流电弧炉预测模型的表达式可简化为
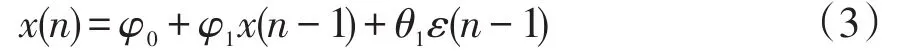
2.2 预测控制方法
传统SVC控制方法是基于补偿对象当前的无功需求量计算出TCR触发角,进而对当前无功功率进行动态补偿。由于TCR控制具有滞后性,传统控制方法难以满足对直流电弧炉无功功率的快速跟踪补偿,导致闪变抑制效果不够理想。而利用ARMA模型对直流电弧炉无功功率进行预测控制时,是基于当前的无功功率与扰动功率来预测下一时刻需补偿的无功功率,并将预测结果输出给SVC控制模块,实现超前控制,以弥补SVC响应时间的不足,提高闪变抑制效果。预测控制过程如图4所示。
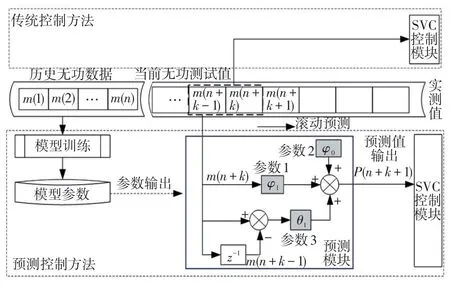
图4 预测控制主要实现过程Fig.4 Main realization processes of prediction and control
(1)无功功率数据处理。对直流电弧炉无功预测时,无功数据分析间隔应与预测时间尺度相匹配。用于SVC预测控制时,考虑到TCR响应时间,滚动预测时间应至少超前10 ms,无功计算间隔应不超过10 ms,本文采用10 ms分析间隔的无功功率进行预测控制。
(2)模型定阶和参数训练。通过信息准则判别和历史数据训练,确定合适的预测模型参数,再利用新的无功数据开展预测效果检验。通过检验,表明预测模型能够取得良好的预测效果,从而确定预测模型;若不满足检验结果,则继续优化预测模型。
(3)预测控制。将确定的预测模型及参数输入至SVC控制器的预测模块,预测模块的实现框图如图4所示,预测模块对直流电弧炉的无功功率进行超短期预测,并将预测结果输入至SVC控制模块,进而实现直流电弧炉无功超短期滚动预测控制。
3 算例验证
以图3中直流电弧炉无功数据为例,FFT窗口宽度为单周波,滑动窗口为半周波,得到分析间隔为10 ms的无功数据。利用30~140 s之间的数据进行模型参数训练,利用140~200 s之间的数据进行10 ms超短期预测效果验证,再利用25~225 s之间的数据开展SVC预测控制效果验证。
3.1 滚动预测效果
为分析不同模型阶数的预测结果,验证AIC的定阶效果,利用第30~140 s之间的无功数据,训练得到不同模型阶数对应的模型参数见表1。根据上述模型参数,对140~200 s之间的无功数据进行滚动预测,其中将199~200 s之间不同模型参数预测结果和实测值进行对比,如图5所示。
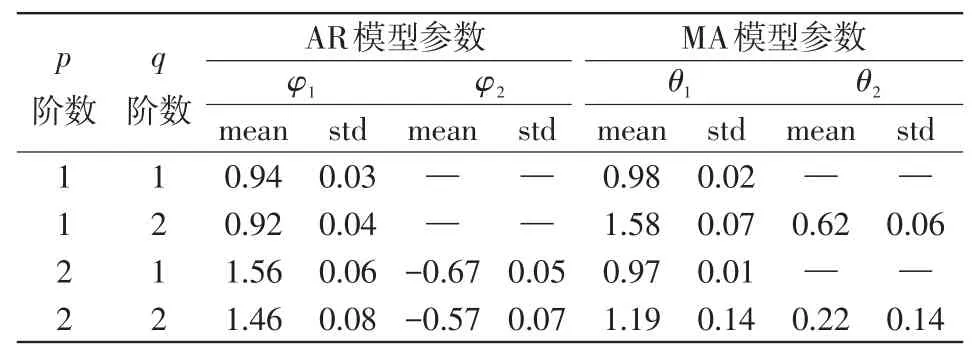
表1 不同模型阶数对应的模型参数汇总Tab.1 Summary of different model orders and parameters
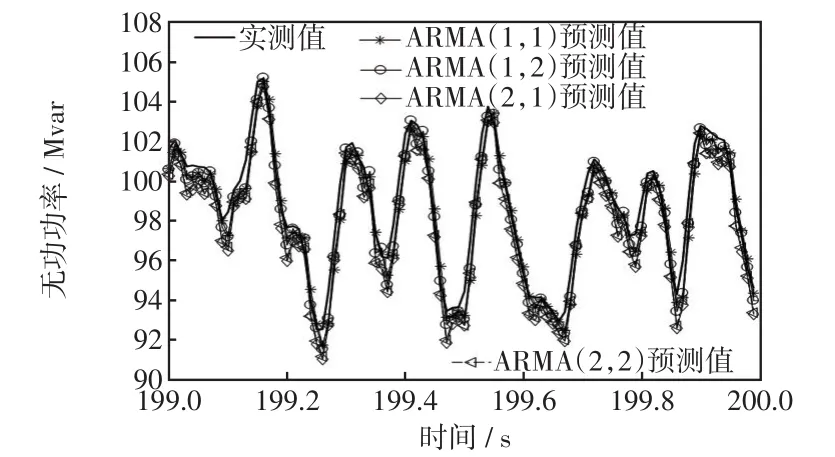
图5 模型预测结果对比Fig.5 Comparison of model prediction result
为评价不同模型阶数和参数下的预测精度,采用调整决定系数作为评价指标,即
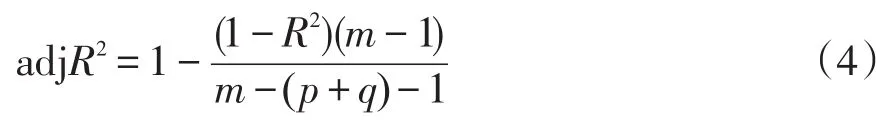
式中:adjR2为调整决定系数;m为样本总长度;R2为决定系数,其计算公式为

式中:yi为样本真实值;为样本平均值;为模型预测值。
adjR2的最优值为1,且取值越大拟合效果越好。一般认为,当adjR2>0.4,即可达到较好的拟合效果。不同参数对应的调整决定系数计算结果见表2,采用ARMA(1,1)、ARMA(1,2)、ARMA(2,1)、ARMA(2,2)模型开展直流电弧炉无功预测时的调整决定系数均大于0.96,远优于可接受阈值(大于0.4),即采用上述任一预测模型阶数均能取得较好预测效果。从预测精度考虑,采用ARMA(1,2)的调整决定系数更优;从信息准则角度,采用ARMA(1,1)的预测信息准则最小,因此,在模型复杂度和拟合精度之间的权衡更好。
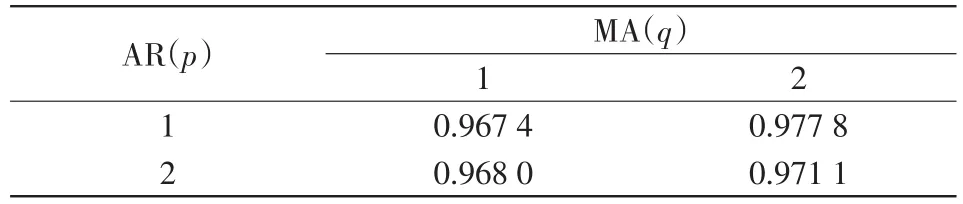
表2 不同模型阶数下的调整决定系数统计Tab.2 Statistics of adjR2 at different model orders
针对AIC判定的最优模型ARMA(1,1)开展预测残差检验,140~200 s之间的预测误差趋势如图6(a)所示,最大预测误差区间为[-7.44%5.56%]。根据图6(b)的Q-Q图,图中的点近似为一条直线,直线斜率为标准差(即σ=1),截距为均值(μ=-0.26),表明ARMA(1,1)预测误差近似满足标准正态分布,预测误差的95%置信区间为[-2.22%1.70%],平均值为-0.26%。
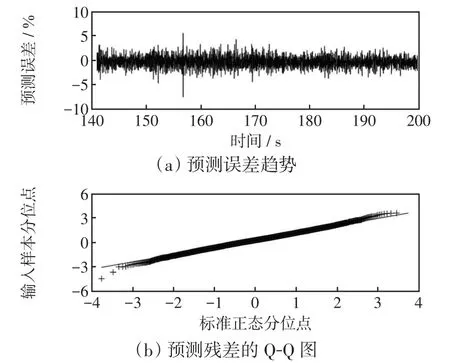
图6 模型预测误差分析Fig.6 Model prediction error analysis
3.2 预测控制效果
为验证预测控制算法对SVC装置的闪变抑制效果,建立含直流电弧炉和SVC补偿装置的配电系统仿真模型,其中220 kV系统短路容量为4 010 Mvar,供电变压器额定电压为220 kV/37 kV,额定容量为180 MV·A,阻抗电压14%,SVC容量为160 Mvar,仿真过程中直流电弧炉无功功率采用图3中25~225 s之间的数据,仿真步长为5×10-5s,分别对传统控制方法和预测控制方法两种策略下的闪变抑制效果进行仿真,得到的直流电弧炉35 kV母线瞬时闪变趋势,如图7所示。
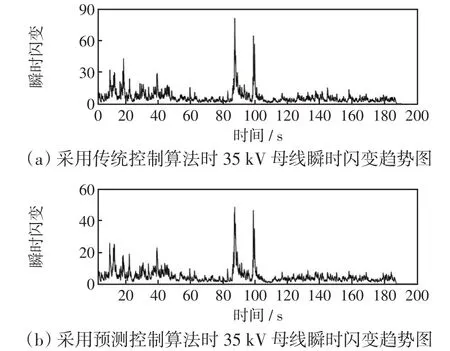
图7 两种控制策略下瞬时闪变趋势对比Fig.7 Comparison of instantaneous flicker trend under two control strategies
采用传统控制方法时,仿真得到的35 kV母线瞬时闪变最大值、95%概率值和平均值分别为81.26、15.66和6.04;采用预测控制方法时,对应的瞬时闪变统计值分别为48.42、10.78和4.41,比传统控制算法对应的瞬时闪变统计值分别下降了40.41%、31.16%和26.99%,预测控制算法对SVC装置闪变抑制效果改善显著。
在无功波动改善方面,在200 s的仿真过程中,2种控制策略对应的直流电弧炉35 kV总进线无功功率统计结果分别如表3所示。

表3 两种控制策略下35 kV总进线的无功功率统计Tab.3 Statistics of reactive power on 35 kV incoming line under two control strategies
采用预测控制后,直流电弧炉总进线最大感性无功功率由20.19 Mvar降至14.67 Mvar,最大容性无功功率由19.1 Mvar降至8.17 Mvar,最大无功冲击由39.29 Mvar降为22.84 Mvar,改善率达到24.05%。从统计特征上看,采用预测控制后,200 s内的无功功率数组标准差由3.52降至2.44,降低了30.7%,总进线无功功率波动得到明显改善。以图7中瞬时闪变最大时刻对应的无功数据为例,2种控制策略下SVC馈线与电弧炉馈线无功功率趋势对比如图8(a)所示。在电弧炉无功功率曲线拐点处,由于SVC装置补偿的滞后性以及拐点处预测误差增大,2种控制策略下的SVC补偿功率与实际无功需求的偏差均增大,但相较于传统控制方法,虽然在拐点处的无功补偿偏差略有增加,但预测控制输出的无功功率能够更快地响应电弧炉的无功变化情况,预测控制方法对功率冲击较大工况下的无功波动改善效果更加显著,如图8(b)所示。
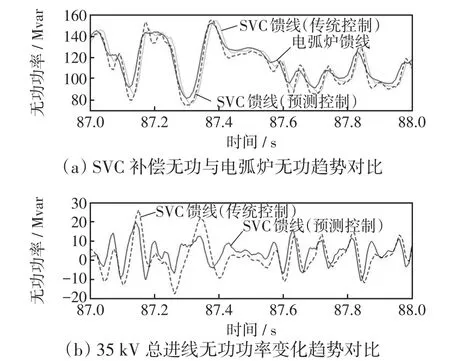
图8 两种控制策略下无功功率趋势对比Fig.8 Comparison of reactive power trend under two control strategies
为分析预测控制方法对SVC装置动态无功跟踪补偿能力,采用互相关函数计算2种控制策略下SVC装置无功补偿的延迟时间。2种控制策略下SVC装置输出的无功功率趋势和电弧炉无功功率趋势的互相关函数曲线如图9所示。采用传统控制方法时,SVC与电弧炉的无功功率互相关函数曲线最大值对应的延迟点数为228点,而采用预测控制方法时的互相关函数曲线最大值对应的延迟点数为76点。由于仿真的无功功率数据时间间隔为0.05 ms,可计算出传统控制和预测控制方法SVC输出无功功率的延迟时间分别为11.4 ms和3.8 ms,预测控制算法对SVC装置的动态无功补偿跟踪能力提升效果显著。
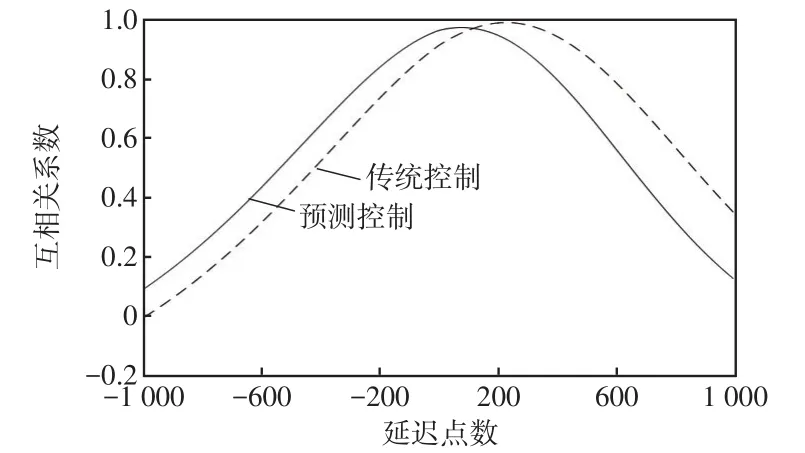
图9 两种控制策略下SVC和电弧炉无功功率互相关函数曲线Fig.9 SVC and EAF reactive power cross-correlation function curve under two control strategies
4 结语
针对直流电弧炉的无功特性,本文提出了基于ARMA模型的直流电弧炉无功超短期滚动预测控制方法,通过信息准则判定、历史数据训练和预测残差评价,采用ARMA(1,1)模型可实现直流电弧炉无功序列的超短期滚动预测,平均预测误差仅有-0.26%,预测误差的95%置信区间为[-2.22%1.70%],预测精度较高。加入预测控制算法后,SVC装置对直流电弧炉瞬时闪变最大值、95%概率值和平均值的改善率分别达到40.41%、31.16%和26.99%,对最大无功冲击的改善率达到24.05%,改善效果显著。

