兼顾微气象预警的输电线路人机巡检计划优化

欧阳森，陈义森

（华南理工大学电力学院，广州 510640）

随着电网的延伸发展，建设在复杂微地形的输电线路日益增多[1]，然而，在依据线路所处地形的巡视难度制定固定的巡检周期[2]时，未能充分考虑线路自身状态及所受微气象的影响。此外，为应对日益增大的巡检压力，无人机被广泛应用在输电系统中以提高巡检效率，但无人机对故障隐患的探查率低于人工[3]，而传统人工巡检发现缺陷能力强但耗时长，故对人机巡检进行合理分配成为提升线路巡检工作效率及质量的关键。

目前，国内外对电力设备巡检周期的研究较为深入，文献[4]基于维护变更成本对设备巡检计划进行优化，但将所有设备的故障概率视为等同；文献[5]基于缺陷数据计算设备故障概率，通过研究故障概率的变化规律确定最佳巡检时刻，并可计及个体差异，但未考虑不同设备故障对电网的影响程度；文献[6]从电网网架、系统运行方式及气候情况等多要素角度量化线路故障风险，并基于灵敏度分析实现线路的区别化运维；文献[7]将高压电缆划分为5部分，分别计算故障频率、设定故障修复时间与线路重要性计算各部分风险，实现不同组件的差异化巡检。然而，上述研究局限于巡检频率的改变，无法针对微气象突变来动态调整巡检任务；在巡检班组实际工作中，巡检时刻的提前和次数的增加也是巡检周期动态调整的一部分，从而不可避免地增大巡检压力。

为克服输电线路巡检工作量大和运维难度高等问题，文献[8]定义了由人工和各式无人机进行组合的15种巡检模式，并对巡检的综合效益及费用进行估算，但未针对人机巡检方式进行优化模型构建，巡检的效率和质量有待挖掘。

综上，线路巡检周期的研究未能依据微气象进行动态调整，人机巡检的效率及质量还有待提升。对此本文基于风险评估理论制定线路基础巡检周期；设计提前和额外巡检判定的流程；基于动态周期建立巡检计划优化模型；以某地区输电线路实例验证方法的有效性。

1 动态巡检周期制定方法

1.1 故障概率模型

动态风险评估的关键是求取输电线路的故障概率，其需满足的条件为①具有时变性；②可计及线路个体差异性；③可量化不同因素对线路故障概率的影响。文献[9]提出的比例风险模型可将故障时间分布与不同影响因素纳入统一框架进行描述，满足上述3个条件，但其仅考虑了老化因素及健康状态，本文对该模型进行拓展可得

式中：p(·)为输电线路的故障概率；λ0(t)为基准函数，用以描述线路基本的老化失效过程；Φ(·)为连接函数，用以量化不同因素对线路故障概率的影响程度，选取指数函数作为连接函数；t为线路服役年龄或等效运行年限；f1为线路整体长期运行工况的故障概率；f2为微气象预警对线路区段的短期故障概率。由式（1）可知，求取故障概率的关键是计算λ0(t)、f1、f2，本文将进行详细介绍。

1.1.1 老化失效

输电线路任一元件发生故障均可导致线路停电，而元件因老化导致故障概率的变化情况可利用浴盆曲线进行描述[10]。威布尔分布通过设置不同的形状参数和尺度参数，可较好地体现浴盆曲线的不同阶段，其模型表达式为

式中，α、β分别为威布尔分布的形状参数和尺度参数。结合线路的故障历史数据，通过非线性最小二乘法对2个参数进行拟合。

1.1.2 运行工况

电力系统元件的传输功率超过某一定值时，由内部因素造成的故障概率会随着传输功率的增大呈现线性上升的趋势[11]。设PN为线路的额定传输功率，Plim为线路的极限传输功率，当线路长期运行在额定传输功率的约束内时，其故障概率为定值v0；随着传输功率的上升，线路的运行温度增高，故障概率上升。因此，定义Pt为线路年平均运行负荷，基于在量化长期运行工况下线路的故障概率f1可表示为

1.1.3 微气象预警

考虑到小样本情况下模型的有效性，基于关联规则理论[12]挖掘微气象告警等级与线路故障的关系，第j个微气象所属的第k个告警等级对输电线路发生故障的支持度S(Uj,k→V)可表示为

式中：σ(Uj,k→V)为事后确认第j个微气象特征因子在第k个告警等级下造成输电线路故障的次数；Ω为事务总集数量。

第j个微气象第k个告警等级与输电线路发生故障的置信度C(Uj,k→V)可表示为

式中，σ(Uj,k)为处于监测到第j个微气象在第k个告警等级下的总告警次数。

通过置信度可衡量微气象在不同告警等级下导致输电线路故障的可能性，当系统接收到多个微气象预警时，以预警值中最大置信度作为导致故障的附加概率f2。

1.2 故障后果评价

传统故障后果评价方法以线路故障后造成系统减供负荷为标准划分等级[6]，适用于配电网。考虑到输电网是闭环运行，某一回线路造成整个系统负荷的损失难以准确估计，对此从输电线路年平均运行负荷出发，将其与系统总负荷的比值作为衡量故障后果的评价标准，具有更为直观且易于统计的优势。参考文献[6]，将故障后果划分为5个等级，见表1。

表1 输电线路故障后果评分Tab.1 Evaluation of transmission line fault consequence

1.3 巡检周期制定

1.3.1 基础巡检周期

当仅考虑线路的老化失效和运行工况对故障概率的影响时，式（1）退化为

式中，γ1为内部渐变性影响因素的权重系数。

基于风险评估理论计算线路长期运行风险R0为

式中，g为输电线路故障后果评分值。

基础巡检周期忽略微气象的影响，其利用年运行风险R0制定线路的基础巡检周期，此处参考《中国南方电网有限责任公司设备风险评估管理办法》，将风险评估值划分为4个等级，以调控巡检工作量，输电线路基础巡检周期见表2。

表2 输电线路基础巡检周期Tab.2 Basic inspection periods of transmission lines

1.3.2 附加巡检任务

当计及微气象预警时，线路的短期运行风险值变为

式中，γ2为外部突发性影响因素的权重系数。

若R1评定等级高于R0，此时并非直接增加额外巡检，而是需要考虑巡检的必要性、紧急性；当考虑线路故障隐患数目较多时，在微气象的作用下，故障隐患发展为故障事件的可能性就越高，此时应适时增加巡检次数以降低故障风险。因此，建立附加巡检任务判定逻辑如图1所示。

图1 附加巡检任务判定逻辑Fig.1 Determination logic in added inspection task

为了衡量线路排班工作的合理性，定义巡检密度系数ρ为

式中：T为线路的基础巡检周期；dw为线路的微气象预警日；dl为该线路上一次巡检日。

设dn为下一次巡检日，可知式（9）满足dl＜dw＜dn，ρ＞1，且随着dw越接近dn，ρ逐渐减小，当ρ≥4时，dw距离dl为1/4周期之内，此时不更新巡检周期可避免人力浪费；当ρ≤4/3时，dw距离dn为1/4周期之内，可将下一次巡检日提前，即令dn=dw，优先巡检存在高故障风险的线路。

当考虑线路故障隐患数目较多时，在微气象的作用下，故障隐患发展为故障事件的可能性就越高，此时应适时增加巡检次数以降低故障风险。记线路在dw前经历了h次巡检，其剩余的累积故障隐患数为m(h)，依据文献[7]对累积故障隐患数与基础巡检周期T的关系进行建模，可得

式中：h为巡检次数；k为每次线路巡检可消除的故障隐患比例；μ为线路故障隐患出现的频次。

当不考虑微气象预警时，h次巡检后线路的累积故障数为

倘若线路在巡检年限内接收到多次微气象预警，一味采取巡检日提前的措施，则无法降低线路的累积故障数，可在dw时刻为线路增加1次额外巡检。经(h+1)次巡检后线路的累积故障数可表示为

此时，可通过比较h次巡检与(h+1)次巡检后线路的累积故障数来判断是否要增加额外巡检计划。n(h+1)/n(h)的比值越小，表明增加巡检次数所取得的收益越大、必要性越高，设定0.7为判断巡检次数增加必要性的阈值。

2 人机巡检计划优化模型

2.1 模型构建

巡检的目标是及时发现并处理潜在的缺陷和隐患，因此，模型中首要考虑的就是输电线路运行的可靠性，并通过合理的人机巡检任务分配可降低运维人员的巡线时间及成本，即

式中：Z1为故障风险成本，104¥；Z2为巡线经济成本，104¥。

1）故障风险成本

式中：η为单位电价，104¥/（MW·h）；pi(t,f1,f2)为线路i的故障概率；L为系统下一年计划巡检的线路数量；Pi为线路i的运行平均功率，MW；τ为线路的等值停运时间，包括故障时间和修复时间，h；xi为决策变量，xi=0表示线路i的巡检方式为人工巡检，xi=1为无人机巡检；ξ、ψ分别为线路在每次经历人工巡检和无人机巡检后故障概率的回退因子，可依据累积故障数n(h)进行设定，且满足ψ＜ξ；hi为线路i的计划巡检次数，包括基础巡检周期和附加巡检任务。

2）巡线经济成本

式中：ε为单位工时成本，包括运维人员工资、工伤费用、培训费用等，104¥/h；π为无人机每次执行任务的平均成本，包括无人机等值折旧费用、维护费用等，次/104¥；si为线路i的巡检长度，km，实际巡检任务的分配往往是以杆塔编号的形式进行给定，例如，以某线路30#杆塔为巡检起点，40#杆塔为巡检终点，假定杆塔间的平均档距为500 m，那么巡检长度约为0.5×（40-30）=5 km；ω为单位时间人工巡检距离，km/h；φ为单位时间无人机巡检距离，km/h，而无人机巡检效率约为人工巡检的10～15倍[5]，故设定φ=10ω；Mi为线路i的巡检方式与其所处微地形的匹配程度。

《超高压输电公司二〇二〇年设备运行维护策略》指出，微地形区段包括防雷区、防风防汛区等，对无人机具有较强的偏好性，采用人工巡检的形式难度大，耗时长。此外，交叉跨越区必须采用无人机进行巡检，属于特殊区段。因此，设计微地形匹配度M对巡检方式的偏好程度进行赋值，本文为输电线路所处一般区段、微地形区段和特殊区段的M分别赋值为1、5、10。

2.2 模型求解

考虑所建模型的决策变量为离散变量，可选用启发式算法进行求解。遗传算法GA（genetic algorithm）[13]是一种经典的智能优化算法，目前，已在电力系统诸多领域得到应用。模型将GA中连续变量的种群编码为二进制的形式，0表示采用人工巡检，1表示采用无人机巡检。基于GA对人机优化模型进行求解。

3 算例分析

3.1 数据收集

收集到某电网负责管理的26回500 kV线路。26回线路的统计故障次数总和为143次，其中，与气象相关（如雷击、风偏）的有125次，说明线路故障与外部气象因素有显著的关联。由于部分现场数据资料的缺乏，巡检周期的计算并非以线路全长进行统计，而是以实际发生过故障的线路区段作为验证对象；同时，年均运行负荷以与额定值的比例估算给出，并作为f1的计算参数。

3.2 动态巡检周期计算

3.2.1 基础巡检周期

（1）统计线路投运时间与故障事件发生时间差值相同的故障事件数，即线路投运后逐年发生故障的次数总和，当故障时间与投运时间为同一年时，记线路服役年限为1 a，故障时间与投运时间差值最大为26 a，统计结果见表3。

表3 输电线路历史故障时间统计Tab.3 Statistics of transmission line history fault time

（2）计算故障事件随服役年限的累积概率密度分布，并利用非线性最小二次法对威布尔参数进行估计。图2给出了参数拟合结果，其标准差为0.049 6，由此可得α=10.577 2、β=1.543 9，将其代入式（2）即可得到老化失效模型，β＞1为损耗失效期，其对应故障概率逐年升高的元件寿命末期，而样本线路服役年限最短已有13 a，验证了方法的合理性。

图2 参数拟合结果Fig.2 Parameter fitting result

（3）取v0=0.05、Plim=1.4PN、γ1=0.5，利用式（7）与故障后果评分计算线路运行风险值。以500 kV玉砚乙线为例，其投运时间为2006年，已服役16 a，将t=16代入式（2）得λ0(16)=0.182 8；因PN＜1.1PN＜1.4PN，故运行工况影响因子为f1=0.287 5；将g=800代入式（7）得R0=168.848 0。由表2可知，其风险评级为Ⅲ级，处于较高风险，故推荐的巡检周期为60 d。

通过上述计算可得26回线路的基础巡检周期表。为方便后文附加巡检任务的安排，在制定基础巡检周期后，以1月1日作为巡检执行时间起点，依次对26回线路进行巡检的初始执行时刻统计。

3.2.2 附加巡检任务

2012年4月5日，强对流天气袭击500 kV桂山乙线，所在区段出现雷雨、大风和冰雹等罕见微气象，大风造成122#塔A相导线单联某串绝缘子内串从碗头挂板处脱落，导致该线路发生风偏故障。假定在4月5日前系统收到了线路所在区段的微气象雷电黄色预警、暴雨预警、风力红色预警和覆冰黄色预警，由式（4）、（5）计算可得f2={0.42，0.04，0.69，0.34}，取最大值f2=0.69。

考虑在灾害天气作用下，输电线路的故障概率相较于正常天气而言呈现较为显著的风险突增现象[14]，故取γ2=1，由式（8）得R1=278.012 1，故其风险等级为Ⅳ级，而R0=139.450 3，风险处于Ⅲ级。此时需计算巡检密度系数，在4月5日之前，桂山乙线在巡检年份的巡检起始时刻依次为1月11日、3月11日，不考虑微气象预警，则下一次巡检时刻在5月11日，代入式（9）得ρ=3。由于 4/3＜ρ＜4，说明预警日距离前后两次巡检时间均较为长远，此时需进一步判断是否需要额外巡检。设k=0.99、μ=10，依据式（10）～（12）计算2次巡检后线路剩余的故障隐患数m(2)=6.06、累积故障数n(2)=1.056 3、3次巡检后累积故障数n(2+1)=0.716 1，由于n(2+1)/n(2)=0.677 9＜ 0.7，说明增加巡检次数所取得的收益较大，可在接收到微气象预警后增加1次巡检。若能在4月5日之前，通过巡检发现导线存在的故障隐患，则可能避免故障事件的发生。

以上是以一个实例分析完成了基础巡检周期和附加巡检任务的计算流程，后续可通过同样的手段对其他线路进行计算。

3.3 人机巡检优化

3.3.1 模型参数

人机巡检模型中Z1及Z2的计算涉及参数见表4，Pi以额定功率与年均运行负荷的乘积给定，并设定线路额定功率为1 200 MW。此外，GA的种群大小设定为150、遗传代数为50、交叉概率为0.9，并利用MATLAB R2019a软件对所提方法进行编程。

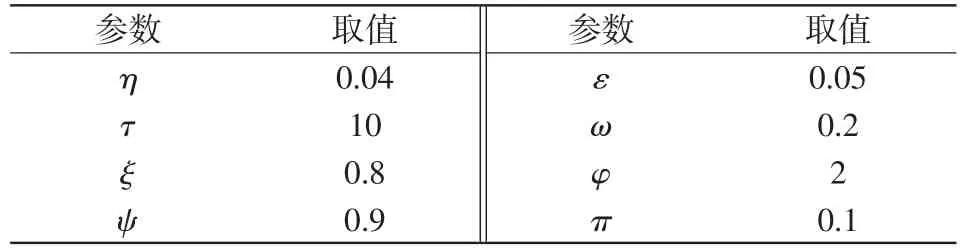
表4 人机巡检模型参数Tab.4 Parameters of human-machine inspection model

3.3.2 方案对比

设计5个方案以验证所提方法的有效性。

方案1巡检计划基于基础巡检周期制定，所有任务采用人工巡检的形式。

方案2巡检计划基于基础巡检周期制定，所有任务采用无人机巡检的形式。

方案3建立人机巡检优化模型，模型中不考虑微地形匹配度，巡检计划基于基础巡检周期，利用GA进行优化求解。

方案4建立人机巡检优化模型，模型中考虑微地形匹配度，巡检计划基于基础巡检周期，利用GA进行优化求解。

方案5建立人机巡检优化模型，模型中考虑微地形匹配度，并假定每回线路在巡检年度会接收到4次预警，以此计算动态巡检周期，利用GA进行优化求解。

各方案优化对比见表5。

表5 方案优化结果对比Tab.5 Comparison of optimization result among schemes

1）对比方案1、方案2、方案3

故障风险成本：方案1故障风险成本最低，约为方案2的42%，这符合人工对故障隐患识别率高于无人机的设定，方案3成本处于两者中间。

巡线经济成本：方案1最高，方案3次之，方案2最低，这是因为方案1的巡检工期最长，而巡线经济成本中涵盖了单位工时成本。

总成本：方案3总成本最低，方案1、2次之。

巡检工期：其排序与巡线经济成本一致，方案1的巡检工期为方案2的10倍，这是由于模型中定义无人机巡检效率为人工巡检的10倍，方案3的巡检工期对比方案1降低了近3 000 h。

综上，经过构建模型进行人机巡检方式优化后，方案3获得了最高的总效益，说明对人工巡检方式进行优化求解是合理且必要的，但超过6 000 h的巡检工期仍较长，当运维人员面临因微气象而突增电力巡检压力时，较长的工期可能导致任务不能及时完成。

2）对比方案3、方案4

故障风险成本：方案3优于方案4，当在模型中考虑微气象匹配度时，更多线路被推荐通过无人机进行巡检，故提高了方案4的故障风险成本；且方案4中类型为微地形区段或特殊区段的线路大多被推荐采用无人机的形式进行巡检，这符合工程实际。

巡线经济成本：方案4优于方案3。

总成本：方案4比方案3的高约100×104¥。

巡检工期：方案4的巡检工期约为方案3的60%，方案4的巡检工期指标显著优于方案3。

综上，在模型中计及微地形匹配度后，虽故障风险成本及总成本有一定升高，但显著降低了巡检工期，当需对更多线路进行巡检时，通过在模型中添加微地形匹配度可带来更符合工程实际的安排。

3）对比方案4、方案5

故障风险成本：方案5显著优于方案4，其故障风险成本降低超过150×104¥。

巡线经济成本：方案4略优于方案5，考虑微气象后巡检任务增加，提高了巡线经济成本。

总成本：方案5优于方案4。

巡检工期：方案5巡检工期相较于方案4有所增加，但在可接受的范围内。

综上，模型中计及微气象预警后，虽巡线经济成本及巡检工期有一定升高，但显著降低了巡检的总成本，所提方法取得了效益和工期的折中。

4）对比5个方案

结果表明：模型方案5的总成本在5个方案中为最低值，相较于总成本最高的方案2降低约23%；而巡检工期相较于故障风险成本最低的方案1降低约54%，验证了所提方法的有效性。通过人机巡检模型优化、微地形匹配度构建和考虑微气象预警的动态巡检周期3个要素的共同考量，可保证巡检计划在具有高综合效益下，降低线路故障风险，提高输电系统运行可靠性。

4 结论

（1）基于线路老化失效、运行工况和故障后果多要素计算线路风险，并依据风险制定差异化巡检周期，可降低巡检的工作量，避免因巡检过量而浪费人力；

（2）结合微气象预警所带来风险附加值，通过计算线路巡检密度系数和累积故障隐患数以判定是否进行提前、额外巡检，使巡检周期可依据外部气象条件进行动态调整，方法简单有效，易于工程应用；

（3）以人机巡检计划作为研究场景，优化结果表明，微地形匹配度可降低线路巡检工期，考虑微气象预警对巡检计划进行动态安排后，虽巡线成本有所提高，但故障风险下降显著，提升了巡检计划的总效益，保障了线路运行的可靠性。