NPC型三电平并网逆变器自适应模型预测控制

刘春喜，田宝奇，刘志乐，赵昱诚，张天琦

（辽宁工程技术大学电气与控制工程学院，葫芦岛 125105）

近年来，随着新能源发电技术的大力发展，并网逆变器成为新能源发电系统中的关键设备[1]。与两电平逆变器相比，二极管中点箝位NPC（neutral point clamped）型三电平逆变器具有更大的带宽和更高的电压范围，能够有效改善波形质量，因此，它在高电压等级的工业领域得到了广泛应用[2]。有限控制集模型预测电流控制FCS-MPCC（finite control set model predictive current control）具有快速瞬态响应、易于实现、灵活可控等特点，因此成为并网逆变器的一种常见控制方法。然而由于模型预测依赖于模型参数，当模型参数出现误差时，会使得系统的控制精度降低[3-8]，动态响应性能变差[9]。另外，由于三电平逆变器开关矢量多，导致处理器运算量增加，加重了系统的计算负担[10-12]。

针对模型参数误差对系统控制精度的影响，文献[3]针对两电平逆变器，基于无差拍电流控制方案通过简化系统模型来缓解控制器的参数敏感性问题，消除了模型误差对系统的影响；文献[4]采用双闭环控制系统对电网侧的阻抗敏感度进行分析，提出了一种适用于不同的控制系统的自适应控制策略；文献[5]在三电平PWM整流器的基础上引入了多模型反馈校正环节，通过设计自适应控制器在线辨识系统预测模型，解决了因参数误差导致的电流畸变问题；文献[6]通过优化求解线性矩阵不等式问题，利用全状态观测器来消除模型误差对系统的影响；文献[7]设计了一种基于输出电压的二阶自抗扰控制方法，用来提高控制系统的扰动观测能力；文献[8]对于两电平逆变器求解系统预测和实测状态下误差的最小值来更新系统的数学模型，提高了系统在参数扰动情况下模型预测的准确度，消除了参数突变对系统的干扰。上述文献从多个方面对减小模型参数误差进行了研究，但涉及NPC型三电平并网逆变器拓扑的研究并不多。针对三电平并网逆变器采用FCS-MPCC造成计算量大的问题，文献[10]利用系统模型方程预测出最优控制向量，通过减小最优向量与可用向量之间的距离来选择逆变器输出向量，减小了计算次数；文献[11]根据逆变器电压矢量与参考矢量的距离，选择最优矢量参与预测模型的遍历寻优和价值函数的计算，达到减小计算量的目的，但上述两种方法均没有考虑计算延时对系统的影响；文献[12]利用单目标代价函数简化寻优步骤方法，通过选择冗余小矢量减小预测次数，从而提高了寻优效率，但这种方法的预测精度低。

为降低参数扰动的影响，减小系统计算量，该文研究了一种改进的NPC型三电平并网逆变器自适应模型预测电流控制A-FCS-MPCC（adaptive finite control set model predictive current control）策略，给出了方案设计和开关序列优化方法，并基于Lyapunov判据分析了系统稳定性，最后通过时域模型仿真进行了验证。

1 NPC型三电平并网逆变器FCS-MPCC

图1为NPC型三电平并网逆变器拓扑，图中，Udc为直流侧电源电压，Cdc1、Cdc2为直流侧稳压电容，Da1、Da2为a相的钳位二极管，Sa1～4、Sb1～4、Sc1～4分别为三相的开关管，L为并网侧滤波电感，R为并网侧线路电阻，ea、eb、ec为三相电网电压，M、N分别为直流侧和并网侧电压中性点，ia、ib、ic分别为三相的并网电流。

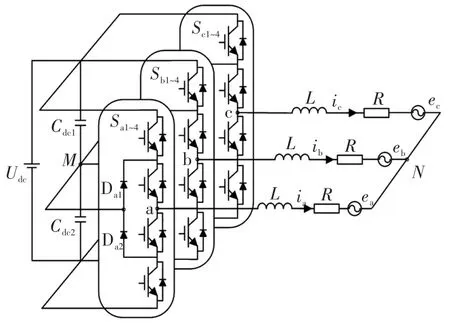
图1 NPC型三电平并网逆变器拓扑Fig.1 Topology of NPC-type three-level grid-connected inverter

当三相电网平衡时，根据基尔霍夫定律并进行Clark/Park变换，建立逆变器的数学模型为

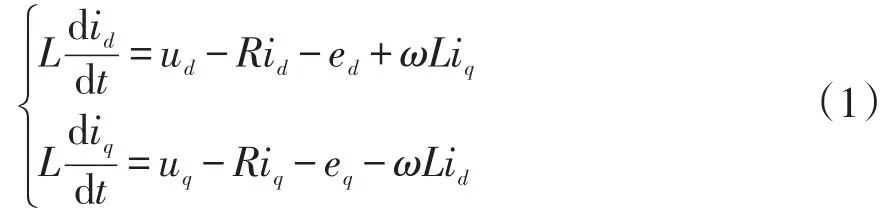
式中：，id、iq为dq坐标系下的并网电流；ud、uq为dq坐标系下的输出电压；ed、eq为dq坐标系下的并网电压；ω为角频率。

NPC型三电平并网逆变器根据三相桥臂的不同状态可以产生27种开关组合，19种不同的电压矢量，其基本电压矢量分布见图2。

图2 NPC型三电平并网逆变器基本电压矢量分布Fig.2 Distribution of basic voltage vectors of NPC-type three-level grid-connected inverter

对式（1）进行离散化，可得到基于dq坐标系下交流侧三相电流的离散数学模型为

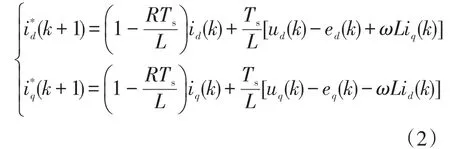
式中：id(k)、iq(k)、ud(k)、uq(k)和ed(k)、eq(k)分别为第k个采样周期的并网电流、输出电压和并网电压；为第(k+1)个采样周期的并网电流；Ts为采样频率。

由于三电平并网逆变器直流侧中点电位波动会对逆变器的输出波形产生影响[12]，需要对直流侧中点电位平衡进行控制。因此，根据逆变器的开关状态分别对电容电压进行预测，预测电压为

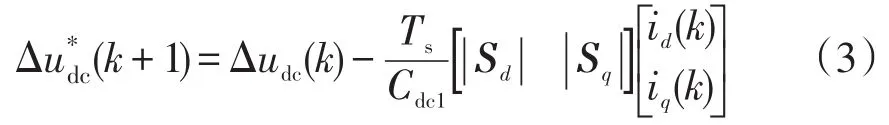
式中：Δudc=udc1-udc2，udc1和udc2为直流侧稳压电容Cdc1和Cdc2的电压；Sd和Sq为电压矢量在dq坐标系下的分量。

在NPC型三电平并网逆变器的价值函数中，除了考虑传统的dq轴跟踪电流外，还需考虑中点电位平衡问题。为此，可将价值函数设计为

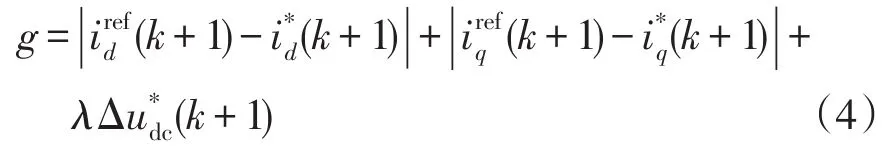
式中：上角标ref表示电流的参考值；λ为直流侧中点电压平衡的权重系数，可通过试凑法得到[13]。FCS-MPCC策略是选择最佳开关状态，在每个周期针对不同的开关组合状态执行27次计算，得出最佳成本函数。

2 NPC型三电平并网逆变器A-FCS-MPCC

2.1 方案设计

考虑系统模型式（2）的参数受外部干扰，实际的网侧阻抗动态模型可以表示为

式中：x=1-TsR/L；y=Ts/L；U(k-1)=u(k-1)-u*(k-1)，u*(k-1)为预测的电压扰动矢量。在实际控制系统中，参数x和y都是未知的，需要通过参数估计器对他们进行实时调整。

根据式（5）构造出参数估计器的第k时刻预测电流为

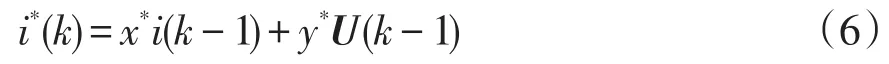
式中，x*和y*分别为估计器参数。其收敛性可以通过使用电流预测误差参数自适应来实现，即

电流误差主要由参数扰动引起，可作为中间变量去调整估计器参数，使电流误差达到最小。采用迭代梯度法将d轴电流表示为

式中：D(k-1)=[id(k-1),Ud(k-1)]T,τ(k)=[x(k),y(k)]T；Ud(k-1)为第(k-1)时刻d轴电压向量；x(k)和y(k)为第k时刻参数动态模型。

参数估计器的收敛性可以通过使用估计误差进行适当的参数调整来实现，将参数误差定义为

预测向量τ*(k+1)可通过τ*(k)递归表示为

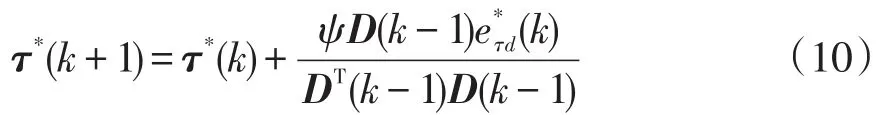
式中：ψ为自适应还原因子；为d轴的参数预测误差；τ*(k)为第k时刻预测的系统参数。

电压扰动导致电流的预测过程表现为非线性，在此采用一种自适应观测器结构来解决该问题。因为预测的参数矢量收敛于实际的参数矢量，即τ(k)=τ*(k)，所以可构造出自适应观测器，即

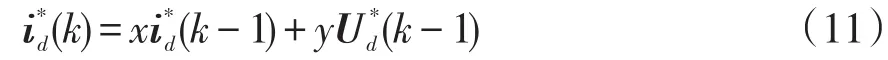
为了保证收敛性，定义离散型二次误差函数为

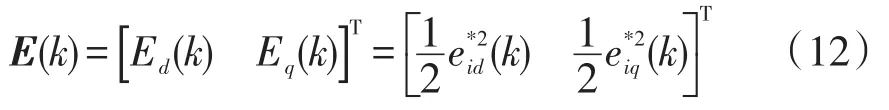
式中：Ed(k)和Eq(k)分别为dq坐标系下的误差函数；和分别为dq坐标系下的电流预测误差。在预测测量误差中，采用共轭梯度法使误差函数E(k)最小化，误差函数为

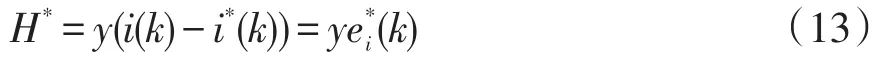
根据式（13）估计扰动电压，电压预测量等效为

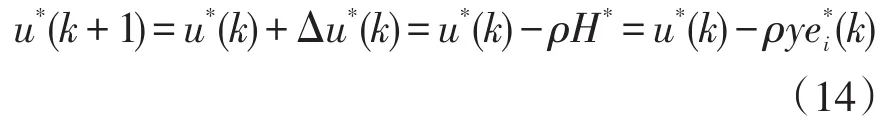
式中：u*(k)=e(k)-ωLi(k)；Δu*(k)为预测电压变化量；ρ为自适应增益。将预测的u*反馈到式（5）中，用来消除电压干扰。因此，参数预测量τ*可以用于式（11）自适应观测器参数的自适应调优。即使在参数变化的情况下，也能准确地观测到扰动电压向量。根据式（10）和式（14）的递归函数，电压扰动量和参数扰动量将会收敛到它们的实际值。

输出电压可用电流参考值及电压预测量进行估计，表达式为

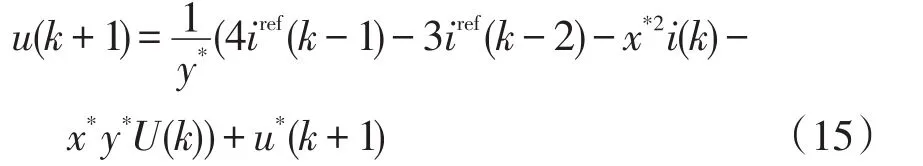
式（15）也可以用于提取并网逆变器的交流线路电压。

2.2 直流侧中点电位平衡分析

由于NPC型逆变器拓扑结构比较特殊，在控制系统中，直流侧的两个电容在一个采样周期内的充放电情况并不均匀，在直流中性点会产生中点电位差，影响系统的稳定运行。

为了可以更好地平衡中点电压，在不影响系统稳定性的情况下，使得中点电位差尽可能小。根据式（4），将价值函数改写为

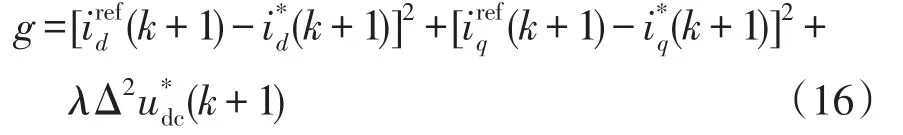
式中，λ的取值范围与所控制变量在价值函数中的优先级有关，前两项分别为(k+1)时刻dq坐标系下电流参考值与电流预测值之间误差的平方，后一项为(k+1)时刻直流侧两电容中点电位差的平方。

2.3 开关序列优化

在NPC型三电平并网逆变器中，逆变器中性点M与网侧中性点N之间的输出电压可以表示为

式中，Sa、Sb和Sc为逆变器各相的开关状态。根据式（17），NPC型三电平逆变器中点输出电压幅值可在27种工作状态下获得，具体数值见表1。

表1 开关状态与输出电压Tab.1 Switching status and output voltage

由于预测过程的每个步骤中需要计算27次，存在较大的计算量。根据表1中的数值，将UMN限制在±Udc/6范围内[14]，使遍历的开关组合减少到19次，从而降低了系统的计算负担。图3显示了开关序列优化后的可用开关组合。

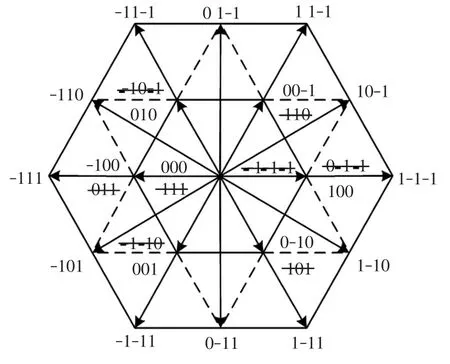
图3 开关序列优化后的可用开关组合Fig.3 Combination of available switches after the switch sequence is optimized

由于实际系统存在采样和控制延时，影响系统的控制性能，因此采用两步预测法来补偿这部分延时。将式（2）和式（3）进行改写，在第k时刻预测第(k+1)时刻的电流，并以该值为起点再进行一次预测，得到第(k+2)时刻的并网电流和中点电压预测模型，即

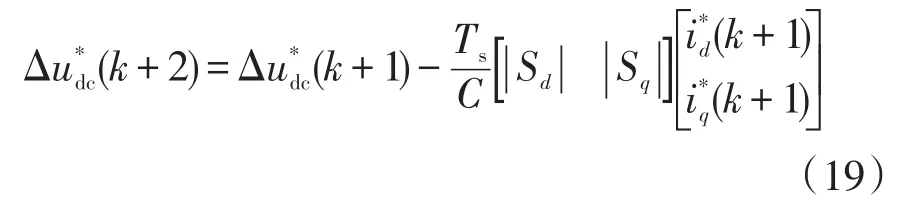
针对补偿后的预测电流和中点电位对价值函数进行重新评估，可得

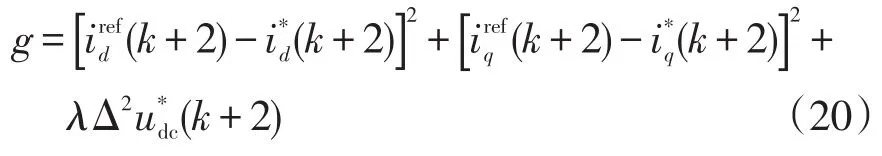
式中：前两项分别为(k+2)时刻dq坐标系下电流参考值与电流预测值之间误差的平方，后一项为(k+2)时刻直流侧两电容中点电位差的平方。当采样周期足够小时，可以近似认为第k时刻电网参考电流等于第(k+2)时刻电网参考电流。

将上述优化算法加入到NPC型三电平并网逆变器的控制过程中，得到A-FCS-MPCC策略结构，见图4。图中虚线框内分别标注了FCS-MPCC方法部分、自适应策略部分以及A-FCS-MPCC方法部分。

图4 A-FCS-MPCC策略结构Fig.4 Structure of A-FCS-MPCC strategy

3 系统的稳定性分析

将式（7）和式（9）的两个函数作为控制输入，设计一个基于系统误差的Lyapunov函数为

为了使式（21）收敛，其必须满足的条件为

由于电压扰动的连续性，采样频率远远大于带宽，根据式（11）和式（15）中的自适应规律，的变化量为

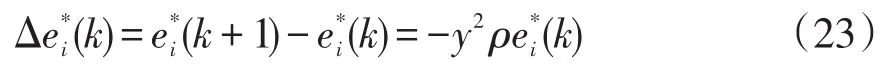
为满足式（24）的稳定性，自适应增益ρ的取值为0＜ρ＜(2/y2)。将式（23）代入到式（24）中，表示为

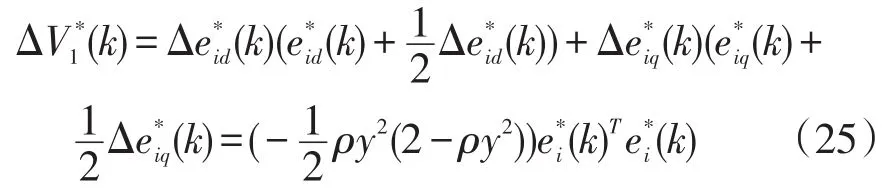
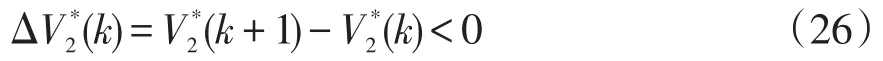
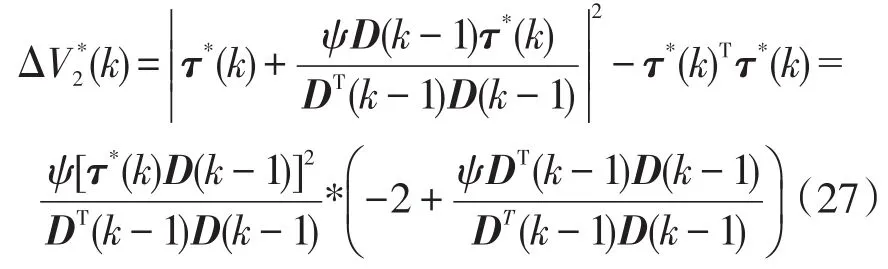
若ψ∈[0,2]，则式（27）中括号项为负，满足了收敛性和稳定性条件，即

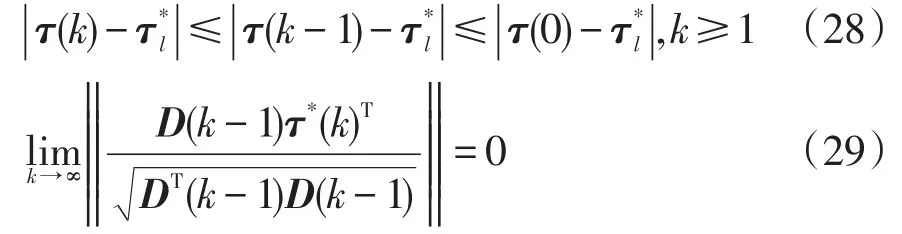
4 仿真验证与分析

为了验证A-FCS-MPCC算法的有效性，使用MATLAB/Simulink建立了A-FCS-MPCC的实例仿真模型，参数见表2。在无参数扰动情况下，将所提控制方法并网电流与比例积分-空间矢量脉宽调制PISVPWM（proportional integral-space vector pulse width modulation）方法和传统FCS-MPCC方法并网电流进行对比，分析三者的稳态性能、动态响应性能以及开关频率分布情况，表3给出了PI-SVPWM控制参数和A-FCS-MPCC控制参数。此外为验证参数突变导致的参数偏移适应性，将不同滤波电感的参数辨识情况与参考值进行了对比。

表2 并网逆变器参数Tab.2 Parameters of grid-connected inverter

表3 控制参数Tab.3 Control parameters

4.1 稳态响应性能对比

由于网侧等效电阻扰动对系统的影响较小[15]，因此以下仅分析滤波电感出现扰动的情形，将电感扰动范围控制在±50%。3种控制方法的三相并网电流波形见图5。从图5（a）中可以知，PI-SVPWM控制下的三相并网电流控制精度低，谐波含量大，总谐波失真THD（total harmonic distortion）值约为5.72%；从图5（b）中可知，传统FCS-MPCC控制下的三相并网电流波形得到明显改善，但由于系统存在延时影响，电流控制精度依然较低，THD值约为2.91%；从图5（c）中可知，在A-FCS-MPCC方法下的三相并网电流控制精度显著提高，谐波含量很小，THD值约为0.87%。图6为NPC型逆变器输出侧ab相间的输出电压波形。

图5 三种控制方法的并网电流Fig.5 Grid-connected current for three control methods

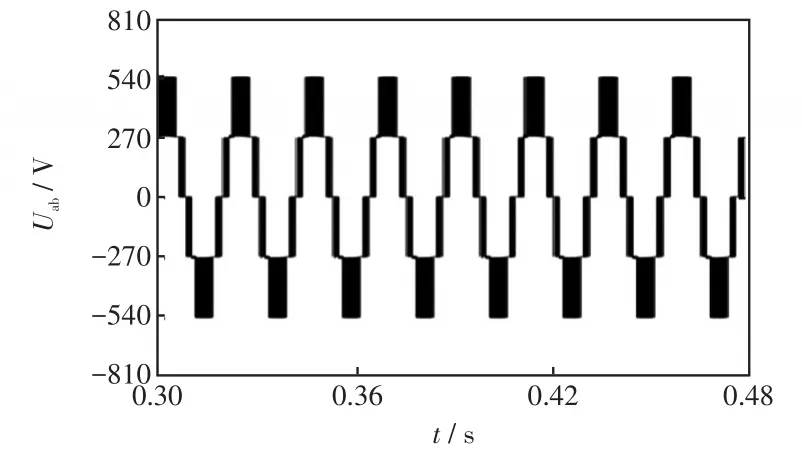
图6 输出电压波形Fig.6 Output voltage waveform

4.2 动态响应性能对比

在1 s时将参考电流从20 A突变为10 A，系统的动态响应波形见图7。图7（b）中，PI-SVPWM方法的电流跟踪时间为600 μs，跟踪速度慢且超调大；图7（d）中，传统FCS-MPCC方法的电流跟踪时间为380 μs，跟踪速度有所提高，但超调依然较大；图7（f）中，A-FCS-MPCC方法的电流跟踪时间仅用240 μs，响应速度更快，超调也更小。所以，A-FCSMPCC方法与PI-SVPWM和传统FCS-MPCC方法相比，具有更好的动态响应性能。

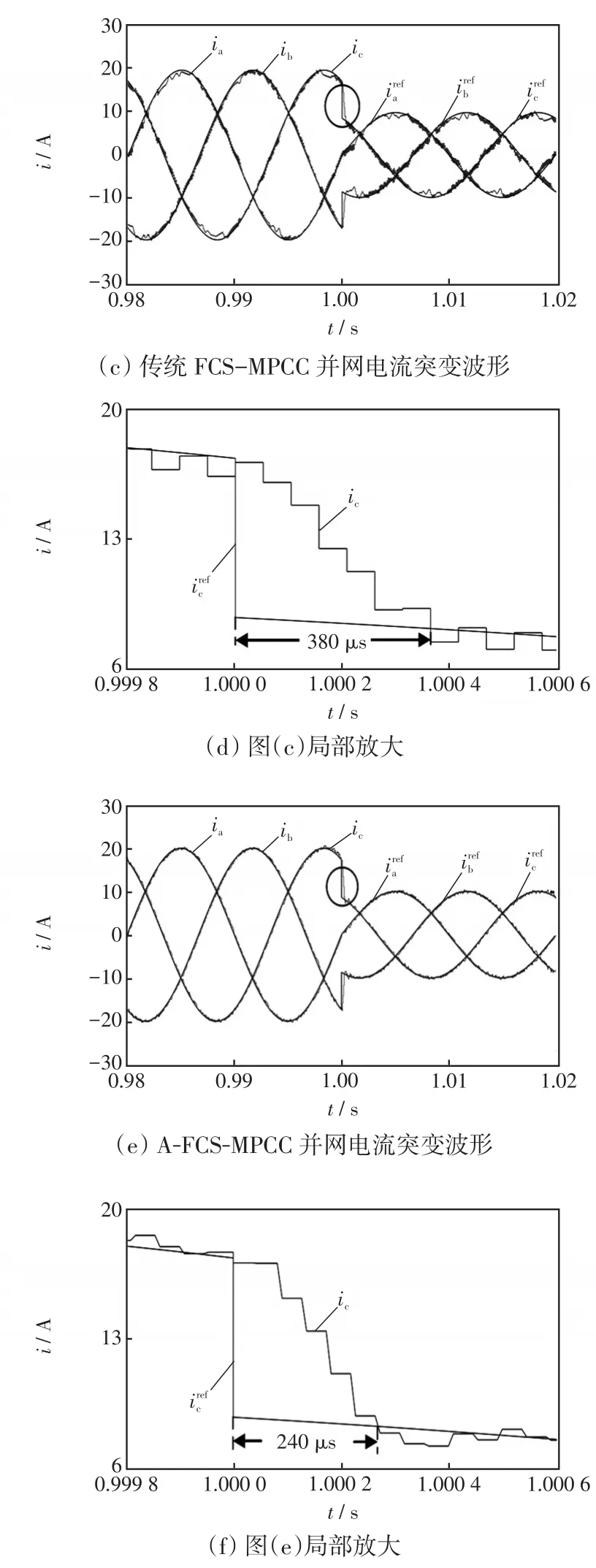
图7 三种控制方法的并网电流动态过程Fig.7 Dynamic process of grid-connected current for three control methods

4.3 开关次数对比

为了对NPC型三电平并网逆变器的开关次数进行定量的分析，在3.0～3.5 s时间内，通过3种控制方法对开关管Sa1的驱动脉冲进行说明，见图8。

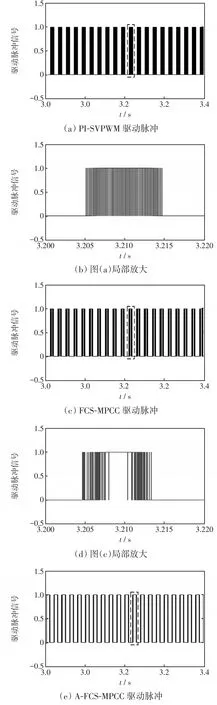
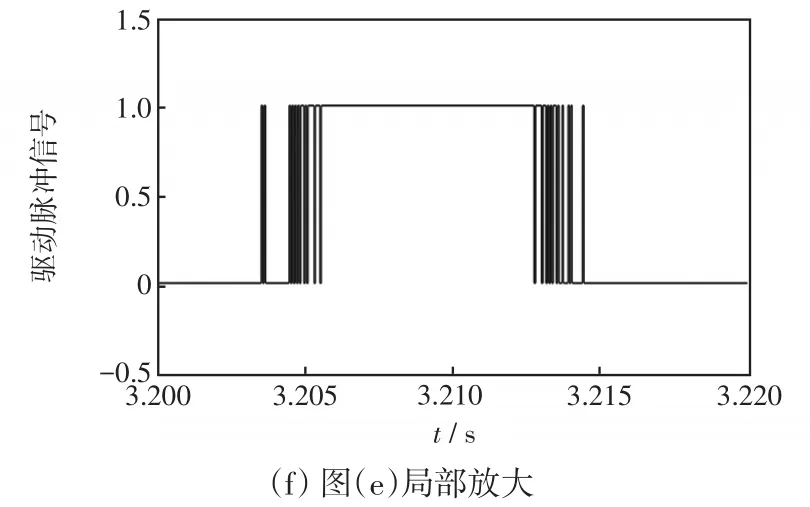
图8 三种控制方法的驱动脉冲Fig.8 Drive pulse for three control methods

PI-SVPWM方法的开关次数为3 021次，传统FCS-MPCC方法的开关次数为2 190次，而A-FCSMPCC方法的开关次数为1 834次，比前2种控制方法分别减少了39.3%和16.3%。

为了更加直观地表示3种方法的开关次数，图9给出了3种控制方法在优化与未优化开关序列情况下的开关次数对比，可见A-FCS-MPCC方法有效地减少了开关动作次数。

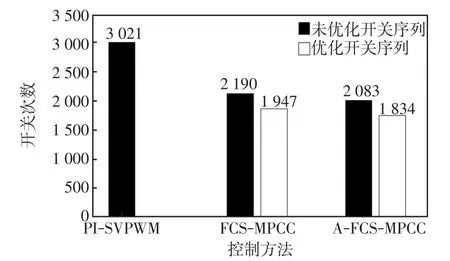
图9 开关次数对比Fig.9 Comparison of the number of switches

4.4 滤波电感估计

图10为滤波电感分别取5 mH、10 mH和15 mH时的参数估计曲线，可以看出参数估计辨识值十分接近参考值，验证了所提算法的准确性。

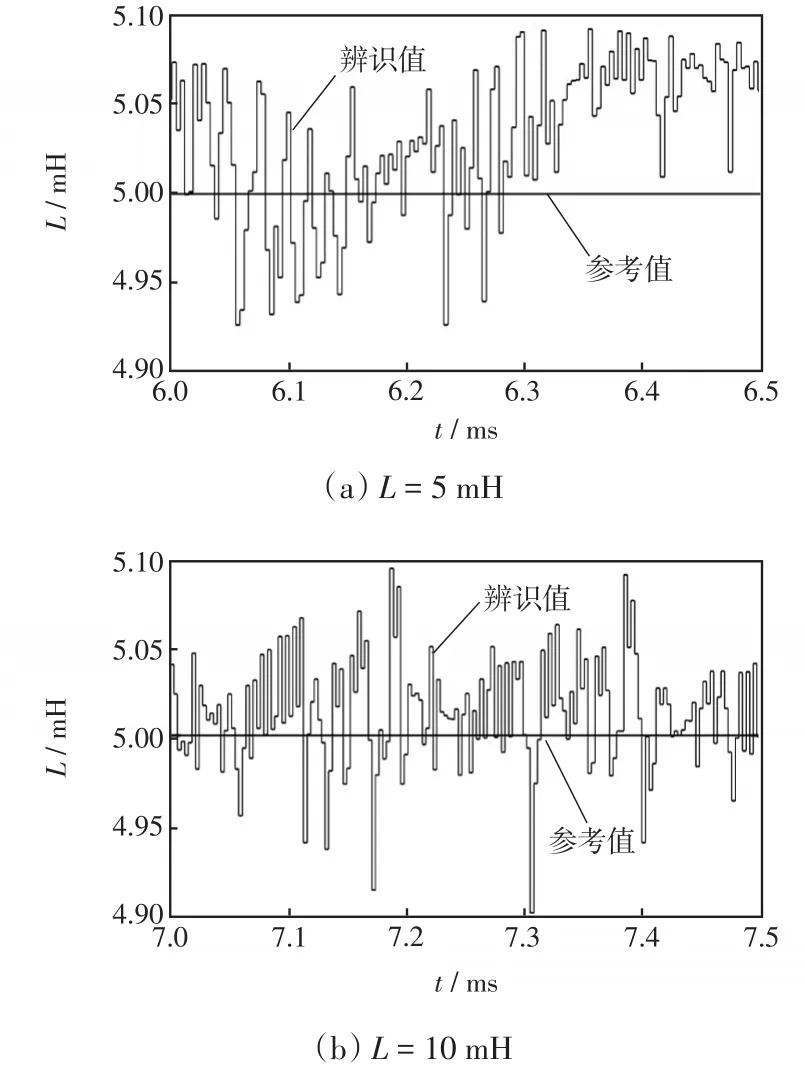
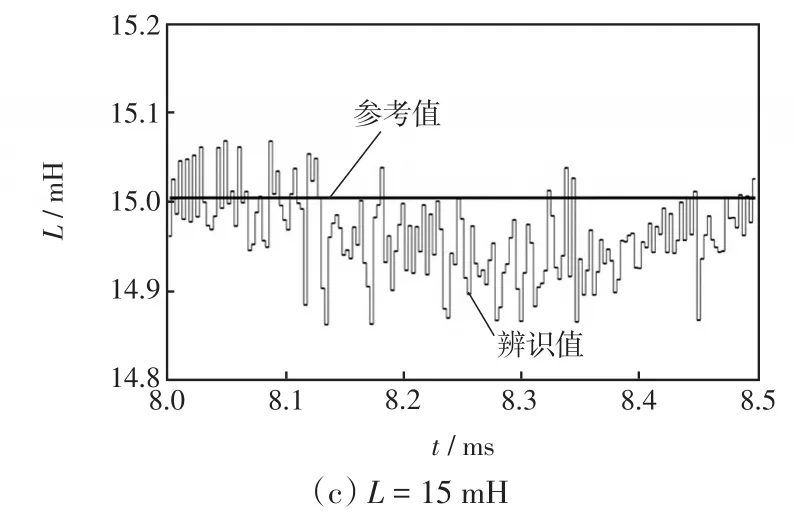
图10 滤波电感L估计曲线Fig.10 Estimation curves for filter inductor L

4.5 直流侧中点电位分析

为了验证所提算法的直流侧中点电位平衡能力，图11讨论了中点电位平衡权重系数λ分别为0.5和5.0两种状态下的直流侧电容电压的仿真结果。从图中可以看出，传统FCS-MPCC方法的中点电位平衡能力比较差，而A-FCS-MPCC方法有效提高了中点电位控制能力。

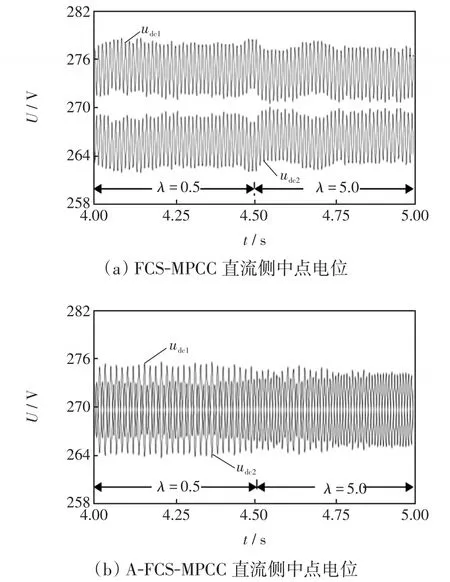
图11 直流侧中点电位波形Fig.11 DC-side midpoint potential waveform

5 结论

本文研究了一种改进的自适应模型预测控制策略，以解决负载参数扰动和系统计算量大的问题，通过仿真实例验证了A-FCS-MPCC算法的有效性，并得出以下结论。

（1）A-FCS-MPCC方法具有良好的动态响应性能，响应时间与PI-SVPWM和传统FCS-MPCC方法相比，分别减少了60%和36.8%，超调也更小。

（2）A-FCS-MPCC方法具有更低的开关频率，开关次数与PI-SVPWM和传统FCS-MPCC方法相比，分别减少了39.3%和16.3%，在减小计算量的同时也减小了系统的开关损耗。

（3）A-FCS-MPCC方法具有更好的自适应能力和抗干扰能力，能够在线识别参数误差。