基于数据驱动的交直流混联电网阻尼调制策略

邱家威，杨德友，蔡国伟，王丽馨，段方维

（1.东北电力大学电气工程学院，吉林 132012；2.国网辽宁省电力有限公司电力科学研究院，沈阳 110000）

交直流电网混联是我国能源发展演变的新阶段，在满足电网远距离、大容量输电要求的同时，其运行的脆弱性和耦合特性也使系统的失稳风险增加。一方面，大量动态行为时间尺度较小的电力电子设备使电网的安全稳定运行变得脆弱；另一方面，直流的灵活可控性使交、直流间状态变量广域耦合，控制变量及约束条件相互影响，导致系统动力学特性发生根本变化[1-5]。

现有对直流动态行为分析的研究大多基于直流运行特性和约束条件进行数学建模，通过线性化处理降低特征矩阵的阶数，来突出直流控制和运行特性对混联系统的影响，但不能有效解决交、直流耦合的非线性化问题[6-8]。

对于交直流混联系统，研究联络线功率对其小干扰稳定特性的影响时，不仅要考虑联络线断面总的输电功率，还要考虑并联交、直流联络线之间的功率配比[9-11]。文献[12]通过计算交直流混联系统区域间可用输电能力衡量系统的动态稳定性；文献[13]研究交直流混联系统连锁故障下交直流容量的最优配比，分析了直流故障概率和切机组合等因素对交直流容量最优分配的影响；文献[14]研究电网不同位置的直流故障对弱交流联络线功率波动的影响；文献[15]运用直流功率转移影响因子研究了单极闭锁故障下大直流功率转移对系统暂态安全稳定的影响。

基于发电机有功再调度的调制策略可通过下调联络线有功提高交直流混联电网区间弱阻尼模式的阻尼水平。文献[16]通过计算安全距离灵敏度，确定对关键断面影响显著的敏感机组和直流线路，制定相应的优化调度策略。参与有功再调度过程的敏感机组可依据阻尼比灵敏度大小加以筛选，当前主要通过计算特征值灵敏度实现。文献[17]基于含传递函数系统状态方程，提出振荡模式对传递函数灵敏度的解析表达式，但在实际运用中该方法求解复杂、耗时；文献[18]推导了特征值对控制参数灵敏度的解析表达式以实现控制参数的调节，但难以应对复杂系统的高阶次、非线性问题，灵敏度计算的准确性往往依赖数学模型的准确度；文献[19-20]基于广域测量数据利用摄动法计算灵敏度的方法规避数学建模求特征值的过程，计算过程简单、耗时短，但由于有功输出和辨识结果的实时波动，其计算结果往往随机性较大、准确度不高。为此本文提出定点滑窗摄动法计算发电机阻尼比-有功灵敏度以提高阻尼调制策略过程中灵敏度计算结果的准确度。

本文以随机负荷激励下系统的随机响应为数据集，运用随机子空间辨识法SSI（stochastic subspace identification）算法识别交直流混联系统潜在的弱阻尼模式。研究了直流输电容量占比对混联电网区间振荡阻尼比的影响，并深入研究两极直流系统发生单极闭锁后对交直流混联电网阻尼特性的影响，提出基于随机数据的定点滑窗摄动法计算发电机阻尼比-有功灵敏度，依据发电机有功再调度策略，实现故障后混联系统区间振荡阻尼的定向提高。

1 数据驱动的模态参数辨识

电力系统中时刻存在着由负荷随机波动等扰动所激发的随机响应，基于相量测量单元PMU（phasor measurement unit）实时提取的系统随机响应蕴含着能够反应系统振荡状况的动态特征信息，通过有效的随机数据辨识方法可以准确提取系统的小干扰特征信息。基于数据驱动的特征分析法利用含有系统动态特征的随机响应构造虚拟状态矩阵，通过矩阵特征分析辨识出系统的振荡频率、阻尼比等模态参数。其中，SSI算法以定阶简单、计算效率高、储存空间小等优势得到广泛、成熟的应用，并通过不断滑动数据窗可以辨识时变系统的模态参数，以适应动态过程复杂数据处理量大的系统。

在实际电网中，基于PMU的量测数据在时间上是离散的，经采样后构造系统状态空间模型为

式中：xk为第k个数据采集窗口的状态变量，xk∈Rn；yk为第k个数据采集窗口的系统输出变量，yk∈Rm；wk∈Rn、vk∈Rm为假定高斯白噪声，其期望值均为零；Ad∈Rn×n为离散系统状态矩阵；C∈Rm×n为系统输出矩阵。

SSI算法基于量测数据构造Hankel矩阵后，主要通过矩阵LQ分解、下三角矩阵奇异值分解和计算延伸观测矩阵步骤得到系统的虚拟状态矩阵和观测矩阵[21]。

根据系统连续和离散的采样关系，可求得连续系统状态矩阵为

式中：Ac∈Rn×n为连续系统状态矩阵；Δt为采样时间。

通过对连续系统状态矩阵的特征值分解，可求得系统的特征值为

式中：Λ=diag(λi)∈Rn×n，λi为系统模态第i个特征值，i=1,2,…,n；ψ为右特征向量。

则可求得系统特定振荡模式下的振荡频率fi和阻尼比ξi为

式中，αi、βi分别为特征值λi的实部和虚部。

2 基于定点滑窗摄动法的阻尼比灵敏度计算

在分析电力系统小干扰稳定性时，可通过灵敏度计算来分析某一参数的输入变化对系统输出响应的影响程度。传统的阻尼比-发电机有功灵敏度计算主要依据特征分析法，其解析表达式为

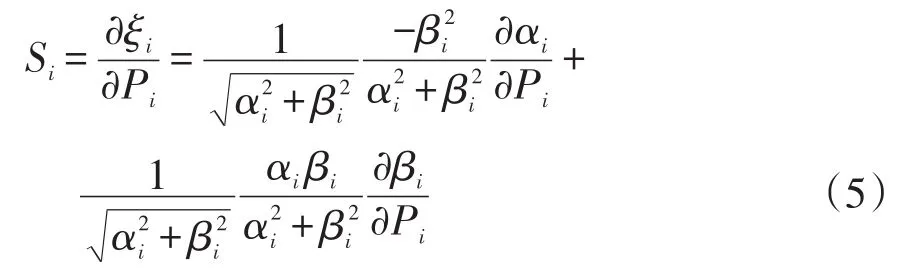
式中：Pi为发电机Gi的有功输出；Si为特定振荡模式下阻尼比对发电机Gi有功输出的灵敏度。

在实际电网的应用中，特征分析法求阻尼比灵敏度往往因系统状态方程的高阶次、非线性受制于特征值的求取，计算过程复杂、耗时，也不能很好地适应复杂系统拓扑结构及运行状态的变化，难以满足系统阻尼调制实时、快速性的要求。

将系统中发电机阻尼比-有功灵敏度定义为

式中：S为发电机对特定模式阻尼比的灵敏度；ΔP为发电机有功功率变化量；Δξ为特定振荡模式阻尼比的变化量。式（6）反映了发电机有功功率波动对特定模式阻尼比的影响。

在实际电力系统中，随机负荷扰动等自然扰动的激励下的发电机有功输出呈现小幅波动，图1为某发电机的随机响应时域数据。通过提取发电机侧PMU中有功自然摄动量作数据源，得到的阻尼比辨识结果也将小幅波动，基于二者可实现发电机阻尼比-有功灵敏度的递推计算。

图1 发电机有功随机响应Fig.1 Stochastic response of generator active power

但由于发电机有功差值和相邻窗口阻尼比辨识结果差值的波动，以摄动法计算的灵敏度均值往往不够准确，并且异常点出现频次较高。为了最大可能消除异常点，保证发电机有功变化对系统阻尼比影响程度的良好体现，本文提出基于定点滑窗摄动法的灵敏度计算方法。

由图1可知，发电机有功随机响应的数据值围绕在均值附近上下波动，具有相对固定的周期性，从宏观上看近似为图2所示关于纵轴对称和中心对称的周期图形。

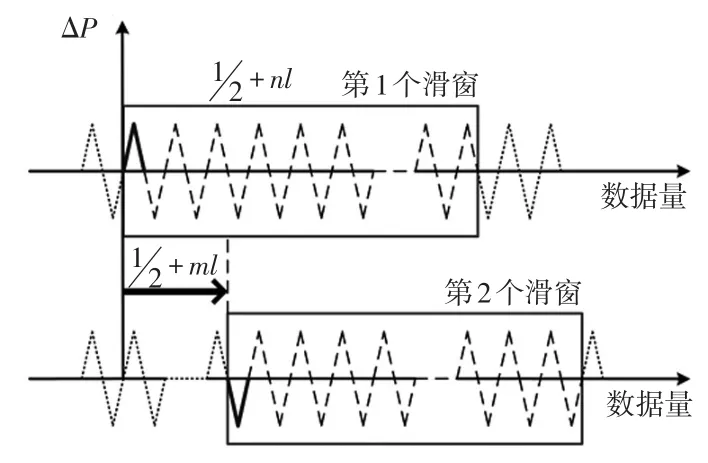
图2 定点滑窗摄动法求阻尼比灵敏度示意Fig.2 Schematic of damping ratio sensitivity obtained by fixed-point sliding window perturbation algorithm

通过对PMU量测数据的分析，可确定随机数据波动的周期数据长度l，窗口的起点位置为

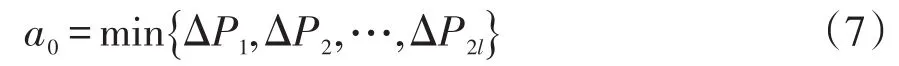
式中：a0为第一个窗口的起始数据；ΔPi为2个周期数据长度内第i个有功偏离平均值的差值，i=1,2,3,…,2l。

该窗口有功变化的平均值可表示为

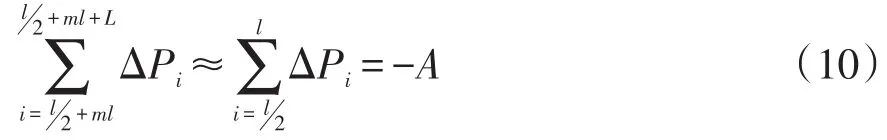
该窗口有功变化的平均值可表示为

则相邻窗口有功变化均值之差可表示为

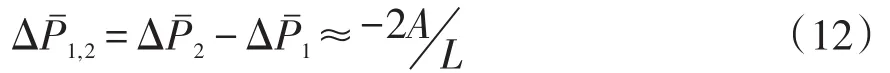
同理类推第k+1个窗口和第k个窗口之间有功变化均值的邻差 Δ,k+1为

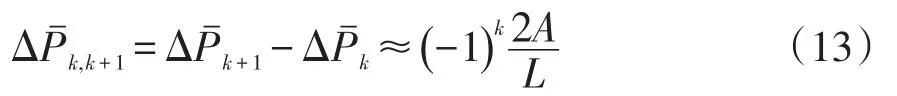
根据辨识结果可计算相邻窗口的阻尼比差值Δξk,k+1为

参考式（6）采用平均近似的方法可计算发电机Gj第k次滑动的阻尼比-有功灵敏度为

滑动计算N次，筛选过可求得发电机Gj的阻尼比-有功灵敏度均值为

依据定点滑窗摄动法可最大化有功变化均值的邻差，尽可能地消除滑窗过程中因有功邻差不规律变化带来的误差，保证发电机阻尼比-有功灵敏度的准确计算。

3 基于发电机有功再调度的阻尼调制方案

对于互联电力系统的区间弱阻尼模式，主要采用发电机有功再调度策略，通过送端发电机组下调有功输出，受端发电机上调有功输出，以降低交流联络线传输有功，达到提高区间模式阻尼比的目标。

（1）利用第2节提出的定点滑窗摄动法计算各发电机的阻尼比-有功灵敏度，依据灵敏度大小分别选取送、受端机组中可调度的灵敏度最大的发电机作为参与有功调制的发电机组合。

（2）根据送、受端发电机的运行状态和极限确定其最大可调度量，取二者中的最小值作为有功调制量ΔP，即

式中：PGs、PGr分别为送端和受端发电机有功输出；PGr,max、PGs,min分别为有功输出上限和下限值；ΔPGs、ΔPGr分别为送端和受端发电机的可调度量。

（3）在有功调制后重新监测混联系统阻尼水平，若不满足机电暂态小干扰稳定性要求，即阻尼比小于5%，则再次进行调制，交、直流混联电网阻尼调制流程如图3所示。具体步骤如下：

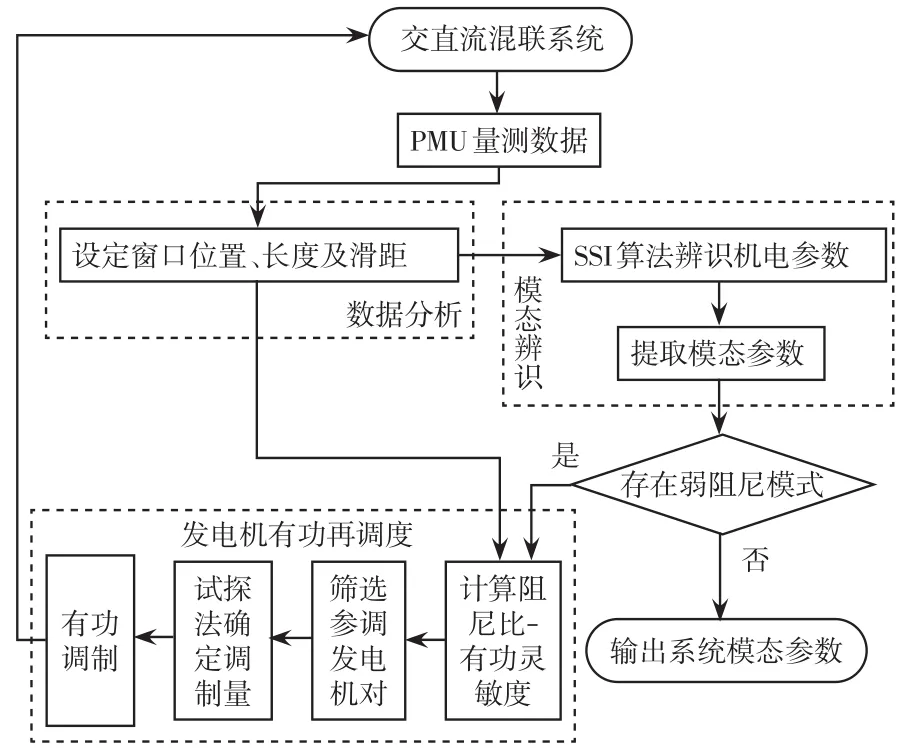
图3 交、直流混联电网阻尼调制流程Fig.3 Flow chart of damping modulation for AC/DC hybrid power grid

步骤1提取系统随机响应数据，设定滑窗信息，利用SSI算法辨识系统模态参数；

步骤2依据模态参数判断系统区间模式阻尼水平是否满足要求；

步骤3若存在区间弱阻尼模式，依据灵敏度计算结果，分别筛选出送、受端可调度的灵敏度最大的发电机，并由其运行状态和出力上、下限确定调度量；

步骤4进行发电机有功再调度，若区间模式阻尼水平仍不满足要求，则返回步骤1再次进行阻尼调制。

4 仿真分析

为了研究在混联系统联络线上交、直流配比和直流功率转移对区间振荡模式的影响，在改进的IEEE 4机2区交直流混联系统中仿真分析，并对SSI算法在混联系统中辨识的有效性加以验证。同时在16机5区交直流混联大系统中验证所提发电机阻尼比-有功灵敏度计算方法的可靠性和阻尼调制策略的可行性。

4.1 直流单极闭锁前、后模态辨识

在有功潮流分布方面，系统的区间振荡状况主要受联络线上输送有功功率及联络线断面交、直流的有功配比的影响。图4给出了在4机2区交、直流混联系统联络线总的有功功率不变时，同一时间断面下随直流输电功率的增加混联系统区间振荡的阻尼比和频率的变化曲线。

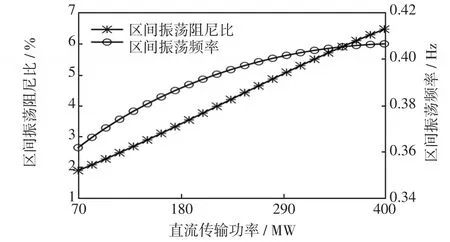
图4 区间阻尼比、频率随直流有功增加变化趋势Fig.4 Trends of interval oscillation damping ratio and frequency with increase in DC transmission active power

由图4可知，在混联系统交、直流联络线并联运行情况下，直流线路传输的有功功率越高，系统的区间振荡阻尼比和区间振荡频率越高。这是因为直流系统不存在功角问题，将交流联络线上的功率更多地分配到功率恒定控制的直流联络线上，能提高混联系统的功角稳定性。

当直流双极运行的交、直流混联系统发生单极闭锁后，直流联络线故障极的过剩功率将影响混联电网的功角稳定性。运用特征分析法对4机2区交直流混联系统单极闭锁前、后不同时间断面进行连续模态分析，计算机电振荡区间模式的阻尼比及振荡频率，绘制成如图5所示的曲线，其中，阻尼数据的小幅波动主要受负荷波动的影响。

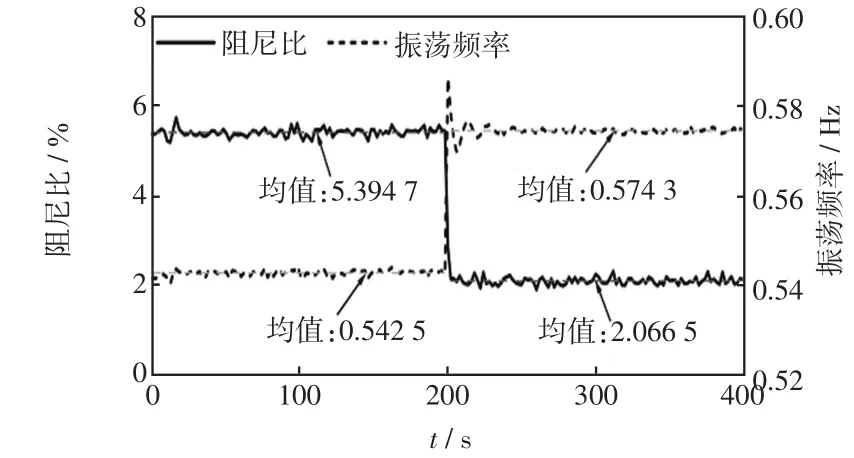
图5 直流单极闭锁前后区间模态参数变化趋势Fig.5 Trends of interval oscillation mode parameters before and after DC unipolar blocking

以系统随机响应数据为源数据，利用SSI算法辨识时变模态参数，图6为直流单极闭锁前后系统区间模式对应的阻尼比和振荡频率的变化曲线及阻尼比的频次分布。

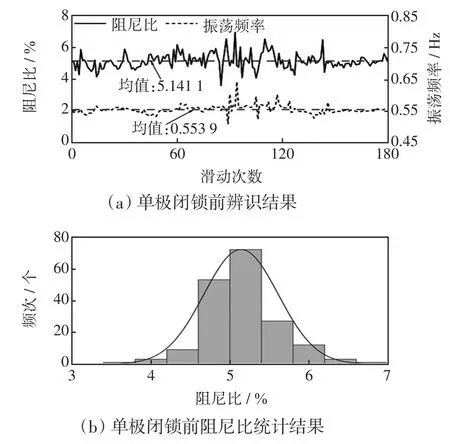
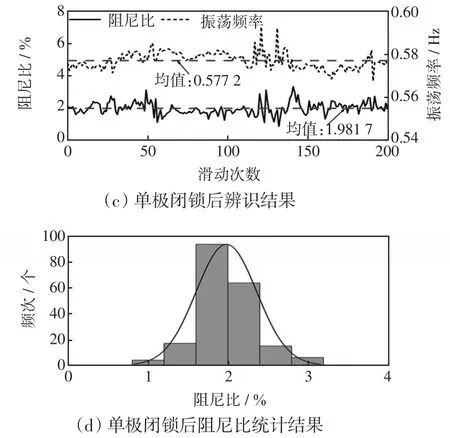
图6 直流单极闭锁前后区间模式辨识结果Fig.6 Results of interval mode identification before and after DC unipolar blocking

表1为传统解析法和SSI算法辨识所得结果。由表1分析可知，SSI算法所得结果与特征分析所得结果接近，能够保证对交、直流混联系统模态参数辨识的精度；同时，SSI算法针对区间振荡模式的辨识结果标准差小，且直流单极闭锁不会影响算法辨识的准确性，表明SSI算法能够有效感知混联系统直流单极闭锁后系统阻尼比的变化。

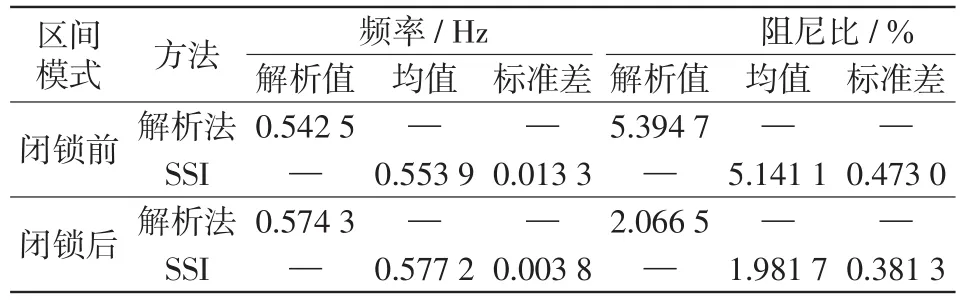
表1 4机2区系统辨识结果统计Tab.1 Statistics of identification result of 4-generator 2-area syste

对比闭锁前、后可知，直流单极闭锁对区间模式影响显著，其振荡频率均值由闭锁前的0.553 9 Hz升至闭锁后的0.577 2 Hz；阻尼比均值由5.141 1%骤降至1.981 7%，系统产生了一个弱阻尼区间振荡模式。

这是因为直流联络线发生单极闭锁后，原本由故障极承担的有功功率转移到与之并联的交流联络线上，联络线断面的直流功率配比大幅下降，导致区间振荡阻尼比骤降。若未经调度，交、直流联络线之间的有功功率配比将处于不合理的工况，系统将可能出现弱阻尼区间振荡，影响系统运行的稳定性。

4.2 16机5区交直流混联系统

在DIGSILENT/PowerFactory中搭建16机5区交直流混联系统进行算例仿真分析[22]，如图7所示。在负荷处添加随机扰动，并设置直流单极闭锁，利用SSI算法对系统的区间振荡模式进行模态辨识，表2和表3为系统各区间模式在单极闭锁前、后的辨识结果。

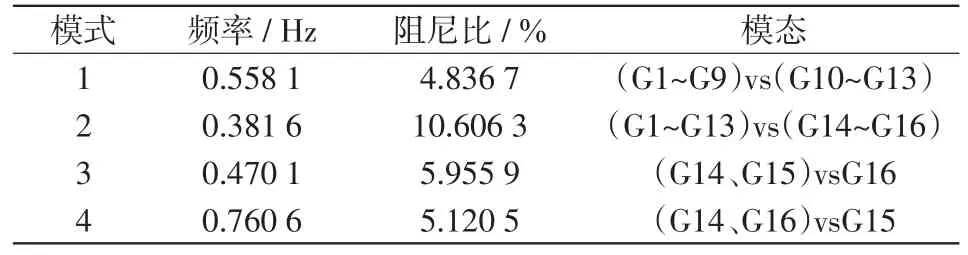
表2 16机5区系统单极闭锁前辨识结果Tab.2 Identification result of 16-generator 5-area system before unipolar blocking

表3 16机5区系统单极闭锁后辨识结果Tab.3 Identification result of 16-generator 5-area system after unipolar blocking

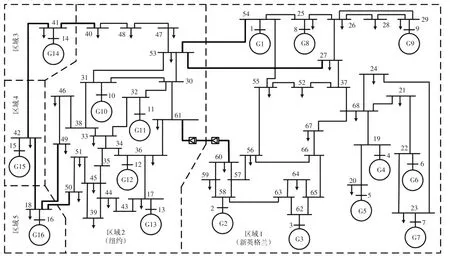
图7 16机5区交直流混联系统Fig.7 16-generator 5-area AC/DC hybrid system

由表2、3可知，对于16机5区交直流混联系统的4个区间模式，直流单极闭锁对区外的区间振荡模式影响较小，对本区的区间振荡模式影响显著，区间模式1的阻尼比由4.836 7%骤降至2.803 2%，混联系统出现弱阻尼区间振荡模式。

利用第2节提出的定点滑窗灵敏度计算方法，计算区域1和区域2各发电机针对区间模式1的阻尼比灵敏度大小。表4为各发电机的阻尼比灵敏度统计结果。其中，筛选出参与有功再调度过程的发电机的递推滑动计算结果如图8所示。

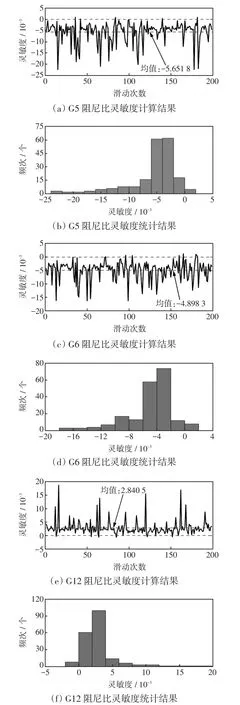
图8 发电机阻尼比灵敏度计算结果Fig.8 Calculation results for damping ratio sensitivity of generators

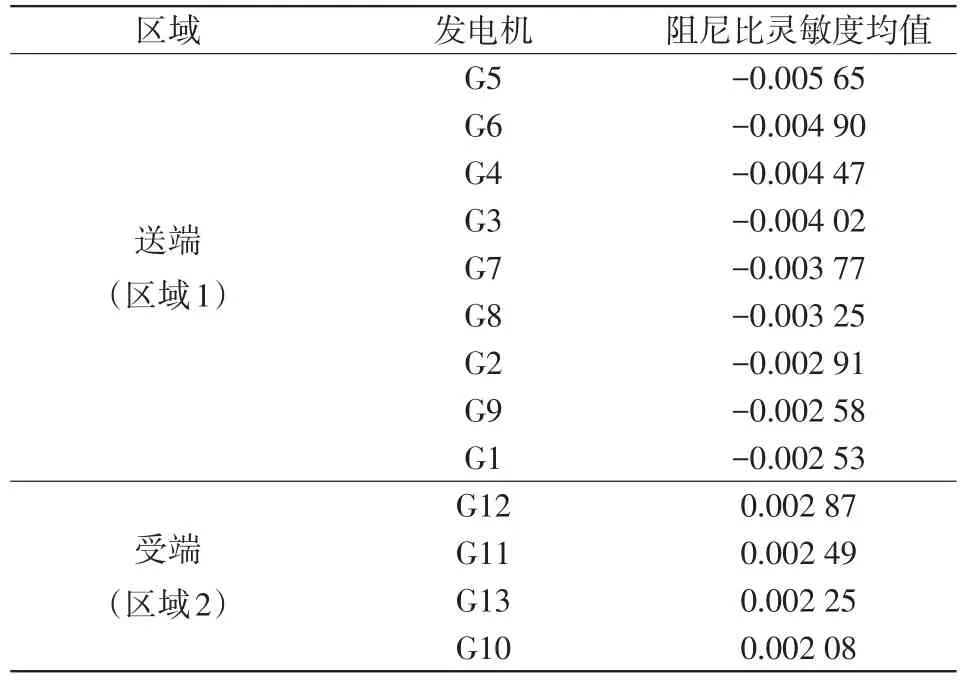
表4 阻尼比灵敏度统计结果Tab.4 Statistical results of damping ratio sensitivity

由图8可知，各发电机阻尼比灵敏度波动范围较大，其统计结果中标准差也较大，主要是由于随机数据波动引起的阻尼比灵敏度计算误差。由频次分布图可知，绝大多数计算结果（85%以上）都集中在灵敏度均值附近的区间，以各发电机阻尼比统计均值作为其灵敏度系数，根据绝对值大小能够做到明显区分同区灵敏度相近的2个发电机。

将定点滑窗摄动法计算所得各发电机阻尼比灵敏度系数归一化处理，并与传统特征值分析法所得归一化灵敏度结果进行对比，其结果如图9所示。由图9可知，本文所提定点滑窗摄动法的阻尼比灵敏度求取结果与解析法所求阻尼比灵敏度排序具有一致性。

图9 定点滑窗摄动算法与解析算法结果对比Fig.9 Comparison of result between fixed-point sliding window perturbation algorithm and analytical algorithm

将送、受端阻尼比灵敏度系数绝对值较大的发电机组合成所有可能，逐步提高再调度量至最大统一调度量（3 p.u.），对应的区间模式阻尼比变化趋势如图10所示。

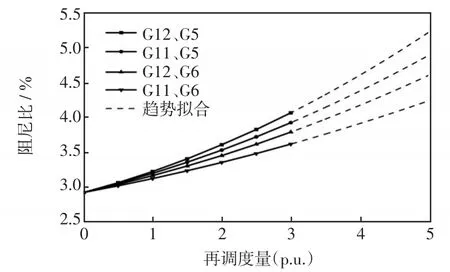
图10 各发电机组合再调度阻尼比变化趋势Fig.10 Trend of damp ratio of generator pairs in redispatches process

由图10可知，相同再调度量下发电机组合{G12，G5}对于系统阻尼比提升效果最大，且随着再调度量的增加区间阻尼比的提升幅度最大。对比表4各发电机阻尼比灵敏度统计结果可知，由受端发电机G12和送端发电机G5组成的发电机对为一次调度下的最优发电机组合，能够使区间振荡阻尼比的提升效果达到最大，做到尽可能地减小机组调节容量及调制次数。上述结果验证了本文所提定点滑窗摄动法计算所得发电机阻尼比-有功灵敏度的有效性。

依据第3节提出的阻尼调制策略，对系统的小干扰稳定性情况加以改善，具体的发电机再调度过程如图11所示。将图11发电机有功及区间阻尼比的变化量进行整理如表5所示。

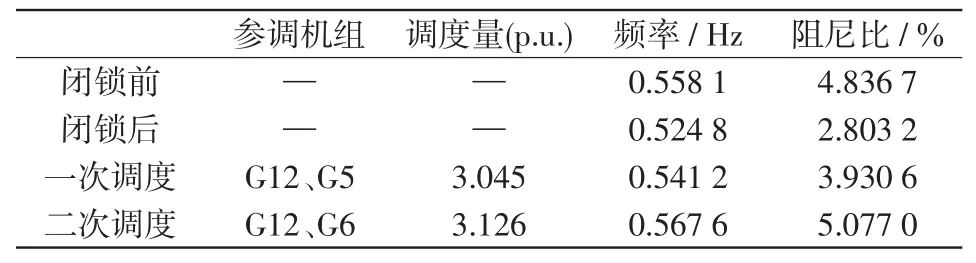
表5 再调度过程阻尼比调制结果Tab.5 Modulation result of damping ratio in redispatches process

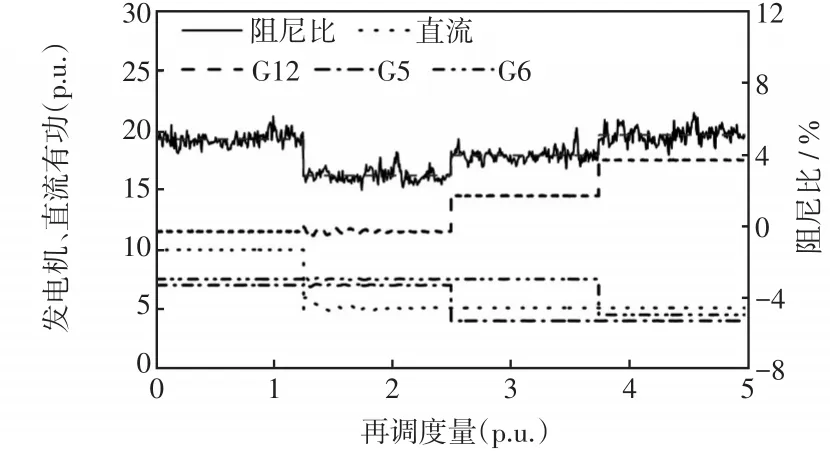
图11 发电机再调度过程Fig.11 Process of generator redispatches

由表5可知，一次调度选择受端发电机G12与送端发电机G5组成调制发电机对，调度量为3.045 p.u.，可将阻尼比由2.803 2%提高到3.930 6%，但仍不能满足小干扰稳定性的要求。进行二次调度，选择受端发电机G12与送端发电机G6组成调制发电机对，调度量为3.126 p.u.，阻尼比由3.930 6%提高到5.077 0%（大于5%），系统满足机电暂态小干扰稳定性要求。由此验证了所提交直流混联电网阻尼调制策略的可行性。

5 结论

本文研究了交、直流混联电网联络线断面直流功率配比及发生直流单极闭锁对系统区间模式的影响。以环境激励下系统动态随机响应为数据集，运用SSI算法对系统模态进行在线辨识，提出基于定点滑窗摄动法计算阻尼比-有功灵敏度以筛选参与调度的发电机组合，通过发电机有功再调度策略改善系统区间振荡阻尼。将该策略运用于算例系统中，得到如下结论。

（1）交、直流混联电网联络线断面上直流功率配比越高，系统区间阻尼比越大；单极闭锁后直流联络线上的功率转移到交流联络线上将可能导致混联系统出现弱阻尼区间模式。

（2）以随机负荷激励下系统随机响应为数据源的SSI算法能够实时有效辨识交直流混联系统的模态。

（3）随机数据驱动下基于定点滑窗摄动法计算的阻尼比-有功灵敏度可有效反映发电机有功波动对区间阻尼比的影响，由此选出敏感发电机组合参与有功再调度的策略可有效提高系统区间模式阻尼水平。