顺应知识内在逻辑 培养数据分析观念

严彪

［摘 要］培养学生的数学核心素养是数学教学的重要目标，数据分析已经成为教学的重要内容之一。以苏教版教材“折线统计图”一课为例，从研究学情、巧用情境、顺应逻辑、结构处理、质疑思辨几个方面，谈如何有效利用教学资源引导学生逐步建构认知体系，感悟数学思想，发展学生的数据分析观念。

［关键词］折线统计图；内在逻辑；数据分析

［中图分类号］ G623.5［文献标识码］ A［文章编号］ 1007-9068（2023）32-0060-03

数据分析观念是《义务教育数学课程标准（2022年版）》的核心概念之一，數据分析观念的培养，对学生的持续发展有重要作用。教师应该重视培养学生的数据分析观念，并以此为抓手，通过课堂教学实践，不断革新传统的教学模式，引导学生自主进行数据分析。以“折线统计图”一课为例，除了让学生了解折线统计图的结构、特点，还要让学生亲历收集、整理数据的过程，对折线统计图中出现的数据进行分析，提取有效信息，并分析、解决相关实际问题，以此培养学生的数据分析能力，促使学生体会统计与生活的联系。

一、研究学情，精准定位

学生在学习数学概念、法则等知识时，一般结合原有的认知结构进行思考，理解新的知识并逐步将其纳入认知结构。也就是说，学生是从已有的生活经验和知识储备出发，去认识和理解与已有知识相似或相近的新知识。因此，在备课的过程中，教师要结合学情，思考知识脉络、理解教学内容、挖掘教学资源，帮助学生理解知识的本质。

在学习“折线统计图”之前，学生已经学过统计表和条形统计图的相关知识，在统计的基本步骤和数据的描述方法上有了一些经验。基于此，本课的教学重点为了解折线统计图的特点及作用，能看懂简单的折线统计图，会分析数据的含义，并能根据统计图做出判断。

二、巧用情境，调动心向

数学是一门抽象的学科，而五年级学生仍以形象思维为主。在数学教学中要寓理于情，就应该让学生在具体的情境中学习，教师应创设与学生生活环境相关的情境，以相关数据为素材，激活学生已有的知识经验，调动学生的兴趣，令学生的学习事半功倍。

【片段1】

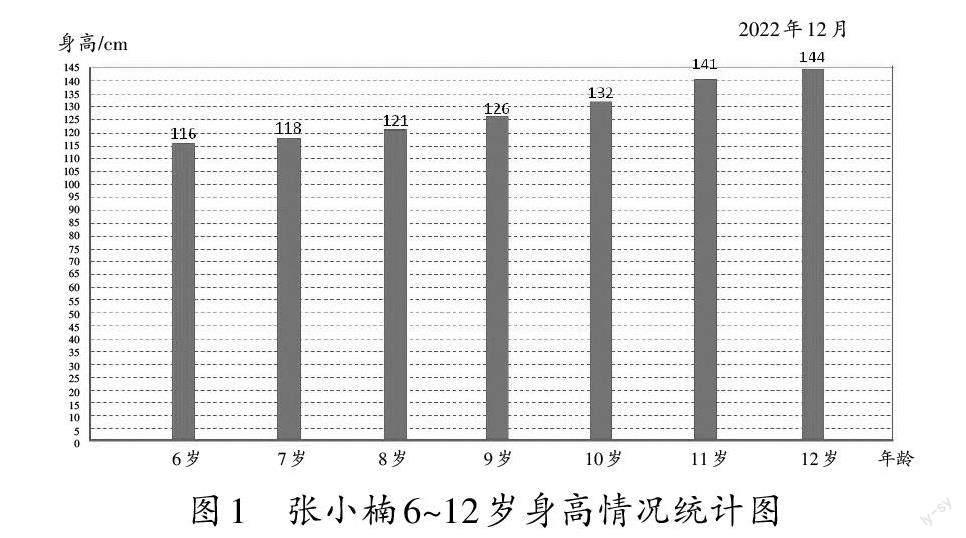
出示（将例题中张小楠6～12岁每年生日的身高数据用文字叙述的形式呈现）：6岁116 cm，7岁118 cm，8岁121 cm，9岁126 cm，10岁132 cm，11岁141 cm，12岁144 cm。

师：第一眼看到这些信息，你有什么感觉？

生1：信息很多也很杂。

师：为了看得更清楚，从数学的角度去统计和描述，可以用哪些方法？

生2：制成统计表。

生3：还可以制成统计图（如图1）。

师：同样的信息，用统计图表示与用统计表表示有什么不同吗？

生4：统计表能有序而清晰地表示数据。通过条形统计图中直条的高低，我们能直观、形象地看出数量的多少。

巧用例题情境的数据，激活学生关于统计的旧知，学生再次经历数据的收集、整理、表达和分析的过程，并沟通统计图表之间的联系。该教学自然地调动学生参与统计活动的兴趣，为后续学习“折线统计图”做好铺垫。

三、顺应逻辑，自然创生

教材的文本信息是静态的，以显性或隐性的方式揭示数学知识或思想方法，同时也为教师的教学提供了可选的素材。教师要站在学生的角度和知识体系的高度，审视新旧知识之间的内在关联，厘清教材内容的内在联系。

为了更好地引导学生将折线统计图的相关知识纳入认知结构中，就要让学生经历知识的产生和发展的过程，这样有利于学生深度理解新知。教师要关注不同统计图之间的联系，以已有的条形统计图为基础，让学生描述数据的变化情况，以遵循数学内在逻辑的问题链为抓手，引导学生独立思考、逐步抽象，再辅以课件的动态演示来实现学生的想法，演化并完善直至形成折线统计图。

【片段2】

师：如果想知道张小楠几岁到几岁身高增长得最快，你打算怎么办？

生1：用前一年直条的最高点和后一年直条的最高点进行比较。

出示图2：

师：怎样才能更清楚地看出点与点之间相差得最多或最少呢？

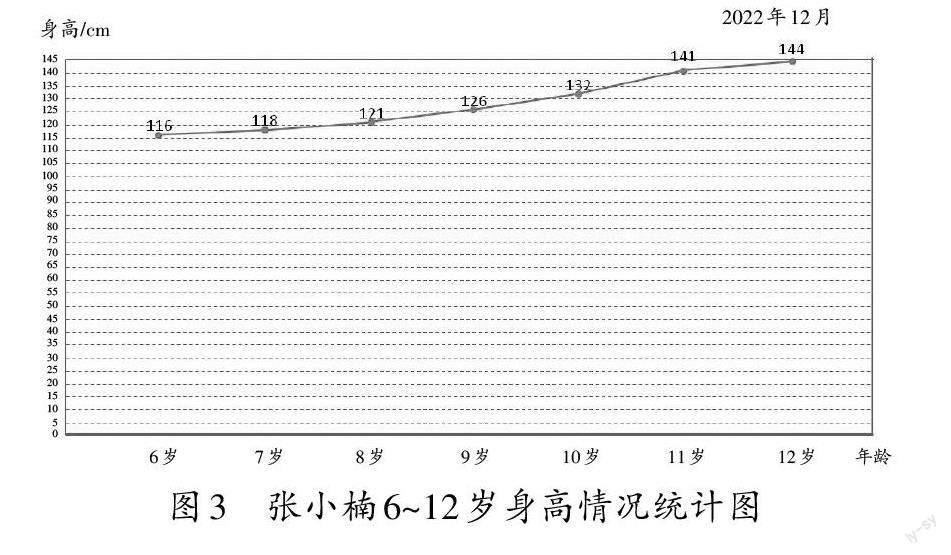
生2：把点连起来。

师（用线段把点依次连接，如图3）：这样就得到了一条曲曲折折的线。

师：这就是我们今天要认识的一种新的统计图，叫折线统计图。图上的点各反映的是几岁生日的身高？怎么才能让信息和相应的点一目了然？

生3：再竖着画一些直线。

师（出示图4）：画了直线后，确实更清楚了。

师：还能不能进一步完善这张折线统计图？

生4：折线的下方空得太多。

师：折线被顶在上方，看起来不舒展，也不清楚，可以怎么改进呢？

生5：可以将没有变化的部分折叠、隐藏起来。

师（出示图5）：现在这样就可以清楚看出身高的变化情况了。

科学合理的学材处理激发了学生的学习兴趣，有效提高了教学效果，也让课堂学习变得丰富多彩。在此过程中，学生经历了折线统计图的产生过程。以“清楚反映身高的变化情况”为抓手，引导学生思考纵轴数据的合理设计，逐步探究、完善，得到完整、规范的折线统计图，为学生后面认识折线统计图的特点和作用埋下了伏笔。

四、结构处理，凸显本质

本课中，条形统计图和折线统计图之间有密切的联系，将两者结合，在比较异同、突出本质的过程中，学生对各个知识点的认识更加清晰，并形成整体认知，从而构建完整的数学知识结构，为后续的学习提供保障。

教师应该将数据分析观念的培养贯穿整个教学活动。在得到规范的折线统计图后，教师要引导学生读图并回答问题，然后结合数据分析发现、提出合情合理的数学问题。在学生交流的过程中，教师应结合事物的客观性，引导学生根据数据进行分析乃至多角度解答。

【片段3】

师：对比折线统计图和条形统计图，它们有什么相同点和不同点？

生1：都有标题、制图日期和数据。

生2：横轴、纵轴表示的信息一样。

生3：条形統计图的直条和折线统计图的点都能表示数量的多少。

生4：从折线统计图中还能看出数量变化的情况——上升的线段倾斜度越大，数据增长得越快。

生5：折线统计图中的线段越长，数据变化越大。

学生在比较条形统计图与折线统计图时，感受到两者在结构、制作等方面有许多相同之处，也都能看出数量的多少，但折线统计图有它独特之处，即通过点反映数据的同时，用线来呈现增减变化的情况。在折线统计图的演化过程中，在读图、画图、分析数据的过程中，学生都能逐步领悟折线统计图的这个特点。

【片段4】

师（出示某地7天的气温记录，略）：请在学习单上完成折线统计图。

师：开始画时，第一步做什么？

生1：描点。

师：为了一眼看出数据，第二步做什么？

生2：标出数据。

生3：最后，再用线段依次连接各点。

师（板书，如图6）：我们依次通过描点、标数和连线这三个步骤，便能完成折线统计图。

通过结构化的教学处理，帮助学生重组、整合零散的知识点，学生获得了属于自己的知识框架，数学知识的学习更加系统，学生改变数学学习碎片化的状况，进一步提高了数学素养。

五、质疑思辨，发展观念

数学教学的基本目标之一就是让学生学会思考，发展数学的思维能力，体现深度思维的数学课堂是有思辨的课堂。学贵有疑，质疑问难是深度思考的表现，是一种数学学习的态度，也是理性精神的集中体现。

充分感受到折线统计图的优点后，学生已经将折线统计图自主纳入原有知识框架，此时可能会单纯地以为“折线统计图最好”。那么，今后分析数据是不是都要用折线统计图呢？适时的追问可以引发学生思考。比如让学生解决如下数学问题：要统计某天一家人摘的水果数量，如果制成统计图，选择折线统计图合理吗？说说理由。对于这一问题的思辨能有效激发学生的探究欲望。学生会对数据进行审视，在体会不同统计图优点的基础上，选择合适的统计图呈现数据，进一步养成数据分析的观念，提升数学素养。若思辨环节在课堂中无法完成，也可以作为课外研究的实践性作业，引导学生将学习从课内延伸至课外，进一步培养学生自主学习的意识和能力。

在大数据时代，用数据来分析、解决现实问题已经成为一种观念，数据分析观念就是数学素养的核心要素之一。要切实发展学生的数据分析观念，就要引导学生了解现实生活中有许多数学问题，可以先做调查研究、收集数据，再通过分析判断，体会数据中蕴涵的丰富信息；了解同样的数据可以有多种不同的呈现方式，要根据问题的背景和实际需要选择合适的方法。教师要选择与学生生活密切相关的素材，让学生根据收集的数据进行统计，以旧知识联系新知识，这样，学生才能在新旧知识的结构化学习中领悟到折线统计图的本质内涵，在数据分析的过程中切实提升数学素养。

【本文系江苏省教学研究“基于测试分析的跟进式改革”重点资助课题“基于监测数据提升区域薄弱学校数学学科教研方式转型实践探索”（2021JY14-CSFX-ZA11）阶段性研究成果。】

（责编 黄 露）