基于NARMAX模型的阀控非对称缸神经网络预测控制

袁 磊，蒋 刚,郝兴安，刘思颂，陈清平，徐文刚

(1.成都理工大学 机电工程学院，四川 成都 610059；2.成都陵川特种工业有限责任公司，四川 成都 610110)

引言

非对称缸具有工作空间小、结构简单、承载能力大等优点，在工程中应用极为广泛[1]。但液压系统具有强非线性及非对称缸结构不对称性，在位置高精度控制时效果不理想。

针对如何提高阀控非对称缸系统的位置控制精度及鲁棒性等问题，科研人员进行了大量研究。许文斌[2]设计了一种自适应滑模控制策略，取得了良好的鲁棒性和位置跟踪精度。彭辉等[3]提出一种含补偿因子的双模糊控制策略，有效解决了非对称缸的控制问题，取得了良好的控制效果，虽然验证了不同频率指令信号下算法的有效性，但是没有考虑变干扰力对阀控非对称缸系统的影响。王云飞等[4]提出了一种基于干扰观测器的控制策略，对系统外部干扰力和流量压力进行观测，提高了非对称缸的跟踪精度。许玲玲等[5]设计了一种终端滑膜控制器，对阀控系统表现出良好的控制效果。孙浩等[6]结合机器学习提出了基于高斯过程的模型预测控制策略，实现了高精度的位置控制且无超调。杨泰春等[7]设计了支持向量机和顺序二次规划算法的模型预测控制器，实现了多约束条件下液压缸的快速和精确控制。王向才[8]在基于传统模型预测基础上，融合了布谷鸟改进PID算法，验证了对不同指令信号良好的跟踪效果。戚永委等[9]基于阀控非对称缸的Hammerstein模型，结合二次序列算法验证了该策略良好的跟踪性能和稳定性。

本研究提出一种QPSO-NNMPC控制策略，针对阀控非对称缸系统设计了基于QPSO-NNMPC的控制系统，结合数值仿真验证该控制策略的有效性。

1 阀控非对称缸的NARMAX模型

如图1所示，非对称缸结构不对称，在伸缩过程中，流量增益、流量压力系数、液压固有频率、液压阻尼比等参数不同[9]，难以建立统一的传递函数，传统方法控制难度加大，因此采用QPSO-NNMPC控制策略进行控制。

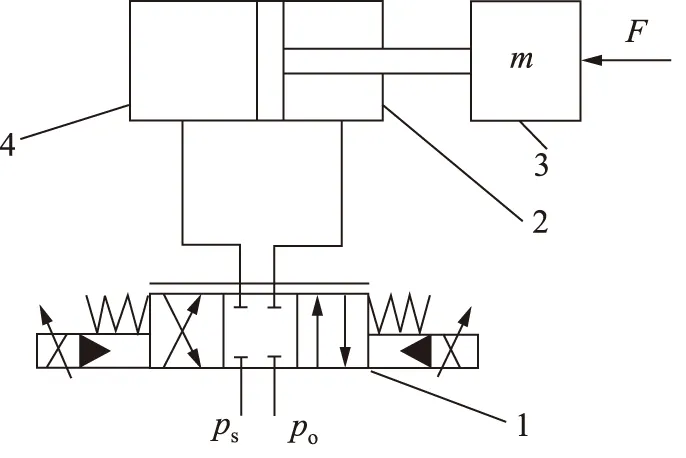
1.伺服阀 2.有杆腔 3.负载 4.无杆腔图1 阀控非对称缸工作原理图Fig.1 Working principle diagram of valve-controlled asymmetric cylinder

选用伺服阀为高频伺服阀，其频率远大于阀控非对称缸系统的固有频率，伺服阀的传递函数可由比例环节表示，将该系统简化为三阶系统[10]。用NARMAX模型描述该系统的动态模型[11]，忽略噪声项，该系统的NARMAX模型表示为：

y(k+1)=f[y(k),y(k-1),…,y(k-b+1),

u(k),u(k-1),u(k-a+1)]

(1)

式中，y(k)为当前时刻液压缸位移输出；y(k-1),…,y(k-a+1)为历史时刻液压缸位移输出；u(k)为当前输入信号；u(k-1),…,u(k-b+1)为历史输入信号；a为输入的延迟阶次；b为输出的延迟阶次；f(·)为非线性函数。

2 神经网络预测控制

如图2所示，NNMPC由阀控非对称缸、神经网络预测模型和非线性优化3部分组成。

图2 NNMPC结构Fig.2 NNMPC structure

神经网络预测模型利用PSO-BP根据NARMAX模型对阀控非对称缸系统在线预测控制时域P内的输出，通过输出误差确定目标函数，非线性优化利用QPSO对目标函数在线寻优，得到该系统的最优输入量。

2.1 PSO-BP神经网络预测模型

BP神经网络有两个缺点：收敛速度慢及容易陷入局部最优[12]，导致预测模型精度与效率较低。利用PSO改进BP神经网络，提升预测模型的精度与寻优效率。

神经网络预测模型基于NARMAX模型利用PSO-BP在线预测。如图3所示，在k时刻根据阀控对称缸系统历史输入信号u(k-1),…u(k-a)、液压缸当前时刻位移y(k)及液压缸历史位移y(k-1),…u(k-b)作为网络输入，基于NARMAX模型预测液压缸当前时刻位移yN(k)，利用预测误差训练预测模型，用训练好的预测模型递推得到预测时域P内液压缸位移。

图3 PSO-BP神经网络预测模型Fig.3 PSO-BP neural network prediction model

输入层层数为a+b+1；隐含层层数为M；输出层层数为1。

PSO是基于种群的进化算法，全局寻优能力较强。种群中的粒子代表优化问题的解，粒子朝着个体极值和全局极值方向移动，进而搜索出最优解[13]。

设优化空间维度为D，D为BP神经网络权值和阈值矩阵的总元素个数。第i个粒子速度更新公式为：

(2)

式中,SiD—— 粒子的新速度

k—— 惯性系数

b1,b2—— 常数

rand() —— (0～1)的随机函数

Pg—— 历史个体极值

Pq—— 历史群体极值

由向量运算法则，粒子的更新公式为：

(3)

2.2 输出预测

基于模型预测思想，由训练好的PSO-BP预测模型得到预测时域P内的系统输出，由NARMAX模型，其递推公式为：

(4)

2.3 非线性优化

非线性优化模块根据目标函数确定系统最优控制量。预测时域内输出误差E：

E=Yd-Y

(5)

式中，Yd=[yd(k+1),yd(k+2),…,yd(k+P)]为预测时域P内的期望输出；Y=[y(k+1),y(k+2),…,y(k+P)]为预测时域P内的预测输出。

取二次型目标函数为：

(6)

式中，Q，R——RP*P权重矩阵

du—— 当前时刻控制时域的控制量与上一时刻控制时域的控制量的差值矩阵

dumax，dumin—— du最大与最小值

1) 量子行为粒子群算法

PSO虽然收敛性快，但是不能全概率收敛，有概率陷入局部最优[14]。但对于阀控非对缸这种强非线性和时滞性的系统，最优控制量必须是全局最优解，因此对PSO进行改进。

QPSO是结合量子理论的改进PSO，具有非常强的随机性，能以全概率收敛,在量子空间中，粒子的状态只能用波函数来描述，波函数由薛定谔方程求得，最后采用蒙特卡罗方法求出全局最优解[15]。

设优化空间的维度为预测时域P，种群有M个粒子。在t时刻，粒子的位置可以表示为：

Xi(t)=[Xi,1(t),Xi,2(t),…,Xi,M(t)],

(i=1,2,…,M)

(7)

根据PSO粒子收敛行为分析，必然存在Gi,j为吸引子，其坐标为：

Gi,j=ui,j(t)Pgi,j(t)+(1-ui,j(t))Pqj(t)

(8)

式中，ui,j(t)为(0～1)均为分布的随机数；特征长度Li,j(t)为：

Li,j(t)=2a|Cj(t)-Xi,j(t)|

(9)

式中,Cj(t) —— 平均个体最优位置

根据薛定谔方程，第i个粒子每一维波函数为：

(10)

其对应的概率分布函数为：

(11)

由蒙特卡罗方法，可得第i个粒子第j维的进化方程为：

(12)

QPSO流程图如图4所示。

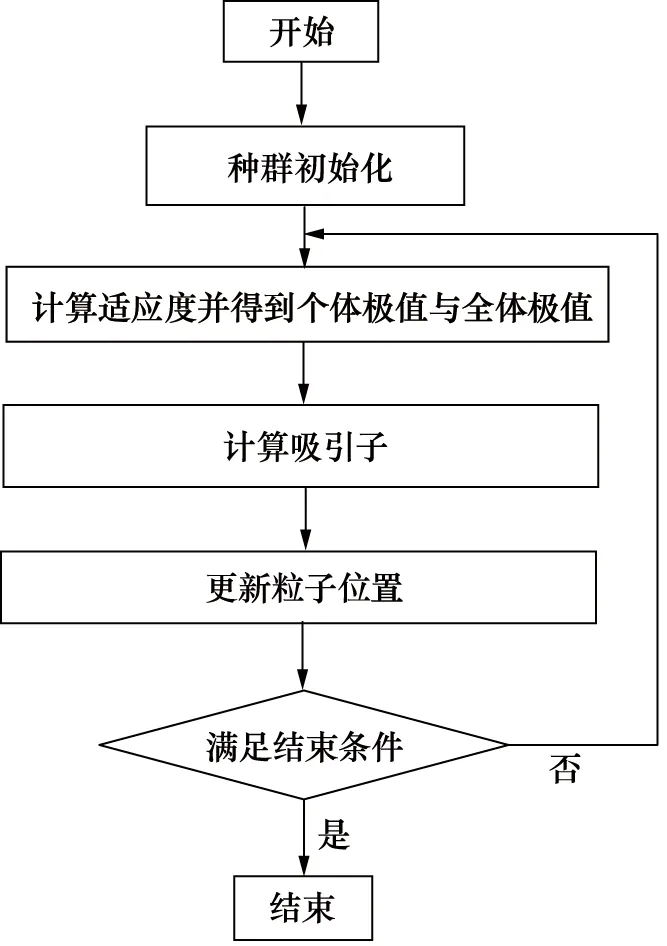
图4 QPSO算法流程图Fig.4 QPSO algorithm flow chart

3 仿真分析

为验证QPSO-NNMPC控制策略的有效性，分别利用AMESim与Simulink的优势进行联合仿真。结合液压缸的工作环境，分析在不同频率期望信号、不施加变干扰力与施加变干扰力条件下，分别采用PID、PSO-NNMPC及QPOS-NNMPC 3种控制算法控制阀控液压缸系统，对比液压缸对期望信号的跟踪效果。

3.1 仿真模型搭建

在AMESim中搭建阀控非对称缸液压系统，如图5所示，主要液压元件参数设置如表1所示。

在Simlink中搭建神经网络预测控制系统，如图6所示。

3.2 结果分析

设置期望信号为yd=40sin(2πft)。其幅值为40 mm，频率f分别为0.1 Hz和0.5 Hz。无干扰力，频率为0.1 Hz的位移跟踪和跟踪误差如图7和图8所示。

1.液压泵 2.电机 3.溢流阀 4.信号取反器 5.非对称缸 6.活塞及负等效质量 7.位移传感器 8.干扰力转换器 9.伺服阀 10.油箱图5 阀控非对称缸液压系统Fig.5 Valve-controlled asymmetric cylinder hydraulic system

表1 阀控非对称缸液压系统主要参数Tab.1 Main parameters of valve-controlled asymmetric cylinder hydraulic system

图6 QPSO-NNMP仿真模型Fig.6 QPSO-NNMP simulation model

图7 f=0.1 Hz无干扰力时位移跟踪图Fig.7 Displacement tracking diagram when f=0.1 Hz without disturbing force

图8 f=0.1 Hz无干扰力时跟踪误差图Fig.8 Tracking error diagram when f=0.1 Hz without disturbing force

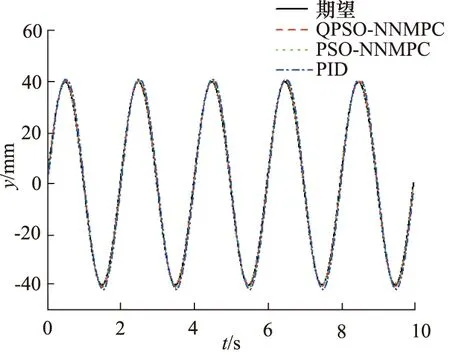
图9 f=0.5 Hz无干扰力时位移跟踪图Fig.9 Displacement tracking diagram when f=0.5 Hz without disturbing force

无干扰力，频率为0.5 Hz时位移跟踪和跟踪误差如图9和图10所示。

根据图7～图10，无干扰力、不同频率期望信号时，液压缸的跟踪误差如表2所示。

根据表2误差比较，当频率设置为0.1 Hz时，PSO-NNMPC控制精度较PID提高56.8%，QPSO-NNMPC控制精度较PID提高60%。当频率设置为0.5 Hz时，PSO-NNMPC控制精度较PID提高69.5%，QPSO-NNMPC控制精度较PID提高75.2%。对比3种控制策略的仿真结果，在无干扰力的情况下，QPSO-NNMPC控制精度最高，PSO-NNMPC控制精度次之，PID控制精度最差。

当施加变干扰力F=500+300sin(2πt)，其干扰力如图11所示。

施加变干扰力F，频率f为0.1 Hz时位移跟踪和跟踪误差如图12和图13所示。

图10 f=0.5 Hz无干扰力时跟踪误差图Fig.10 Tracking error diagram when f=0.5 Hz without disturbing force

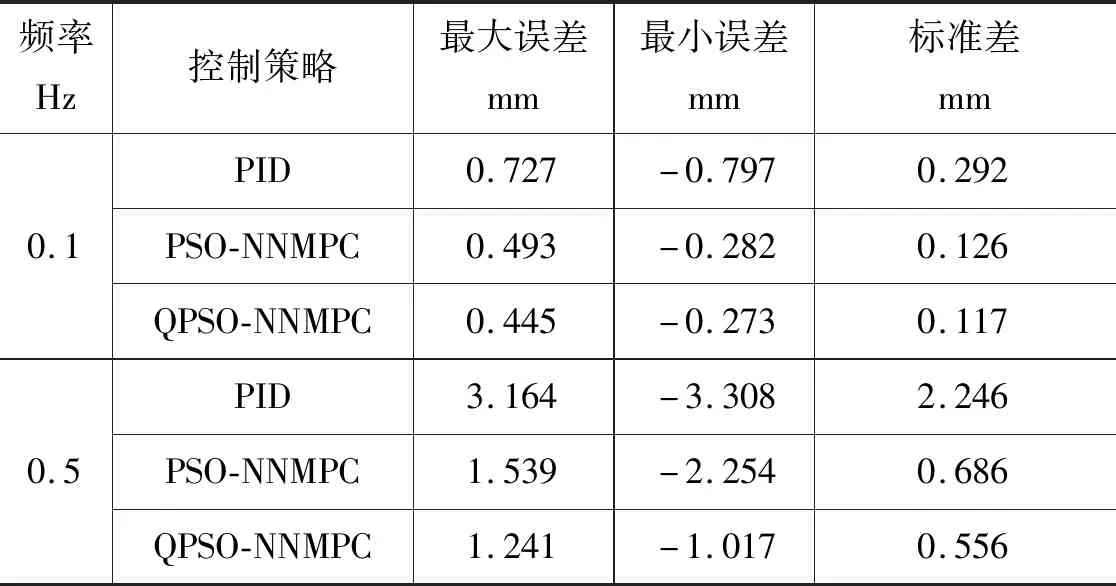
表2 无干扰力、不同频率时跟踪误差表Tab.2 Tracking error table with no interference and different frequencies

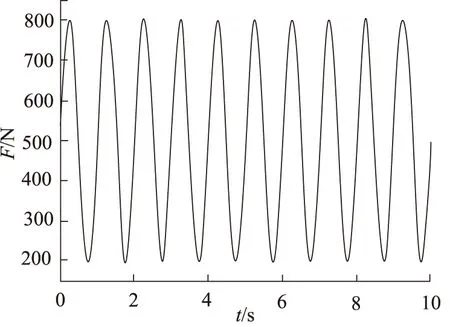
图11 变干扰力Fig.11 Variable interference force

图12 f=0.1 Hz变干扰力时位移跟踪图Fig.12 Displacement tracking diagram when f=0.1 Hz changes disturbance force

图13 f=0.1 Hz变干扰力时跟踪误差图Fig.13 Tracking error diagram when f=0.1 Hz variable interference force

施加变干扰力F，频率f为0.5 Hz时位移跟踪和跟踪误差如图14和图15所示。

根据图12～图15，在变干扰力、不同频率期望信号时液压缸的跟踪误差如表3所示。

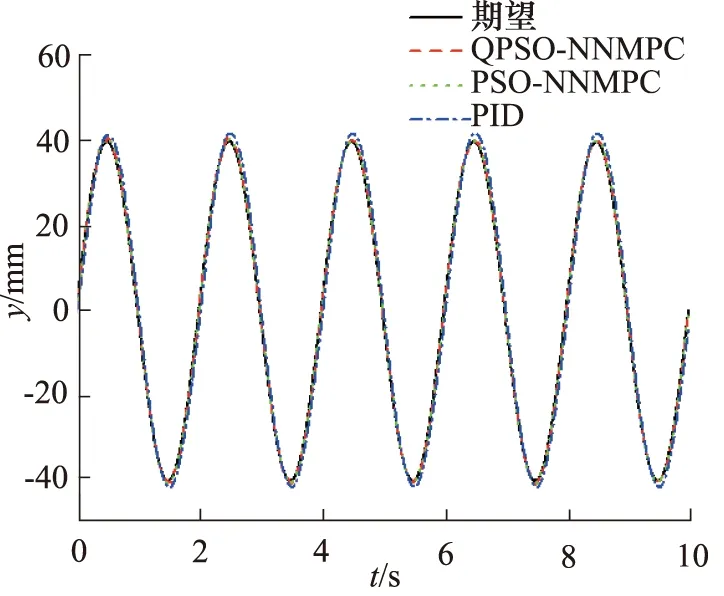
图14 f=0.5 Hz变干扰力时位移跟踪图Fig.14 Displacement tracking diagram when f=0.5 Hz changes disturbance force

图15 f=0.5 Hz变干扰力时跟踪误差图Fig.15 Tracking error diagram when f=0.5 Hz changing disturbance force

表3 变干扰力、不同频率时跟踪误差表Tab.3 Tracking error table of variable interference force and different frequencies

从表3可以看出，施加变干扰力时，3种控制算法的跟踪精度都有一定程度的下降,其中PID控制精度最差。当期望信号频率为0.1 Hz时，PSO-NNMPC控制精度较PID提高47.4%；QPSO-NNMPC控制精度较PID提高55%。当期望信号频率为0.5 Hz时，PID出现不稳定，PSO-NNMPC控制精度较PID提高70.9%；QPSO-NNMPC控制精度较PID提高80%。对比3种控制策略的仿真结果，在变干扰力的情况下，QPSO-NNMPC控制精度最高，PSO-NNMPC控制精度次之，PID控制精度最差。

对比表2和表3，在施加变干扰力和不施加干扰力情况下，对比3种控制策略的控制精度。期望信号频率为0.1 Hz，PID控制精度降低34.6%；PSO-NNMPC控制精度降低22.2%；QPSO-NNMPC控制精度降低13.6%。期望信号频率为0.5 Hz时，PID控制精度降低28.7%；PSO-NNMPC控制精度降低18%；QPSO-NNMPC控制精度降低9.3%。根据比较QPSO-NNMPC表现出良好的鲁棒性。

4 结论

本研究对阀控非对称缸系统轨迹跟踪控制问题做了相关研究，提出了一种QPSO-NNMPC控制策略，仿真结果表明，该策略有效提升了阀控非对称缸系统的位置控制精度。在液压缸高频运动和施加变干扰力的情况下，QPSO-NNMPC具有较好的控制精度和鲁棒性。