浅析高速连接器阻抗优化

王 超，钟茂萍，江 涛

(四川华丰科技股份有限公司，四川绵阳，621001)

1 引言

随着5G技术的日益发展，通讯设备不断升级换代，信号传输速率不断上升，系统链路信号完整性要求进一步提高。高速连接器作为系统链路至关重要的一环，连接器的性能要求也是越来越严苛，作为连接器厂商，如何保证产品设计及加工性能是一个很大的挑战。

对于高速连接器来说，跑高速的信号基本都是差分信号，由于连接器结构复杂，随着信号上升时间的不断减小，阻抗匹配难度也越来越大，本文通过解析差分阻抗原理，介绍了差分阻抗优化较常用的优化手段。

2 差分线的阻抗[1]

常用的信号传输分为单端信号和差分信号，差分信号由两根单端信号构成，发射器传输差分信号时，会将单端信号拆分成两个信号幅值相等相位相反的两个信号，再由接收器识别转化为单端信号。简单来说，接收器会将两个单端信号做一个减法，得到的信号幅值将是单个信号的两倍；差分信号由于抗干扰能力强，在高速信号传输中被广泛应用。

从理论上来说，任何两根走线都可以构成差分对，可实际上，我们设计中的差分信号都会符合对称原则，这个对称包含以下几个条件：

1) 两根线具有相同并且恒定的阻抗，保证两根线上的反射尽量小，在减少因反射造成的信号失真的同时，也尽量避免因两根线反射不同，导致多余共模分量出现的情况。

2) 两根线的线宽，以及走线之间的间距、介质等保持恒定。

3) 两根线的线长与延时相同，延时不同会导致共模信号的增加，使信号变差。

为了简化问题，我们假定差分线符合上述条件，并且两根线之间没有耦合，这时，电路中电压与电流如图1所示。

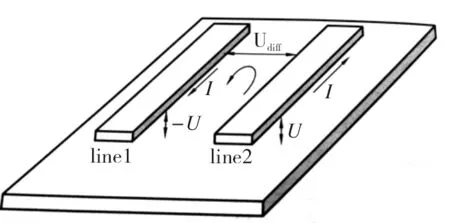
图1 差分信号

对于差分信号来说，可以认为构成差分线的两根单线上的电压幅度相等，且互为相反数，电流大小相等，方向相反。差分信号电压等于两倍单端电压，电流则像构成了一个回路，其大小和单线电流大小相等，于是形成了下列公式：

Z0=U/I

Zdiff=Udiff/I=2U/I=2Z0

式中，Z0为单根传输线的特征阻抗；Zdiff为差分传输线的差分阻抗；U为信号线与返回路径之间的电压；I为流经信号线与返回路径之间的电流；Udiff为差分传输线的差分电压。

可以看到，对于没有耦合的差分线来说，其差分阻抗等于两倍单线阻抗，也可理解为两线单线阻抗的串联。

对于共模信号，共模电压与单线电压相等，共模电流为单线电流的两倍，所以有：

Z0=U/I

Zcomm=Ucomm/I=0.5U/I=0.5Z0

式中，Zcomm为差分传输线的共模阻抗；Ucomm为差分传输线的共模电压。

所以，共模阻抗等于单线阻抗的一半，也可以理解为两根单线阻抗的并联。

但就实际情况而言，大部分差分线是存在耦合的，而我们使用相同的结构后由于耦合因数，实际的差分阻抗会变小，如图2所示为一高速连接器中的差分和单端仿真阻抗值。

图2 典型差分线单端和差分阻抗

简而言之，差分阻抗的一半是小于单线阻抗的。

对于传输线来说，在信号传输过程中，每个单位长度△X都会不断产生小电容CL，所以传输线的电容大小是它们的乘积：

C=CL×△X

而电流大小就是单位时间内加在每个电容上的电量，可得以下公式：

I=Q/△t=C×U/(△X/V)=CL△XVU/△X=CLVU

式中，I是信号电流大小(A)；Q是每个小电容电量(C)，△t是传输至两个小电容之间所需时间(S)，C是每个小电容的容值(F)，U是信号的电压(V)，△X是每个小电容长度(M)，v是信号传输速度(m/s)；CL是单位长度电容大小(F/m)。

Z0=U/I =U/CLVU=1/CLV

从公式中可知，阻抗与传输线单位电容成反比。

3 差分阻抗对信号完整性的影响

差分阻抗和上升时间强相关，上升时间越短，阻抗波动越大，阻抗越难控制；上升时间和带宽成反比，所以对于速率越高的产品，特别是目前流行的56G和112G产品，阻抗波动会越大，匹配难度增加。

阻抗的波动会直接影响回波损耗值，回波损耗代表信号的反射，波动越大，反射越大，回波损耗越差；反射能量多了，接受到的能量就会变少，所以插损也会变差，如下为90欧姆的阻抗匹配值对应的插损和回损值。

图3 不同阻抗对应的插损和回损值

从图3不同阻抗对应的插损和回损可以看出，1号线的阻抗在90欧姆左右波动，明显优于2号线，插损和回损1号线也明显比2号线好，所以阻抗匹配有利于减少反射，提升系统的损耗裕量。

4 影响差分阻抗的因素

4.1 导体横截面积的变化

导体横截面积增大会导致阻抗变低，相反阻抗变高；阻抗与导体横截面积的变化类似于导体电阻，这是因为阻抗公司中的电流与导体本身的电容成正比，导电横截面积的增大，变相增大了导体电容，从而降低了阻抗。

如下图4我们建立一个差分模型，在差分间距0.3mm和回流地间距0.2mm不变的情况下，改变线宽0.5mm大小，分别对比线宽0.4mm、0.5mm、0.6mm阻抗的变化值。

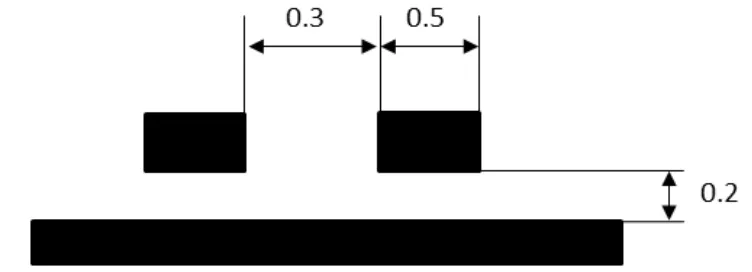
图4 差分模型

阻抗仿真结果如下图5：

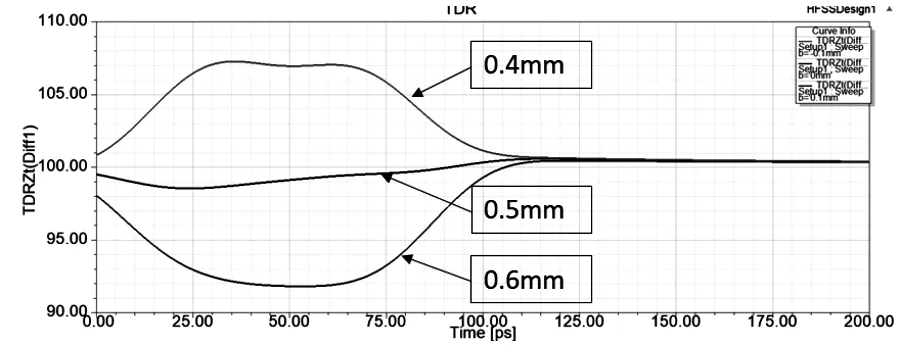
图5 不同线宽的阻抗

从仿真结果可知，只改变线宽大小，线宽越宽，阻抗越小，同理，改变走线厚度也是同样道理，只要导体横截面积发生变化，都会导致阻抗的变化；所以我们在连接器调试阻抗时，经常会尝试去调整线宽改变阻抗，以达到我们的需求值。

4.2 信号线间距变化

当信号线之间间距发生变化时，信号线之间的耦合也会发生变化，间距越小，耦合越强，则信号线感受到的电容越大，阻抗就会越低。所以减小信号线间距阻抗会变低，加大间距阻抗则会升高。

我们同样使用图4的仿真模型，在其他尺寸不变的情况下，改变间距0.3mm的数值，我们分别仿真间距0.2mm，0.3mm，0.4mm对比仿真结果，仿真结果如下图6：

图6 两种不同的串扰模型

从仿真结果看出，线距越大阻抗越高，所以调整间距也是匹配阻抗的重要手段之一。

4.3 信号线与回流地的间距

我们经常看到，高速信号都伴有回流地，回流地与信号线的间距对阻抗也有很明显的影响，信号线与回流地也存在耦合，耦合越强，电容越大，阻抗越低。

我们同样使用图4的仿真模型，在其他尺寸不变的情况下，改变回流地间距0.2mm的数值，我们分别仿真间距0.15mm，0.2mm，0.25mm对比仿真结果，仿真结果如下图7：

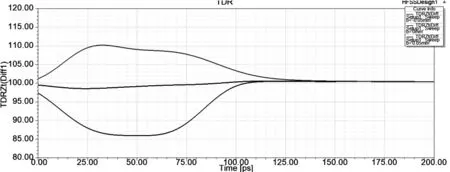
图7 不同回流间距的阻抗

从仿真结果可以看出，回流间距对阻抗影响比较大，间距越小阻抗越低，在调整回流地间距时需要考虑信号线可加工性，一般信号线冲模对线宽有最小值要求，也需要考虑串扰等其他指标的影响。

回流地的形式较多，图4为PCB中厂家的微带线，另外还有如下图7中的带状线和射频同轴类，回流地的方式不同对阻抗的影响也不同，回流地的完整对串扰的影响也较大。

图8 厂家差分信号屏蔽种类

回流地的形式有很多种，连接器的回流路径较复杂，高速连接器一段走线屏蔽经常有多种组合形态，调整阻抗时需随机应变，但尽量做到屏蔽完整。

4.4 介质DK值的影响

通常，连接器信号与信号之间都有绝缘介质，其目的是固定信号与信号的位置隔离信号防止短路，介质DK值会影响绝缘电阻及耐电压，对阻抗也有很明显的影响。

Dk反映的是绝缘体如何积蓄电能，从而使电子元件相互绝缘，并与地面绝缘。Dk是两种材料电容值的比：一种作为介电物质的电容与空气或真空作为介电物质的电容之比，空气的DK值为1.0，是绝缘介质中DK值最小的。而从前面阻抗公式中可知，阻抗与单位电容成反比，DK值越大，电容则越大，则阻抗就会越低。

如下图9建立一仿真模型，在其他条件不变的情况下改变绝缘介质的DK值，分别设置2.8，3.0，3.2，对比阻抗曲线。

图9 仿真模型

仿真结果：

图10 不同DK值阻抗仿真结果

从仿真结果可以看出，阻抗对DK值大小变化很敏感，DK越大阻抗越低，产品设计中选择合适的DK值也是非常重要；在类似微带线结构中，绝缘介质厚度也会对阻抗产生明显的影响，厚度影响也不是无限的，这是因为绝缘介质较薄时，信号线会同时感受的绝缘介质和空气的DK值，绝缘介质和空气DK混合后会导致信号感受到的DK值介于空气与绝缘介质之间，当达到一定值后就不再影响阻抗了，所以调整绝缘厚度也是调整阻抗的重要手段。

5 常用的阻抗计算软件

产品设计初期，当大致结构出来后，我们回去匹配信号线阻抗值，如果通过三维电磁场软件仿真效率太慢，这时候我们可以借用一些2D软件来计算阻抗值，比如SI9000、或者Allegro、Altium，HFSS自带的计算模块，我们以SI9000软件计算为例，来匹配一段连接器走线阻抗值到90欧姆。

建立如下连接器中常见模型，模型中有信号端子埋在塑胶，也有暴露在空气中部分，也有无屏蔽部分，如下分为三段：

对于初始结构，我们假定信号料号0.15mm，屏蔽与信号0.25mm，信号上半部绝缘厚度0.55mm，绝缘介质DK值3.0，我们利用SI9000进行初步仿真，确定线宽、线距等。

图11 仿真模型

先确定第一段，如下：

图12 第一段计算值

从仿真中可确定第一段线宽为0.21mm，线距0.3mm。

第二段计算值如下：

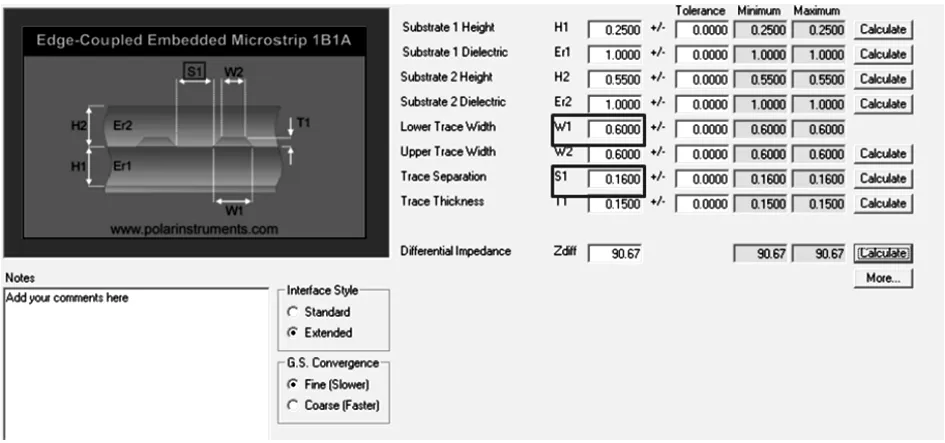
图13 第二段计算值

从仿真中可确定第二段线宽为0.6mm，线距0.16mm。

第三段计算值如下：

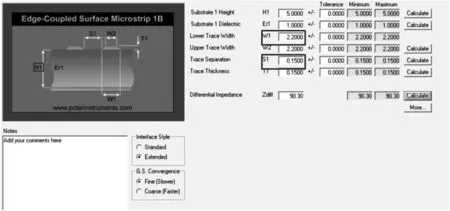
图14 第三段计算值

从仿真中可确定第三段线宽为2.2mm，线距0.15mm。

按照计算的数值结果，我们更新3D模型，如下：

图15 更新后仿真模型

图16 匹配后仿真结果

当然更新后第三段线宽比较夸张，我们实际产品设计时要给第三段匹配回流地，避免出现回流地缺失，而且回流地缺失也会引起串扰的问题；我们将整个模型带入HFSS中进行仿真，看整段阻抗匹配结果是否一致：

从仿真结果可以看出，匹配阻抗最低在83欧姆左右，与实际要求90欧姆有7欧姆偏差，偏差也不是很大，软件只是初步计算，我们需要根据三维电磁场软件仿真结果微调线宽，这样可以大大减小调试计算量。

所以，我们在产品设计时尽量多使用2D仿真软件计算走线阻抗值，有助于提高工作效率。

6 结束语

高速连接器结构复杂，考虑的因素众多，阻抗的不连续点非常多，对于信号完整性工程师来说，必须要识别影响阻抗的因素，好做出正确的调整；也需要多利用相关软件仿真，达到快速匹配阻抗的目的。