基于ANSYS Workbench配气滑阀多参数优化设计

梁 浩

(珠海格力电器股份有限公司，广东 珠海 519070)

0 引言

气动发动机是以高压空气在气缸内膨胀做功，带动活塞杆往返运动，为负载提供动力。配气滑阀是整个配气过程的核心部件，如图1所示，进气时气缸活塞带动滑阀阀杆运动，直至阀杆将进口关闭；当气缸膨胀做功完毕后，活塞返回，同时带动滑阀阀杆返回，完成一次配气。在高压气体经过滑阀配气的过程中，随着配气滑阀开度的减小，涡旋越大，造成的节流损失和能量耗散就越多。由于导杆的存在，使得导杆后部出现扰流。因此，滑阀进、出口和导杆是配气滑阀造成能量损失较大的部位。由于节流损失不可能消除，所以通过阀体优化，尽可能地降低不可逆损失，从而提高配气效率。

图1 配气系统结构图

1 阀体的设计

阀体的设计主要参照换向阀的设计，并作适当修正，其主要是确定进气口、出气口、阀芯直径。进、出口直径d0：

(1)

其中：qs─阀的额定流量，m3/s；v0─阀进、出气体的允许流速[1]。

D=(1.4～1.7)·d0

(2)

阀体的基本参数见表1。

表1 阀体的基本参数

阀杆设计与阀体配套，阀芯外径确定，则阀杆的直径与阀体阀芯外径相等，阀杆对密封性有一定的要求，滑阀总体设计图如图2所示。

图2 滑阀总体设计图

2 配气滑阀的优化

2.1 滑阀阀芯的参数化模型

由于节流作用，流体通过通流截面时，气体速度增加，在拐角形成涡旋，造成能量耗散。因此，在阀芯进口和出口增加圆角导流，让气流以最小阻力经过阀芯通道。同时，为了消除导杆的能量损失，将不采用导杆形式，图3为改进滑阀的结构示意图。

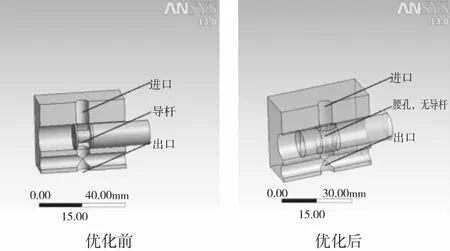
图3 优化前后滑阀的三维图

其中阀芯腰孔的形状及尺寸如图4所示。

(1)土壤水中离子浓度。离子浓度越低，潜在破坏风险越高。分散性土在离子浓度很低时，是最容易被水侵蚀的，如雨水。

图4 腰孔示意图

腰孔的半径R和H决定了腰孔的大小，L的长度决定了进出口圆角的倾斜度和大小。腰孔省去了原来滑阀内部的导杆，彻底消除由导杆造成的能量损失。同时在进出口采用倒圆角，实现气流平滑流入和流出，尽可能减小损失。将上述参数R、H和L作为滑阀优化的可变参数，运用Workbench的参数化建模和优化设计，实现滑阀的多参数优化设计。

2.2 基于Workbench的系统优化

在ANSYS Workbench中，产品性能的优化设计是通过Design Explorer来实现的。Design Explore 主要是在产品设计生产之前分析产品对性能的不确定因素，尽可能地提高产品的性能。

在Workbench的Design Modeler中，进行配气滑阀的参数化建模，取R、H和L为可变参数。在CFD的后处理软件中，将相应的输出参数通过设置作为优化的目标参数。本文主要是研究配气系统配气过程的能量损失，因此采用滑阀进出口压差和滑阀的熵增为优化目标参数，在CFD Post中定义滑阀进出口压差和配气滑阀熵增的表达式，并通过Use as Workbench Output Parameter 将其作为DX的输出参数，表达式如下：

Pressuredrop=ave(StaticPressure)@interface2-ave(StaticPressure)@interface2 Entropy=1006[Jkg^-1K^-1]*ln((areaAve(Temperature)@interface1)/(areaAve(Temperature)@interface2))+287[Jkg^-1K^-1]*ln((areaAve(Pressure)@interface1)/(areaAve(Pressure)@interface2))

2.2.1 响应曲面的优化

在Design Explore中，可以根据需要观察到输入参数的影响，它们都是通过响应曲面的形式来反映输入输出参数之间的相互关系(即响应图标)，它支持实验数据法。运算结束后，响应曲面曲线的拟合是通过设计点完成的。

响应曲面是基于输入参数的数目，通过一定数目的设计点建立的。通过实验设计或DOE的具体方法，可以产生具体的设计点和设计点的个数。将这些点通过Fluent求解，根据参数可以拟合出输出结果的响应曲面，并保证不存在“硬”解。响应曲面的输入参数对应的输出值是连续变化的，并不是离散的赋值，具有较强的适应性。

滑阀确定性分析的参数变化如下：

R：3 to 4

H： 1 to 3

L： 4.5 to 5.5

DOE法不指定具体参数使用点的数目，而是通过具体方法将提供有用的点。拟合曲面可以通过设计点来拟合，而且设计点的数目越多，拟合的曲面精度越高，越准确，但计算的时间也越多。在Design of Experiments中生成10个设计点，如表2所示，并对10个设计点进行模拟。

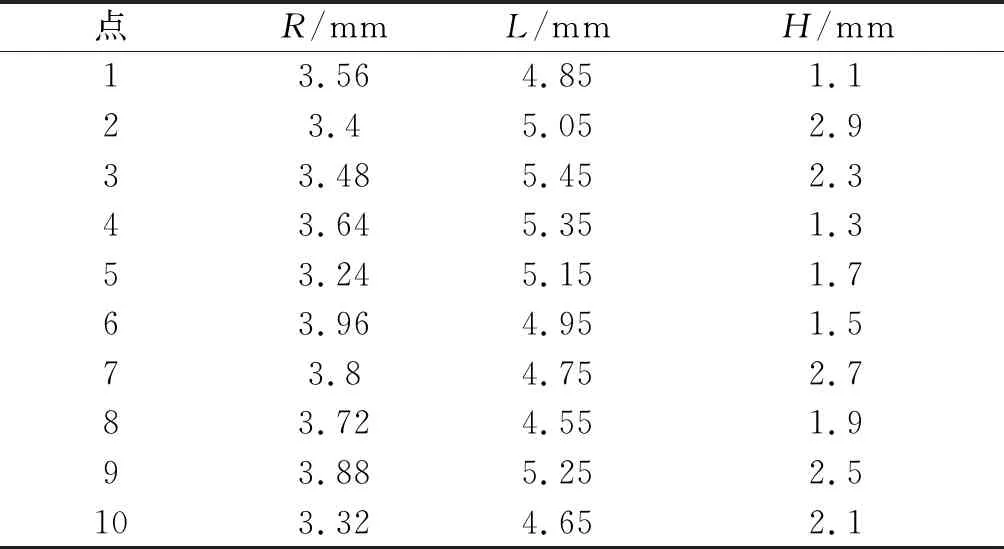
表2 生成的设计点

完成对以上10个设计点的模拟后，就能够得到3个输入参数(最大值和最小值之间)中任意值与其对应的输出参数的一个评估。评价响应的主要方法有以下三种。

1)响应图

2D响应图表示某一个参数与输出参数的变化关系，3D响应图表示任意两个输入参数与输出参数的变化关系。图5为R、L、H分别与熵增的变化关系曲线，图6为参数R、L、H中任意两个参数所对应的熵增变化。

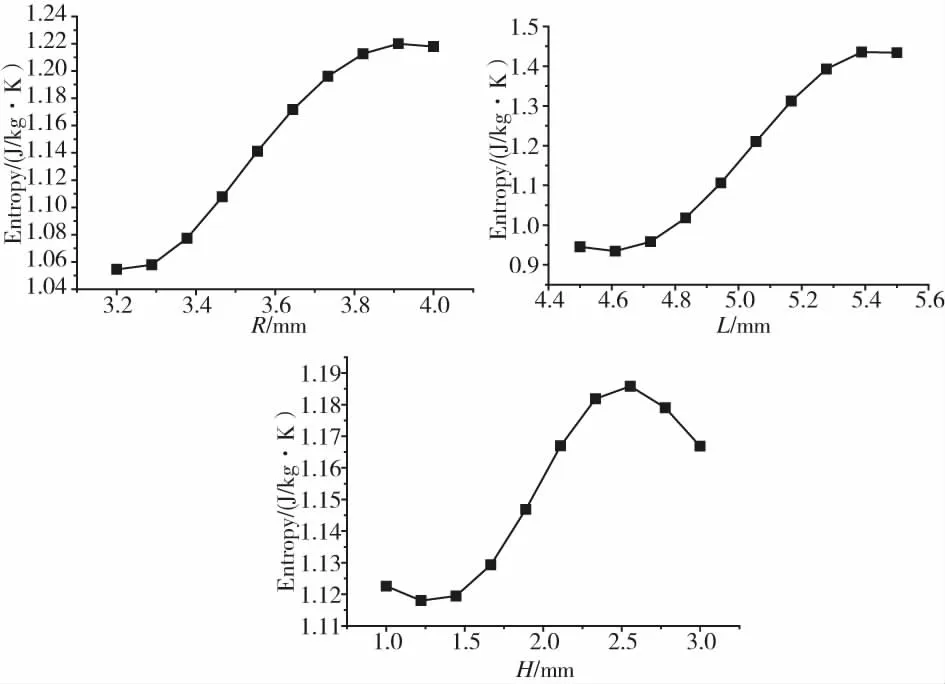
图5 熵增与R、L、H的二维响应

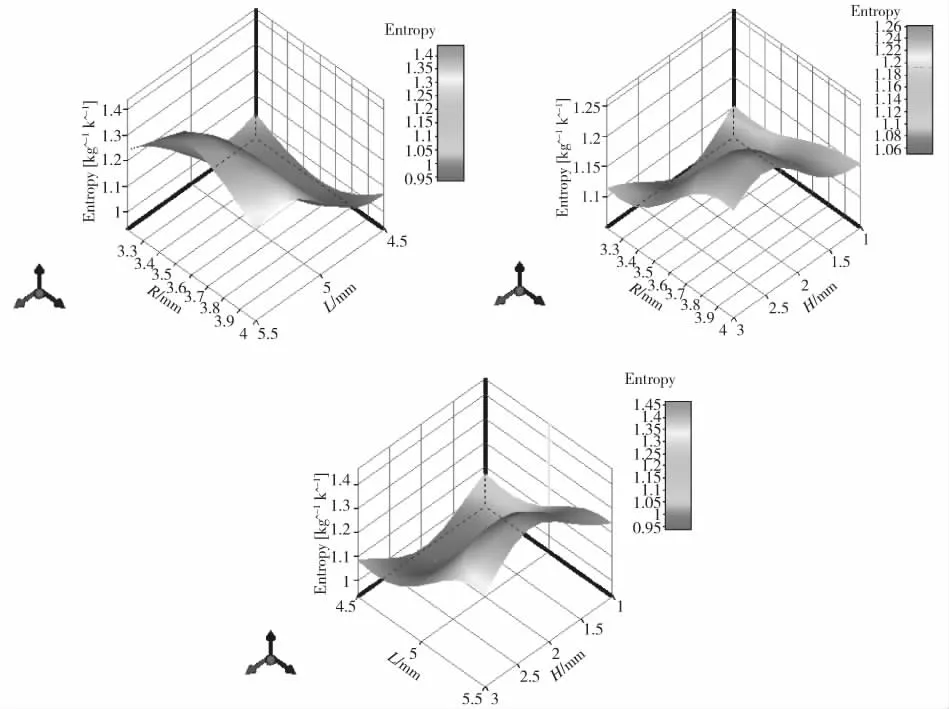
图6 熵增与R、L、H的三维响应图

从图5可以看出，可变参数R、L、H随优化目标熵增的变化情况。输入参数R、L随着尺寸的增大，有一小段熵增呈下降趋势，紧接着随着输入参数尺寸的增加逐渐增大，R在3.9 mm，L在5.4 mm时显示出下降的趋势。H随着尺寸的增大先减小，后逐渐增加，在2.5 mm时有明显的下降趋势。

图6显示了R、L、H两两配合，对熵增的影响变化情况。但基本显示得出一个趋势，大尺寸的配合会产生很大的熵增，同时，小尺寸的配合并非熵增最小。因此，其三者之间的配合应该有最佳值，使得熵增最小，能量损失最小。

2)局部灵敏度(Local sensitivity)

局部灵敏度是通过对比设计变量的变化情况，得出变量对输出参数的灵敏程度。如图7所示，参数R、H对压差的灵敏度为负值，说明该参数对压力无影响，压差主要依赖于L的尺寸大小。R、H、L对熵增灵敏度为正值，因此三个参数对熵增都有影响，且L的尺寸熵增的影响最显著。

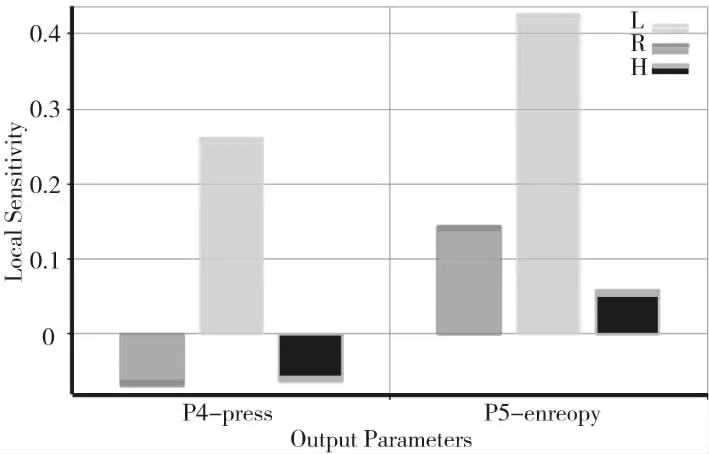
图7 响应点局部灵敏度图

3)蛛状图(Spider chart)

蛛状图是将所有的输出参数和其变化规律在一个简图上表示。

图8 蛛状图

2.2.2 目标驱动优化

通过目标驱动优化工具，可以找到最佳位置的响应曲面。目标驱动优化是一种确定目标、从一组给定的设计点中得到最佳设计点的优化技术。在目标驱动优化设计中，首先设定输入参数和输出参数的变化范围及设计点数目，然后指定设计参数的重要性，生成具有一定数目设计点的样本，最后通过筛选得到一个最佳的设计样本作为最终优化结果。

设置优化目标：

最小化Pressuredrop(压差)并将其重要性设为“Higher”；

最小化Entropy(熵增)并将其重要性设为“Higher”；

将R、H、L的尺寸保持最小。

完成上述设置，在特性中选择“Screening”(筛选)作为20个设计样本的优化处理方式。通过分析计算，最终得到了三个候选设计，并标记了星号等级(星号越多越好)，如图9所示。

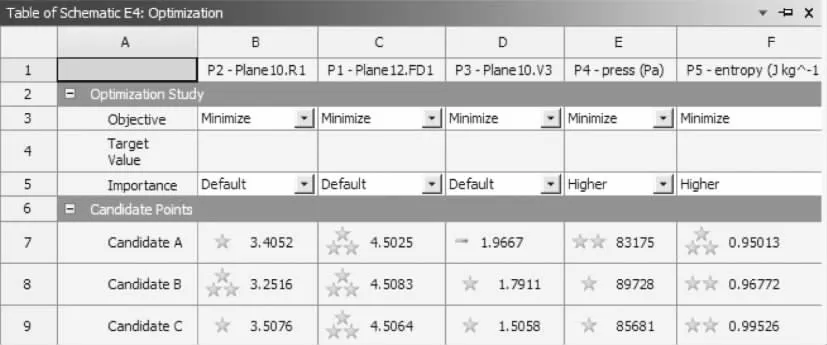
图9 候选设计标记图

在20个样本点中，相比其他候选项，A是本例中的最佳设计样本。平均压降达到了83175 Pa，而最小熵增达到了0.950 J/kg·K。这种情况下的R、L、H分别是3.405 mm，4.502 mm，1.967 mm，即进、出口倒角为35.5°。

权衡图代表了在目标驱动优化中使用的样本组，如图10所示为该目标驱动优化的权衡图。

权衡图中通过不同方块表示与设计目标的匹配程度，深色的表示好，点状的表示差。图形提供了关于输出参数的大量信息，通过图10，很明显，0.077 MPa的压降对应了一个1 J/kg·K的熵增，但是要用一个0.1 MPa压降实现同样的熵增是不可能的。

运用选定的最佳候选输入值，通过Fluent软件完整地模拟该种滑阀运动过程中配气系统的气动力特性，得到最终的结果，与响应面的预测精度进行比较。通过对最佳设计点A进行全面的Fluent计算，给出了更新后的值，它们与响应面得到的预测值有很好的吻合。其中由响应曲面得到的预测值为平均压降Press=0.083 MPa和熵增Entropy=0.950 J/kg·K，而最佳设计点更新后的值为0.0836 MPa和0.929 J/kg·K，两者误差率分别为0.7%和2.21%，两者吻合的非常好。

3 优化后配气系统的数值模拟

3.1 边界条件设定

本文主要研究配气过程中，在不同滑阀开度下，配气系统的气动力特性，即整个过程中的流场、压力场、温度场、速度场和熵增的变化情况。因此，为了准确地研究该变化过程，模型采用了动网格，并采用非稳态求解。模拟中边界条件的基本设置如下：

1)运用Fluent求解器选择非稳态设置，即Transient。由于进气压力高，压力梯度较大，气体流速快，求解器选用适用于高速可压缩流动的耦合隐式求解器，湍流模型采用单方程(Spalart-Allmaras)模型，该模型适用于计算压力梯度较大的气体流动，具有非常好的效果。

2)材料选用可压缩的理想气体，即ideal-gas，其中粘度(Viscosity)设置为Sutherland，即其遵循萨兰德定律。

3)气流进口：采用压力进口边界条件，进口压力为10 MPa，温度300 K。

4)环境条件：压力为标准大气压，温度为300 K，壁面绝热。

5)滑阀及气缸活塞的运动采用动网格(Dynamic Mesh)技术实现。为了满足整体的要求，将Smothing、Layering、Remeshing等合并使用，生成高质量的网格，避免负体积的出现。滑阀和气缸壁的运动采用UDF实现[2]。

3.2 不同开度下的压力云图

将配气滑阀进行优化设计，选取最佳设计点进行全面的数值模拟，得到不同开度下配气系统的压力云图，如图11所示。从压力云图可以看到，整个配气过程比原来流畅，因为腰孔的直通道代替了原来滑阀的导杆，减少了阻力及扰流，同时整个配气系统的压力分布均匀，尤其是气缸中的压力。在滑阀关闭时，气缸内的压力达到9.069 MPa，比优化之前的8.936 MPa提高了1.49%。

3.3 不同开度下的熵增云图

选取最佳设计点进行全面的数值模拟，得到不同开度下配气系统的熵增云图，如图12所示。从图中可以看到，不同开度下的最大熵增比优化前都小。在全开到开度=3.14 mm期间，滑阀内部的熵增非常小，最大时达到0.87 J/kg·K，随着开度的逐渐减小，熵增有所增加，开度越小，熵增越明显，但在近乎关闭时熵增为3.07 J/kg·K，比优化前的7.91 J/kg·K减小了61.2%。

图13为优化前后滑阀内部的熵增，很明显，优化后的滑阀，其内部熵增在不同开度下都比优化前小很多，随着开度的增加，熵增逐渐增大，其增大其实非常明显，这与优化前有很大不同，主要原因是优化前的滑阀内部有导杆，同时节流作用影响较大，但优化前的滑阀内部熵增在开度=1.5 mm后也表现出了同样的趋势。

图11 优化后不同开度下配气系统压力云图

图12 优化后不同开度下配气系统熵增云图

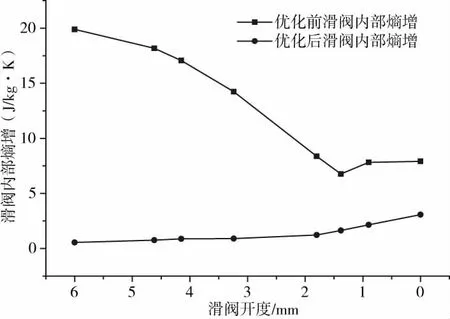
图13 优化前后滑阀内部熵增

3.4 不同开度下的速度矢量图

图14为开度=1.8 mm和开度=0.9 mm两种开度下配气过程的速度矢量图。从图中可以看到，在进口节流处的节流效应没有明显的减弱，出口节流口的节流效应由于倒角的存在，使流体平滑流出，节流得到了减弱，因此整个滑阀的损失减小，达到了优化的目的。

图14 优化后不同开度下配气系统速度矢量图

3.5 配气过程的流量和气缸推力

图15为优化前后不同开度下的进气流量，从图中可以看到，流量的变化趋势都是从最大流量随着开度的不断减小而减小，直至为0。优化前后流量变化的趋势基本一致，优化后的进气流量比优化前的进气流量小。

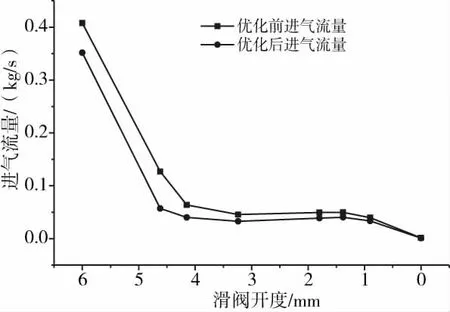
图15 优化前后不同开度下进气流量

图16为优化前后不同开度下气缸的推力，两者趋势基本一致，先逐渐增大，达到最大值，然后随开度减小而减小。很显然，优化后气缸的最大推力达到2009.50 N，推力比优化前大，而且变化平缓，同时由于优化后的流量比优化前小，因此也证明了优化后的气体损失减小，优化取得了一定的效果。

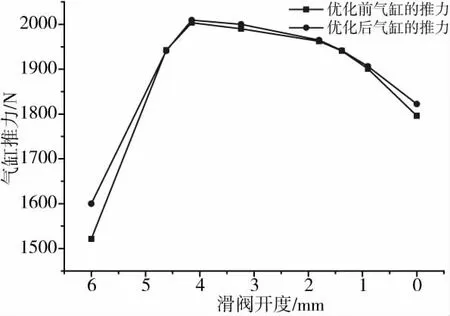
图16 优化前后不同开度下气缸推力

4 小结

1)通过响应曲面优化和目标驱动优化，得到了在配气过程中能量损失最小的配气滑阀的结构和内部尺寸。与优化前相比，进气结束后气缸的压力为8.936 MPa，提高了1.49%，滑阀内部熵增减小了61.2%，最大程度地降低其不可逆损失，提高了配气效率。

2)对于高压气体数值模拟，刚开始压力梯度较大，时间步长要非常小。到一定时间步，为了加快求解速度，将时间步长加大，虽提高了求解速度，在一定程度上影响了模拟的精确性。

3)优化设计中的设计点是Workbench中的优化设计软件选取的，由于其受到计算机硬件和计算时间的影响，选取的设计点不多。在后续研究中可以选取更多的设计点或者运用遗传算法进行优化，增加优化的准确性。