综合多阶段退化和多不确定轴承剩余寿命预测
范乐贤,刘淑杰,张洪潮,2
(1.大连理工大学机械工程学院,辽宁 大连 116024;2.德克萨斯理工大学工业工程系,美国 德克萨斯 卢伯克 79409)
0 引言
滚动轴承是机械设备的关键部件之一,广泛应用于各种设备中,它的退化或失效将直接影响设备的性能和可靠性,这使得尽早检测和预测任何类型的潜在异常和故障并实施实时容错操作以最小化性能降级和避免危险情况成为必要[1]。RUL预测作为预后与健康管理的关键环节,近年来有大量的学者研究。目前主流的RUL预测方法主要有三类:基于物理原理的方法、数据驱动的方法和混合方法[2]。其中,有限的失效机理研究、复杂的物理模型和实时的参数估计方法限制了基于物理原理方法的进一步应用。数据驱动方法可分为两类:人工智能方法和基于退化趋势的方法[2]。前者从大量同类设备的状态监测(condition monitoring,CM)数据中提取深层特征,使用智能算法学习深层特征和使用寿命之间联系,进一步实现RUL预测[3-4]。后者从监测信号中提取健康指标(Health Indicator,HI),根据服役环境、退化过程、专家知识和可用数据对退化趋势进行建模,实现对退化趋势的预测[5-6],预测结果可以表示为随机、概率或确定性变量,近年来基于退化趋势的数据驱动方法在滚动轴承RUL预测中得到了广泛的应用。
随着故障程度的发展,轴承的HI一般呈现出变化的退化趋势,单一的退化模型很难描述随时间变化的退化过程。因此,有必要在RUL预测之前根据趋势变化将退化过程划分为不同阶段并建立对应的退化模型[7]。Lim等使用三个动态模型描述轴承的三种退化过程,并通过贝叶斯算法计算不同模型的概率划分退化阶段[8]。Cui等用三个多项式函数表示轴承的正常、缓慢退化和加速退化,通过设置相对误差阈值和计算状态概率判断退化阶段[9]。Wang等将退化过程分为正常和退化阶段,分别用不同的函数形式描述退化阶段,并用基于3σ区间的检验方法确定退化起始[10]。Ahmad等使用线性和二次动态回归模型描述健康指标的两种趋势,并用警报界限技术确定退化起始点[11]。此外,HI的退化趋势不仅具备多阶段的特点,往往还受制作工艺、服役时间和工况环境等因素的影响,导致每个阶段的退化路径具备不确定性变化,因此对退化路径不确定度进行有效管理同样是广泛关注的问题。Hu等建立了退化速度随运行时间和外部因素变化的线性维纳模型[12]。Lei等建立一种同时考虑退化时变性、个体差异性、非线性可变性和测量可变性四种不确定性源的随机过程模型[13]。Wen等在幂函数模型中引入导致退化路径不确定性的三种因素[14]。Gao等提出一种能够拟合多级线性退化同时考虑个体差异的随机模型[15]。
综合以上基于退化趋势的轴承RUL预测方法,可以发现考虑多阶段退化和趋势不确定性的预测方法是相互独立的。然而,根据轴承的实际退化情况,HI趋势是同时具备多阶段和多种不确定性特征的综合过程,目前还没有将这两种特征结合的预测方法。因此,本文提出一种能够拟合多阶段退化趋势,同时考虑趋势多不确定性的RUL预测方法。
1 退化建模和RUL预测
1.1 退化建模
轴承时域振动信号由随机噪声和周期性波动组成。在振动数据的时域分析中,可以提取具有良好演化趋势的时域特征作为HI,而均方根(Root Mean Square,RMS)是具有良好上升趋势特征的代表,因此本文采用RMS作为HI表示轴承的性能退化。根据文献[7]的分析,轴承在全寿命周期会依次经历健康、缓慢退化和加速退化三个阶段,如图1所示。

图1 滚动轴承的退化过程
因此基于维纳过程采用常数、线性和非线性形式描述三个阶段HI的变化。即:
x(t)=x0+σB(t)
(1)
x(t)=x0+ηt+σB(t)
(2)
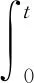
(3)
式中,η是漂移系数,表示轴承的退化率;σ是扩散系数,表示同类轴承的共同特性;x0是每个阶段的初始状态;Λ(t;θ)是非线性退化函数,本文采用幂函数形式Λ(t;θ)=tθ。
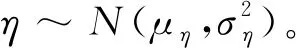
y(t)=x(t)+ε
(4)
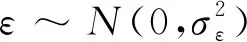
实际中,CM数据通常为离散形式Y1:k={y1,y2,…,yk}。同样地,X1:k={x1,x2,…,xk}表示对应CM数据的退化状态。因此,基于上述多阶段退化过程及不确定性的定义,建立具有三种不确定性的随机退化模型。
常数模型:
(5)
式中,zk=[xk],A=[1],Q~N(0,σ2),H=[1],R~N(0,δ2)。
线性和非线性模型:
(6)

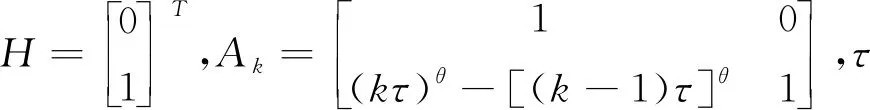
1.2 RUL预测
在工程应用中,将轴承HI首次超过失效阈值的使用时间视为有效寿命是很自然的,则轴承RUL可以看作是当前时间和首达时之间的时间间隔,其中,首达时是随机过程首次达到某值的时刻。根据有效寿命定义和首达时的概念,tk时刻的RULLk表示如下:
Lk=inf{x(l+tk)≥ω|x(tx)<ω}
(7)
则上文提出的退化模型对应的RUL的条件概率密度函数(Probability density function,PDF)为:
(8)
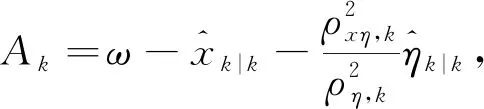
Γk=Π(lk+tk;θ)-Π(tk;θ),Π(t;θ)为HI退化形式。上式详细证明参见文献[18-19],此处省略。然而,利用上述分布在线预测RUL时,不仅需要失效阈值ω,还需要估计状态zk|k的期望、方差以及SSM中的相关参数。
2 自适应参数估计和阶段划分
2.1 参数估计

然后构造参数向量Θ的联合似然函数关于CM数据集Y和状态集Z的条件期望:
[(yi-Hzi|k)(yi-Hzi|k)T]}
(9)
(10)
假设(10)式中

(11)
2.2 阶段划分
SPC是一种利用数理统计控制过程和减少波动的统计技术,可以实现对过程进行及时有效的调整和决策。由于退化过程的不稳定性,CM数据偶尔会出现偏离正常范围的“奇异值”,这种现象会对阶段划分产生一定的干扰,从而导致阶段的错误估计。为了准确识别退化阶段,避免“奇异值”引发阶段错误估计,提出基于SPC的阶段划分方法,通过监测残差变化识别退化阶段。
由于退化时变和测量噪声等不确定性因素的存在,即使在同一阶段内,退化状态和HI也并不保持恒定,而是在一定范围内波动。这里将残差定义为退化状态的期望E(x1:k)和HIY1:k之间的差值,即k=yk-E(xk)。通过对建立的退化模型分析可知,残差k应服从则使用EWMA控制图监测k的动态变化,其上下控制限(Up/Low control limit,UCL/LCL)为:
(12)
式中,K为控制限宽度;λ为EWMA权重;μ为EWMA统计量的均值。
若Ei在控制限内,则认为退化阶段不发生变化是合理的。否则,有理由判断退化阶段发生改变。然而,仅用一个超过控制限的残差进行阶段划分仍然是不准确的。因此,根据统计过程控制的判稳准则,计算不同控制限下的最小采样次数,如表1所示。

表1 不同控制限下满足稳定判据的最小采样次数
3 实例研究
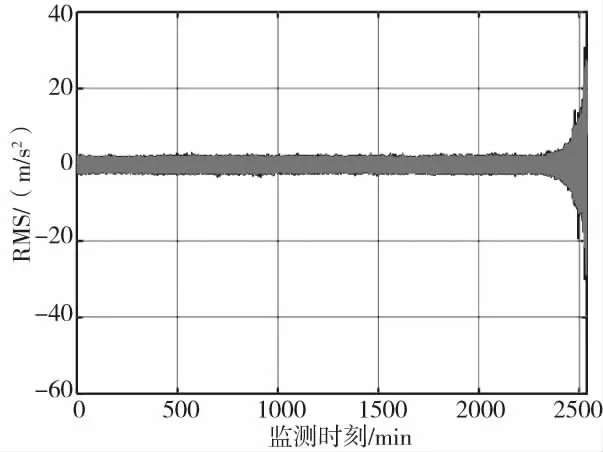
图2 轴承生命周期的振动数据
为了验证该方法的有效性,本节给出一个滚动轴承的实例,CM数据来自XJTU-SY轴承数据集[20]的Bearing3_1。图2显示出了所采集的全寿命振动信号,本文从500min开始对轴承进行状态监测,并使用相对法确定轴承失效阈值[20]。
在整个监测过程中,从CM数据提取的RMS变化如图3中的左小图曲线所示。将提取的RMS带入退化模型估计退化状态,结果如图3所示。图3左侧子图为t=1000~1500min的局部放大图,图3右侧子图为2300min后的局部放大图。从数据的总体趋势来看,前2300min轴承处于健康阶段,估计状态在一定范围内波动,没有明显的退化趋势。2300min后,轴承进入退化阶段,估计状态在2340~2450min间呈现线性退化趋势,在2450min后呈现非线性退化趋势。当轴承运行到2490min时,退化状态首次达到失效阈值,其寿命被认为终止。在500~2490min监测期间共采集1990组CM数据,使用提出的参数估计方法根据这些数据估计不同阶段下的参数向量θ,如图4所示。

图3 基于RMS的状态估计结果
使用提出的参数估计方法在每个CM点获取参数向量θ。为保证模型参数预测精度,待处理数据累积到5组再进行估计,然后每次采样新数据后更新估计结果。不同阶段的估计结果如图4所示,图4(a)、图4(b)、图4(c)分别为健康阶段、缓慢退化阶段和加速退化阶段的结果。从图4(a)、图4(b)可以看出,随着CM数据的积累,模型参数可以快速收敛并保持稳定。在每个阶段结束时(t=2342min和t=2462min),模型参数都发生一定程度的变化,这与相应时刻发生阶段变化的实际情况一致。从图4(c)可以看出,估计参数在一定范围内波动,这也符合加速退化阶段内轴承退化严重、运行状态不稳定的实际情况。这些结果表明了本文提出的参数估计方法具有自适应估计能力。

图4 每个阶段的参数估计过程

图5 阶段划分结果
计算估计状态和RMS的残差,得到每个监测点EWMA统计量Ei,结果如图5实线所示,其中(a)、(b)分别表示健康阶段和退化阶段,虚线为控制限K=3求得的上下控制限。
图5中的统计量Ei大部分在控制限内,少数(小圆圈)发生“越界”,由稳定判据可知上述“越界点”是该阶段内的奇异值,表明建立的模型符合退化阶段的实际情况。但在t=2342min和t=2462min后,短时间内出现大量的“越界点”,相邻“越界点”间的距离不足稳定判据中规定的最小采样次数,此时有充分的理由认为退化阶段发生了变化。将改变点后的监测数据带入相应的随机退化模型中,统计量Ei又恢复到控制限内,说明所建模型又符合变化后的退化情况。上述现象表明,所提阶段划分方法可以有效划分不同阶段的监测数据,并及时确定阶段变化点。

图6 退化阶段估计RUL的PDF
基于上述状态、参数及阶段估计结果,根据(8)式计算退化阶段内各监测点的RUL分布,结果如图6所示。在每个退化阶段初期,由于缺少足够的监测数据,估计参数不确定性较大。因此,PDF曲线多为“扁平”形状,可能的RUL范围较广,但PDF分布仍覆盖了真实的RUL。随着监测数据的积累,特别是在估计参数收敛后,PDF曲线越来越“尖锐”,可能的RUL范围变窄,这表明预测结果的不确定性降低,可以为后续决策提供有效的信息。
以PDF最大值代表各时刻的预测RUL,预测结果如图7所示。可以看出,退化初期CM数据较少,导致估计参数不确定性较大,预测结果误差较大。随着CM数据的不断积累,估计参数逐渐收敛并接近真实值,RUL预测结果也逐渐趋于稳定,预测精度上升。但此时根据CM数据只能判断出轴承具有线性退化趋势,不能预测未来的非线性退化趋势。因此只能预测缓慢退化对应的RUL,如图7(a)虚线所示,导致真实RUL和预测RUL有一定的差别。倘若只考虑轴承缓慢退化,即只考虑轴承线性退化部分,如文献[9]。图8中显示了只考虑轴承线性退化时,文献[9]和本文预测的均方根误差比较。

图7 退化阶段的预测RUL
可以看出,如果只考虑轴承线性退化部分,本文预测的均方根误差与文献[9]相比更小,表明该方法的预测精度比文献[9]有所提高。此时,文献[9]认为轴承失效,而根据“相对法”设定的失效阈值更接近真实失效阈值。因此,本文进一步预测下一个时期的RUL,结果如图7(b)所示。可以看出当轴承进入最后的加速退化阶段,由于退化阶段不再发生变化,根据CM数据预测的退化趋势即是最终趋势,因此预测精度大大提高,预测RUL皆在30%的误差限度内。随着CM数据的积累,模型参数逐渐收敛,RUL预测也进一步靠近真实值。这些结果表明,所提方法在预定失效阈值下,能够预测全寿命周期内的RUL。

图8 只考虑轴承缓慢退化时预测RUL的均方根误差
4 结论
为了描述轴承健康指标的退化趋势同时具有多阶段变化和多不确定性的特点,本文提出一种新的随机退化模型,该模型同时考虑个体差异性、退化时变性、测量可变性和多阶段退化。为了准确划分退化阶段,提出一种基于EWMA控制图的阶段划分方法,用于自适应切换退化模型。同时,在缺少同类轴承先验信息的情况下利用基于EM算法的参数估计方法在线更新模型参数。最后,通过对仿真数据和XJTU-SY数据集的实证研究,验证该方法的有效性。结果表明,该方法能够准确划分滚动轴承的不同阶段,并根据监测数据提供不同退化阶段的RUL预测。

