基于等离子体合成射流的后台阶流动控制*
王泽阳,王建明,王怡菲
(沈阳航空航天大学 航空发动机学院 辽宁省航空推进系统先进测试技术重点实验室,辽宁 沈阳 110136)
0 引言
后台阶流动(backward-facing step,BFS)为一种具有简单几何外形却有着复杂流动机理的分离流动,其作为突扩截面流动的典型代表,广泛的出现在流体工程领域中。这种流动分离存在会产生流动损失,引发噪声与振动等问题。因此研究对后台阶流动分离的控制具有重要的应用价值。
主动流动控制作为一种新型的流动控制方式,具有适用工况宽、应用灵活等优势,吸引了许多学者的关注,可以将其应用于后台阶流动控制中。Mehrez等在台阶分离点引入正弦振荡射流,通过对流场产生振荡激励使得主流再附点位置得到提前[1]。Emami-Naeinie等采用在台阶垂直壁面上吸气或吹气的方式,提前或推迟了主流再附点的位置[2]。Abu-Nada等在台阶下游施加吸气或吹气的控制方式,实现了对再附点的提前和推迟[3]。Sano等采用在台阶下游水平壁面上开设小孔在分离区吸气的方式,实现了对再附点位置的提前[4]。Uruba等采用在台阶垂直壁面下部开设小孔产生吸气或吹气的方式对再附点的位置进行控制,结果表明吸气或吹气均能将再附点的位置提前[5]。
合成射流是一种新型的主动流动方式,无需额外的气源供应系统,能够产生零质量射流,具有结构简单的优点,被广泛应用于流动控制之中[6]。李斌斌等将合成射流激励器设置在后台阶分离点前缘,通过合成射流的吹吸作用将再附点的位置提前[7]。Hsu等将合成射流激励器设置在台阶垂直壁面的上部,减小了主流再附长度[8]。介质阻挡放电(dielectric barrier discharge,DBD)等离子体激励器是一种新型主动流动控制装置,由于等离子体激励器不存在机械活动部件,故有着不会增加系统的复杂性的优点,近年来在流动控制领域得到了广泛的应用[9]。Boom等[10]和赖晨光等[11]将等离子体激励器设置在台阶分离点前缘,通过等离子体激励器的壁面射流作用为边界层注入动量,减小了分离区的长度。王靖宇等将等离子体激励器设置在台阶下游水平壁面,减小了主流的再附长度[12]。目前还未见有通过DBD等离子体激励器构成合成射流,并将其应用于后台阶流动控制中的报道。本文采用Shyy等提出的等离子体唯象模型[13],通过将等离子体激励器布置在台阶竖直壁面上的方腔中,构成合成射流,通过合成射流的吹吸作用,实现对后台阶流动的控制。
1 等离子体模型
本文采用Shyy等提出的等离子体唯象模型[13],将等离子体的作用以体积力的形式添加到动量方程中求解。如图1所示,模型假设电场存在于由电极形成的三角形区域中,且电场强度随着与电极距离的减小呈线性增大趋势。空间中的电场强度可以表示为:
|E|=E0-k1-k2
(1)

图1 等离子体作用示意图
式中,E0=U0/d为O点电场强度,U0为O点电压,d为两电极水平距离,系数k1与k2可以根据临界电场强度Eb计算得到:
(2)
式中,a为等离子体电场作用区域的高度,b为等离子体电场作用区域的宽度,电场强度的分量可以表示为:
(3)
由此,等离子体激励产生的体积力可以表示为:
Fx=ϑρcecΔtEx
(4)
Fy=ϑρcecΔtEy
(5)

图2 计算得到的截面速度型与文献[13]对比
式中,ϑ为激励频率,ρc为电子数密度,ec为电子电荷常数,Δt为等离子体放电时间。本文等离子体激励电压设置为4 kV,激励频率设置为为3 kHz,放电时间为67 μs。参考文献[14]的算例对建立的唯象模型进行验证,得到的流场截面速度型如图2所示,计算得到的速度型分布与文献[13]一致,说明本文等离子体模型设置正确。
2 后台阶流动控制模型与验证
图3为后台阶流动结构示意图,坐标原点位于台阶上端点,产生合成射流的方腔设置在台阶壁面上。参照文献[5],计算域上游高度H为0.25 m,台阶高度h为0.025 m,台阶上游和下游的流向长度分别为6 h和20 h,进口流向速度为5 m/s,基于台阶高度的雷诺数为8559。计算域网格及局部放大如图4所示,射流方腔处网格做加密处理,第一层网格高度为1×10-5m,网格增长率为1.3,整体二维网格数量约为25万。计算采用剪切应力模型(SSTk-ω)定常求解,边界条件参考文献[5]进行设置,入口湍流强度为0.1%,水力直径为0.143 m,出口为压力出口,壁面为无滑移绝热壁面。
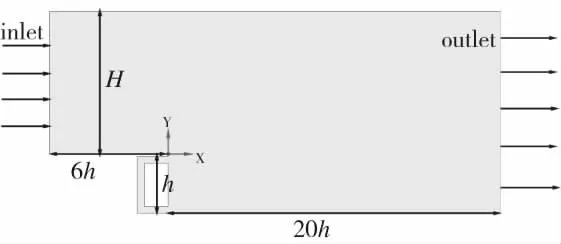
图3 后台阶流动结构示意图
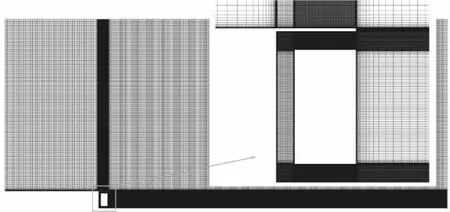
图4 计算域网格及局部加密
图5为后台阶等离子体合成射流的结构尺寸图,方腔开口宽度为3 mm,流向深度为10 mm,垂直方向高度为18.5 mm,根据方腔内部等离子体激励器的布置位置可以分为四类工况:将等离子体设置在方腔下部,体积力方向由右向左(图5(a));将等离子体设置在方腔上部,体积力方向由左向右(图5(b));将等离子体设置在方腔下部,体积力方向由左向右(图5(c));将等离子体设置在方腔上部,体积力方向由右向左(图5(d))。根据施加的激励强度不同可以分为三类工况:激励电压3 kV激励频率2 kHz,激励电压4 kV激励频率3 kHz和激励电压5 kV激励频率6 kHz。

图5 后台阶等离子体作用区域结构示意图

图6 基态速度场
为验证数值模拟的正确性,参照文献[5],对未采用等离子体合成射流控制的基态流场进行数值模拟,基态工况下后台阶流动速度场如图6所示,上游边界层在台阶后分离,形成由一个顺时针旋转的主涡和一个逆时针旋转的小的角涡组成的分离区,主涡涡心位于X/h=2.65处,主流在分离区后再附于下游壁面,形成新的边界层,根据再附点的壁面剪切力为零可以确定再附点位置xr/h为5.749,对比文献[5]实验测得的xr/h=5.625,误差为2.2%,说明模拟方式合理可靠。
3 后台阶流动控制的结果与分析
3.1 流场结构的结果与分析
图7(a)、(c)、(e)为将等离子体设置在方腔下部,体积力方向由右向左工况下(图5(a))的流动速度场结构图,图7(b)、(d)、(f)为将等离子体设置在方腔上部,体积力方向由左向右工况下(图5(b))的流动速度场结构图,这几种工况能够使方腔在下部开口吸气,在上部开口吹气。对比基态流场,可以发现在等离子体合成射流的吸气作用下,分离区的角涡在抽吸作用下消失不见,分离区主涡涡心位置向上游移动,这使得分离区面积减小。射流的吹气作用为分离的主流注入了动量,这加快了主流的再附。随着激励电压和激励频率的增加,等离子体合成射流的强度变强,对后台阶分离的控制效果也得到加强,再附点的位置也得到提前。
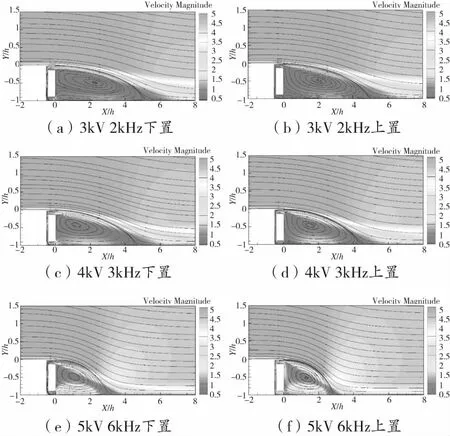
图7 各吸气工况下的后台阶流动速度场
图8(a)、(c)、(e)为将等离子体设置在方腔下部,体积力方向由左向右工况下(图5(c))的流动速度场结构图,图8(b)、(d)、(f)为将等离子体设置在方腔上部,体积力方向由右向左工况下(图5(d))的流动速度场结构图,这几种工况能够使方腔在下部开口吹气,在上部开口吸气。对比基态流场,可以发现下部开口吹气的射流作用将主涡冲击破坏为多个小涡,在Coanda效应作用下射流与主流交汇,这为分离后的主流注入了动量,加速了主流的再附,上部开口通过吸气效应将分离区内的气体吸入,这有助于减小分离区的面积,使再附点位置得到提前。与吸气工况相似的是,随着激励电压和激励频率的提高,等离子体合成射流的强度得到提高,再附位置得到提前。
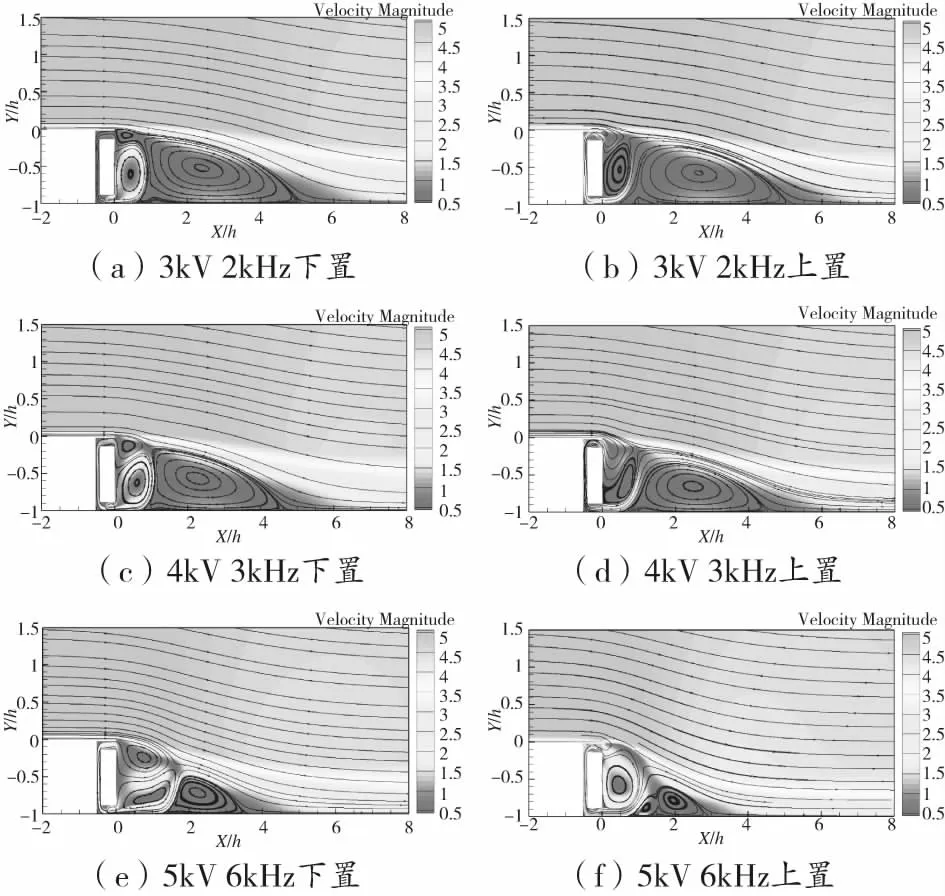
图8 各吹气工况下的后台阶流动速度场
3.2 下游壁面剪切力分析
图9显示了各工况下游壁面剪切力。图9(a)、(b)表明当在方腔下部开口为吸气状态时,气流流向与主流方向相反,这在开口附近产生了负值的壁面剪切力,随着激励强度的提高,吸气效果得到提高,剪切力的绝对值变大,主流再附点的位置也得到提前,在X/h>10处,控制工况壁面剪切力与基态工况的壁面剪切力基本一致,达到一个渐进值。图9(c)、(d)表明在方腔下部开口为吹气状态时,由于射流作用,在开口附近形成了正值的壁面剪切力,随着激励强度提高,射流强度得到增强,造成的剪切力的绝对值变大,分离区的长度也逐渐减小,与吸气工况相似,在X/h>10处,控制工况的壁面剪切力分布与基态工况基本一致,达到基态工况下的渐进值。根据各工况下的壁面剪切力分布可以确定主流再附点的位置,如表1所示。
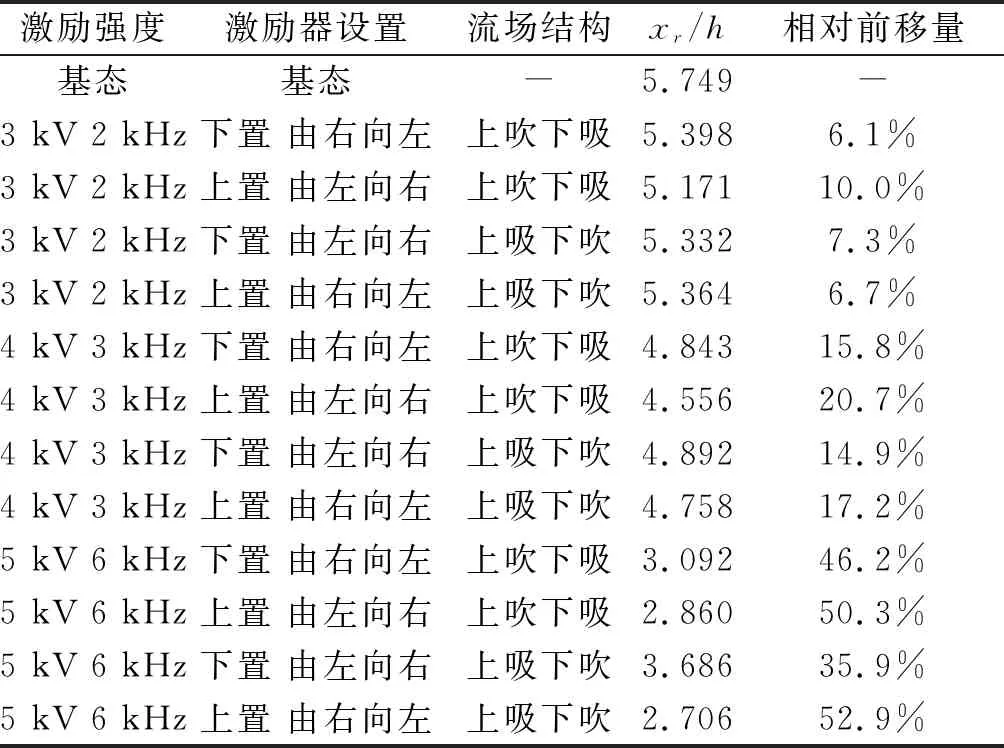
表1 各控制工况下再附点位置

图9 各工况壁面剪切力分布
图10显示了激励器布置方式对壁面剪切力的影响,可以发现将等离子体布置在方腔上部产生的控制效果相对较好。对于3 kV 2 kHz和4 kV 3 kHz两类工况,各类布置方式的控制效果相近,将体积力方向设置为由左向右(见图5(b))使得方腔下部吸气,上部吹气的控制效果相对更佳,相对基态工况分别将再附点前移了10.0%和20.7%。5 kV 6 kHz工况下布置方式的不同对控制效果的影响较为明显,将体积力设置为由右向左(见图5(d))使得方腔下部吹气,上部吸气是最佳的控制方案,相对基态工况将再附点前移了52.9%。

图10 激励器布置方式对壁面剪切力的影响
4 结论
本文采用等离子体唯象模型, 将等离子体激励效果以体积力的形式添加到流场动量方程中,通过在后台阶壁面设置方腔形成等离子体合成射流,实现对后台阶流动的控制,得到主要结论如下:
1)各种等离子体布置方式均能对后台阶流动形成有效控制,将等离子体布置在方腔上部控制效果较好,随着等离子体激励效果的增强控制效果增强。
2)当激励电压为5 kV,激励频率为6 kHz,将等离子体上置,体积力方向设置为由右向左使得方腔下部开口产生吹气效果,上部产生吸气效果时控制效果最佳,相对基态工况可将再附点前移52.9%。
3)等离子体合成射流能够对后台阶流动进行控制的机理为:合成射流的吸气效应能够将分离区气体吸入,减小分离区的长度,吹气作用为分离的主流注入动量,促进了主流的再附。

