对“椭圆中由两垂直直线引出的‘包络’”再研究
2023-01-16 02:25江苏省南通市海门证大中学226100周雅俊
中学数学研究(江西) 2023年2期
江苏省南通市海门证大中学 (226100) 周雅俊

引理1 如图1,在平面直角坐标系中,两定点F1(-c,0),F2(c,0)(c>0,c为常数),点P是以F2为圆心,2a(a>c,a为常数)为半径的圆上的一点,线段PF1的垂直平分线l与线段PF2的交点为点M,则点M的轨迹是以F1,F2为焦点,长轴长为2a的椭圆,且直线l与椭圆相切于点M.
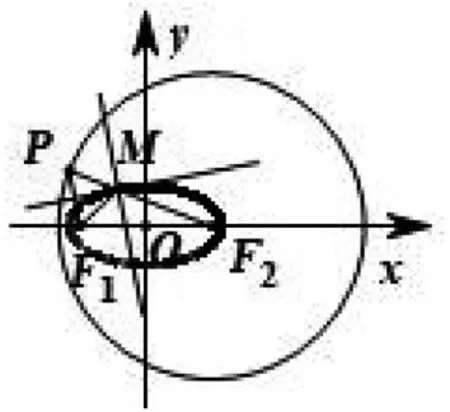
图1
证明:因为点M在线段PF1的垂直平分线l上,所以MP=MF1,那么MF1+MF2=MP+MF2=PF2=2a,又a>c,所以点M在以F1,F2为焦点,长轴长为2a的椭圆上.从运动的角度来看,当点P跑遍圆F2上的所有点时,点M的轨迹就是该椭圆.
下面证明直线l与椭圆相切于点M.设点N是直线l上异于点M的一点,由三角形两边之和大于第三边可以得到NF1+NF2=NP+NF2>PF2=2a,所以直线l上只有点M在椭圆上,其余的点都在椭圆外,所以直线l与椭圆相切于点M.
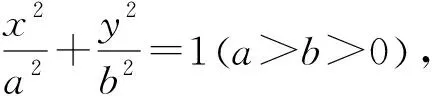

图2




所以当直线PQ的斜率存在时,点N在以A为圆心,r0为半径的圆上.从运动的角度来看,当点P跑遍椭圆上的所有点时,点N的轨迹就是以点A为圆心,r0为半径的圆.
在引理2的基础上可以得到引理3.
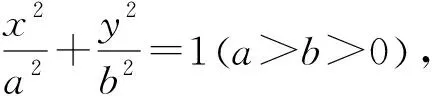

图3
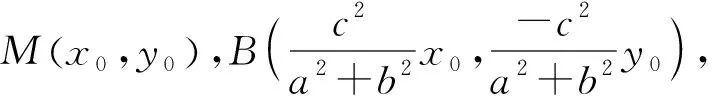
猜你喜欢
小资CHIC!ELEGANCE(2022年1期)2022-01-11
装备维修技术(2022年3期)2021-12-06
中学数学研究(广东)(2021年19期)2021-11-19
中学数学研究(江西)(2019年12期)2020-01-10
中等数学(2018年1期)2018-08-01
南方周末(2018-03-08)2018-03-08
科学中国人(2017年22期)2018-01-02
摄影之友(2016年8期)2016-05-14
数学教学通讯·初中版(2014年1期)2014-02-14
数学大世界·初中生辅导版(2010年2期)2010-03-08

