以问题为核心 促进深度学习*——对一道向量运算题的多角度分析

广东省清远市佛冈县第一中学 (511600) 陈晋城

向量是描述客观世界规律的重要数学模型，它的应用促进了复数、三角函数、几何等问题的解决，它在高考中可以单独命题也可以渗透于三角或者立体几何中，地位不容忽视.本文以笔者在高三复习课中遇到的一道高考模拟题为例，通过多角度、多层次的分析问题，解决问题的深度学习过程，希望能给给读者带来一些启示.

1 题目呈现

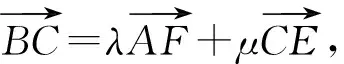
本题是广东省肇庆市2021届高中毕业班第三次统一检测试题第6题.题目以等腰直角三角形为载体提供了一个关于向量运算的数学思维情境，主要考察学生分析、推理、运算、抽象、数形结合等关键能力，通过对本题的深度学习，可以使学生的数学抽象、逻辑推理、直观想象、数学运算等数学核心素养得到提升.

2 解法探究

角度1：坐标法

分析：因为问题是以等腰直角三角形为载体设计的，另外涉及的两个点分别是直角边和斜边的中点，可以很容易建立平面直角坐标系并写出相关向量的坐标.

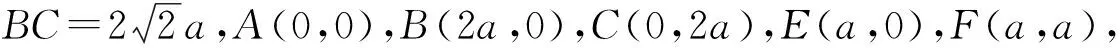
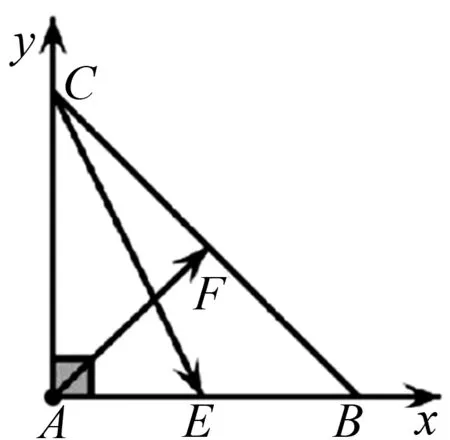
图1

评注：运用坐标法解决向量问题，最关键的是利用“直角”建系，但这个“直角”有时是隐含的，有时需要重新新构造.

角度2 平面向量基本定理

分析:观察本题图像特征及问题呈现，依据平面向量的基本定理，可以选定一个合适的基底，则等式中的所有向量都可以用基底唯一表示出来.因为基底不是唯一的，所以选择不同的基底，同一个向量则有不同的表示方式，但是等式中的参数结果不会改变.

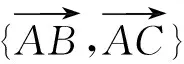
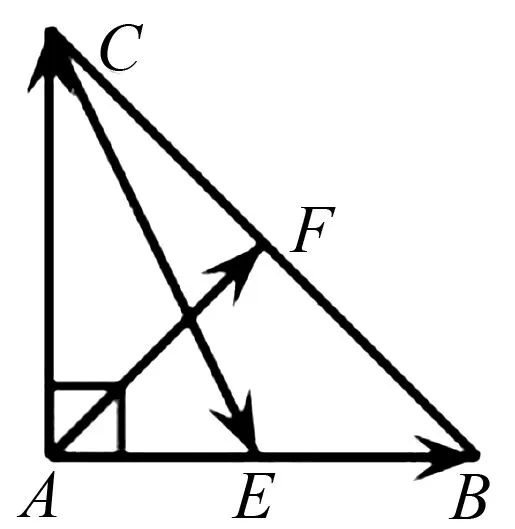
图2

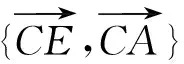
评注：运用平面向量基本定理的过程中，选择不同的基底最，则转化的过程、难易不同.老师要鼓励学生大胆尝试；引导学生重视图像的分析功能；培养学生数形结合的良好习惯.

角度3：平面向量加法减运算法则

分析：确定一个基底，就相当于向量的转化有了目标，而实现这个目标的手段就是平面向量加减法的三角形法则或平行四边形法则.

图3

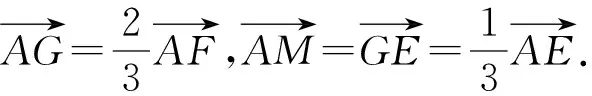
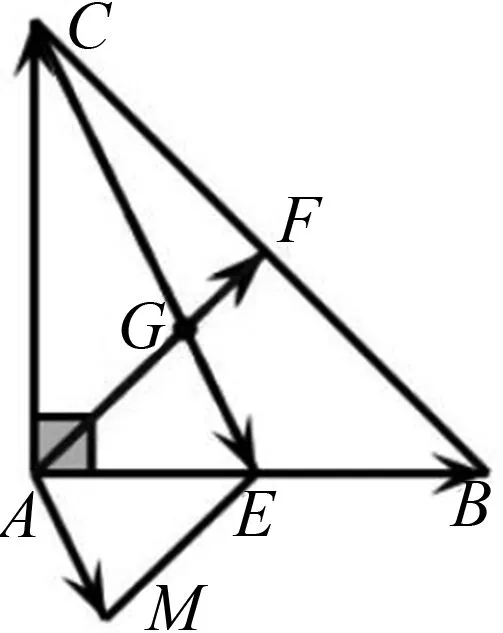
图4

评注：利用图像把题中向量间的直观呈现出来，通过平移、转化等把等式中的向量及与之关联的向量转移到同一个三角形或者平行四边形上去，达到三角形法则或者平行四边形法则的使用条件，体现了化归、转化的思想，数形结合的思想也表现得淋漓尽致.

角度4 方程思想

分析：解二元一次方程组时，常法是代入消元法和加减消元法，把方程组转化为一元一次方程求解，这当中最重要的一步是“消元”.类比解二元一次方程组的解法，可以把λ、μ看成是两个“元”，只要能消去一个“元”就可以得到只有一个“元”的等式进而得解.

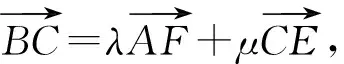
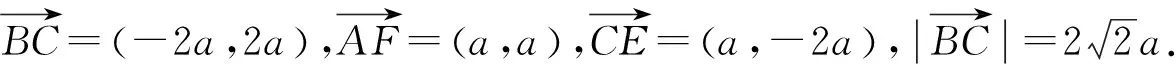
评注：在解法6的基础上，把坐标运算渗透其中，使转化过程量和计算量都降下来，达到了一个事半功倍的效果，避免“小题大做”.因为有“直角”，所以联想到运用“互相垂直的两个非零向量的数量积等于零”以达到消元的目的.但也提出了一个问题：利用方程的思维方法求解类似问题时，如果条件中没有“直角”，那要怎么消元？

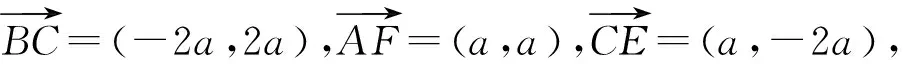
评注：对解法6、7进一步分析发现，若构造与已知向量“垂直的”、“好用(算)的”向量，则可以不受题目条件是否有包含“垂直”这一条件的影响.我们常说做数学题“有条件要用，没有条件创造条件也要用”，正是在解法6、7方法的基础上不断改进，发现可以“创造”特殊向量作为消元的“催化剂”.这是数形结合、坐标法、方程思维等综合运用的成果.

4 反思总结

数学解题必须进行有根据的运算和合逻辑的判断，体现数学的求实精神与怀疑的态度，数学解题常常进行“尝试、猜想、辨析”等探索步骤，又体现数学的探索性和创造性.这一切都要求学生以充分的论据去评判事物的真伪，把握事物的内在规律，提高发现事实和反驳谬误的能力，贯穿一种相信自我、理性分析、缜密推理、求实创新的严谨态度[1].

向量的坐标运算、线性运算、数量积运算都是向量的基本运算，是研究三角、立体几何、复数等的有效方式方法，也是研究物理学、工程学等学科的重要理论工具，因此，我们在教学中必须要能足够重视它.同时，向量运算要求学生熟悉相应的数学情境，了解运算的对象，能够分析已有条件与问题之间的联系，能够分析问题的特征与呈现的形式，提出运算方案，并形成恰当的思维模式，这是数学抽象、逻辑推理、数学运算等核心素养的本质所在，是当下学生需要提升的能力.因此，向量运算提升核心素养方面的非常好的载体.

本案例中，基于向量的特征，向量运算的学习、研究过程需要学习者在完整而深刻地理解相关数学知识的基础上，全身心的投入、积极探究与建构、理解与批判，并有效迁移与运用已有学科知识及思维方法.如运用方程思维解答本题时，解法6用解方程的思维解答本题，其复杂程度远超坐标法等，解法7将解法6进行改进，把坐标法渗透其中，使思维量、转化过程、计算量都降下来.解法8则创造了“有条件要用”，没有条件创造条件也要用”的解题思想，通过构造特殊的“好用(算)的”非零向量使向量运算特殊化.纵观整个学习过程，进行了“尝试、猜想、辨析、改进”等探索步骤，又体现数学的探索性和创造性.实现深度学习的目的.