具有多稳态和可调数目吸引子共存的混沌系统

颜闽秀, 谢俊红, 张 帅

(1. 沈阳化工大学 信息工程学院, 辽宁 沈阳 110142; 2. 工业环境-资源协同控制与优化技术辽宁省高校重点实验室, 辽宁 沈阳 110142; 3. 东北大学 信息科学与工程学院, 辽宁 沈阳 110004)

如今,受到Lorenz混沌系统的启发,混沌已成为研究的热点,许多不同的混沌系统相继被提出[1-6].生成新混沌系统有两个有趣的方向，一种是在简单的数学模型中发现非线性系统中的混沌;另一种是构造具有特殊奇异吸引子的混沌系统,如多涡卷吸引子、共存吸引子等[8-11].平衡点的个数在一定程度上决定了动力学性质.一个经典的理论是一个同宿轨道连接的鞍焦点或两个异宿轨道连接的鞍焦点的系统能够产生马蹄意义下的混沌系统[12].没有平衡点的混沌系统能够产生隐藏吸引子.大量的研究表明,具有多个不稳定平衡点的混沌系统往往具有更丰富的动力学行为，且更容易产生共存吸引子.因此许多学者倾向于构造混沌系统,并通过平衡点的类型来区分动力学特性,如鞍点、不稳定焦点、中心平衡点和其他类型平衡点的混沌系统[13-16].

最近,在混沌系统中吸引子的共存和多稳态性引起了学者们的广泛关注.Li等[17-21]通过数值实验研究了Lorenz混沌系统中的吸引子的共存,并提出了产生共存吸引子的方法.Kengne等[22]提出了Jerk系统中吸引子的共存.Lai等[23-24]介绍了构造具有无穷多奇异吸引子的混沌系统的有效方法.Bao等[25-26]发现,基于忆阻器的混沌系统可以产生不同类型的共存吸引子.多稳态是指两个或多个吸引子在不同的初始条件下共存,具有相同的参数[27]，通常可以在许多非线性动力系统中发现.Ab等[28]发现了具有多稳态和隐藏吸引子的混沌系统;Kengne等[29]提出了一种新型的Jerk混沌系统，并在该系统中发现了五个平衡点、多稳态性和多涡卷.

众所周知,在混沌系统中,具有多稳态和吸引子共存的混沌系统会导致非常复杂的动态行为,应用在工程中有很大的潜力,提出新的具有多稳态和吸引子共存的混沌系统是有意义的.因此，从建立具有简单系统和复杂行为的角度出发,提出了一个具有多稳态的吸引子共存的混沌系统,且将双曲正切函数引入该系统,建立了可调数目的吸引子共存.对该系统的动态特性进行了必要的理论和实验研究，表明该系统能够生成无限多个吸引子的共存并存在多稳态性.最后,基于模型系统进行了模拟电路的实验和验证，表明了该系统能够实现的可能性.

1 混沌系统模型及分析

在经典混沌系统的基础上作考察后[30],描述了一个三维混沌系统，其模型较为简单,如下式所示：

(1)

式中:x1、x2、x3为状态变量；a、b、c、d为系统的常数.将初值取为(0.1,0.1,0.1),图1～3展示了系统(1)的吸引子.

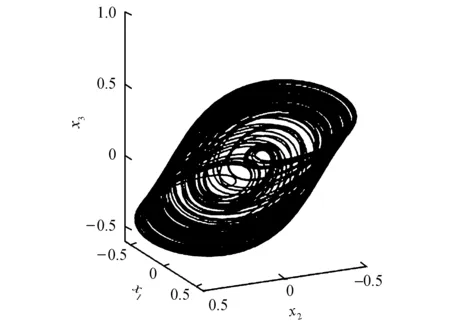
图1 系统(1)三维相图Fig.1 System (1) three-dimensional phase diagram

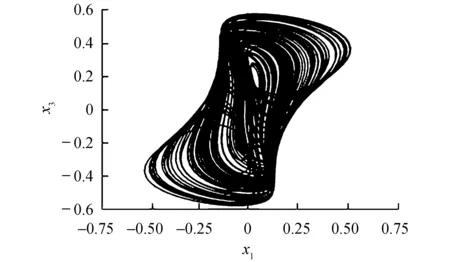
图2 x1-x3相图Fig.2 x1-x3 phase diagram

图3 x2-x3相图Fig.3 x2-x3 phase diagram

当参数a=0.7,b=1,c=1,d=0.5时,系统为三维耗散混沌系统.通过MATLAB计算出系统(1)的李雅普诺夫指数为L1=0.36,L2=0,L3=-0.48.

计算李雅普诺夫维数得到：

(2)

通过李雅普诺夫指数图可看出,系统(1)有正、零、负的李雅普诺夫指数且之和总是为负数,式(2)可看出系统为分数维,因此系统(1)是混沌系统.其中j是满足下式的最大整数：

(3)

通过MATLAB计算出系统(1)的3个平衡点为：A(0,0,0),B(-0.464 1,0.232,-0.464 1),C(0.464 1,-0.232,0.464 1)．

令det(J1-λE)=0,计算其相应特征值．当平衡点为A(0,0,0)时,特征值为(-0.68,0.25+0.968 2i,0.25-0.968 2i)；当平衡点为B(-0.464 1,0.232,-0.464 1)和C(0.464 1,-0.232,0.464 1)时,特征值均为(0.570 7,-0.375 3+1.532i,-0.375 3-1.532i).其中i为虚数单位.

通过平衡点及特征值可以看出,系统(1)有3个平衡点,相对应的特征值有一个实数和两个共轭复数,因此该平衡点为不稳定鞍焦平衡点，且符合混沌系统的指标为2的鞍焦平衡点的条件.因此该混沌系统更容易产生吸引子共存的现象.

综上,对系统(1)进行了一定的理论分析.验证了系统(1)的复杂动力学特性.

2 混沌系统的多稳态性

基于系统(1),选择以初值为(0.1,0.1,0.1)和(-0.1,-0.1,-0.1)进行多稳态分析.图4展示了两组不同初始值下的系统动态演变.

观察图4,发现在两组不同的初始值下系统(1)均存在混沌和周期状态.进一步分析图4a可知,系统在两组不同初始值下存在吸引子的共存且在参数固定状态下呈现出不同类型的吸引子共存.这种具有多稳态的系统其动力学行为更为复杂,即存在共存的周期吸引子和共存的混沌吸引子.图5给出了系统(1)的周期共存吸引子和混沌共存吸引子.

图4 系统动态演化Fig.4 System dynamic evolution

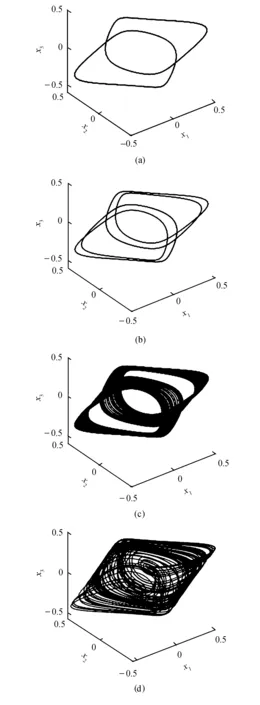
图5 吸引子共存Fig.5 Coexistence of attractors

图5a为周期1共存吸引子,图5b为周期2共存吸引子,图5c和图5d为混沌共存吸引子.显然,通过图5可以看出,当选择固定参数为a=1.1,a=0.95,a=0.88和a=0.7,且初值为(0.1,0.1,0.1)和(-0.1,-0.1,-0.1)时,系统(1)表现出多稳态性,即具有两个吸引子共存的现象.

3 可调数目的混沌吸引子共存

基于系统(1),考虑a=0.7,b=1,c=1,d=0.5,建立双曲正切函数的序列用于生成可调数目的吸引子共存.建立的函数如下式所示：

(4)

其中：n为非负整数；参数β可调节,此时取β=100.可以看出,随着n增大,函数Hi(xi)的零点得到扩展.利用H1(x1)取代系统(1)中等式右边的x1,那么在特定参数下,得到的新系统将会沿x1的方向产生共存吸引子.

首先,考虑沿x1轴的方向产生共存的吸引子,利用H1(x1)取代系统(1)中等式右边的x1,得到如下系统：

(5)

分别取参数n=0,1,2,沿x1轴方向产生的共存混沌吸引子如图6所示.

图6展示了当n=0,n=1和n=2时的混沌共存吸引子.图6a中的混沌共存吸引子对应的初值为(2i-3,0.1,-0.1),其中i=1,2;图6b中的混沌共存吸引子对应的初值为(2i-5,0.1,-0.1),其中i=1,2,3,4;图6c中的混沌共存吸引子对应的初值为(2i-7,0.1,-0.1), 其中i=1,2,3,4,5,6.这些混沌吸引子的共存形状相似,但是轨迹并不相同.若继续增大n的值,系统将会沿x1轴方向产生更多的混沌吸引子共存.

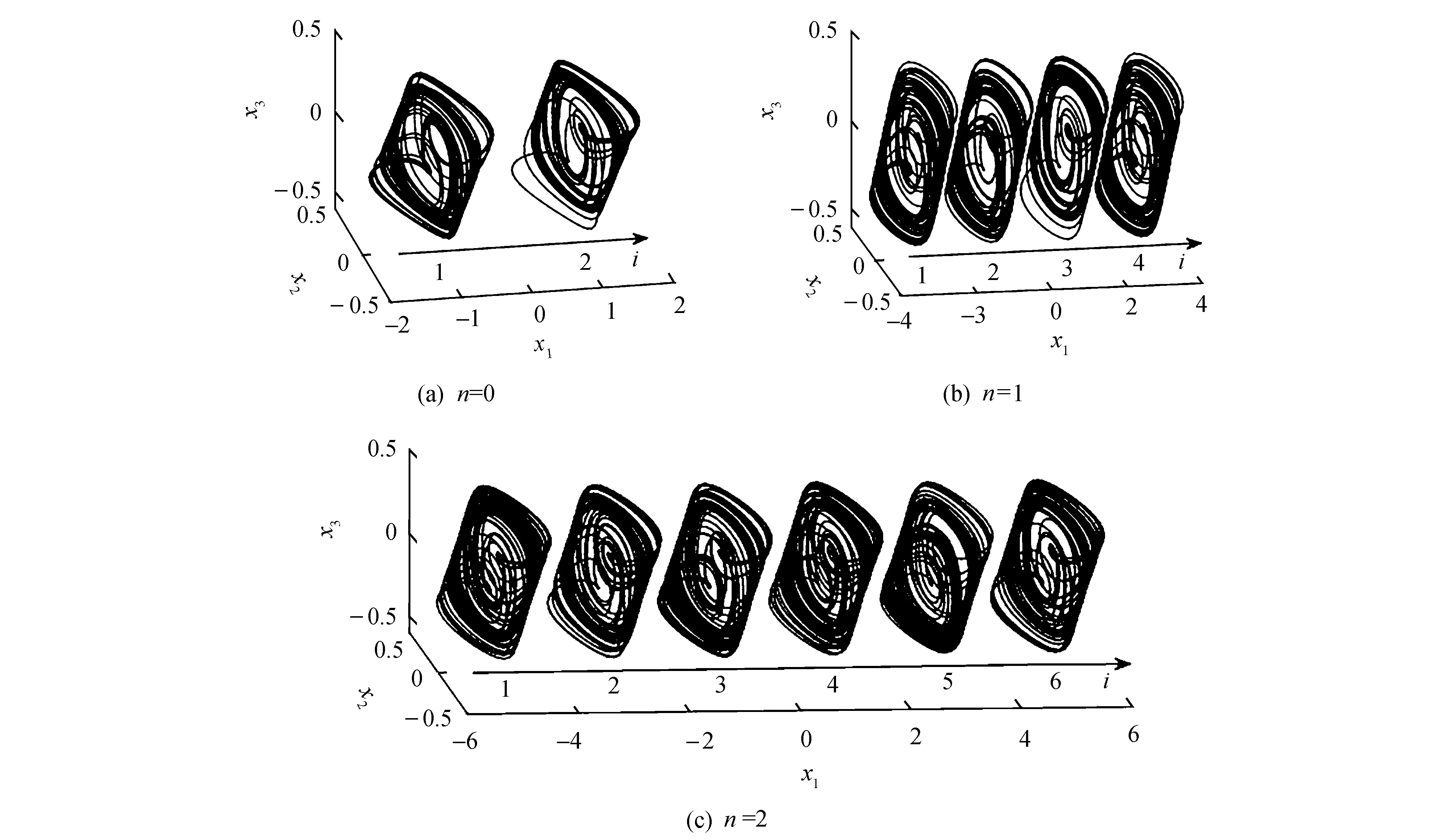
图6 混沌吸引子共存Fig.6 Coexistence of attractors

其次,考虑用H2(x2)取代系统(5)中等式右边的x2,得到如下系统：

(6)

系统(6)将会沿x1和x2轴方向产生共存的混沌吸引子,图7分别给出了参数n为0、1、2时的吸引子.

图7分别展示了2×2、4×4、6×6的吸引子,这些吸引子对应的初始条件分别为(2i1-3,2j1-3,-0.1),(2i2-5,2j2-5,-0.1),(2i3-7,2j3-7,-0.1).其中:i1,j1=1,2;i2,j2=1,2,3,4;i3,j3=1,2,3,4,5,6.

图7 x1和x2轴上的吸引子共存Fig.7 Coexistence of attractors on x1 and x2 axes

最后,考虑用H3(x3)取代系统(7)中等式右边的x3,得到如下系统：

(7)

系统(7)将会沿x1、x2和x3轴方向产生共存的混沌吸引子,图8分别给出了n为0、1时的系统(7)的吸引子.

图8展示了2×2×2和4×4×4的吸引子,它们所对应的初始值分别为(2i1-3,2j1-3,2k1-2.8)和(2i2-5,2j2-5,2k2-4.8),其中:i1,j1,k1=1,2;i2,j2,k2=1,2,3,4.

图8 x1、x2和x3轴方向上的吸引子共存Fig.8 Coexistence of attractors on x1 、x2 and x3 axes

通过设置合适的参数系统能够产生其他类型的吸引子.以系统(6)为例,设置参数a=1.1和a=0.98时系统产生的周期共存吸引子如图9所示.

图9展示了通过设置合适的参数而产生的周期共存吸引子.图9a中周期1共存吸引子的初始值为(2i1-5,2j1-5,±0.1),其中：i1=1,2,3,4;j1=1,2,3,4.图9b中周期2共存吸引子的初值为(2i2-5,2j2-5,±0.1),其中：i2=1,2,3,4;j2=1,2,3,4.

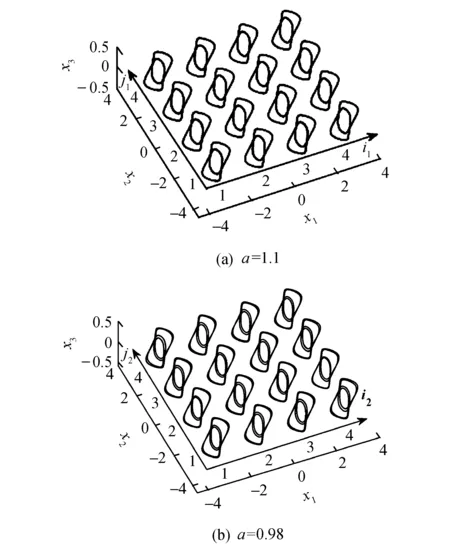
图9 共存的周期吸引子Fig.9 Coexisting periodic attractors

通过上述研究表明,系统(1)在函数(5)的作用下,通过调整n可以改变吸引子共存的生成个数.通常,若沿r个方向来产生吸引子的共存,系统(5～7)生成的吸引子共存个数至少为Nr=(2n+2)r,r=1,2,3.当n→∞时,Nr→∞,即吸引子共存个数趋近于无穷.

总的来说,混沌系统(1)在函数序列(5)的作用下具有复杂的动力学特性.随着初始值的变化,系统在相空间中的轨迹将收敛到不同的混沌吸引子,这种复杂的动态行为所产生的序列在安全通信中有重要的应用潜力.如在图像加密领域,通常选择具有复杂动态行为的混沌系统用来产生伪随机序列，以提高加密的安全性能.基于混沌的加密算法通过选择不同的混沌系统来生成伪随机序列,文献[30]正是利用了此思想.如以系统(7)为例,将整个混沌系统集合作为混沌发生器,则由不同初始值产生的吸引子就等同于混沌集的算法中的不同混沌系统中产生的共存混沌吸引子,这可以提高加密的可靠性和安全性.此外,通过增加n,随着初始条件作为密钥的空间将倾向于无穷大,目前的计算机将很难通过穷举来破译.

4 系统的电路设计

通过选择模拟电路对系统模型(1)进行实验和验证.在此次的电路设计中采用运算放大器、电容、电阻及乘法器(增益为1)进行电路实验.其中,乘法器可应用在实现系统中的非线性乘积项,电容器可应用在实现积分运算中,可借用运算放大器及其相关电阻构成实现加、减以及积分运算模块.基于Multisim实现的电路原理图如图10所示,图中U1=x1,U2=x2,U3=x3.

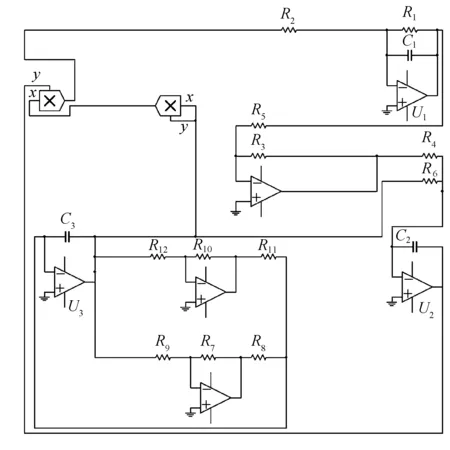
图10 系统模型(1)的模拟电路原理图Fig.10 System model (1) schematic diagram of analog circuit

根据电路定律得到以下微分电路方程：

(8)

将电路方程(8)进行无量纲化处理,令

(9)

式(9)是将方程(8)与系统模型(1)作比较，并作如下取值：

(10)

依据上述数据,对模型系统(1)的电路进行验证,结果如图11所示.

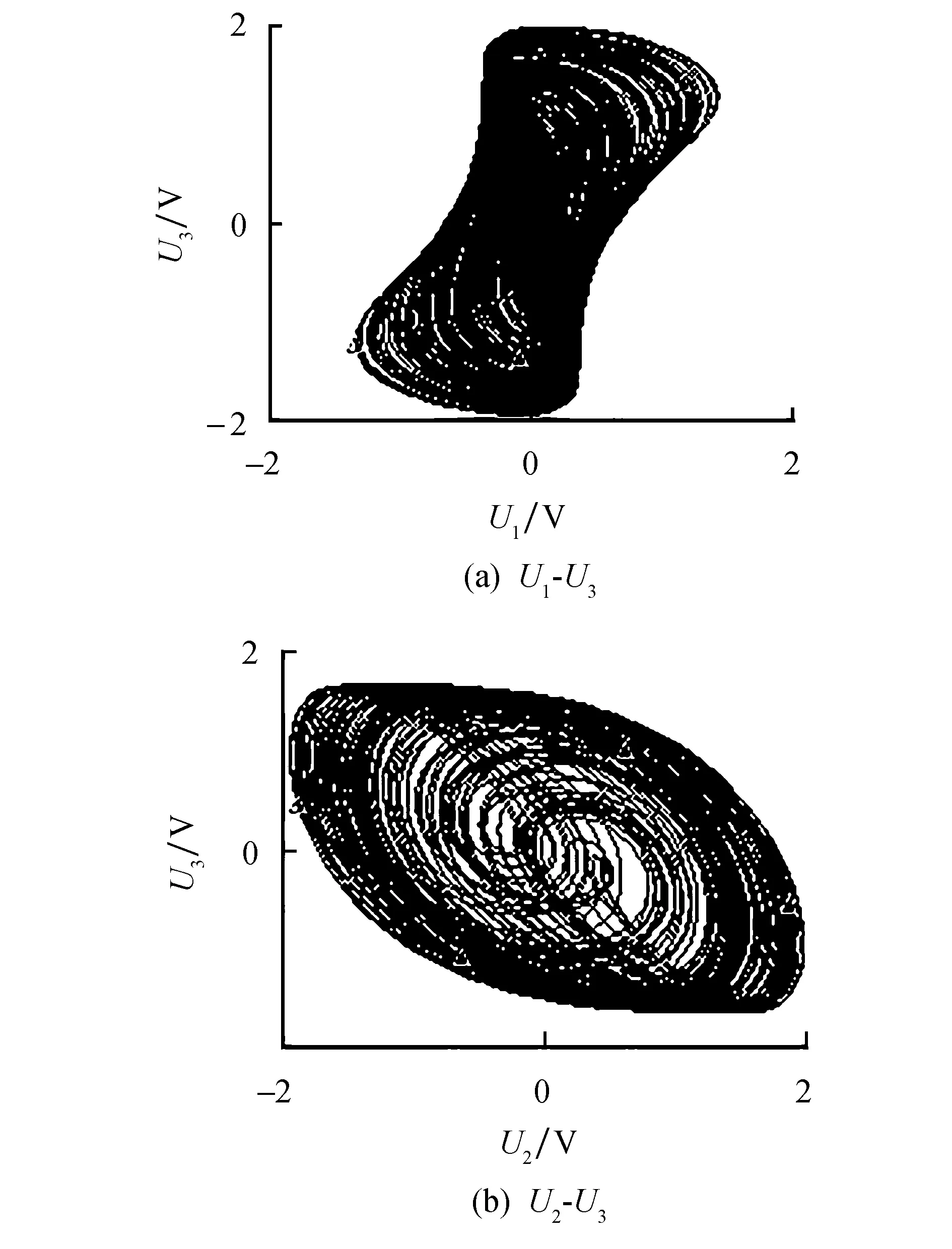
图11 相图Fig.11 The phase trajectory

从图11可以发现,模拟电路仿真结果与系统模型(1)仿真结果一致,表明了所提出的混沌系统模型(1)具有能够实现的可能性.

5 结论

本文在传统混沌系统的基础上构造了一个模型较为简单的混沌系统.通过动力学行为分析了该系统的多稳态性,并在其基础上将双曲正切函数引入该系统,建立了具有可调数目的吸引子的共存.理论研究表明，该系统能够生成无限多个吸引子的共存,并通过数值模拟仿真进行了验证.在上述研究的基础上,得到以下结论：

(1) 从建立具有简单系统和复杂行为的角度出发,建立了一个模型较为简单的混沌系统.

(2) 通过动力学分析验证了该系统具有复杂的多稳态行为.

(3) 将双曲正切函数加入该系统,从而建立了具有可调数目的吸引子共存.

(4) 设计了模拟电路对系统模型进行实验和验证,表明了混沌系统模型具有实现的可能性.

由于该系统的吸引子具有多稳态性和可调数目,较于传统混沌系统具有更为复杂的动力学特性,因此在安全通信等领域有良好的应用潜力.