基于修正Lv模型的低周疲劳寿命预估方法

韦尧兵, 陈书晗, 刘俭辉, 资 绒

(兰州理工大学 机电工程学院, 甘肃 兰州 730050)

疲劳载荷广泛存在于机械设备中,例如航空发动机在运行时,其关键部件高压涡轮盘需要在极端环境中工作.高压涡轮盘众多失效原因中,低周疲劳断裂的失效形式不可忽视[1-3].

国内外相关学者提出了包括M-C方程[4]、Morrow模型[5]、M-H模型[6]及SWT模型[7]等在内的多种寿命预测模型.鉴于平均应力会使材料的疲劳性能变差[8-10]，Morrow[5]利用平均应力修正了M-C方程中的弹性部分,提出了Morrow模型.Manson和Halford[6]将平均应力对材料塑性变形的影响考虑到Morrow模型中,提出了M-H模型,但该模型预估结果精确度低.Smith根据M-H模型,结合新的损伤参量提出SWT模型[11],将最大应力和应变幅作为该参量的主要组成部分,但SWT模型忽略了平均应力效应受材料不同的影响[12]，而Walker[13]考虑了该不足.Lv等[14]建立了Walker指数的计算公式,对SWT模型进行修正并提出Lv模型,但对于某些材料处于较低应力状态时,Lv模型也存在着预估寿命偏保守的问题[15].

本文首先引入材料特性系数m,将Walker指数γ修正为γ′,并将γ′引入到Lv模型中来反映材料特性对疲劳寿命的影响.其次,参考M-H模型对材料塑性部分进行修正,以克服Lv模型未考虑平均应力对材料塑性变形影响的不足.同时，考虑正应变产生的作用,结合应变幅与弹性模量对最大正应力进行修正.此外,由于Walker指数倍数过大会导致材料特性不敏感,使得疲劳寿命预估结果偏保守,所以引入敏感系数k来提高材料受平均应力影响时的反应程度.最后，利用TA11、GH909、FGH96及GH4133合金材料的低周疲劳试验数据,对SWT模型、M-H模型、Lv模型及改进Lv模型的疲劳寿命预估结果进行分析,验证了改进Lv模型的有效性.

1 修正Lv低周疲劳寿命模型

考虑到平均应力对疲劳寿命有较为明显的影响[16-17],Morrow、Manson和Halford基于M-C方程分别提出了Morrow模型和M-H模型，即

式中:εa为应变幅；σ′f为疲劳强度系数；ε′f为疲劳延性系数；σm为平均应力；E为弹性模量；Νf为疲劳寿命；b为疲劳强度指数；c为疲劳延性指数.其中，σ′f、ε′f根据文献[18-19]获得.

但上述模型在估计平均应力影响时存在预估效果较差和适用范围较窄等不足,于是Smith等提出了SWT准则,并将σmaxεa作为损伤控制参数,提出SWT模型，即

(3)

式中:σmax为最大应力值.

Walker引入材料参数γ,解决SWT忽略平均应力可作用于材料塑性变形的问题,其表达式[16]为

(4)

式中:σar为等效对称应力幅；σa为循环应力峰值；R为应力比.

基于Walker指数和SWT模型,Lv提出新的疲劳寿命预估模型,其表达式为

(5)

Lv利用不同材料的性能参数进行分析,发现γ值与材料的σ0.2和σb有一定的关联,且当σ0.2与σb数值接近时,γ值约为0.5.于是提出Walker指数的计算方式为

(6)

式中:σ0.2为屈服强度；σb为抗拉强度；+和-可参考同类材料实验值进行选择.

但不同材料的γ值需要大量实验来获得,因此Lv模型应用范围有限[19].

1.1 材料特性系数m的确定

由于Walker指数γ值与材料σ0.2和σb有关,所以考虑材料力学特性对γ的影响,引入材料特性系数m对式(6)进行修正.m表达式和修正后表达式分别为

式中:m为屈强比,反映材料塑性变形能力,其值越大,则塑性越差；γ′为修正后Walker指数.

考虑到正应变对疲劳寿命产生的影响,利用应变范围Δε和弹性模量E对最大应力进行修正,即

式中:σ′max为修正后最大应力.

1.2敏感系数k的确定和塑性变形的修正

基于Lv模型,引入新Walker指数γ′和最大应力σ′max对式(5)进行修正,即

(11)

利用式(11)对7075-T651、1Cr11Ni2W2Mo-V及碳钢3种材料[19]进行疲劳寿命预估,结果如图1所示.

从图1可以看出,式(11)的预估结果较差,主要原因是Walker指数倍数过大,使得寿命预估偏于保守.于是引入与材料σ0.2和σb相关的敏感系数k,

图1 疲劳寿命预估结果分散带Fig.1 Scatter band of fatigue life prediction results

利用2k倍的Walker指数γ进行平均应力修正,反映材料受平均应力影响时的反应程度,并提高材料的敏感度.修正后表达式为

(12)

k值与σ0.2和σb有关,即

(13)

其中，

(14)

由此可见,k值越小,材料对平均应力影响的反应越敏感.误差因子n与修正前、后的损伤控制参量比值和材料特性相关,反映了因材料力学特性不同所导致实际与预测寿命之间的普遍误差.

通过对7075-T651、1Cr11Ni2W2MoV、TC4及碳钢4种材料[15,19]的验证,n值分布如图2所示.

从图2可以看出,n值的取值范围为0.5～1.0,同时n值可参考同类材料进行选取.

图2 最大应力与误差因子n关系图Fig.2 Relationship between maximum stress and error factor n

考虑到平均应力对材料塑性变形的影响,参照M-H模型,利用平均应力对式(12)塑性变形部分进行修正[15],最终疲劳寿命预估模型表达式为

(15)

2 新疲劳寿命模型的验证

2.1 修正后γ′计算方法的验证

利用FGH96、GH909、TA11及GH4133合金对修正后γ′计算方法进行验证.由文献[19]可得Walker指数的实验计算值γ1.将修正后的Walker指数γ′和Lv模型计算所得的γ2分别与γ1进行对比,误差结果如表1所列.除FGH96[15]外,其他3种材料相关参数可由文献[19]获得.

从表1可以看出,新Walker指数γ′的相对误差平均值为6.52%,精度更高.

表1 γ1、γ′及γ2值对比Tab.1 Comparison of γ1、γ′ and γ2 values

2.2 材料性能参数

利用不同应力比下的FGH96、GH909、TA11及GH4133合金的低周疲劳试验数据[15,19],分析对比改进Lv模型、M-H模型、SWT模型及Lv模型的寿命预估结果.FGH96、GH909、TA11及GH4133合金相关材料参数如表2所列,其中材料参数b和c可利用相关文献[17]获得.

表2 材料性能参数Tab.2 Material performance parameters

2.3 新模型的疲劳寿命分析

由改进Lv模型、M-H模型、SWT模型、Lv模型计算得到的上述材料预测寿命分别为Nf1、Nf2、Nf3、Nf4,结果如表3所列[14-15].

表3 实验疲劳寿命与预测疲劳寿命Tab.3 Fatigue life test value and predicted value

不同应力比下,4种不同材料疲劳寿命对比结果如图3和图4所示.

对处于对称应力载荷下的不同材料进行寿命预估.从图3可以看出,改进Lv模型、M-H模型及SWT模型的疲劳寿命预估结果与实验结果一致性较高,基本处于2倍分散带内,均适用于TA11和GH909合金的疲劳寿命预估,但Lv模型对TA11和GH909合金均不适用.

图3 对称应力下的疲劳寿命分散带Fig.3 Fatigue life dispersion band under symmetrical stress

对处于非对称应力载荷下的不同材料进行寿命预估.从图4可以看出：改进Lv模型的疲劳寿命预估结果基本在2倍分散带内,均适用于FGH96和GH4133合金的疲劳寿命预估;M-H模型对FGH96和GH4133合金均不适用;SWT模型较适用于FGH96合金的疲劳寿命预估，但对GH4133合金的疲劳寿命预估效果较差;Lv模型对GH4133合金的疲劳寿命预估结果在2倍分散带内,但对FGH96合金的疲劳寿命预估效果较差.

综上所述,改进Lv模型适用于不同应力比条件下、不同材料的疲劳寿命预估,M-H模型、SWT模型及Lv模型只适用于部分应力比条件下、部分材料的疲劳寿命预估.改进Lv模型在预估精度和适用性等方面均具有较大优势.

定义EN为预估误差因子[20],其表达式为

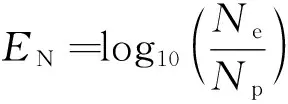
(16)

式中:Ne为实验寿命；Np为预测寿命.

定义f(x)为误差概率密度函数,其表达式为

(17)

式中:δ为EN的标准差；μ为EN的平均值.

利用遵循正态分布的误差概率密度函数f(x)对疲劳寿命预估结果进行误差分析,如图5所示.

图5 疲劳寿命误差分析Fig.5 Fatigue life error analysis

可以看出:改进Lv模型的误差概率密度均集中在0值附近,分散性较好；M-H模型可以较好地对TA11和GH909合金进行疲劳寿命预估，针对GH909合金的疲劳寿命预估,误差概率密度明显集中在0附近,但对FGH96和GH4133合金的疲劳寿命预估效果很差,分散性很差；SWT模型对TA11和GH909合金的疲劳寿命预估效果较好,误差概率密度集中在0附近,且分散性好,对GH4133合金的疲劳寿命预估效果一般,且对FGH96合金的疲劳寿命预估效果差；Lv模型则对GH4133合金的疲劳寿命预估效果较好,但对TA11、FGH96及GH909合金的疲劳寿命预估效果较差,误差概率密度集中在0.6附近.综上所述,改进Lv模型因其误差小、分散性好而具有较高精确度和较广适用性.

3 结论

1) 利用材料特性系数m来修正Walker指数,并考虑单轴拉压中正应变的影响来修正最大正应力;同时,引入敏感系数k来提高材料受平均应力影响时的反应程度;此外,参考M-H模型对塑性部分的修正,修正了Lv模型中的塑性变形部分.根据以上修正提出基于改进Lv模型的寿命预估模型.

2) 为验证γ′的准确性,使用多种材料的γ与γ′进行对比,得到改进计算值的平均误差为6.52%,比原Lv模型误差小1.45%,证明改进计算方法有较高的准确性.

3) 利用TA11、GH909、FGH96及GH4133合金材料的疲劳试验数据来验证改进Lv模型.结果显示,与SWT模型、M-H模型及Lv模型3种模型相比,改进Lv模型能较好地适用于不同应力比条件下、不同材料的疲劳寿命预估,疲劳寿命预估结果均分布在2倍分散带内,且大部分与实验寿命相近,并且误差概率密度集中分布在0附近.因此，验证了改进Lv模型的有效性,表明该模型在预估精度和适用性方面均具有较大优势.但同时,本文所用的实验数据相对较少,对模型的验证有所限制,今后将在新的研究中对其展开讨论.