巧用“数形结合”妙解数学难题

李亚 西藏林芝市第一小学

“数形结合”思想在整个数学历史长河中十分经典，从小学生的思维特点来看，学生的逻辑思维与抽象思维还在初步阶段，数形结合的引入不仅符合了学生的学习需求，而且也助力知识难度的降低。数学是一门抽象性与逻辑性较强的学科，尤其对中高年级的小学生来说，数学概念、定义与习题的交叉融合亟需借力数形结合直观手段。因此，数学教师应当有意识地引导学生形成良好的“数形结合”思想，让学生逐步形成灵活的思想能力，从而高效化解数学难题。

一、“数形结合”思想在小学数学教学中的渗透意义

在传统的数学教学中，多数教师由于受到应试教育的影响常常采用“照本宣科”的“语言灌输法”，强制性要求学生记忆知识、定理，长期的被动学习导致学生在数学学习中形成了套用思维，面对新的题型或者问法便会不知所措。究其根本，是因为数学本质的不清晰。“数形结合”巧妙地打破了传统教学模式的弊端，教师需要改变以往的“语言授讲”法，而是要将复杂的数量关系以形象的图形展现给学生，由此一来，学生将会清晰掌握知识脉络，在牢牢把握知识本质的基础上学会辨别复杂的数学问题。与此同时，学生遇到条件较多的题目时也可以借助数形结合的方式梳理条件，以此增强自身的学习能力和发散性思维。

二、“数形结合”思想在小学数学教学中的渗透路径

（一）数形结合，明晰概念

“数形结合”思想是解决数学问题的重要手段，其将形与数充分融合，能够直观呈现出数学概念。概念类习题在数学领域中数不胜数，随着学生年级的增长，学生接触的数学概念也越来越多，于是使多数学生在面对数学问题时很难准确把握其中蕴藏的概念定义，导致了解题未果。介于此，数学教师可以利用“数”与“形”的密切关系将抽象的概念直观化，以图形辅助的方式降低习题难度，从而促使学生在愉悦的状态下轻松解题。

图1

（二）数形结合，理解算理

“计算”是数学课程领域中的重要分支，那么算理的掌握直接决定了学生的整体学习质量。四年级数学计算已经上升了一个梯度，学生仅仅依靠记忆的算理很难找到解题技巧。因此，教师需要引导学生借助图形分析题目，化解计算题的算理逻辑，由此梳理出清晰的解题思路，灵活掌握固化的计算方式。

以四年级数学上册第4单元《三位数乘两位数》为例：“李叔叔从某城市乘坐火车去往北京用了12个小时，已知火车平均每小时行驶145千米，那么请问某城市到北京有多少千米？”此时，教师可以借助线段图（见图2）帮助学生分解题目中的条件，指导学生快速准确地列出算式。直观形象的习题计算也会瞬间点燃学生的探究兴趣，所以教师趁此契机把握学生的注意力与学习兴趣引出“估算过渡”。首先，教师引领学生估算“145×12”的大致结果，使学生将145看做150，将12看做10，于是根据150×10估算出1500；或者教师引导学生只将12看做10，进而估算出145×10=1450。接着，在学生估算完成后，教师再引出“三位数乘两位数的笔算方法”（见图3），从而有效增进了学生的算理掌握，使学生巧妙化解了难题。将题目中的已知数据以线段的形式展现出来，一来具化了抽象的数字，二来整理了已知和未知的数据，能够更加容易地找到解答方法，这种数形结合的方式在提高准确率的同时，还减轻了学生的学习压力。

图2

图3

（三）数形结合，拓展思维

数学问题中往往存在了一些隐形条件，这些隐藏的数学规律往往是学生解题的关键。小学中高年级学生的理解能力和辨别能力还有所欠缺，所以学生需要借助数形结合思想找出题目中的隐藏条件，以此在发散思维的基础上寻找恰当的解题思路，从而巧妙化解难题。

以四年级数学上册第5单元《平行四边形和梯形》为例，在学习本节内容之前，学生已经学习了有关四边形的知识，本节需要学生重点掌握平行四边形的特点以及平行四边形与正方形、长方形的关系。教师可以运用集合图（见图4）的方式帮助学生理解学过的四边形之间的关系，使学生在直观的集合图中发散思维，清楚地将四边形分类，由此有效掌握了平行四边形和梯形的定义。之后，教师出示问题：“在梯形里画两条线段，将它分割成三个三角形，那么你会如何分割？”题目中提到的“画两条线段”出现了多种可能性画法，所以学生可以借助图形分析出其中的隐藏画法，从而培养了学生对“数形结合”的应用意识，并促使学生发展空间观念。此处“数形结合”思想的应用，借助了图形特有的转化关系，这是单纯的数字无法体现的，应用数形结合方式后，学生便能一眼看出各元素所包含范围的大小及彼此之间的关系，对概念的理解会更加深刻，在学习时也会更具逻辑性，增强学生的逻辑思维。

（四）数形结合，化繁为简

借助华罗庚先生的话说：“数形本是相倚依的，焉能分作两边飞。”数形结合思想是指抓住数与形本质上的联系，将抽象的数量关系与直观的图形整合考虑，降低思维难度，所以小学数学教师可以引导学生借助数形结合思想将繁杂的问题简单化，由此帮助学生攻克难点，树立学习数学的信心。

以五年级上册第2单元《位置》为例，教师要认识到“位置”中坐标系的重要价值，引导学生学会将复杂错乱的数据放到坐标系中再去解答。教师出示题目“优优和乐乐一起玩‘寻宝’游戏，两人从同一个地点分别出发，优优向东偏北30°方向走200米找到第一个宝藏，乐乐向西偏南30°方向走300米找到第二个宝藏，现在，优优要去到乐乐的位置，与乐乐一起找到第三个宝藏，问优优要怎么走？”对此，教师可以引导学生画出位置关系图（见图5）。

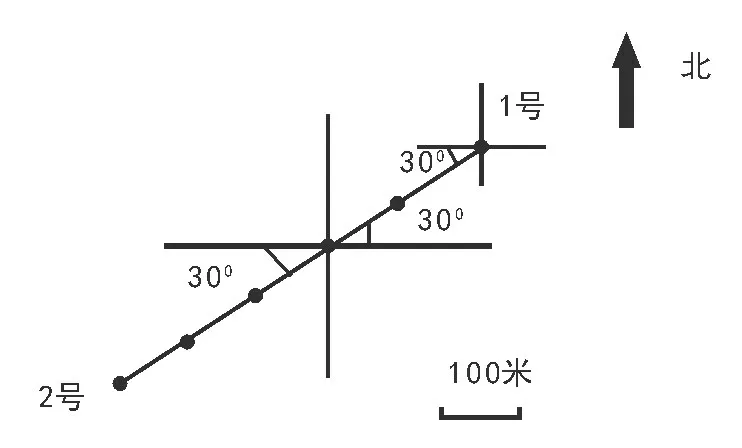
图5

绘制出坐标图形，位置间抽象关系的难度就会降低，学生便可以直观地看到优优和乐乐的位置与走向，得出“优优要向西偏南30°的方向走500米才可以与乐乐汇合。”通过坐标图的呈现，学生在既不混乱也不出错的情况下，直观推理出第三个宝藏的正确位置，由此有效增强了逻辑推理能力。

结语

“数形结合”思想在小学数学中的渗透使概念、习题等数学内容不再沉闷单调，而以“形”与“数”的相互转换使知识更加具有趣味形和直观性，由此进一步提升了学生的解题能力。学生在学习知识的同时，思维得到拓展，因此，数学教师在教学中更加应该重视数学思想的渗透，引导学生逐步养成终身发展的思想意识，从而为今后的综合性学习奠定扎实的基础。