堰塞坝溃决过程中孔隙水压力变化规律

李霄， 陈华勇,3*， 阮合春， 俞昀晗

(1.中国科学院山地灾害与地表过程重点实验室/中国科学院水利部成都山地灾害与环境研究所， 成都 610041； 2.中国科学院大学， 北京 100000； 3.中国科学院青藏高原地球科学卓越创新中心， 北京 100101)

堰塞坝是一种未经专门设计、无特定泄洪道的天然土石坝，其几何形态、物质组成、内部结构均与人工土石坝存在显著差别[1]，溃决可能性远高于人工土石坝，仅有极少数能长时间保留[2]。堰塞坝一旦溃决，产生的非常规模洪水将对下游的生命财产安全造成严重危害。

目前，蒋先刚等[3]通过研究不同沟床坡度堰塞坝溃决过程，指出沟床坡度为12°时堰塞坝溃口更易失稳，坝体溃决过程相对更快；赵高文等[4]基于堰塞坝溃决试验，对比分析了不同密实度条件下的堰塞坝溃决过程差异；王道正等[5]根据不同颗粒级配下的堰塞坝溃决过程，认为内部土体颗粒平均粒径较大的堰塞坝相对容易溃决。这类堰塞坝试验研究虽然考虑了单一因素对堰塞坝溃决过程的影响，但很少对堰塞坝溃决过程的展开直观量化的分析[3-13]。而如Chang等[14]提出了一种基于物理过程的堰塞坝漫顶溃决模型，模拟了土壤可蚀性随深度变化对侵蚀过程的影响；Shen等[15]除了考虑土壤可蚀性随深度的变化，还考虑了侵蚀模式(单侧溃坝和双侧溃坝)及坝体不同物质组成；Cao等[16]基于浅水动力方程，建立了堰塞坝溃决二维模型，这些模型虽然更为直观的分析了堰塞坝的溃决过程，却没有考虑坝体内部孔隙水压变化对溃决过程的影响。

而目前关于孔隙水压力的研究则主要集中于对尾矿坝、土石坝稳定性的分析。Zhang等[17]研究了不同固结条件下尾矿坝动孔隙水压力的演化规律；韩雪等[18]模拟计算了不同降雨强度、不同水位条件下尾矿坝中的孔隙水压力的变化；Mouyeaux等[19]、Day等[20]、陈继平等[21]、陈立宏等[22]研究了土石坝心墙中孔隙水压力的变化过程；尚敏等[23]基于滑坡失稳破坏特征，结合有效应力原理提出了孔隙水压力变化速率条件下滑坡失稳破坏的模式，得出孔隙水压力对滑坡破坏的影响。与尾矿坝、土石坝相比，堰塞坝内部物质组成相对较为复杂，因此基于尾矿坝、土石坝等工况建立的模拟模型是否适用于堰塞坝仍需要进一步的探究。

事实上，堰塞坝的溃决是一个坝体外部溢流冲刷与坝体内部流(水)固(土)耦合渗流共同作用的结果，堰塞坝上游水位的急剧变化造成坝体渗流情况的改变，进一步改变着坝体内部的孔隙水压力，最终体现为因土体有效应力的变化而影响溃决发展过程，详细阐明溃坝机理才是提高数模结果可靠性的关键[24-28]。因此，现通过水槽模型试验，重点分析堰塞坝溃决过程中孔隙水压力的变化过程，通过数值模型直观的验证二维饱和渗流非稳定方程拟合蓄水期堰塞坝孔压变化的可靠性，并探讨三维孔压模拟分析的可行方向，进一步加深对堰塞坝溃决机理的认识。

1 研究方法

1.1 模型布置

试验在中国科学院水利部成都山地灾害与环境研究所的实验大厅内进行。试验装置主要由供水系统、主水槽、废料池组成，均为钢结构，如图1所示。试验水槽用于模拟主河道，长4.0 m、宽0.4 m、高0.4 m、纵坡为1°，两侧为透明钢化玻璃，可直接观测到水槽中的试验现象。水槽首端接一个可调节来水流量的供水箱(1.0 m×1.0 m×1.0 m)；末端接一废料池(1.2 m×1.2 m×0.4 m)，可进行废料的回收利用。堰塞坝布置于水槽中部，坝高0.4 m，坝顶宽度0.2 m，上下游坝坡分别为45°和20°。为了便于观测溃口的发展过程，在坝顶最左侧人为开挖一条垂直于坝轴线、横断面为矩形(4 cm×4 cm)、纵坡为0°的泄流槽，引导水流从此处发生单向侧蚀，如图3所示。

图1 试验装置布置图Fig.1 Layout of test device

1.2 方案设计

1.2.1 试验材料参数

为使试验成果能够更好地反映实际情况，选取汶川地震灾区泥石流原样土作为试验坝体材料。因试验为小尺度，水动力条件有限，所以难以考虑全级配(较大颗粒)，故本实验筛除2.0 cm以上的粒径，颗粒级配如图2所示。坝体初始含水量设置为12.0%，容重为1.98 g/cm3，来水流量为1.5 L/s，最大库容为0.32 m3。

1.2.2 仪器布设

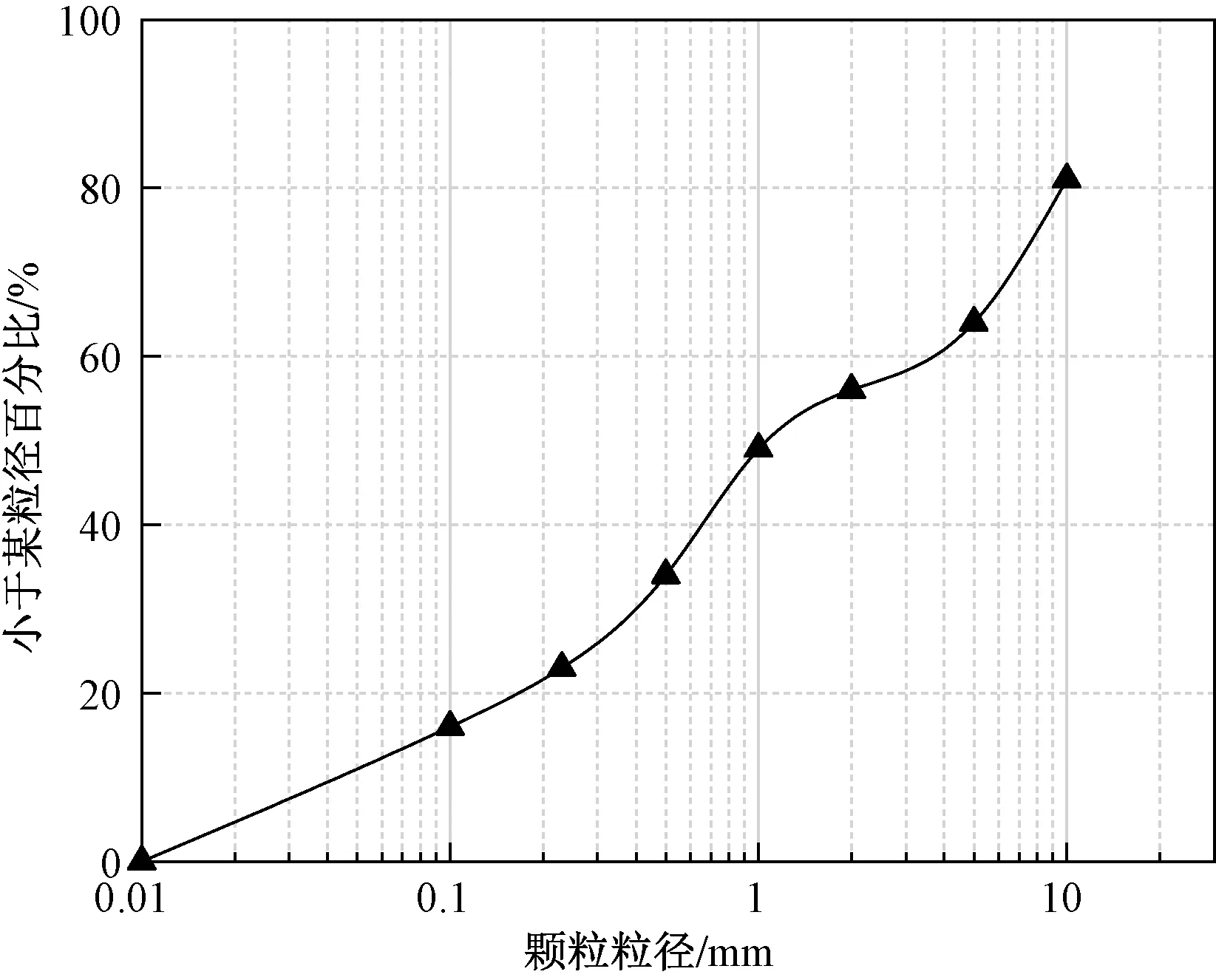
图2 试验土体颗粒级配曲线Fig.2 Grain gradation curve of test soil

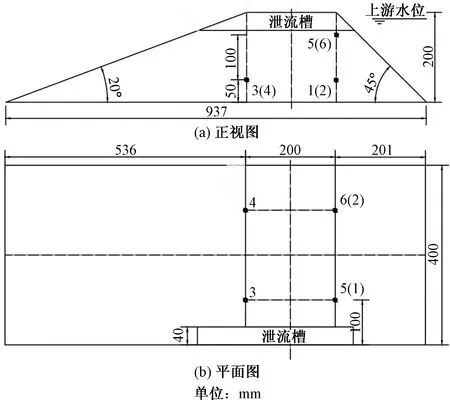
图3 堰塞坝体型及传感器测点布置图Fig.3 Barrier dam shape and sensor measuring point layout

本实验在堰塞坝体内部共埋设6个型号为485-20的孔隙水压力传感器，编号为1～6，其中，1、2、3、4号测点位于距离坝底5.0 cm的水平面内，5、6号测点位于距离坝底15.0 cm的水平面内，各传感器位置如图3所示，图3中括号内的测点为投影面重影点中的不可见点；数据采用计算机自动采集，采集频率为10.0 Hz。测试过程中，分别在坝体顶部、下上游、左侧各架设一台4 K高清摄像机对溃决过程进行实时记录。溃决流量则通过在坝前水槽底部布设一个孔隙水压力传感器，测出水位的变化过程，最后根据水量平衡方程计算出溃决流量变化过程。

2 试验成果分析

2.1 堰塞坝溃决过程

坝体溃决时的洪峰流量大小直接决定了溃决洪水的灾害程度，而溃决洪水过程又与堰塞坝溃决过程(或溃口发展过程)密切相关。准确描述堰塞坝溃决过程是精确计算溃决洪水的关键前提条件。通过试验研究，根据溃口发展特征，可将堰塞坝的溃决过程分为三个阶段：坡面侵蚀阶段(阶段Ⅰ)、溯源陡坎侵蚀阶段(阶段Ⅱ)、粗化再平衡阶段(阶段Ⅲ)，其中，阶段Ⅱ发展最为剧烈；溃决洪水呈现先增后减的时程变化(图4)。

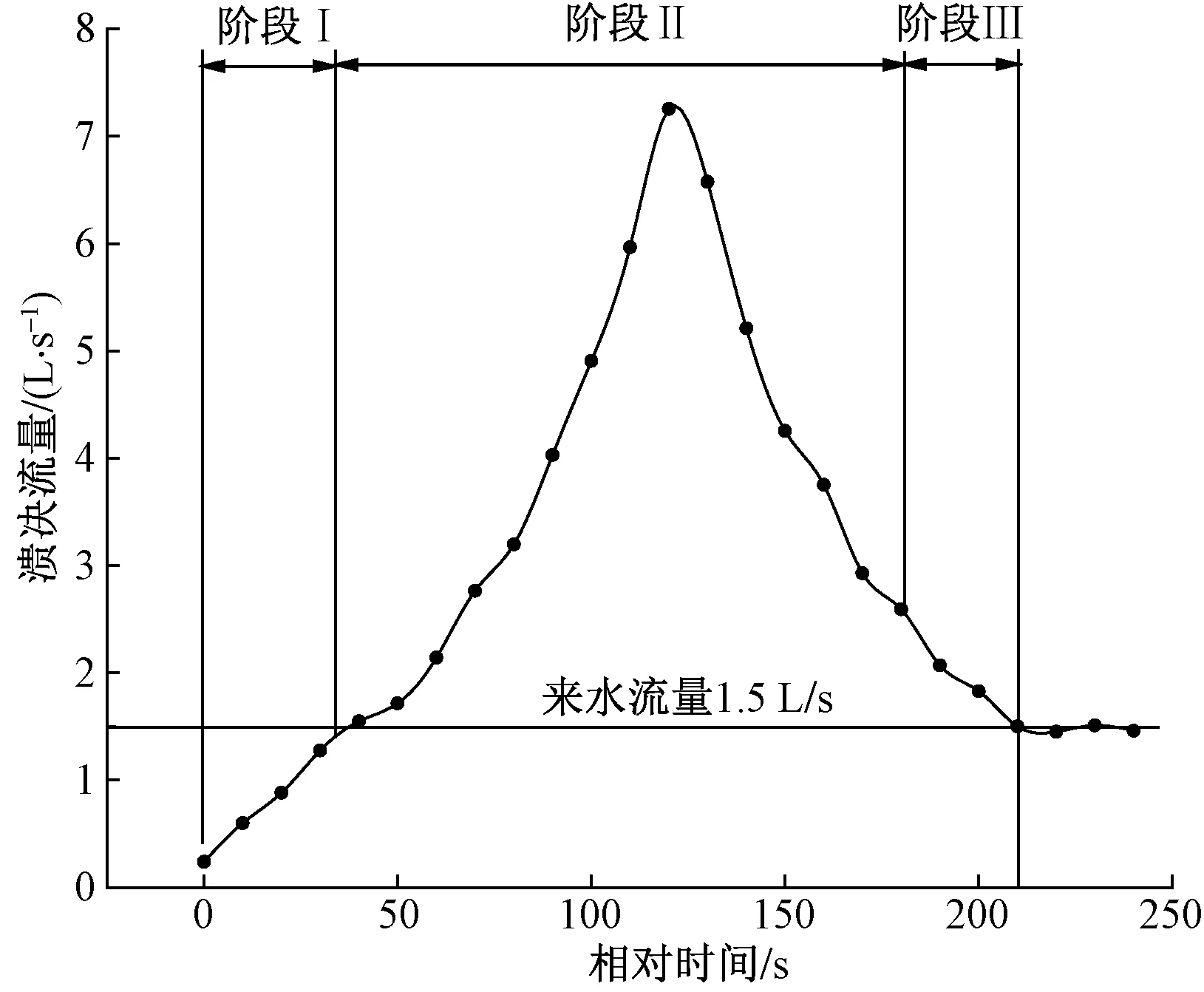
图4 堰塞坝溃决流量变化过程Fig.4 Variation process of barrier dam break discharges

2.1.1 阶段Ⅰ(坡面侵蚀)

坡面侵蚀阶段为坝体开始溢流至溯源陡坎刚开始形成这一过程(0～32 s)，此阶段中溢流量不断增加，但始终小于入库流量，最大流量仅为1.38 L/s，水位不断上涨。坝顶开始溢流后，因坝顶为平坡，水流流速较小，水流侵蚀速率并不明显，水体清澈透明。当水流到达下游折坡点A后，势能向动能转化加大流速，侵蚀能力明显增强，中细小颗粒被带走并大量堆积于坡脚，形成一个新的堆积扇[图5(a)]，坡面大颗粒(粒径约2 cm)不断出露，形成了具有显著消能作用的多级阶梯-深潭系统[图5(b)]，抑制了坡面的侵蚀。

图5 阶段Ⅰ特征现象Fig.5 Characteristic phenomena of stage I

当溃决流量进一步加大后，流速随之增大，坡面上游大颗粒(粒径约2 cm)被启动，运动过程中受坡面下游大颗粒的阻碍后堆积于此，合并为一个更大的阶梯-深潭系统[图5(c)]，此时阶段Ⅰ结束，该深潭的位置即为溯源陡坎侵蚀的起始点，进一步发展后将形成溯源侵蚀陡坎，同时该位置也是坡脚堆积体与坝坡的折坡点。

2.1.2 阶段Ⅱ(溯源陡坎侵蚀)

溯源陡坎侵蚀为溯源陡坎刚开始形成至溃口完全贯通这一过程(32～160 s)。此阶段中，溃决流量先增后减，几乎大于来水流量，在T=145 s时出现峰值流量达7.25 L/s，为来水流量的4.8倍。如图6(a)所示，溯源陡坎侵蚀的起始点形成后，深潭底部和上缘被入潭水流不断侵蚀下切，历时15 s后侵蚀至坝底，形成明显陡坎，角度为53°；深潭内高含沙水流紊动剧烈，形成一个明显的顺时针横轴旋滚，配合入潭的高速水流，整个陡坎向上游快速移动，并伴随着溃口岸坡的间歇性坍塌；在潭内剧烈紊动的消能作用下，出潭水流流速大幅降低，大量泥沙颗粒在深潭下游停淤，细小颗粒主要以悬移质的形式被水流携带至下游河床，此过程历时约100 s。

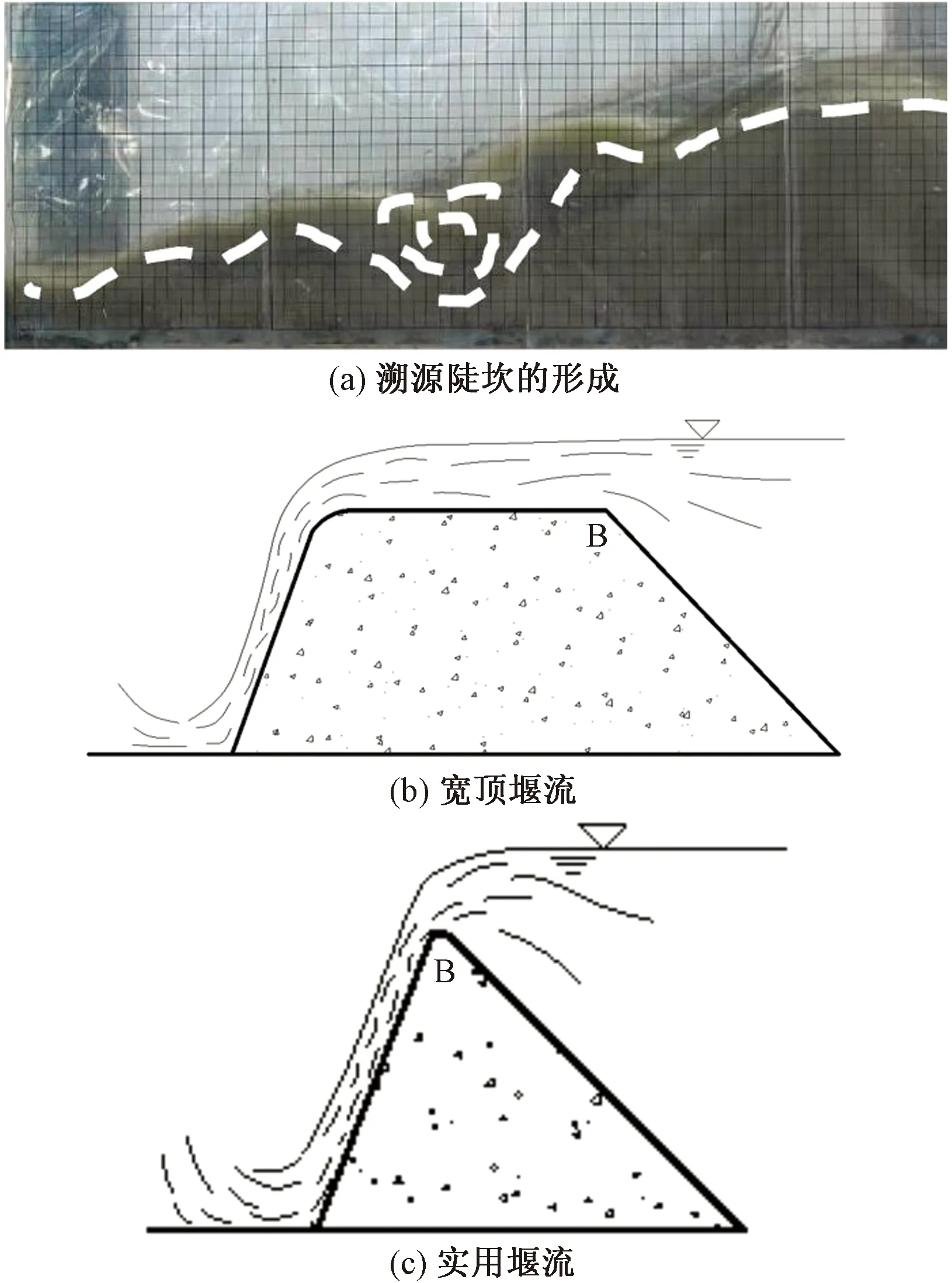
图6 阶段Ⅱ特征现象Fig.6 Characteristic phenomena of stageⅡ

当陡坎后移至上游坝坡B点时，过坝漫溢水流实现了从宽顶堰流到实用堰流的转化[图6(b)和图6(c)]，坝顶顶托作用减小，过坝漫溢流速加大，溃口迅速下切至侵蚀基准面(图8)，溃口完全贯通，溃决流量达到最大，随后不断减小。此过程中，溃口单向侧蚀速率大幅提高，岸坡坍塌频率加大(图7)。当溃口下切至侵蚀基准面时，阶段Ⅱ结束。

2.1.3 阶段Ⅲ(粗化再平衡)

粗化再平衡阶段为从溃口下切至侵蚀基准面(图8)时到溃决流量达到稳定时这一过程(160～215 s)。此阶段中，上游水位逐渐降低并趋于平稳，溃口底部颗粒不断粗化，水体清澈透明，溃决流量等于来水流量。残余坝体稳定，溃口底坡趋于平整，达到新的冲淤平衡。但由于残余坝体具有明显的束窄河床作用，流速矢量的改变极易造成岸坡的淘刷。

图7 溃口岸坡间歇性坍塌Fig.7 Intermittent collapse of breach slope

图8 侵蚀基准面Fig.8 Erosion datum

2.2 孔隙水压力的变化过程

2.2.1 孔压的总体变化趋势

为了直观反映堰塞坝的溃决过程对坝体内部孔隙水压力的影响，测试时，待坝体堆筑完成后，采集此时各孔隙水压力传感器的数值作为零点值，并界定开始蓄水时为初始时刻，此时实验历时T=0 s，各传感器测点的孔压值均为0 kPa，当实测孔压为负值时，表明实测孔压小于初始孔压，反之则反。需说明，这里的0时刻(开始蓄水)与1.1节中的0时刻(开始溢流)定义不同。试验研究发现，堰塞坝溃决过程中各测点孔隙水压力的变化过程均呈现先增后减的变化趋势，如图9所示。

以测点1为例，开始蓄水(T=0 s)后，上游水位不断雍高，但蓄水初期(0～60 s)浸润线尚未达到测点1位置，孔隙水压力保持不变。

T=60～140 s时，浸润线抬升至测点1以上，但因上下游水头差较小，加之渗径较长，孔隙水压力增长缓慢；随着上游水位的不断升高，上下游水头差不断增大，渗径减小，渗流速度不断加大，致使孔隙水压力快速增长。

T=272 s时，上游达到最高水位(21 cm)，此后上游水位随溃口的发展不断下降，但孔隙水压力在T=272～283 s时仍持续上升，说明孔隙水压力的变化存在明显的滞后现象。

T=283～330 s，溃口侵蚀速率加快，上游水位急剧下降，孔隙水压力大幅下降，同时由于坝体内横向浸润线呈“驼峰”状，存在严重的反向渗流，进一步削弱了坝体稳定性，加快了溃决过程，在上游坝面可观察到明显的滑动现象，这也是土石坝在运行调度过程中不允许水位骤降的主要原因。

T=330 s时，溃口下切至1号传感器位置，将传感器带出，孔隙水压力出现突变，溃决过程接近尾声。

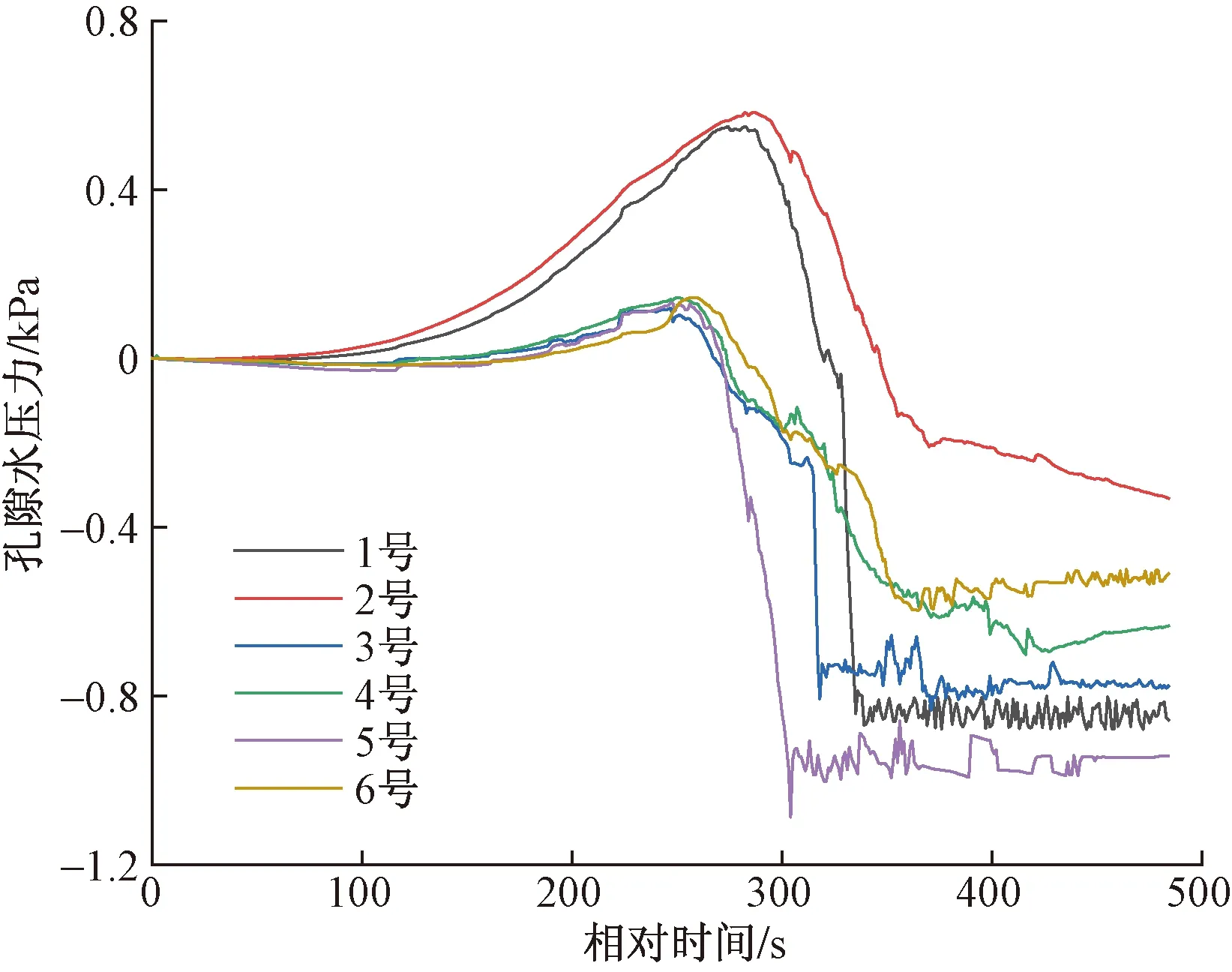
图9 堰塞坝孔隙水压力变化过程Fig.9 Variation process of pore water pressure in barrier dam

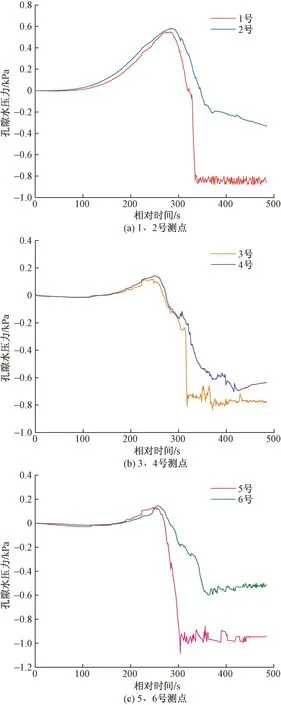
图10 坝体纵向孔隙水压力变化图Fig.10 Variation of longitudinal pore water pressure in barrier dam

2.2.2 坝体纵向孔压的变化

以图10中同一纵断面相同高程1号(右岸)、2号(左岸)测点为例，在蓄水阶段、坡面侵蚀阶段及溯源侵蚀陡坎的形成阶段，即孔压达峰值前，因溃口发展较为缓慢，左右岸水头差并不明显，渗流路径主要平行于横断面，两测点孔压值较为接近；随着阶段Ⅱ中溯源侵蚀陡坎后移及溃口的快速下切贯通，溃口右侧岸坡演化为坝体的一个新鲜渗流自由逸出面，渗流在上下游及左右岸水头差的共同作用下发生从二维到三维流动的转化，因此，在该过程中，2号测点的孔隙水压力始终大于1号测点，可以说溃口演化过程对坝体孔隙水压力(或渗流)起着决定性作用，这也是目前还难以构建数学模型分析溃决过程中坝体渗流的主要原因。此外，因3号、4号测点处于其余测点的下游位置，对孔压敏感程度较低，故变化趋势不显著。

2.2.3 坝体横向孔压的变化

以图11(a)中同一横断面内相同高程的1号(上游)、3号(下游)测点为例，在堰塞坝溃决过程中，1号测点的孔隙水压力值远大于3号测点，峰值(0.55 kPa)为3号测点(0.12 kPa)的4.6倍，表明下游测点对孔隙水压力的敏感程度较上游测点明显降低。此外，由于坝体左侧存在溯源陡坎侵蚀，下游侧3号传感器首先被溃口水流带出，故3号测点孔隙水压力值的突变先于1号测点。此外，因2、4号测点处于残余坝体内部，未被溃口水流带出，故孔隙水压力未出现突变，其余规律与1、3号测点类似[图11(b)]。

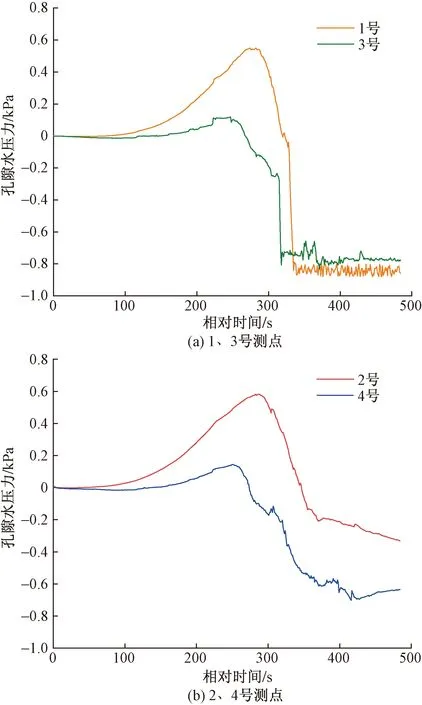
图11 坝体纵向孔隙水压力变化图Fig.11 Variation of longitudinal pore water pressure in barrier dam

2.2.4 孔压的理论分析

在开始蓄水至堰塞坝未开始溢流阶段，渗流仅在上下游水头差的作用下平行于坝体横断面方向运动，下游坡面为渗流的自由逸出面。可由饱和非稳定二维渗流的基本微分方程进行求解[29-31]。

其中，Kx≈Ky≈Kz≈9.1×10-4cm/s由实验测得，分别表示沿x、y、z方向的渗透系数；单位储存量Ss(1 L/s)为单位体积饱和土体在水头下降1 m时，因土体压缩和水体膨胀释放的水量，而对于开始蓄水至堰塞坝未开始溢流阶段，水位上升时，由土体压缩和水体膨胀排除的水量与土体吸水饱和的所吸收的水量相比较小，故可令Ss=0。即

(1)

(2)

式中：h为研究时段坝前水头，m；t为研究时段时长，s。

通过建立数值模型，对2、4、6号三个测点所在孔隙水压变化较大的截面的孔隙水压进行计算，量出浸润线至测点垂直距离，得到水位上升过程中各测点的孔隙水压力变化情况(表1)，并与实测值进行对比(图12)，表明饱和非稳定二维渗流微分方程可用于模拟分析蓄水期中的坝体孔压变化趋势。

考虑到，在溃决过程中，当坝顶出现溢流后，溃口边坡演化为渗流的自由逸出面，渗流发生了从二维到三维的转化，此时可采用饱和非稳定三维渗流的基本微分方程进行求解：

(3)

但与一般三维渗流不同的是，溃口边坡并不是固定的，而是随水流的侧蚀和下切呈现非线性移动，并伴随间歇性不同规模的滑塌；只有合理定量描述堰塞坝溃口侧向展宽过程，才能准确定义堰塞坝溃决过程中的渗流逸出面边界条件，进而求解出孔压的变化过程。该问题将在后续进一步研究。

3 结论

通过水槽模型试验，分析了堰塞坝在漫顶溢流溃决模式下坝体内部孔隙水压力的变化过程，最终得出以下结论。

表1 蓄水期孔压计算结果Table 1 Calculation results of pore water pressure in impoundment period

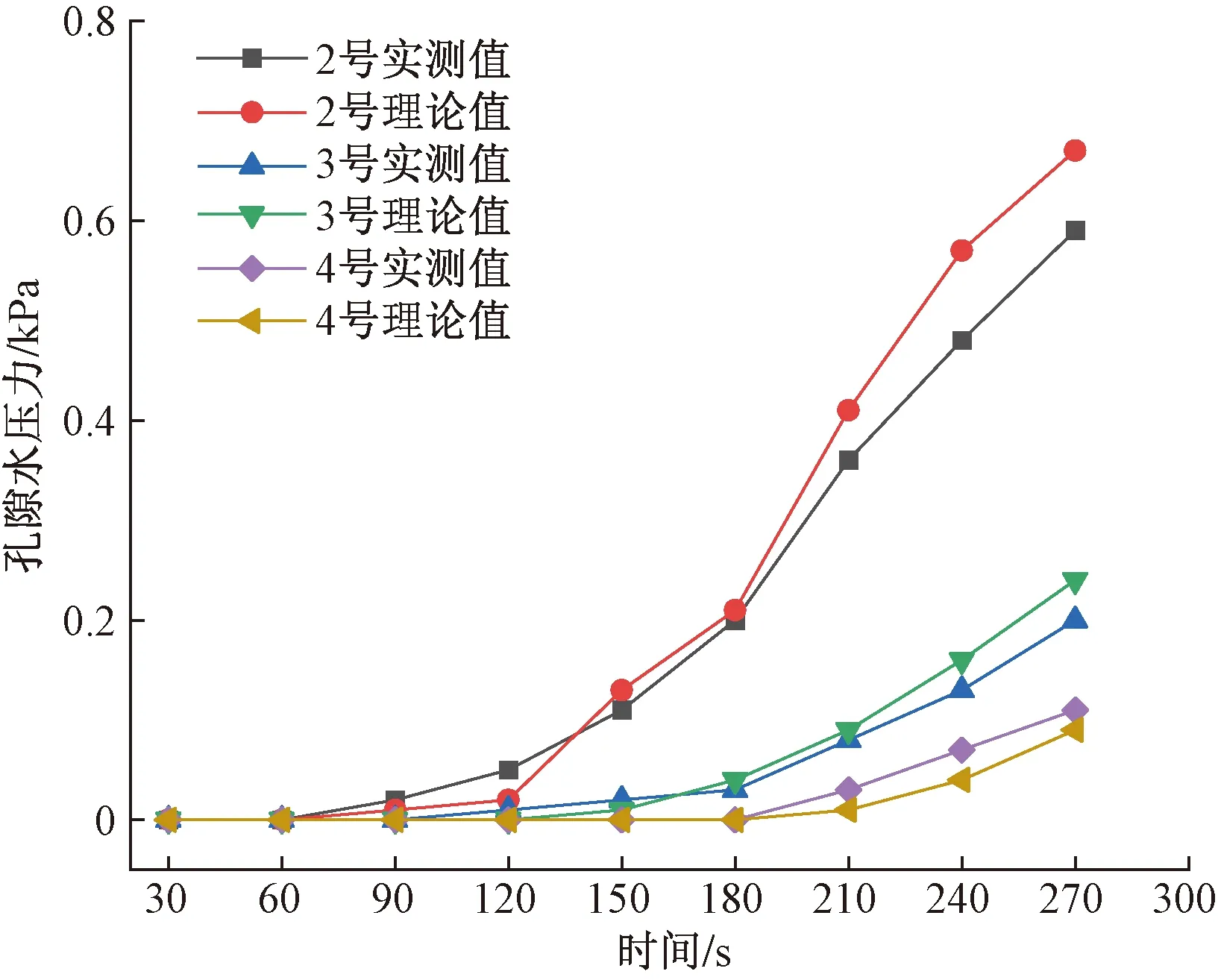
图12 蓄水期孔压计算结果Fig.12 Calculation results of pore water pressure in impoundment period

(1)根据堰塞坝溃口演化特征，可将的溃决过程分为3个阶段：坡面侵蚀阶段(阶段Ⅰ)、溯源陡坎侵蚀阶段(阶段Ⅱ)、粗化再平衡阶段(阶段Ⅲ)，其中，阶段Ⅱ发展最为剧烈，出现溃决洪峰流量，为来水流量的4.8倍。

(2)堰塞坝溃决过程中各测点孔隙水压力的变化过程均呈现先增后减的变化趋势，并存在明显的滞后现象；堰塞坝溃决过程中上游坝体孔隙水压力较下游明显增大，敏感程度也更高。

(3)堰塞坝溃决过程中左(为溃口一侧)右两侧的孔隙水压力呈“左小右大”的变化趋势，二者差值随溃口发展速率的加快而增加，即溃口演化过程对坝体孔隙水压力(或渗流)起着决定性作用。

(4)采用非稳定二维渗流微分方程对蓄水期坝体孔隙水压力进行计算，发现计算值与实测值间虽然存在一定差别，但整体变化趋势类同，仍然存在一定的参考价值；而对于如何进一步实现对溃口发展过程中孔压的准确计算，则需要在对溃口演化过程做出更深层次的定量描述的基础上，采用非稳定三维渗流微分方程对现有数值模型进行求解。