初始孔压非均布条件下散体材料桩复合地基固结理论研究

张玉国，岳 峰，谢康和

（1. 中原工学院 建筑工程学院，郑州 450007；2. 中原工学院 现代教育技术中心，郑州 450007；3. 浙江大学 岩土工程研究所，杭州 310027）

1 引 言

国内外现有的散体材料桩复合地基固结解析理论均是建立在初始孔压均布的基础之上[1－15]，而在实际工程中，外部荷载并不是连续的均布荷载，其在地基中产生的附加应力是沿深度变化的。因此，开展初始孔压非均布条件下散体材料桩复合地基固结理论的研究，既有理论意义更有实际价值。

2 数学模型

2.1 计算简图与基本假定

图1为考虑初始孔压非均布的散体材料桩复合地基固结计算简图。H为软黏土层的厚度，、分别为地基土体水平向及竖向渗透系数；为桩体周围扰动区水平向渗透系数，为桩体内竖向渗流时桩体渗透系数，、分别为土体和桩体的压缩模量，、、分别为散体材料桩半径、扰动区半径和排水影响区半径，q为一次瞬时施加的外部荷载，其引起的沿深度方向分布的非均布初始孔隙水压力(z)，具体见图2，r、z为径向及竖向坐标，设地基的排水条件均为PTIB，即顶面透水、底面不透水。

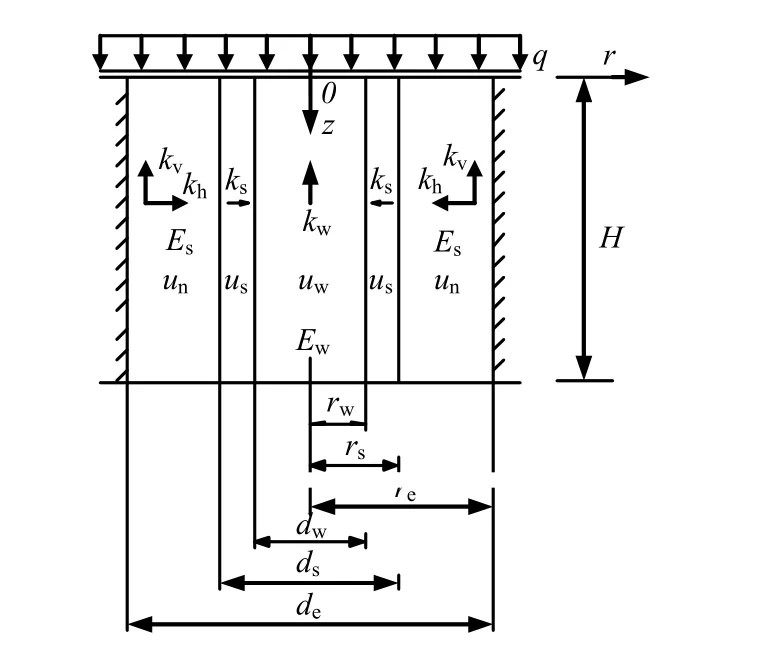
图1 计算简图Fig.1 Sketch of simplified computation model

图2 初始孔压分布Fig.2 Nonuniform distribution of initial excess pore water pressure along depth

基本假定如下：

①等应变条件成立，即同一深度处地基土体和桩体的竖向变形相等；②忽略桩体内的径向渗流；③扰动区与未扰动区土体除径向渗透系数不同外，其他性质相同；④土体中水的渗流服从Darcy定律；⑤任一深度z处从土体中沿桩周流入桩体的水量等于桩体中向上水流的增量；⑥荷载一次瞬时施加，引起的初始孔压沿深度方向是非均匀分布的。

2.2 固结方程及求解条件

对于散体材料桩复合地基，由平衡条件和基本假定，得：

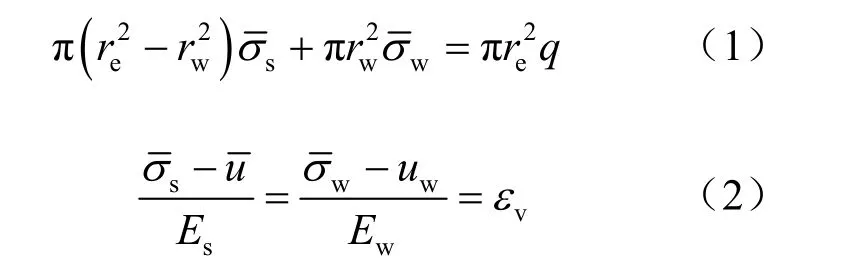
由式(1)、(2)，得：

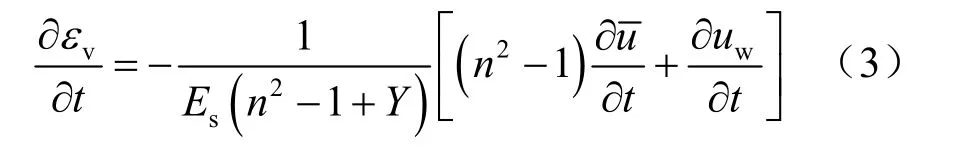
Barron等应变条件下基本固结方程为

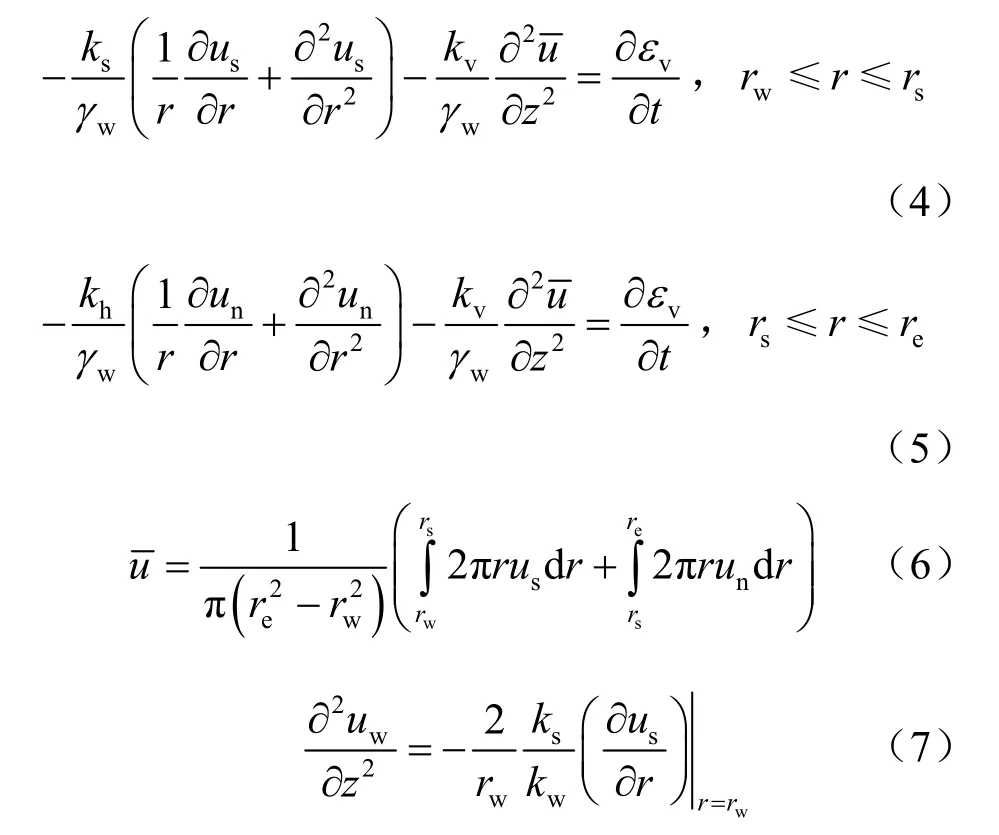
边界条件：

初始条件：

式中：un、us、uw分别为土体未扰动区、扰动区和桩体内任一点的孔压；分别为土体和散体材料桩体中任一深度处的平均总应力；为土体中任一深度处的平均孔压和竖向应变；n=re/rw； s=rs/rw； Y=Ew/Es；pT、pB分别为土层顶面和底面的初始孔压值，当 pT= pB= p0时，初始孔压均布，如图 2(a)所示；当pT=0时，初始孔压沿深度呈正三角形分布，如图 2(b)所示；当pB= 0时，初始孔压呈倒三角形分布，如图 2(c)所示；当 pT≠pB≠ 0时，初始孔压呈梯形分布，如图2(d)所示。

3 方程求解

参照文献[12]有关散体材料桩复合地基固结方程的求解方法，根据方程式(4)～(7)和边界条件式(8)～(10)，可求得：

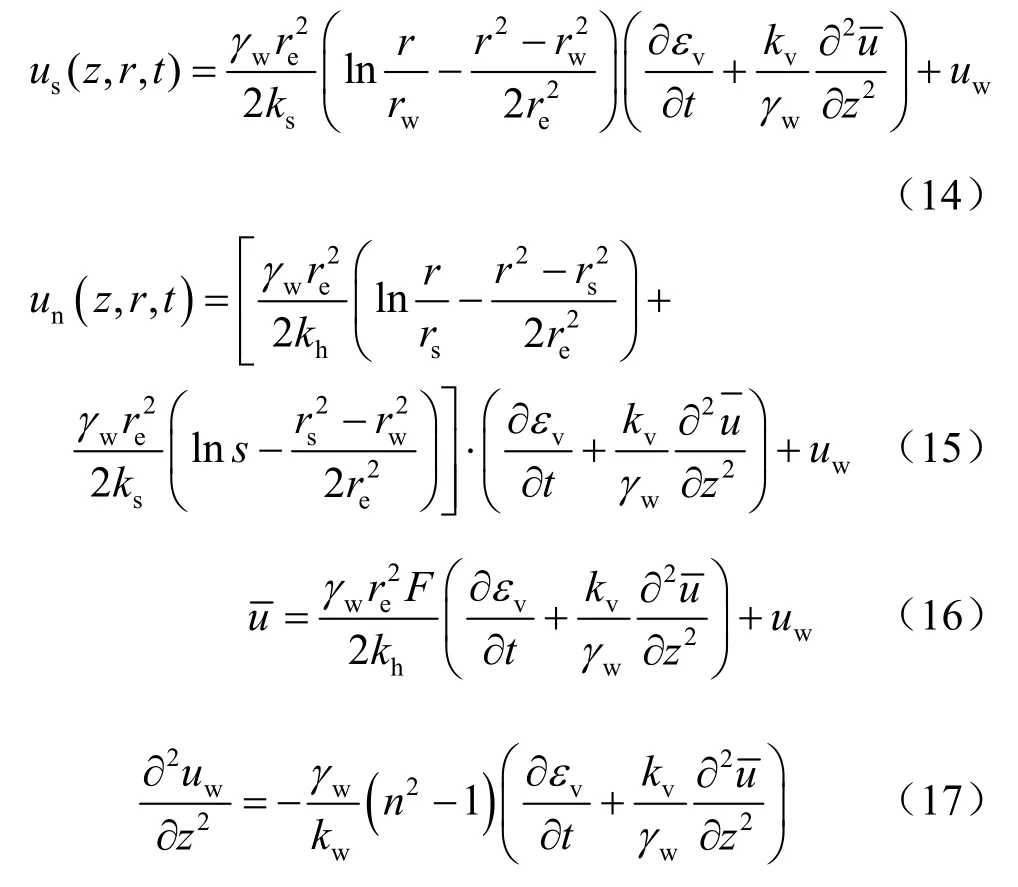
由式(16)和(17)得：

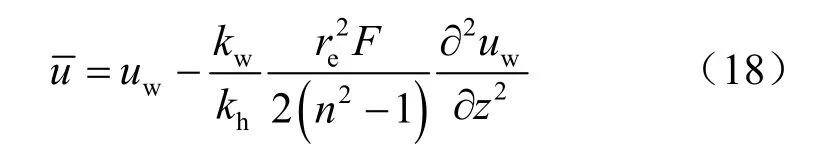
联立式(3)、(16)和(17)，有：

对式(21)采用分离变量法求解，令uw= Zw(z)T(t)，利用式(18)和边界条件式（11）～（12），可求得：

根据初始条件式(13)和式(22)，并利用三角函数正交性，可以求得：

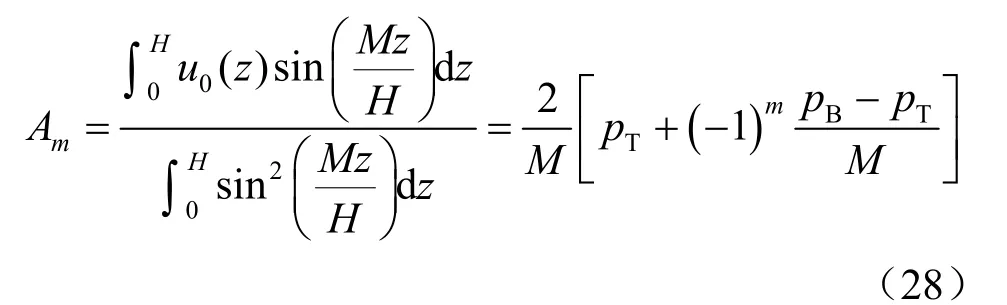
所以，有

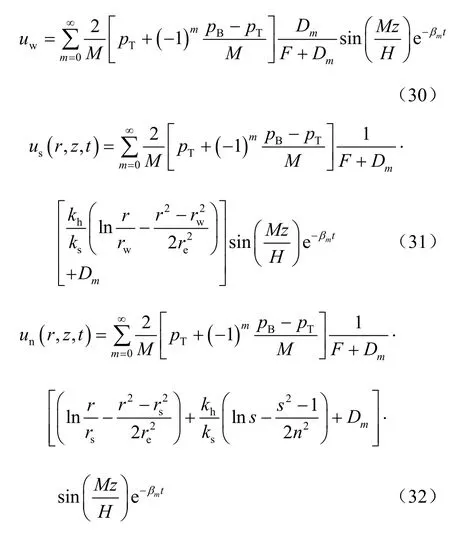
现在，可以求得复合地基任一深度处的固结度和总平均固结度如下：

根据初始孔压u0(z)分布情况（见图 2），下面将进一步给出各特殊情况下的复合地基平均孔压和平均固结度表达式。

情况1：初始孔压矩形分布，见图2(a)：

此时， pB=pT=p0，则式(29)和式(34)退化为文献[12]给出的一次瞬时加载初始孔压均布的散体材料桩复合地基固结解析解，即

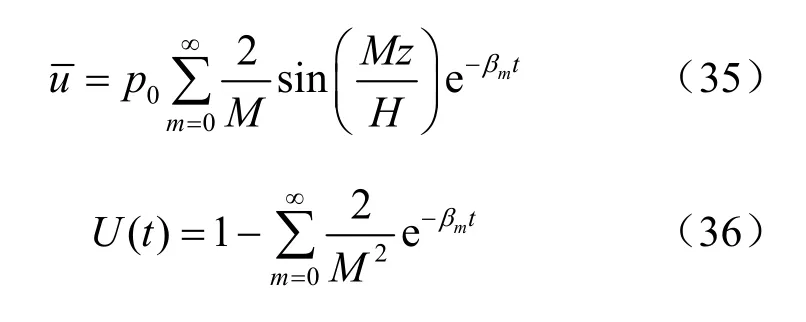
情况 2：初始孔压正三角形分布，见图 2(b)，此时，pT=0，则由式(29)和式(34)得

情况 3：初始孔压倒三角形分布，见图 2(c)，此时，pB=0，同样，由式(29)和式(34)得

至此，给出了关于初始孔压非均布条件下的（仅考竖向渗流）散体材料桩复合地基固结解析解。现有解[12]为本文解的特例。

4 计算与分析

基于上述解，由式(29)～(41)可以看出，考虑初始孔压非均布时散体材料桩复合地基固结主要受以下无量纲化参数影响：n、s、H /dw、kh/kv、kh/ks、kh/ kw、 Ew/Es和 pB/pT。根据本文解编制计算程序，对固结规律进行研究分析。图3～12为计算结果，图中Tezerghi曲线即为根据Tezerghi解绘制的曲线，代表了桩体直径为 0、无水平向渗流和土体压缩模量均一时（或即天然地基）的固结曲线，其余曲线的参数详见图中文字。

图3～8反映的是基于各参数对复合地基固结过程的影响。

从图3可见，在单面排水条件下，初始（或起始）孔压为正三角形分布时固结最慢，初始孔压为矩形分布（即均布）时固结较快，初始孔压为倒三角形分布时固结最快。

图4给出的是 pB/pT对固结过程的影响曲线。从中可见： pB/pT比值越小，固结越快。

图5反映的是 kh/ks对固结过程的影响。图 6为 kh/ks和n对固结过程的影响曲线图。图7是n对固结过程的影响曲线图。这些图中曲线显示，kh/ks和n值越小，固结就越快。

从图8所示的Y（即 Ew/Es）对固结过程的影响曲线可见，桩体压缩模量越大，固结越快。

图9～12展现了初始（或起始）孔压不同分布时地基中超静孔压的分布情况。

从图9、10所示的初始孔压均布和正三角形分布条件下的超静孔压等时线，由图可知，超静孔压随着Tv值的增大而逐渐消散，在固结过程中，地基底部孔压总是最大值。

图3 对应于不同起始（或初始）孔压分布的固结曲线Fig.3 The consolidation curves corresponding to different initial excess pore water pressure distributions

图4 pB /pT变化对固结过程的影响曲线Fig.4 The influence of pB /pT on consolidation process

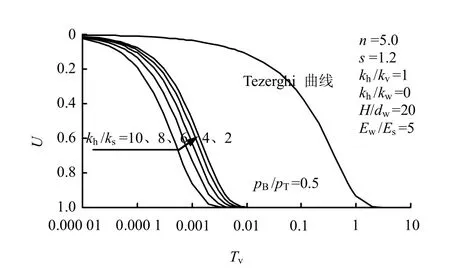
图5 kh /ks对固结过程的影响曲线Fig.5 The influence of kh /ks on consolidation process

图6 kh /ks和n对固结过程的影响曲线Fig.6 The influence of kh /ks and n on consolidation process

图7 n对固结过程的影响曲线Fig.7 The influence of n on consolidation process

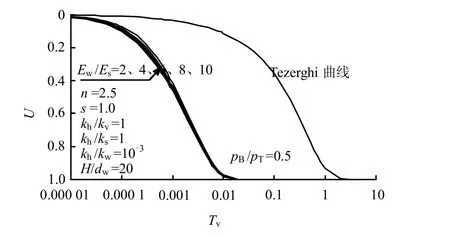
图8 Ew /Es对固结过程的影响曲线Fig.8 The influence of Ew /Es on consolidation process

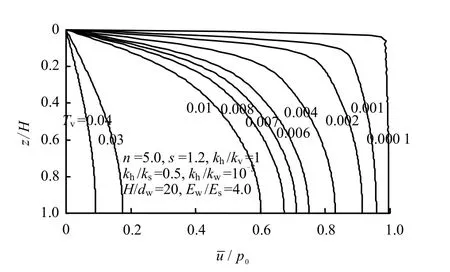
图9 初始孔压均布条件下的超静孔压等时线Fig.9 The excess pore pressure isochrones under the uniform distribution of initial excess pore water pressure

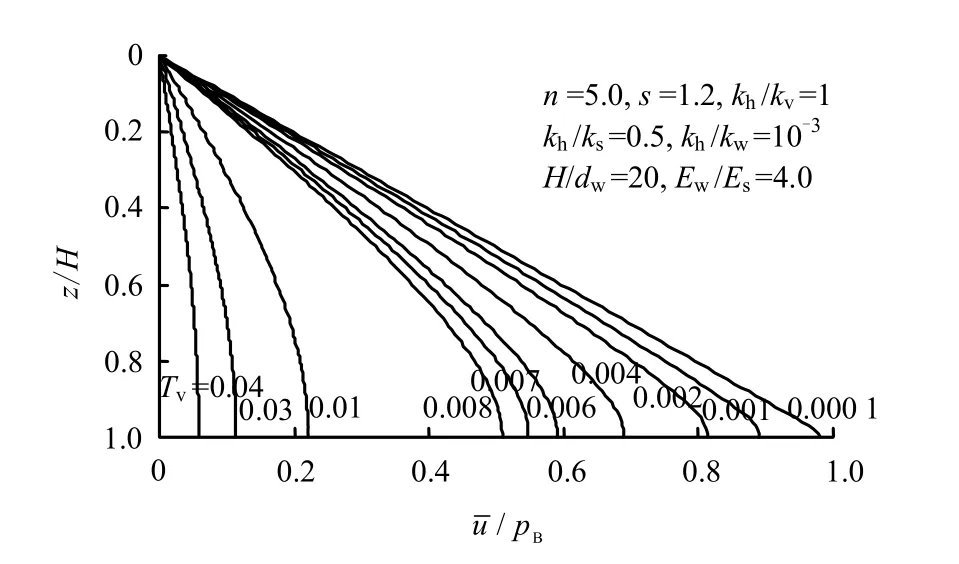
图10 初始孔压正三角形分布条件下的超静孔压等时线Fig.10 The excess pore pressure isochrones under the triangle distribution of initial excess pore water pressure

图11 初始孔压倒三角形分布条件下的超静孔压等时线Fig.11 The excess pore pressure isochrones under the inverted triangle distribution of initial excess pore water pressure

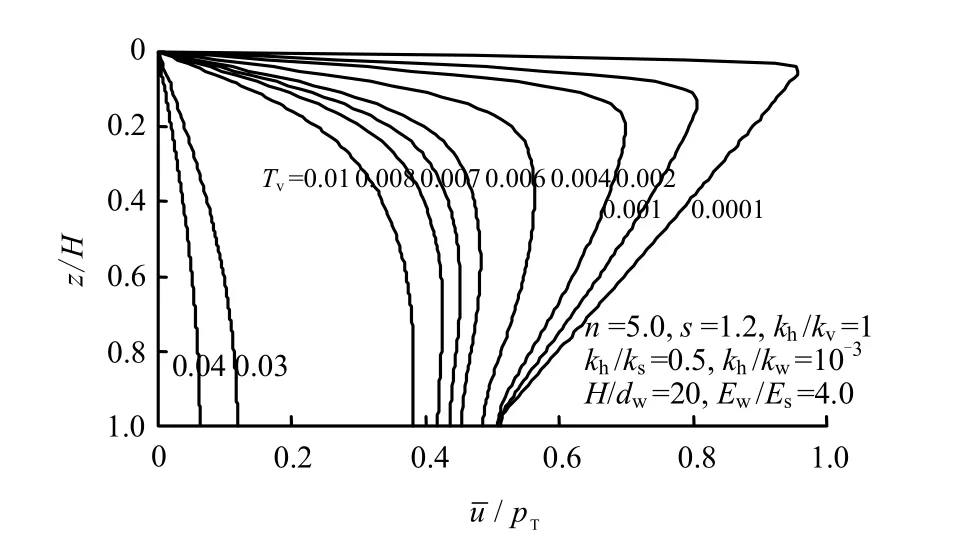
图12 初始孔压梯形分布条件下的超静孔压等时线( pB /pT =0.5)Fig.12 The excess pore pressure isochrones under the trapezoidal distribution of initial excess pore water pressure ( pB /pT =0.5)

根据图 11中初始孔压倒三角形分布条件下的超静孔压等时线，分析可知，Tv值越大，超静孔压等时线越平缓，且最大孔压值的位置由地基顶部向底部逐渐转移；在固结过程中，底部孔压值的变化呈现从小变大、再变小的特点。

图12为初始孔压梯形(pBpT= 0.5)分布条件下的超静孔压等时线。通过比较图9、11和12可知，图 12中的超静孔压变化规律与初始孔压倒三角形分布条件下的超静孔压变化规律相类似；另外，随着 pBpT的增大，特别是 pBpT趋近于1时，地基底部孔压“从小变大、再变小”这一变化特点会消失。

5 结 论

（1）本文求得了初始孔压非均布条件下仅考虑桩体内竖向渗流的散体材料桩复合地基固结解。

（2）在单面排水条件下，初始孔压为正三角形分布时固结最慢，矩形分布（均布）时固结较快，倒三角形分布时固结最快； pBpT、kh/ks和n值越小，固结越快；桩体压缩模量越大，固结越快。

（3）初始孔压均布和正三角形分布时，超静孔压随Tv值的增大而逐渐消散，在固结过程中地基底部孔压总是最大值；初始孔压倒三角形和梯形（ pBpT= 0.5）分布时，Tv值越大，孔压等时线越平缓，孔压最大值位置由地基顶部向底部转移，在固结过程中底部孔压的变化呈现“从小变大、再变小”的特点；当初始孔压为梯形分布，同时， pBpT值趋近于1时，底部孔压的这一变化特点会消失。

[1]BALAAM N P, BOOKER J R. Analysis of rigid rafts supported by granular piles[J]. International Journal for Numerical Analytical Methods in Geomechanics, 1981,(5): 379－403.

[2]XIE K H, XU Y, HU A F. Study on consolidation of composite foundation under highway[C]//Proc. of 12th Asian Regional Conf. on Soil Mechanics and Geotechnical Engrg.. Singapore: [s. n.]: 2003.

[3]王瑞春. 竖井地基和散体材料桩复合地基固结解析研究[D]. 杭州: 浙江大学, 2001.

[4]张玉国. 散体材料桩复合地基固结理论研究[D]. 杭州:浙江大学, 2005.

[5]谢康和. 砂井地基: 固结理论、数值分析与优化设计[D].杭州: 浙江大学, 1987.

[6]WANG Xu-sheng, JIU J J. Analysis of soil consolidation by vertical drains with double porosity model[J].International Journal for Numerical and Analytical Methods in Geomechanics, 2004, (28): 1385－1400.

[7]张玉国, 谢康和, 应宏伟, 等. 双面半透水边界的散体材料桩复合地基固结分析[J]. 岩土工程学报, 2005,27(3): 304－307.ZHANG Yu-guo, XIE Kang-he, YING Hong-wei, et al.Consolidation analysis of composite foundation of granular columns with impeded boundaries[J]. Chinese Journal of Geotechnical Engineering, 2005, 27(3): 304－307.

[8]谢康和. 双层地基一维固结理论与应用[J]. 岩土工程学报, 1994, 16(5): 24－35.XIE Kang-he. Theory of one dimensional consolidation of double-layered ground and its applications[J]. Chinese Journal of Geotechnical Engineering, 1994, 16(5): 24－35.

[9]谢康和, 潘秋元. 变荷载下任意层地基一维固结理论[J]. 岩土工程学报, 1995, 17(5): 80－85.XIE Kang-he, PAN Qiu-yuan. One-dimensional consolidation theory of layered systems under time-dependent loading[J]. Chinese Journal of Geotechnical Engineering, 1995, 17(5): 80－85.

[10]蒋军, 陈龙珠. 长期循环荷载作用下粘土的一维沉降[J]. 岩土工程学报, 2001, 23(3): 366－369.JIANG Jun, CHEN Long-zhu. One-dimensional settlement due to long-term cyclic loading[J]. Chinese Journal of Geotechnical Engineering, 2001, 23(3): 366－369.

[11]王瑞春, 谢康和. 变荷载竖向排水井地基粘弹性固结沉降解析解[J]. 土木工程学报, 2001, 34(6): 93－99.WANG Rui-chun, XIE Kang-he. Analytical solutions for viscoelastic consolidation by vertical drains under time-dependent loading[J]. China Civil Engineering Journal, 2001, 34(6): 93－99.

[12]TANG X W. A study for consolidation of ground with vertical drain system[D]. Japan: Saga University, 1998.

[13]XIE K H, GAO P, XIE X Y. Consolidation theory for soft clays reinforced by cement or granular columns[C]//Proceedings of Computer Method and Advances in Geomechanics. Rotterdam: Balkerma, 2001:1263－1268.

[14]ZHANG Y G, XIE K H, WANG Z. Consolidation analysis of composite ground improved by granular columns considering variation of permeability coefficient of soil[C]//Proceedings of Ground Modification and Seismic Mitigation. [S. l.]: [s. n], 2006.

[15]张玉国, 海然, 谢康和. 变荷载下散体材料桩复合地基固结研究[J]. 岩土工程学报, 2009, 31(6): 939－945.ZHANG Yu-guo, HAI Ran, XIE Kang-he. Consolidation of composite ground with granular columns under time-dependent loading[J]. Chinese Journal of Geotechnical Engineering, 2009, 31(6): 939－945.