典型堤防溃口水力特性的试验研究

李晓晨，马洪福，刘明潇，董明家

(1.华北水利水电大学水利学院，郑州 450046；2.华北水利水电大学水力学及河流研究所，郑州 450046；3.水发规划设计有限公司，济南 250100)

我国是一个地域广阔、洪涝灾害频生的国家。洪涝灾害引发的大坝、堤防溃决严重影响了当地的正常经济发展，严重威胁了人民群众的正常生产生活和生命财产安全。例如在过去将近150年中，黄河大堤发生决口96次[1]。黄河中下游地区，在历史上深受堤防溃口带来的巨大灾难。堤防作为约束河流的最重要工程手段，被广泛用于保护河流两岸的居民和工农业生产。然而由于技术和自然地理条件限制，并不能保证堤防在任何上游来流流量下的绝对安全。当上游来流超过堤防的抵御能力，或在汛期抢险不当，都会导致堤防出现溃口[2]。因此，研究溃堤水流规律，会对溃堤灾害的预防和处理提供重要的参考价值。

堤防溃口附近的水流运动规律极其复杂，在模型试验方面，国内外学者针对溃口的水力模型试验展开了诸多研究。SOARES-FRAZO等[3]、BELLOS等[4]分别进行的水力模型实验，揭示了洪水波在不同条件下的流动规律。孙芦忠等[5]通过分析溃口口门处水力学参数的变化规律得出了计算口门流量的经验公式；陆灵威[6]则通过物理模型实验，模拟了溃堤发生时河道和洪泛区内水流过程。张晓雷等[7]进行了堤漫滩洪水的概化模型试验，模拟了生产堤溃决后主槽内的水位变化及不同程度漫滩洪水的传播过程。但溃口的堵复工作多在溃口中后期开展，针对溃口中后期口门和洪泛区的水流运动规律仍需要进一步研究。

根据堤防溃口在中后期的水流变化特性，本文基于典型溃口边界条件进行了水力模型试验，分析探讨各特征参数之间的相互依存关系和溃口中后期的水力特征值变化规律；并针对堤防溃口发生时溃口和洪泛区的复杂流场，对溃口处水位-流量关系、堤后主流流速和运行轨迹、溃口水流动量变化规律等进行了实验研究和总结分析，以期对堤防溃口的堵复工作提供理论依据。

1 典型堤防溃口的选择

在进行堤防溃口发生机理研究和开展堵口技术研究时，确定典型堤防溃口水力边界特征值是整个研究的重要基础和前提。根据马洪福[8]等的研究，其利用聚类分析方法建立了溃口水力边界特征值间相关关系，同时使用概率统计手段研究了溃口水力特征值的分布，提出了适用于土质堤防的典型溃口参数：溃口宽多在20～100 m，宽深比处于3～8区间的分布频率为55%。口门水头多在4～12 m，口门流速多在2～8 m/s，溃口弗劳德数处于0.4～0.8区间的分布频率为60%。

2 基于VDMS的溃口模型试验设计

2.1 模型设计

依据相似原理设计了概化溃口正态物理模型，设计模型比尺为1∶50，其平面布置如图1所示。溃口口门为倒等腰梯形，顶宽120 cm，底宽72 cm，边坡系数为1。堤顶和堤坡表面为水泥砂浆抹砌，高24 cm，上、下断堤头各长300 cm，迎水和背水坡坡比均为1∶3。模型最大设计流量为110 L/s，最大流速为1.13 m/s。本文建立的溃口物理模型对应的溃口原型宽度60 m，宽深比为5，口门轴线处水头在1.25～7.1 m之间，口门最大流速8 m/s，最大流量1 944.54 m3/s，试验中溃口区弗劳德数涵盖了0.3～1.4的范围。溃口模型尺寸的选取体现了江河堤岸土石类堤防，其溃口后期经过不断淘刷大多具有宽度大于水深的宽浅特点。选取流速、流量分布范围也体现了溃口中后期多为缓流的流态，因此本文的研究对于土石类堤坝溃口具有较好代表性。

图1 典型堤防溃口水力模型布置平面图(高程：m)Fig.1 Layout plan of hydraulic model of typical dyke breach

根据张晓雷[7]等的研究，溃堤后漫滩水流基本沿溃口横向演进，洪水波以溃口为中心近似呈对称式椭圆形分布向四周扩散，其长轴轴线略偏向下游。其实验成果说明溃堤前期漫滩水流从溃口流出时主流扩散角约为30°～45°，而中后期滩区进流较小，水位基本稳定。本文模型模拟滩区宽672 cm，长300 cm，在模型的正向和两侧边墙设计了排水口和闸门，正向尾水口宽4 m，两侧排水口各宽1 m。正向尾水口使得溃口前期漫滩水流在主流保持在左右各约35°扩散角的状态下顺畅流出，通过控制两侧排水门的开合可以模拟溃口后期漫滩洪水在溃口下游洪泛区的左右扩散。

概化水槽试验采用循环式供水系统，由供水、输水和回水3大部分组成，包括试验室地下水库、输水管路、模型前池、尾水池等，可满足模型试验流量及退水要求。利用变频水泵、E-MAG电磁流量计、阀门及输水管道系统，实现了模型区的供水往复、循环利用。在模型河道上游和堤外滩区均布置了0.1 mm级水位测针，并使用VDMS(Velocity Distribution Measuring System,VDMS)技术进行非接触式流场测量，两个摄像机位于溃口上方6 m，镜头纵轴垂直于水平面，实际操作时保证倾斜误差控制在10°以内[9]，如图2所示。采用的示踪粒子为白色扁圆型聚丙烯颗粒，直径20 mm，重量2 g，密度约等于水。

2.2 试验方案的选定

本文选取溃口洪峰过后，上游河道来流量不变的溃口中后期进行试验。试验中，使用水泵变频器、电子阀门和电磁流量计调整流量，使用固定在河道上游和堤后滩区的0.1 mm级水位测针量测上游和滩区水位，使用毫米级测尺测量溃口轴线水深H，使用旋桨式红外流速仪测量溃口口门轴线流速v。通过VDMS系统观测流场、断面流速分布以及多个测点的流速矢量变化过程，实验工况如表1所示。其中C-1～C-10工况溃口流量逐渐递减，以研究溃口水力参数变化规律。C-11～C15工况则主要研究在急、缓流条件下的流场表面流速分布。

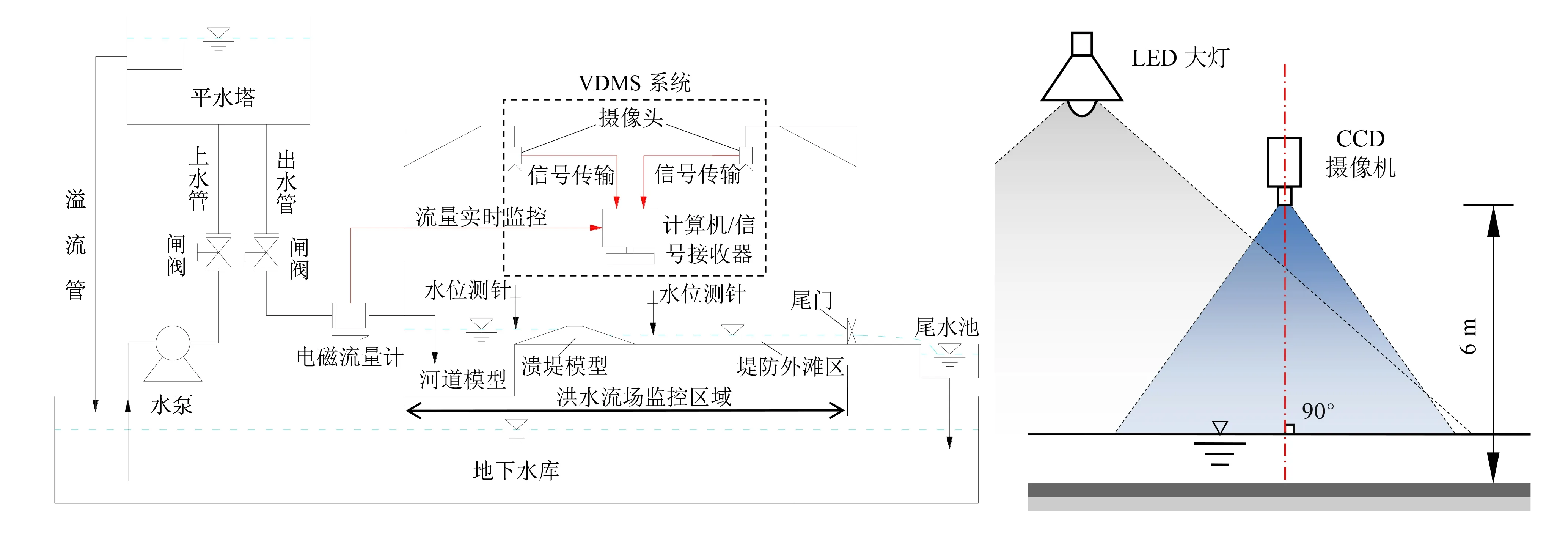
图2 模型水循环和VDMS系统Fig.2 Model water circulating and VDMS system

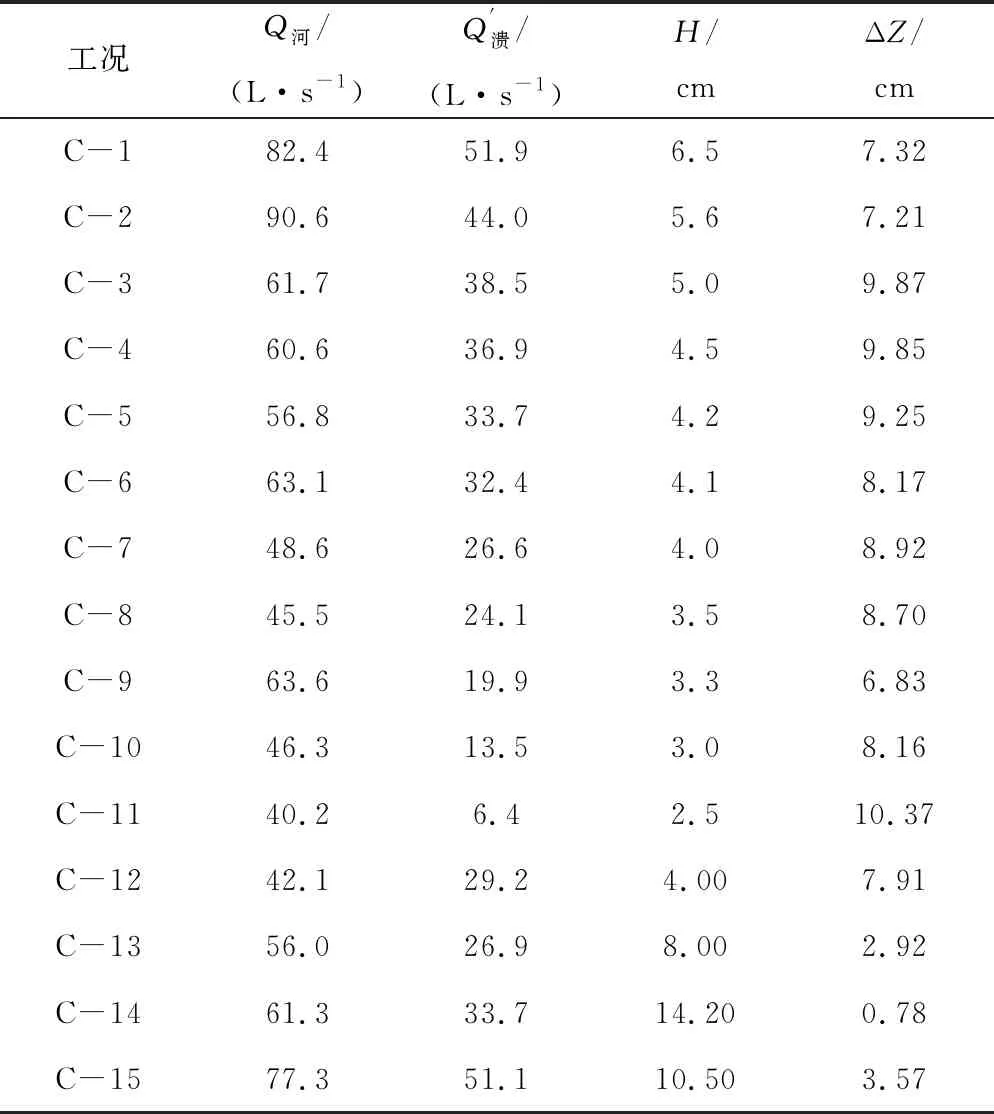
表1 试验工况Tab.1 Test case

3 溃口水力特性的试验成果分析

堤防溃口的中后期阶段，堤后滩区的水位不断上涨，溃口内外水位差逐渐缩小，将会导致溃口流量、流速、水深等水力学参数的变化。在实验时，每个工况初始时3个尾水闸门全部处于开启状态，随着试验的进行尾门逐渐关闭，模拟溃口中期到后期滩区壅水的变化过程，确保水力学试验的可重复性，极大提高试验成果的可信度。

3.1 溃口流场特性分析

选取五组流场成果(C-11～C-15)进行流场流速分布的重点分析，从表2中可以看出，溃口对应原型流速在2～6 m/s之间，基本涉及了常见的溃口流速范围；涉及了2种急流工况和3种缓流工况，分别用以模拟溃口发生中期和后期的溃口流态变化，表中给出了相应的弗劳德数Fr。

表2 溃口模型流场试验工况Tab.2 Flow field test case of the breaching model

对比工况C-11和C-15，探究了相同口门流速而其他水力参数不同的情况下的流场分布。为了保持两者相同的溃口轴线流速，设置了不同的流量和堤内外水头差，实现了相同流速下急流和缓流两种流态的溃口区水流运动状态对比。如图3、图4，虽然两工况的溃口流量比接近8，但是口门附近流速分布规律基本相同：因溃口对河道水流起到了分流作用，溃口上下游的河道水流流速有明显变化；河道水流进入堤防溃口时流速指向下断堤头，在受到下断堤头阻拦和引导后，才在溃口内形成较为平顺的高速水流；溃口下断堤头附近产生漩涡，出现反向流速汇入溃口。但两工况因分属急、缓流，弗劳德数比值接近2，流场细节仍有较大差异。工况C-11在溃口下游出现了水跃，流场波动剧烈，但因溃口流量较小，洪泛区内洪水主流两侧形成顺时针方向漩涡，漩涡对应原型流速最大仅为0.60 m/s；而工况C-15原型溃口流量高达918 m3/s，溃口处为缓流，流场分布较为有序，洪泛区内的左侧涡流流动方向为逆时针，与工况C-11相反。

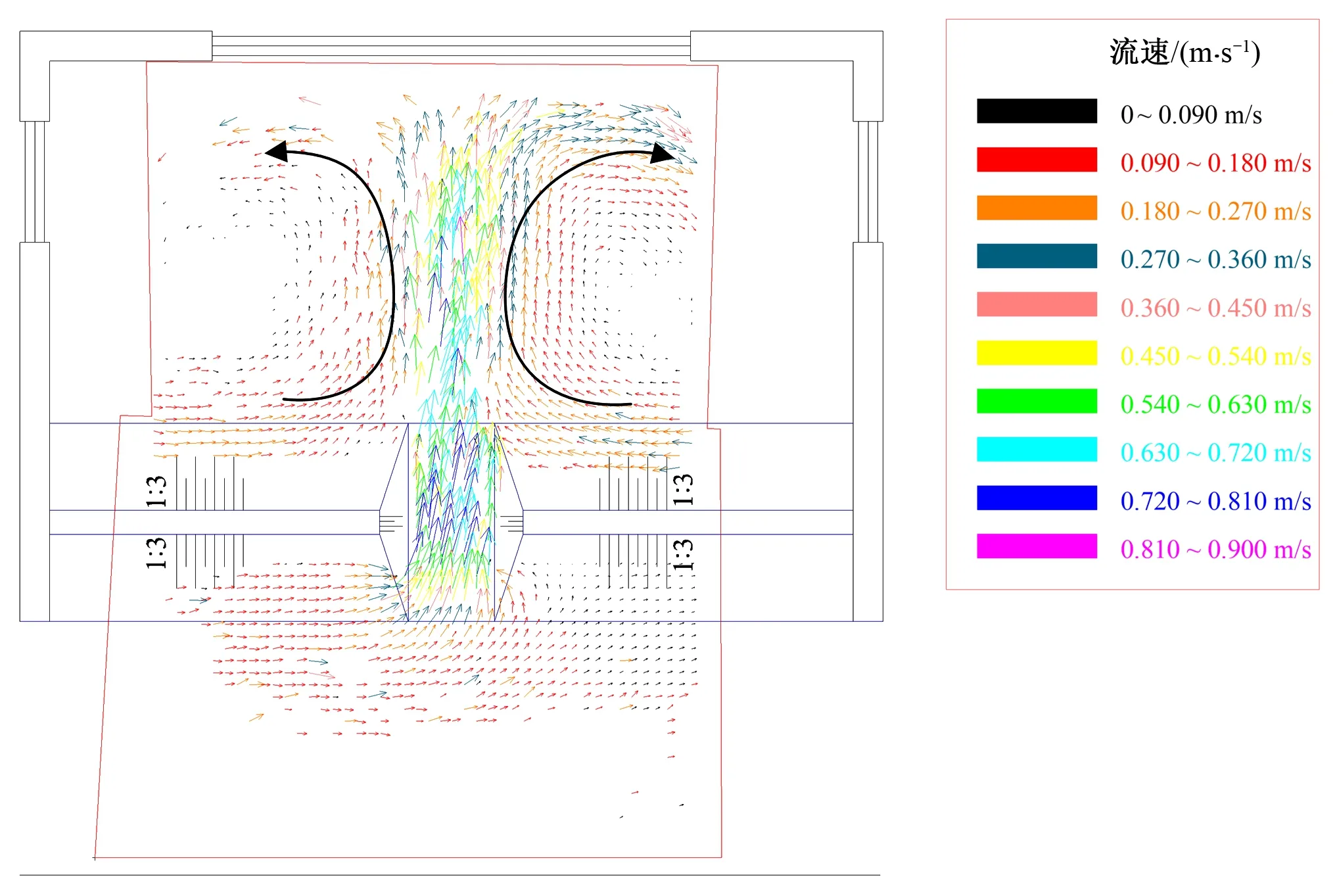
图3 工况C-15溃口流场Fig.3 Flow field diagram of case C-15

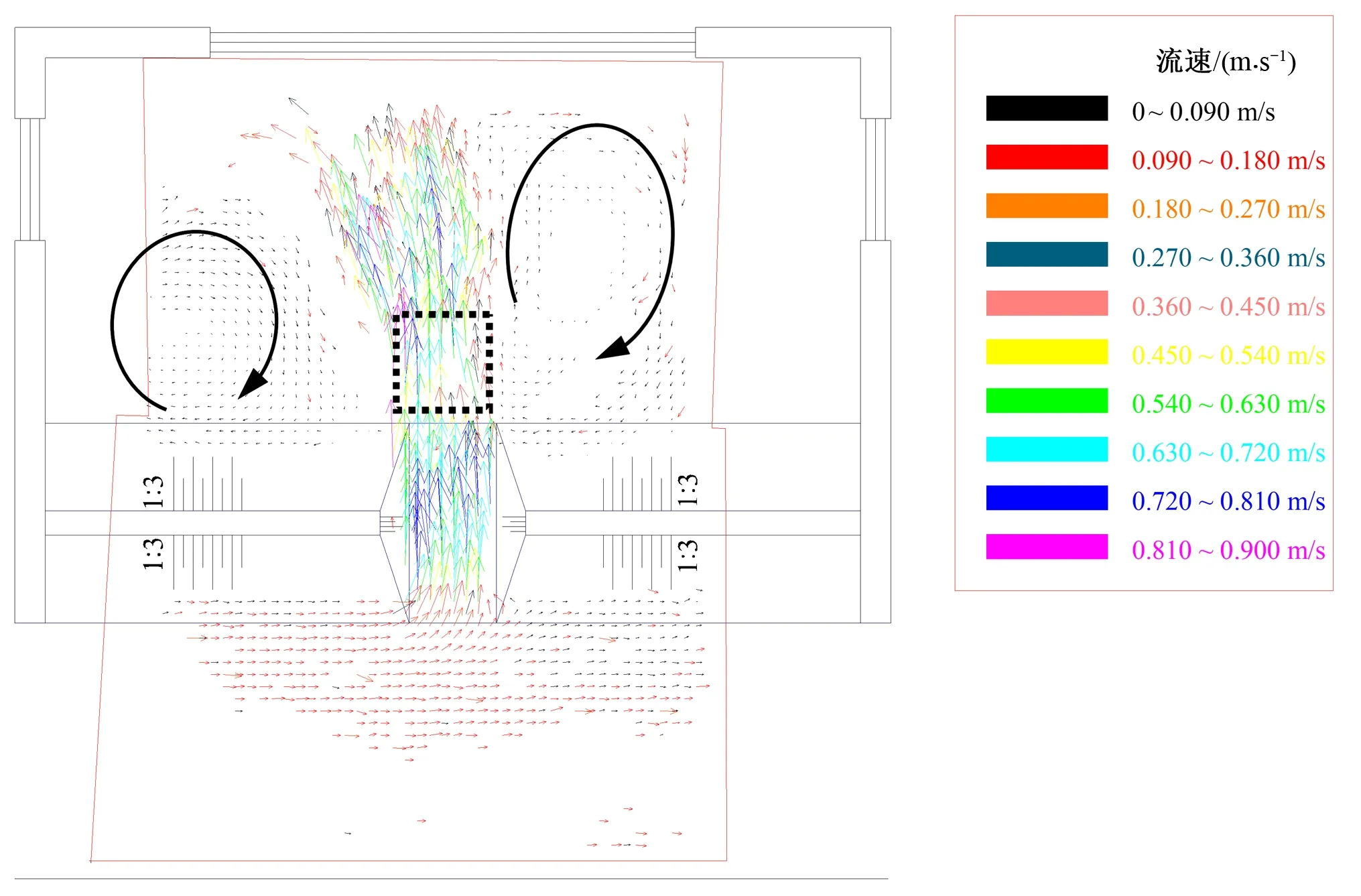
图4 工况C-11溃口流场Fig.4 Flow field diagram of case C-11

工况C-12和工况C-11溃口轴线流速都在0.70 m/s以上，原型流速在6～8 m/s以上，水流动能较大，弗劳德数大于1，属于堤防溃口中高速水流的范围。于是两工况在溃口下游都发生了水跃，跃后水面波动剧烈、流速分布紊乱，水跃具体位置在如图虚线框内，如图5。两工况在洪泛区内因主流集中且摆动较大，占据了大部分溃口流量和水流动能，所以洪泛区内影响流速分布的主要因素为主流的水跃和摆动。反映在洪泛区内具体流场分布上，即为主流左侧漩涡并没有按照常见水力学规律出现与右侧镜像对称的逆时针漩涡，而是两工况主流两侧均为顺时针漩涡。

图5 工况C-12溃口流场Fig.5 Flow field diagram of case C-12

图6 工况C-13溃口流场Fig.6 Flow field diagram of case C-13

工况C-13和工况C-14模拟溃口后期溃口内外水面坡降和溃口流速逐渐减小、水流动能降低、溃口区域流速分布逐渐稳定的情况。如图6，溃口内下断堤头附近高流速分布密集，是模型区域内高流速集中的区域，断堤头坡面附近最大模型流速达0.40 m/s，存在堤防被冲蚀掏空的隐患。因处于溃口后期，两工况洪泛区内流场分布较为均匀，主流两侧涡流基本对称，漩涡区流速较为稳定，均在0.13 m/s以内。

3.2 溃口处水位～流量～流速的互补特性分析

在堤防溃口发展的中后期，随着洪泛区水位不断升高，在溃口尺寸基本不变的情况下，溃口口门处水深不断上升、流速不断减小，溃口仅保持较小的下泄流量，整体流态趋于平稳。针对溃口口门中轴线处的水位—流量变化情况，分别选取了工况C-1、2、4、7试验成果进行分析，其溃口的水位-流量和水位-流速关系如图7所示。

图7 典型溃口水位-流量和水位-流速关系曲线Fig.7 Typical water level-flow rate and water level-velocity relationship curve

分别对这4种工况进行拟合分析，当溃口水位升高时两者呈现不同的变化规律，流速以“先快后慢”的速率减小，流量以“先慢后快”的速率减小，反映在函数图像上即为两者拥有相反的凹凸性。根据水力模型倒梯形溃口的特征，溃口处的理论流量与无坎宽顶堰类似。当大河水位和溃口形式一定，下游水位逐渐抬高，会迫使溃口内水流转化为缓流形成淹没出流，减小了影响了溃口的过流能力。此时无坎宽顶堰计算理论流量的淹没系数σ同样随着下游水位的升高以“先慢后快”的速率减小[10]，与实测溃口流量-水位变化规律相同。总的来看，在同一工况中，水位-流量与水位-流速函数图像的凹凸性相反，表现出“互补性”。

3.3 溃口区水流功率特性分析

堤防溃口中后期溃口尺寸和形态基本稳定，堤防内外的水位差随着溃口处的不断泄流而逐渐减小。堤防溃口内外水位差直接影响溃口处的水头高度，决定了溃口流量、流速、水深等水力特征值的变化。本文对C-1到C-10共10个工况的试验成果进行了研究分析，选取水位差ΔZ为自变量，研究对溃口口门轴线处水深H、流速v和溃口流量Q溃的影响，其中流速v和流量Q溃,用水流功率P来表示，水流功率即单位时间流经溃口的某一横截面的水流(ρ=1 000 kg/m3)总动能，其表达式为[11]：

(1)

为提高试验成果的普适性，对单宽水流功率P/B、单宽水深H/B、单宽水位差ΔZ/B进行分析，根据实测数据，绘制单位特征值关系曲线图如图8所示。

图8 单宽水位差和单宽水流功率及单宽水深关系曲线图Fig.8 Curve diagram of relationship between single-wide water level difference, single-wide flow power and single-wide water depth

由图8(a)可以看到，以单宽水位差ΔZ/B等于0.07为分界线，在其左右侧水流功率呈现不同的变化规律。当单宽水位差由较大的初始值减小至约等于0.07时，其单宽水流功率基本保持不变。再由分界值0.07缩减至0的过程，单宽水流功率开始呈线性下降，当ΔZ/B下降至0时，单宽水流功率降至最小值2 W/s。溃口后期在口门形状和尺寸基本稳定的情况下，内外水位差与单宽水流功率呈现分段线性函数的关系，在单位水位差小于0.07时，单位水位差成为影响水流功率的主要因素之一。但只要溃口口门未被封堵，无论内外水位差如何变化，口门会一直保持下泄的流量。

由图8(b)可知，同样以单宽水位差ΔZ/B等于0.07为分界线，H/B在分界线两侧呈现不同的变化规律。左侧H/B大小基本不受水位差影响，右侧H/B的值随单位水位差减小呈现近似线性的增加，当口门水位差达到最小值时，口门水位达到最大值。在进行溃口堵复工作时，可以根据现场实测ΔZ/B值和试验得出的线性关系估测现场堤防溃决深度。

4 结 论

本文设计并开展了针对堤防溃口水力特性的模型试验研究，分别对溃口和洪泛区流场分布和水力学特征值相关关系进行了试验观测与分析探讨。

(1)根据溃口水力边界特征值间的相关关系，选择了具有一定的代表性的典型溃口形式及尺寸，设计了堤防溃口水力实验模型。

(2)针对溃口和洪泛区流场发展的中后期水力特性进行了研究，在溃口尺寸、形状基本不变的情况下，溃口口门区上游断堤头流速相对较小，下游断堤头受高速水流及漩涡的不断冲蚀淘刷，可能加剧堤防损坏。口门下游洪泛区主流两侧发生明显涡流，漩涡的流态和速率主要受溃口水流的影响，溃口为急流时洪泛区内主流集中且摆动较大，占据了大部分由溃口流出的水流动能，所以主流两侧漩涡流速较高，位置和尺度分布较为随机；溃口处为缓流时主流两侧漩涡基本对称，漩涡区流速较为稳定较为平稳。

(3)在溃口发展的后期，随着单宽水位差ΔZ/B的缩小，溃口单宽水流功率P/B以单宽水位差等于0.07为分界线，呈先平后降的发展趋势。而口门轴线水位呈不断升高的趋势，在单位水位差小于0.07时，单位口门水位与水位差呈现线性相关关系；溃口发展至中后期，上下游水头差减小，流态多呈缓流，仅保持了较小的下泄流量和较小的水流功率。

(4)在堤防溃口发展的中后期进行堵口工作时，溃口口门上游侧流速较下游侧小，适合在抛投物料时作为进占点。溃口区下断堤头处水面比降和流速大，冲刷强度高，是溃口堵复关注的重点；根据溃口区流场特性，断堤头裹护工作宜自上而下逐渐进行。

□