基于时间多重同步挤压W变换的高精度轴承故障诊断
和虎, 彭露, 赵金刚, 吴晓东, 郑洪越, 顾真齐, 陈辉*
(1.中国石化胜利油田分公司技术检测中心, 东营 257000; 2.成都理工大学数理学院, 成都 610059)
时频分析作为一种关键技术可以揭示非平稳信号的动态特征,被广泛应用于轴承故障诊断[1-3]。凡是有机械的地方就有轴承,如车辆、家电、抽油机等。在机械轴承故障诊断中,轴承是大型旋转机械中最关键的机械组件,也是最脆弱的机械部件,其缺陷会导致严重的机械问题和经济损失,因此如何从状态监测信号中识别这种故障显得尤为关键[4-6]。此外它自身就具有缺陷特征弱、外部噪声干扰强等特点,这都加大了识别的困难,因此发展高精度时频分析技术来检测这种故障特征则显得尤为重要[7-10]。研究者发现对于部分运行异常的机械,轴承缺陷会产生周期性的脉冲,这种脉冲可以被安装在机器上的状态监测(condition monitoring, CM)传感器捕捉到[11]。然而,由于缺陷信号幅值小,加之环境噪声的干扰,往往很难发现轴承早期缺陷产生的微弱脉冲分量[12]。此外,当信号中存在多个故障分量或在非平稳条件下采集信号时,有效地从CM信号中提取有效特征一直是轴承故障诊断和状态维修的重要研究课题之一[13-16]。
在时频分析技术的发展历程中,提高能量集中度是一个关键任务[3],因为集中的时频表示(time frequency analysis,TFR)更有助于轴承故障的准确诊断。目前经典的时频分析方法主要包括短时傅里叶变换(short-time Fourier transform,STFT)、连续小波变换(continuous wavelet transform,CWT)、S变换(S transform,ST)等,它们都属于线性变换,且都存在一定的适用性和不足,由于它们均基于窗函数,受海森堡测不准原理的限制,其时频谱的能量聚集性有限,难以准确地提取信号特征。因此,衍生出一类后处理方法:同步压缩变换(SST)及其改进版本,如基于CWT的SST[17]、基于STFT的SST[18]和高阶SST[19-21],由于其对非平稳信号能够产生高能量集中TFR,近年来受到广泛关注[20]。然而,上述大多数的SST技术隐含地假设分析信号表现为缓慢的时变特性,但实际轴承缺陷产生的类脉冲信号在很短的时间内发生,且频带很宽。当这类脉冲信号在较短的时间内发生快速的频率变化时,SST方法无法产生令人满意的TFR[21]。
针对SST不能较好处理脉冲信号的问题,He等[22]提出了时间重排同步挤压变换(TSST),在时间方向上对时频谱能量进行“挤压”,将其重新分配到真实的群延迟(group delay, GD)附近,因此其具备处理强时变信号的能力。TSST作为后处理方法可以得到较为集中的时频表征结果,但这种方法的时频分析结果很大程度上取决于通过经典时频分析方法获得的原始时频表征。
针对现有技术中的上述不足,为了提高CM信号的时频能量聚焦性以及准确捕获其中的脉冲分量,现提出一种高精度诊断轴承故障的时间多重同步挤压W变换(TMSSWT),首先采用W变换(使用一个具有围绕主频对称的频率权重的高斯窗函数)获取信号更为准确的原始时频表征结果,然后从时间方向对信号进行多次“挤压”,将时频能量重排至信号真实群延迟脊线上。以显著提高信号时频表征的能量聚焦性。最后采用模拟轴承信号对TMSSWT的时频谱进行时频包络谱的计算,得到最强时频振幅处所对应的频率,并在时频谱上提取对应的脉冲特性,分析结果表明该方法能够有效地用于轴承故障诊断。
1 TMSSWT方法理论
本文研究中考虑单分量频变信号x(ω)=A(ω)ejφ(ω),其中A(ω)、φ(ω)为信号的振幅和相位,j为虚数单位,ejφ(ω)相频特性函数。-φ′(ω)为群延迟(GD)。理想时频表征为ITFR(t,ω)=A(ω)ejφ(ω)δ[u+φ′(ω)],其中δ是脉冲函数,根据此式可知信号的时频特征应只出现在GD轨迹中。利用W变换可将信号扩展到TF域,W(t,f)的计算公式为
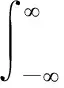
(1)
式(1)中:x(τ)为信号;t为时间中心;f为频率中心;g(τ-t,f;t)为高斯窗口函数;τ为时间变量;i为虚数单位,所述高斯窗口函数g(τ-t,f;t)为

(2)
式(2)中:k为标量因子,调节窗口函数形状;f0(t)为信号的时变主频;|Δf(t)|=|f0(t)-f|,所述时变主频f0(t)可根据瞬时频率的加权平均值计算,即
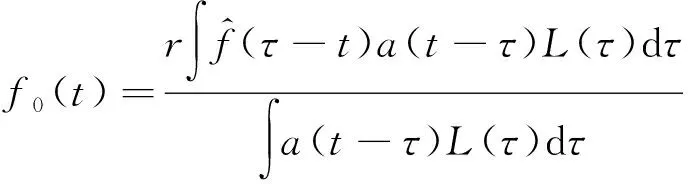
(3)
为提高W变换的能量聚焦性,TMSSWT首先根据W变换得到的时频谱的相位信息估计信号x在各个时频位置(t,f)处的群延迟t0(t,f)为
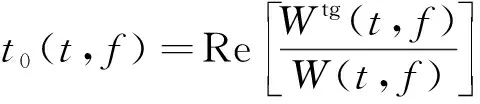
(4)
其(4)中:Wtg为在窗函数tg(t,f)下的W变换结果;Re表示取实部。
接下来,利用不动点迭代算法减少-φ′(ω)和t0(t,f)的误差[23],对于每一次迭代,二维GD估计越来越接近真实
表示新构造的N次迭代后各个时频位置(t,f)处的多重群延迟:
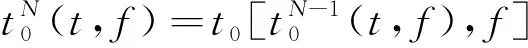
(5)
式(5)中:N为正整数,表示时间重排的阶数。当N=1时,有
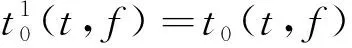
(6)
即一重群延迟,说明所述W变换得到的时频谱的相位信息估计信号x在各个时频位置(t,f)处的群延迟t0(t,f)。
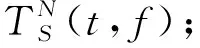

(7)
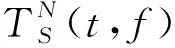

(8)

考虑到TMSSWT属于TSST类方法,应与其具有相同的反变换公式,而TMSSWT是在时间方向上进行“挤压”,并未破坏W变换的可逆性,因此可推导出逆变换公式,被表示为

(9)
2 理论模拟与分析
双线性调频信号是公认的检验时频谱的时频聚焦性优劣性能的模型,因此,本文首先利用双线性调频信号验证该方法的有效性。

图1 双线性调频信号的原始波形图Fig.1 The original waveform of the dual chirp signal

图2 不同方法的时频谱Fig.2 Time spectrum of different methods
图1是双线性调频信号的原始波形图。图2分别是由ST、WT、TMSSWT(N=1)和TMSSWT(N=6)对图1中的双线性调频信号进行计算时得到的时频表征结果。从图2(a)可以看出,基于ST的时频谱,某一时刻的能量总是分布在以某个瞬时频率为中心的一定频率范围内,能量分布较为模糊,使得变换后的频率分辨率相对较低且交叉点处能量混叠十分严重。由图2(b)可知,W变换相较于ST能量更为聚焦。由于TSSWT是对W变换时频谱的能量进行了“挤压重排”,把原本模糊化的信号能量重排挤压到实际频率处,因此使得TMSSWT(N=1)和TMSSWT(N=6)的时频谱的能量更加的集中,如图2(c)和图2(d)所示。通过图2(c)和图2(d)的对比可知,随着挤压次数的增加,TMSSWT(N=6)较TMSSWT(N=1)的频率分辨率更高,能量更加集中,时频聚焦性更好。此外,在图2(d)中红色箭头所指处,相对于WT,TMSSWT(N=6)没有明显的“阶梯”振荡。对比图2(a)和图2(d)可知,TMSSWT(N=6)相对于ST,通过能量挤压重排可以消除因基本小波视频率造成的S变换的时频谱在频率方向成周期延拓的效应,大大提高了TMSSWT(N=6)的时间分辨率。通过对比4种变换方法的时频谱可知,虽然这4种时频谱分析方法均能表征信号的时频分布特征,但是TMSSWT(N=6)随着挤压次数的增加,其时频谱分析方法具有更高的时频分辨率,有利于提高信号中信息提取的精度。
3 轴承故障振动信号分析
利用轴承数据(外圈故障)[24]作为实际例子,与其他方法对比来验证提出方法的有效性。如图3所示,这个测试台由一个2马力的马达(左),一个扭矩传感器(中)和一个功率计(右)构成。测试轴承支撑电机轴,通过点火花加工,在轴承外圈引入单点故障,使用安装在带有磁性底座外壳上的加速度计采集振动数据[25]。当前电机轴的转速为 1 797 r/min,采集数据的采样频率为12 kHz。根据相关参数可计算出外圈的故障特征频率分别为107.3 Hz,进而依据故障特征频率的倒数可得相邻两个瞬态间的间隔分别为9.32 ms[26]。

图3 测试台结构Fig.3 Test bench structure
图4展示了外圈故障振动信号的波形和它的频谱。可看出当滚珠通过外圈缺陷时波形被很沉重的噪声包围着,呈现周期性脉冲特性。由于其不固定的振幅以及噪声的影响,导致有些瞬态的振幅过小被噪声淹没,很难从噪声中区分开来,同时外圈具有较大的故障特征频率,因此难以从时域信号中准确获取相邻两个瞬态间的间隔,这些都给识别轴承故障特征频率带来了很大的挑战。图4(b)表明该信号的频率主要分布在2.5~4.0 kHz的范围内,为了更清晰地显示信号的时频特征,聚焦于不同方法在该频率范围内表征的时频信息。

图4 轴承信号案例Fig.4 Bearing signal case
观察图5所示的时频表征结果,着眼于整体,STFT表征的时频能量聚焦性最差[图5(a)];W变换和TSST次之,但它们的时频脊线附近仍然存在能量发射现象,如图[5(b)和图5(c)]局部放大图所示。尽管该信号相邻瞬态间的间隔较小,但TMSSWT仍能有效地识别出每个瞬态的时频特征;即使该瞬态的振幅过小,着眼于局部放大图,TMSSWT的时频能量高度聚焦,在时频脊线附近基本看不到能量的扩散[图5(d)]。此外计算了这4种方法的Rényi熵,依次为6.75、6.49、3.53、0.45,不论是从定性还是定量分析的角度,都说明了TMSSWT的时频能量聚焦性更强。
由于TMSSWT能更加细致地刻画这种脉冲特性的时频脊线,这将有利于准确刻画出机械信号的脉冲特性。在本文研究中采用了一种时频包络谱的方法去提取轴承故障的脉冲特性[27]。
首先计算TMSSWT表示的每个频率点的包络谱的最大值,使用TFES值最大的频率点的TMSST结果来表示轴承故障的脉冲特征,如图6(a)所示,结果显示在频率为3.43 kHz处具有更强的时频振幅,因此从此处对应的时频谱上提取出其对应的脉冲特性,如图6(b)所示。可见,该轴承故障所具有的每一个脉冲特性都能被准确地识别出来,此外,图6(b)中双向箭头标注了两个脉冲特性的时间间隔为9.34 ms,该值十分接近理论值(9.32 ms),这表明提出方法能有效地用于轴承外圈故障的诊断。

图5 不同方法的时频谱Fig.5 Time spectrum of different methods
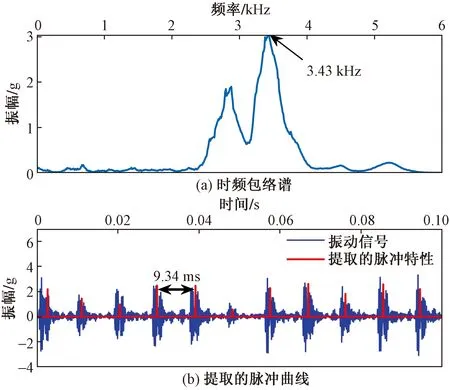
图6 外圈轴承故障分析Fig.6 Fault analysis of outer ring bearings
4 结论
提出了一种高精度诊断轴承故障的时间多重同步挤压W变换方法(TMSSWT),用于增强信号在时频域的能量聚焦性。该方法通过对W变换时频谱的能量进行了“挤压重排”,把原本模糊化的信号能量重排挤压到实际群延迟脊线处,从而得到聚焦的时频表征结果,由TMSSWT产生的高度集中的TFR可以来表征故障信息,这对于准确的轴承故障诊断非常有用。证明了本文提出的信号分析技术可以用于信号重构。在本研究中,使用双线性调频信号以及一组受噪声污染的模拟轴承缺陷信号,评估了所提出技术的有效性。分析结果证实,本文所提出的技术优于其他时频分析技术,TSSWT能提供一个更加聚焦的时频表征。此外,将该方法应用于实际资料可以较好地诊断轴承故障,表明该方法可以显著提高分辨率,在实际资料处理中具有可行性和适用性。

