高速列车受电弓气动噪声数值模拟

韩斐， 周毅*

(1.中国空气动力研究与发展中心气动噪声控制重点实验室, 绵阳 621000； 2.南京理工大学能源与动力工程学院, 南京 210094)

随着高速列车运行速度逐步增加，由此引发的气动噪声不仅造成车内的噪声污染，还会严重影响周边居民的生活[1-2]。当列车速度超过250 km/h，气动噪声成为列车噪声源中贡献最大的部分，并与运行速度的六次方成正比[3]。Nagakura[4]发现高速列车主要噪声源是受电弓、转向架区域。受电弓作为高速列车气动噪声主要噪声源之一，由于外形复杂导致周围的流场具有强烈扰动，并对周围流动产生影响[5]，故研究其流场特性及气动噪声特性，对理清受电弓噪声产生机理以及噪声传播特性，从而降低气动噪声，减少噪声污染有着极其重要的意义。

列车运行时受电弓表面边界层压力变化导致尾流区产生旋涡[6]，由于这些旋涡的产生、脱落、碰撞、消散和再附着，会使受电弓的受力发生剧烈变化，以致其周围流场产生复杂的湍流边界层流动状态，这种不同尺度的涡与涡之间相互碰撞以及受电弓不同柱体间的相互干扰，产生了不同频率的脉动压力，从而产生气动噪声。目前中外学者对受电弓流场及其气动噪声问题进行了一系列研究，主要的研究手段是基于实验分析及数值模拟。

实验分析方面，Iwamoto等[7]与Ikeda等[8]通过理论与实验相结合的方法，分别提出了降低受电弓噪声的设计方案。Noger等[9]在低噪声风洞中通过实验来测试受电弓的气动噪声源，发现受电弓背部是重要的气动噪声源区域，并且发现这一区域流场运动最为复杂。蔡国华[10]在中国航天空气动力技术研究院FD-09低速风洞进行试验，研究了高速列车受电弓的整弓气动阻力，为改进受电弓气动力和气动噪声特性提供准确而可靠的依据。高阳等[11]通过气动-声学风洞试验平台，对包含受电弓的整车模型进行气动噪声试验并分析了主要噪声源特性，研究发现受电弓以及转向架产生的噪声是模型最主要噪声源。张毅超等[12]通过对同一受电弓以开、闭口运行状态来开展噪声现场跟踪试验研究，发现闭口状态噪声能量在各个频段高于开口状态。

而数值模拟计算方面，King[13]将受电弓等效为圆柱体，通过偶极子声源来描述柱体旋涡脱落引起的气动噪声，探讨了受电弓的远场气动噪声。Takaishi等[14]通过大涡模拟与紧致Green函数的混合方法研究了受电弓偶极子噪声源。Yoshiki等[15]通过格子Boltzmann方法得到受电弓的气动噪声与试验结果吻合较好。Shi等[16]采用不可压缩流体流动分析和边界元声学分析相结合的方法，对单臂受电弓表面偶极子声源的分布及其噪声辐射进行了数值模拟，发现该型号受电弓气动噪声主要是低频与中频噪声。杜健等[17]利用计算流体力学原理和FW-H方程对受电弓远场气动噪声进行分析，发现受电弓远场气动噪声具有明显的指向性。罗乐等[18]基于大涡模拟和直接边界元法对受电弓进行数值模拟，研究表明受电弓引发的气动噪声是一种宽频噪声，噪声频谱在中高频段的幅值明显降低，但扩散区域更为广泛。Tan等[19]通过大涡模拟(large eddy simulation，LES)与FW-H方程得到受电弓远场气动噪声，发现受电弓的漩涡结构具有一定周期性，并提出了一些相应的声学优化方法。姚永芳等[20]采用延迟脱体涡模拟和声学有限元相结合的方法，并分析了不同建模方式对噪声幅值和指向性的影响。赵萌等[21]通过采用分离涡模拟方法对受电弓不同姿态运行时的非定常气动特性进行了相关研究，并探讨了受电弓在不同开口方向下运动时扰流特性的相关差异，发现闭口状态下受电弓受到干扰强烈。秦登等[22]通过DES分析了受电弓在不同运行状态下的流场特性以及气动特性，发现不同运行状态下列车受电弓气动性能有差异较大，并指出所研究型号受电弓上碳滑板引起的噪声主频特性非常明显。曾昭阳等[23]通过简化受电弓弓网系统，建立弓网耦合系统的动力学模型，并对受电弓的激励力频幅特性进行了预测，发现受电弓的激励幅值随着频率的增加逐渐减小。柳丛彦等[24]基于Lighthill声类比理论混合方法主要探讨了受电弓表面偶极子声源的分布规律及频谱特性，并通过有限元法计算远场噪声辐射特性。

如上所述，目前前人关于高速列车受电弓的研究大都集中在受电弓气动力以及气动噪声频谱特性等相关方向。而对于受电弓上引起气动噪声的具体部件贡献量的研究较为缺乏，除此之外，对于独立受电弓在不同开口方向及不同运行速度下的流场和气动噪声特性也有待于作进一步对比研究。因此，现采用大涡模拟和基于Kirchhoff积分的K-FWH (Kirchhoff-Ffowcs Williams Hawkings)方程相结合的方法，以受电弓表面为积分面对受电弓流场以及声场进行数值模拟。首先验证串列双圆柱标准算例流场以及声场特性，证明数值方法及声场求解算法的准确性。其次，使用快速傅里叶变换(fast Fourier transform,FFT)得到不同速度下声压级频谱，并对受电弓各部件上引起气动噪声的贡献量进行研究。再次，通过对受电弓周围监测点的频谱分析，得到远场指向性分布。最后，对比分析不同速度与开口方向下远场声压的幅值变化，以期为工程降噪问题提供参考数据。

1 数值方法

采用LES进行数值模拟，利用壁面自适应局部涡粘WALE (wall adapting local eddy viscosity)亚格子模型进行模拟。WALE模型可以合理地预测壁面附近的涡黏性，能正确反映壁面涡流黏度衰减与垂直壁面距离的三次方的正比关系[25]，且表达式中不包含关于边界几何尺寸的参数，较易应用于复杂情况的湍流模拟。该模型表达式为

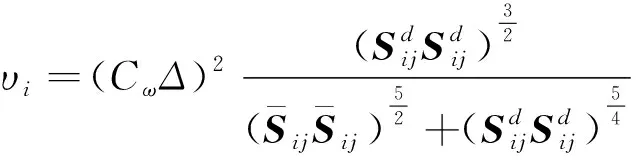
(1)

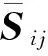
通过引入赫维塞德广义函数，按照流体运动波动方程形式，将Navier-Stokes方程重新整理成FW-H方程[26]，表达式为

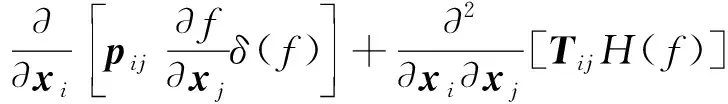
(2)

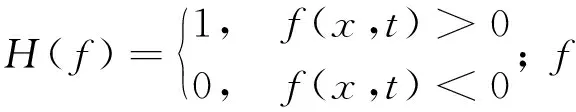
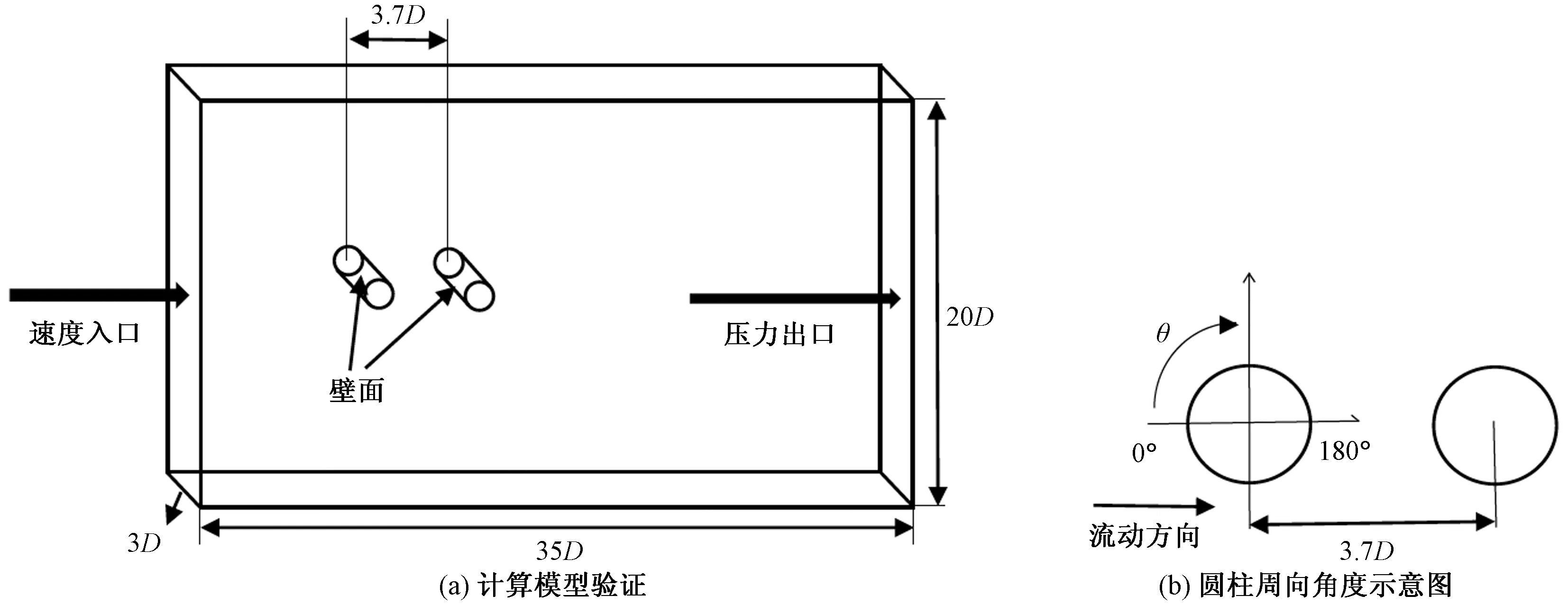
D为圆柱直径图1 计算验证模型示意图Fig.1 Schematic diagram of calculation verification model

式(2)等号右边第一项是由δ(f)函数决定的面声源，性质属于单极子声源，第二项是由δ(f)函数决定分布于物体表面的面声源，性质属于偶极子声源，第三项是由赫维塞德函数决定的分布于流体中的体声源，性质属于四极子声源[27]。依据文献[28-29]，低马赫数流动(小于0.3)可以近似看作不可压缩流动进行计算，而本文最大运行速度为350 km/h，马赫数约为0.286(小于0.3)，因此属于不可压缩范畴。受电弓弓体表面可以看作刚性壁面，其与气流之间的耦合作用非常小，体积脉动量几乎为0，故不用考虑单极子源的影响。对于亚声速流动，偶极子噪声贡献占总噪声的绝大部分，四极子与偶极子声源强度之比正比于马赫数平方[30]，由于马赫数约为0.286，故四极子声源所占比重远小于偶极子声源，可忽略不计。Zhang等[1]、杜健等[17]和柳丛彦等[24]基于理论分析，在研究受电弓气动噪声过程中忽略了单极子和四极子源，只考虑偶极子源，所得结果与前人试验结果[31-32]吻合良好。除此之外，杜健等[17]还在中国空气动力研究与发展中心的航空声学风洞中开展了受电弓噪声试验，试验结果也与数值模拟结果相吻合。故在本文研究中，只考虑偶极子声源。

采用K-FWH声压时域解公式是在FW-H方程的基础上结合Kirchhoff方法在OpenFOAM开源软件中实现的，主要的优点是不需要表面压力法向导数[33]。简化后求瞬时声压p′时域解公式为

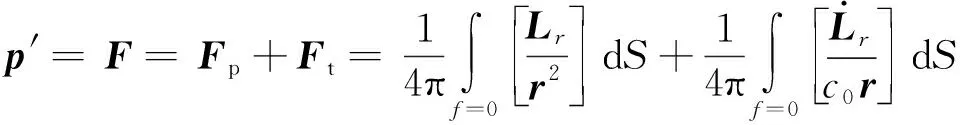
(3)

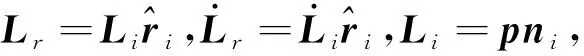
2 计算方法验证模型

2.1 计算模型设置

受电弓模型的部件在外形结构上可以与圆柱进行类比，所以本文选取串列双圆柱模型进行计算方法可行性与准确性验证。参照标准算例[34]验证过程，对串列双圆柱流场进行模拟，首先通过LES求解不可压Navier-Stokes方程得到非定常流场；然后以圆柱表面为积分面，结合K-FWH方程时域解进行积分求解，得到监测点的声压时域值，即远场噪声。计算模型如图1(a)所示，图1(b)中θ为沿圆柱顺时针方向圆周角度。串列双圆柱由两个直径相同的沿来流方向串列排列的圆柱体组合而成，坐标系原点为上游圆柱中心点。圆柱直径D为0.057 15 m，整个计算域流向长度35D，法向长度20D，展向长度3D，两个圆柱中心点之间的距离为3.7D。

在圆柱表面共设置6层边界层网格，法向增长率为1.2，对靠近圆柱部分进行加密，并保证壁面无量纲量y+< 1，网格总量约为91万。边界条件设置均匀速度入口Uin=43.4 m/s，压力出口以大气压为参考，圆柱表面设置无滑移壁面边界条件，其余边界面为周期性边界条件。基于圆柱直径和来流速度的雷诺数为Rein=UinD/v=1.66×105，其中Uin为入口速度，v为动力黏度。时间项采取二阶隐式离散格式，使用高斯积分计算梯度，中心差分进行插值，时间步长Δt=4×10-6/s。本文计算所得流场与声场数据皆是在流场达到相对稳定之后开始统计，采样时间170 000时间步，对应总的计算时间为0.68 s，约123个旋涡脱落周期。

2.2 数值模拟及声场计算验证

图2所示为X-Y平面无量纲化瞬时流向速度云图及流线图。圆柱两侧红色区为局部高速区域，蓝色区域为局部低速区域。通过流线图也可以显著看到流场中的回流区。图2中可以清晰看到圆柱背风面的附着涡，上游圆柱尾部一侧的涡向中心线移动并向下游转移，流场下游也会出现向中心线移动现象。此外在圆柱下游出现类似卡门涡街的旋涡脱落现象。

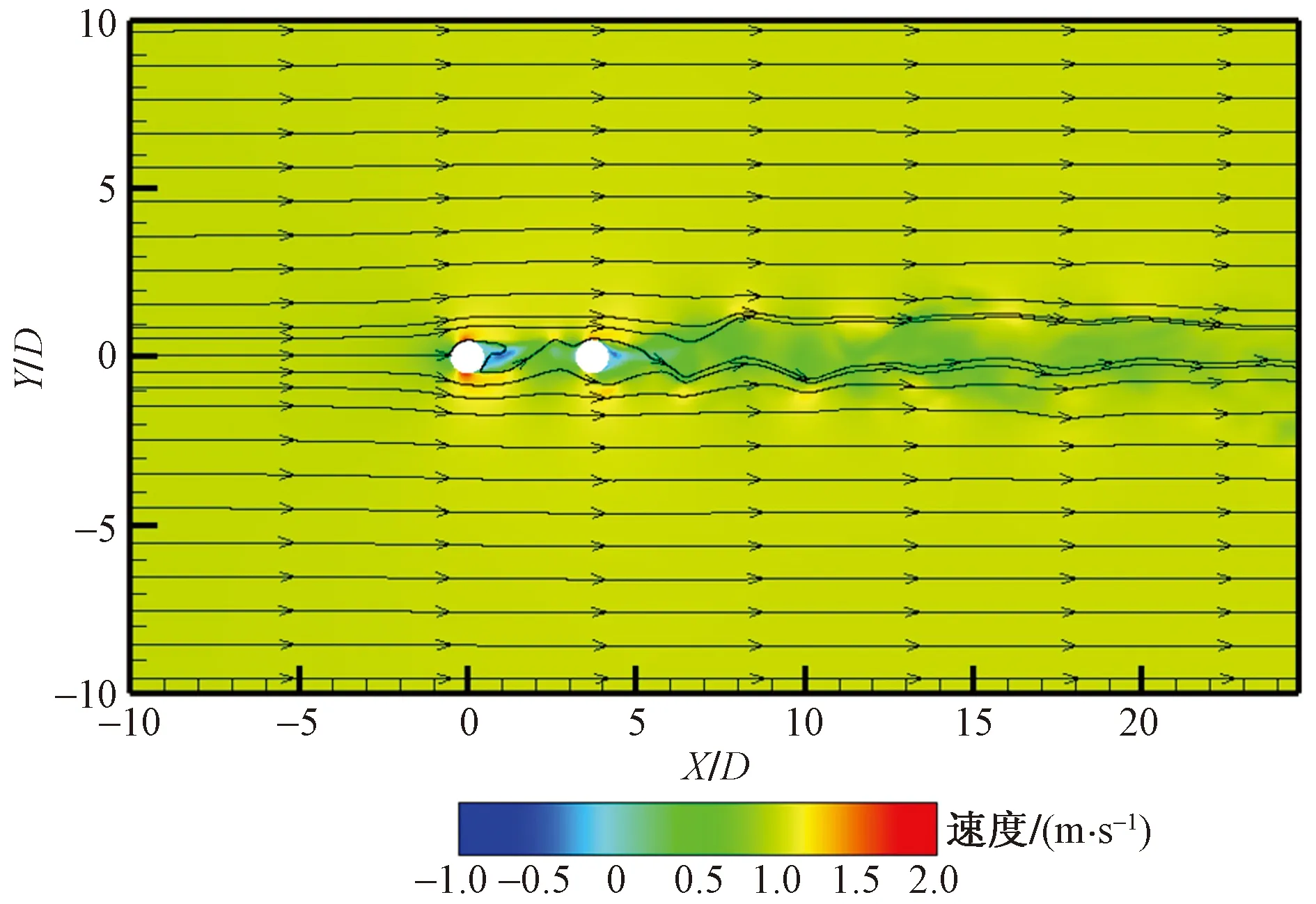
图2 X-Y平面无量纲瞬时流向速度云图及流线图Fig.2 Instantaneous flow velocity diagram on X-Y plane and streamline diagram

图3所示为上下游圆柱时均压力系数沿圆柱表面的分布，结果与Lockard[34]的实验数据及余雷等[35]的数值模拟结果吻合良好。圆柱表面时均压力系数沿周向对称分布，上游圆柱正对来流方向处最大压力系数值为1。随着流速逐步提升，压力系数顺着圆周方向逐步减小，在75°及285°达到最大负压，之后沿圆周方向压力系数有所提高，在圆柱背面形成负压回流区，压力分布比较稳定。由于上游圆柱的涡作用于下游圆柱，形成更为复杂的涡结构，下游圆柱正对来流处压力系数小于上游圆柱的同样位置。上下游圆柱均在圆柱背面较稳定区形成均匀的压力分布。

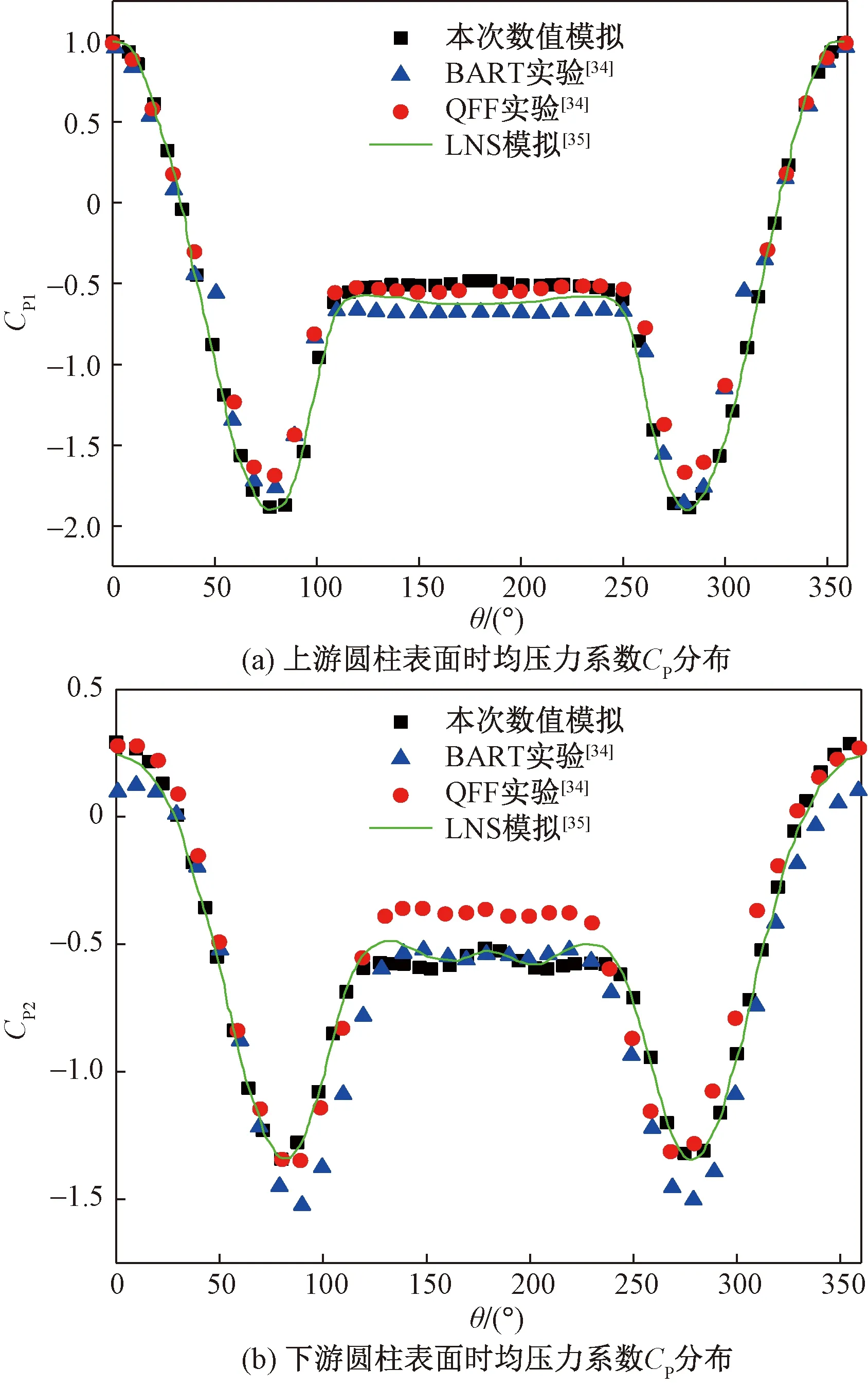
图3 上下游圆柱表面时均压力系数Cp分布Fig.3 Distributions of the time-averaged pressure coefficient Cp on the surface of the upstream cylinder and the downstream cylinder

通过FFT将监测点处的声压信息从时域转化为频域，得到取样带宽为10 Hz的频谱。如图4所示为监测点(9.11D, 32.49D, 1.50D)的噪声功率谱密度，并与Lockard[34]的实验进行对比。图4中功率谱密度主级峰频率f=180.4 Hz，次级峰频率f=545.3 Hz。明显地看到功率谱密度(PSD)在主、次级峰频率和峰值方面均与实验吻合良好，证明了本文计算方法的可行性以及准确性。

3 受电弓流场特性以及气动噪声特性

3.1 受电弓模型

高速列车受电弓作用于车顶，由上下臂、底架、碳滑板和弓角等部件构成。为了网格划分的合理性以及简易性，在不影响主要气动特性条件下，对实际受电弓模型进行简化，忽略了弹簧、推杆和平衡杆等部件，简化后的受电弓模型如图5所示。

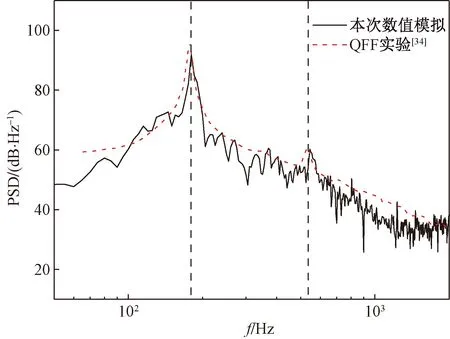
图4 监测点处的声压级功率谱密度Fig.4 Power spectral density of the sound pressure level at the monitoring points

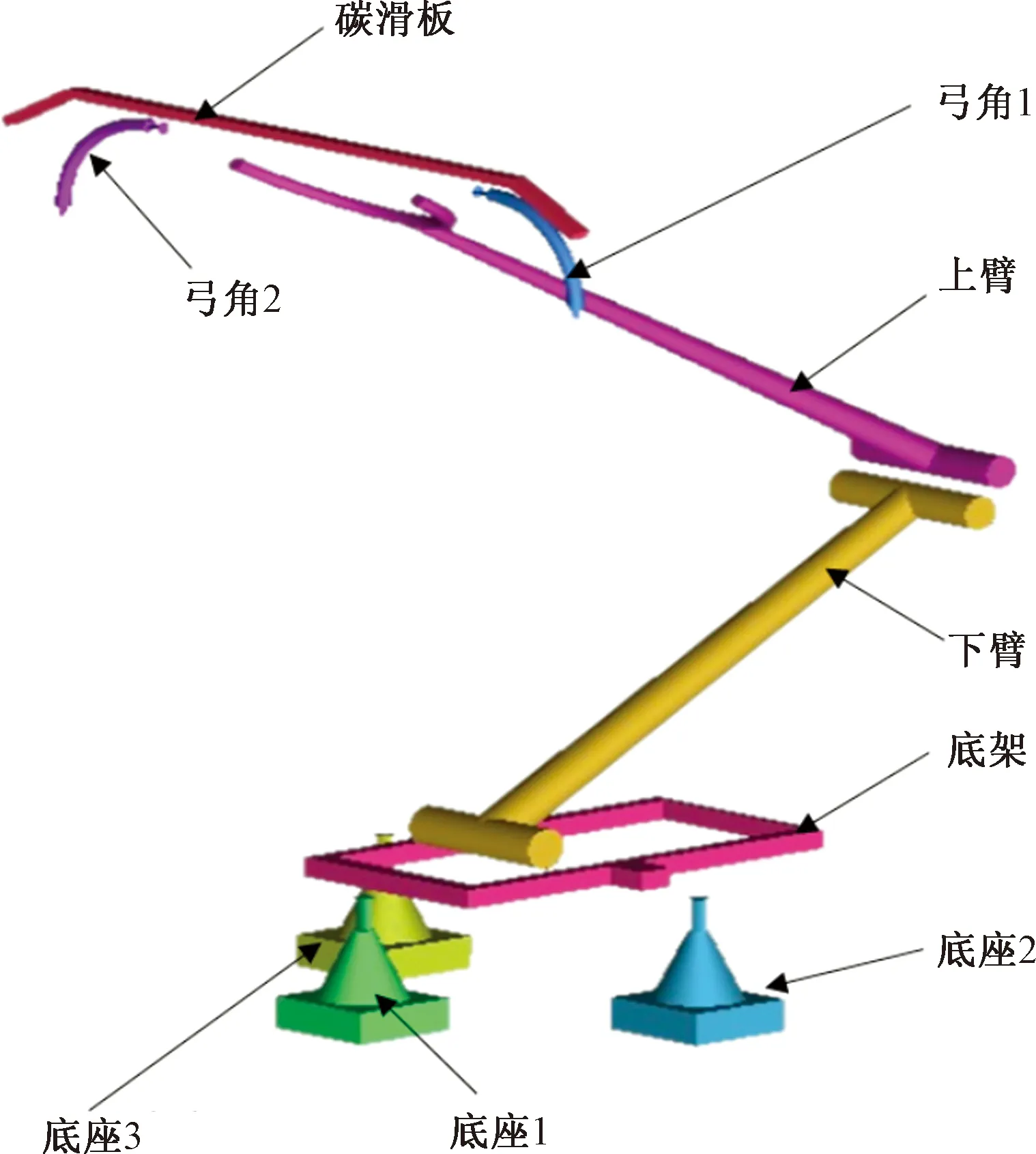
图5 受电弓结构示意图Fig.5 Schematic diagram of pantograph structure

3.2 计算域模型设置及网格划分

受电弓外流场计算域模型如图6所示，具体参数为：流向(X方向)21.3 m；法向(Y方向)8.875 m；展向(Z方向)10.65 m。开闭口状态与高速列车行驶方向有关，开口状态是指受电弓上下臂的夹角与来流方向反向这一状态，闭口状态则正好与开口方向相反，上下臂的夹角与来流方向同向。受电弓纵向对称面与流域纵向对称面重合，开闭口状态下坐标系原点均为底座1前沿中点位置。

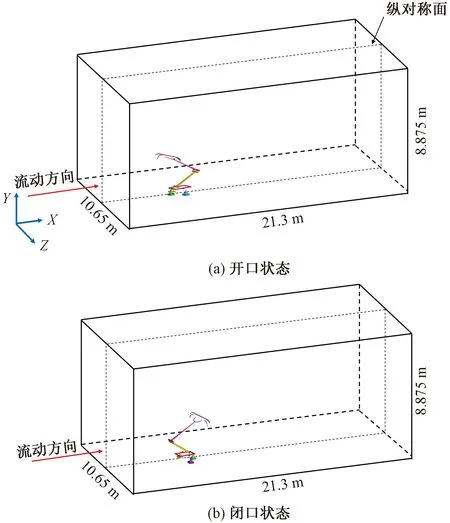
图6 受电弓计算域Fig.6 Pantograph calculation domain

受电弓位于计算域底部边界上，受电弓前部距入口处7.1 m，Z方向边界距受电弓中轴线5.325 m。受电弓在流向(X方向)最大长度2.46 m，展向(Z方向)最大长度1.9 m。由于受电弓外形结构复杂，采用非结构网格来划分外流域。考虑到模拟结果准确性，对湍流剧烈区域进行网格加密处理。依据杜健等研究结论[17]，受电弓表面网格尺寸不超过10 mm，可保证受电弓噪声计算准确性，综合考虑计算机性能后，设置6层边界层网格，增长率为1.2。整个计算域网格划分如图7所示，图7给出受电弓开口状态下计算区域网格示意图，开闭口状态下总网格数分别为480万和550万。边界条件具体设置如表1所示，设置思路为受电弓静止不动，来流以列车时速沿着受电弓前进方向的相反方向来模拟受电弓在实际生活中的运行过程，由于目前中国大部分高速列车都是以350 km/h及以下速度运行，故本文最大速度设置为350 km/h。本文计算时间步长Δt=2×10-5s，声场数据采样频率间隔为2.5 Hz，库朗数约为1.75，采样时间25 000时间步，对应总的计算时间为0.5 s，以保证流体流经整个计算域。

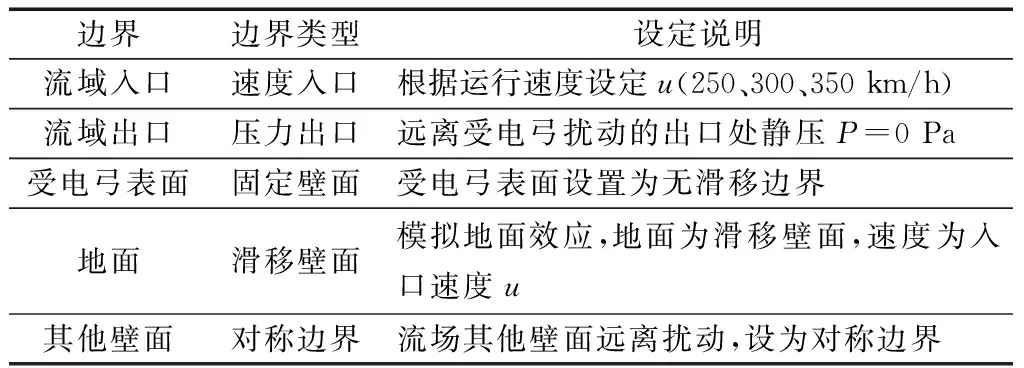
表1 边界条件设置Table 1 Boundary condition setting

图7 受电弓流域网格划分示意图Fig.7 Schematic diagram of grid divisionin pantograph basin

3.3 噪声监测点设置

为了研究受电弓的远场气动噪声特性，根据ISO3095—2013噪声监测标准[36]在受电弓周围设置噪声监测点，监测点位于距离原点7.5 m或者25 m处位置，高度为1.2 m或者3.5 m。本文X-Z平面选择监测点以7.5 m为半径，1.2 m高度每隔10°取一个监测点，而X-Y，Y-Z上半平面选择的噪声监测点是每隔10°以7.5 m为半径所取，如图8所示。

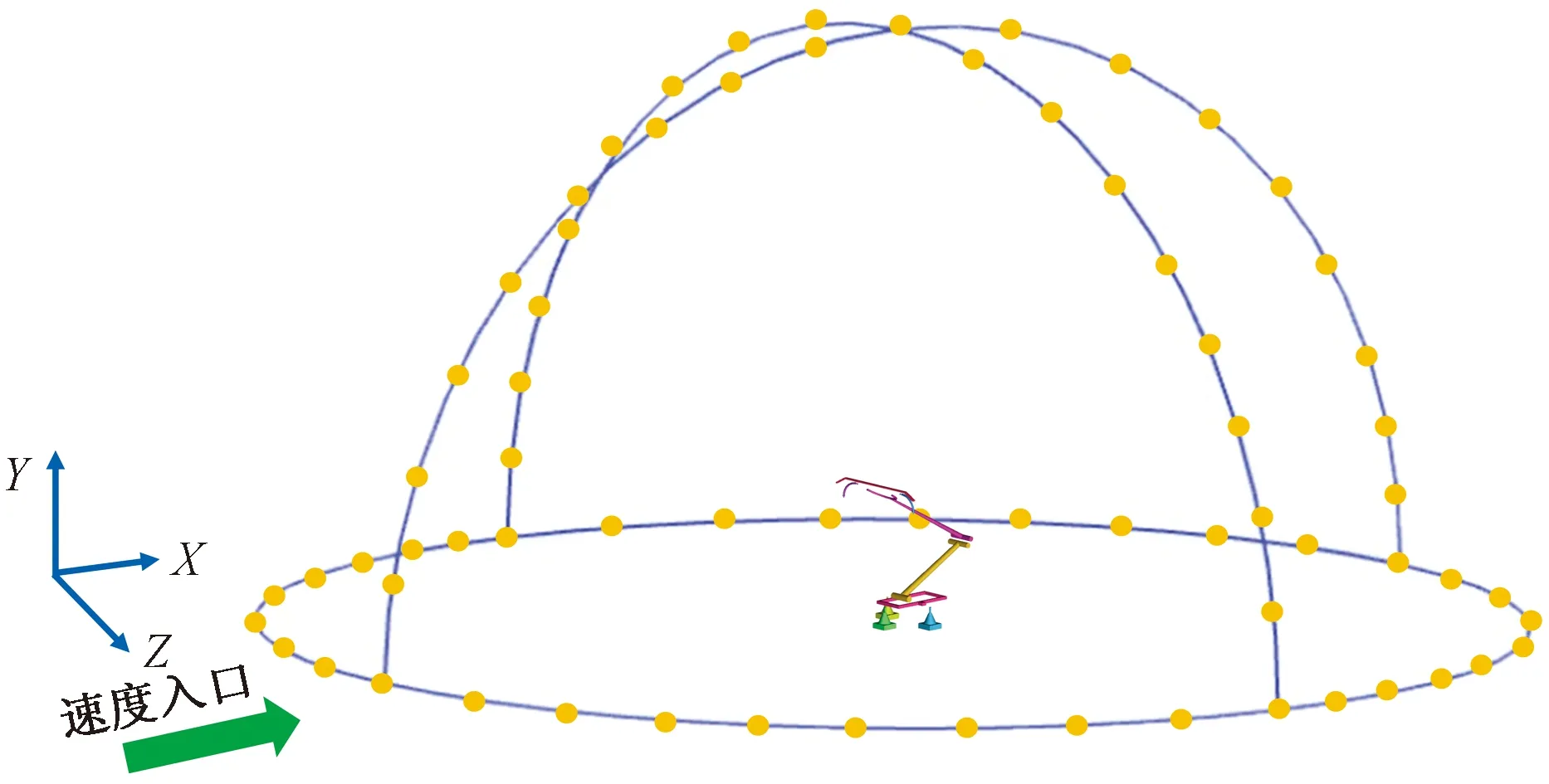
图8 受电弓远场噪声监测点示意图Fig.8 Schematic diagram of pantograph far-field noise monitoring points

沿展向及法向噪声监测点设置如图9所示。沿原点远离弓体，垂直向外区域方向，分别间隔3.75、3.75、7.5 m取不同监测面，而在受电弓法向方向，监测点的纵坐标分别是0.4、1.4、2.8、5、10、15、25 m。

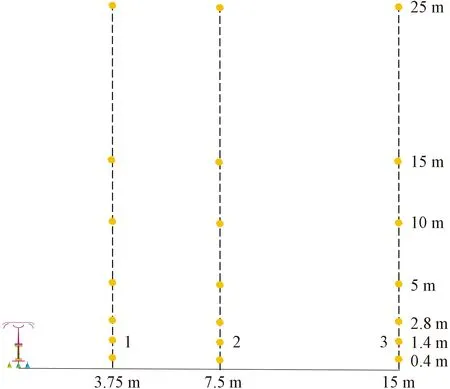
图9 沿着展向以及法向噪声监测点布置图Fig.9 Layout of noise monitoring points along the span and normal directions

沿流向监测点如图10所示，监测点展向距受电弓中心线7.5 m，水平面高度3.5 m，沿流向每间隔2.5 m取一个监测点。

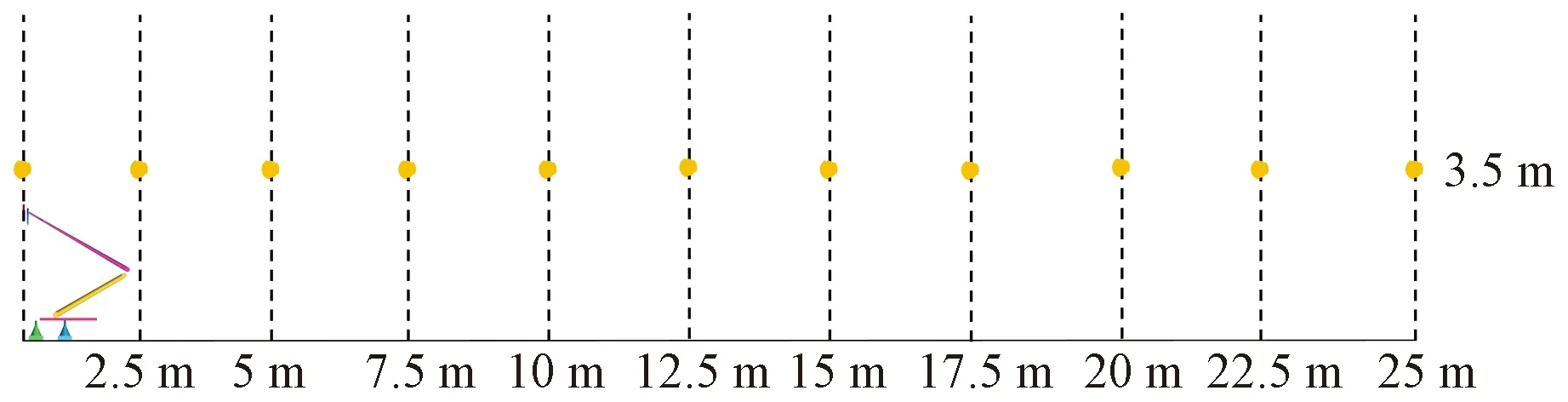
图10 沿流向噪声监测点布置图Fig.10 Layout of noise monitoring points along the flow direction

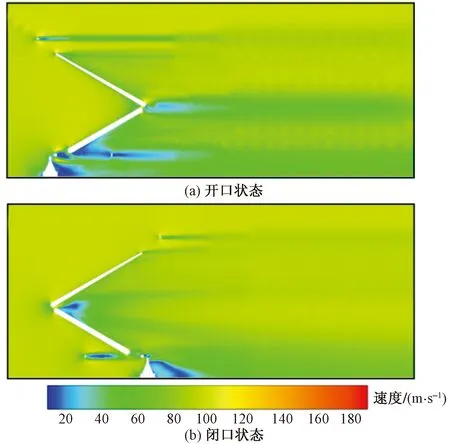
图11 受电弓中心截面Z=0 m速度分布Fig.11 Velocity distribution of pantograph central section Z=0 m

3.4 流场特性

图11所示是受电弓在350 km/h速度下垂直中心界面Z=0 m处0.7 s的时均速度云图，其中图11(a)和图11(b)分别表示开口和闭口状态。图11中低速区域大都分布在受电弓背风面。而且由于流体流动的黏性和压力，受电弓表面边界层发生流动分离而产生旋涡脱落现象。来流作用于上下臂杆迎风面时，上下臂引导气流在臂杆连接处汇集并向下游发展，所以在上下臂连接处速度较大。而低速区域则主要集中在底架以及3个底座的背风面。

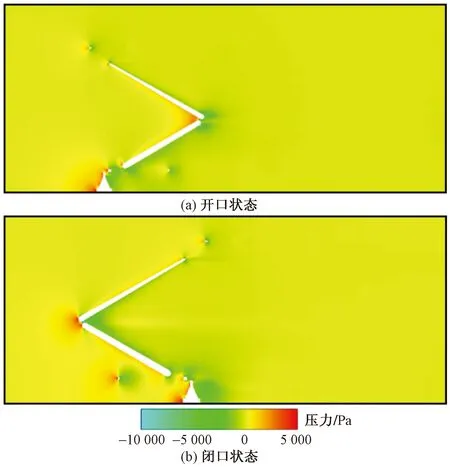
图12 受电弓中心截面Z =0 m时均压力分布Fig.12 Time-averaged pressure distribution of pantograph central section Z=0 m

图12所示是受电弓在350 km/h速度下中心截面处Z=0 m时的均压力云图。由图12可以看到受电弓碳滑板来流面、上下臂杆连接处和底架底座来流面均出现了明显的高压区。当来流绕过受电弓后，背面形成的负压区主要集中在碳滑板、下臂和底座等位置，这种前后压力差正是受电弓气动阻力的主要来源。由于上下臂杆受力不同，对来流导流特性不同，导致下臂负压区面积大于上臂。闭口状态运行时，受电弓底座背风面的低压区面积大于开口状态，由于不同开口状态下圧力分布特性不同将导致噪声声压级产生差异。

受电弓表面压力的分布情况与脉动压力相关，受电弓在350 km/h速度下表面压力分布云图如图13所示。从图13中可以看到，闭口状态与开口状态下的表面压力分布类似，迎着来流方向的受电弓表面大多都位于局部高压区，主要包括碳滑板、下臂、上下臂交界处和底座等部分，因此上述区域也是产生气动噪声的主要区域。但不同开口状态下，来流撞击受电弓表面位置不同。闭口状态迎风面最大压力6 778 Pa，而开口状态下迎风面最大压力4 709 Pa，两种状态下压力差为2 069 Pa。可见闭口状态下旋涡脱落更强，因此可以预测闭口状态受电弓引发的噪声声压级更大。

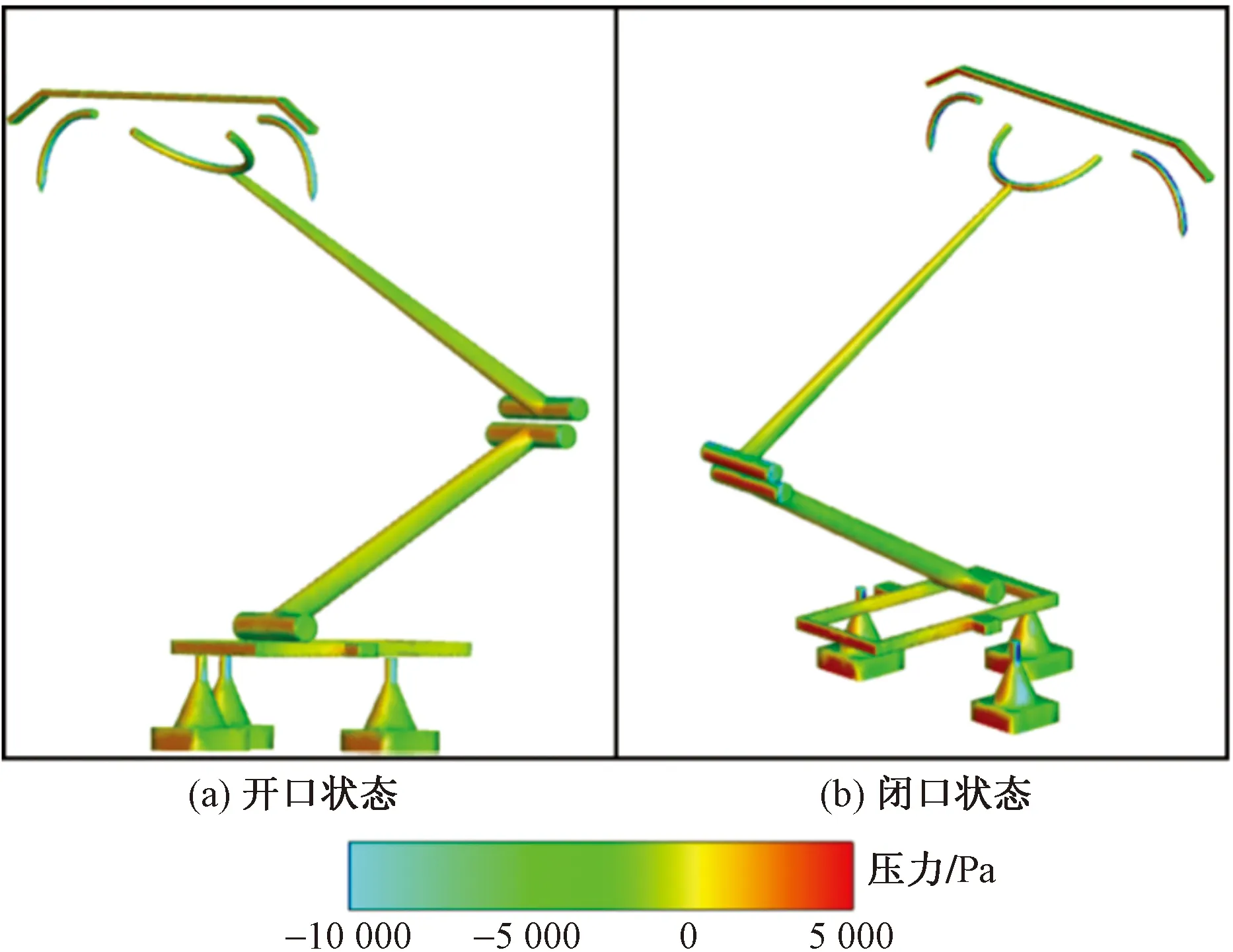
图13 受电弓表面压力云图Fig.13 Pressure distribution of pantograph surface

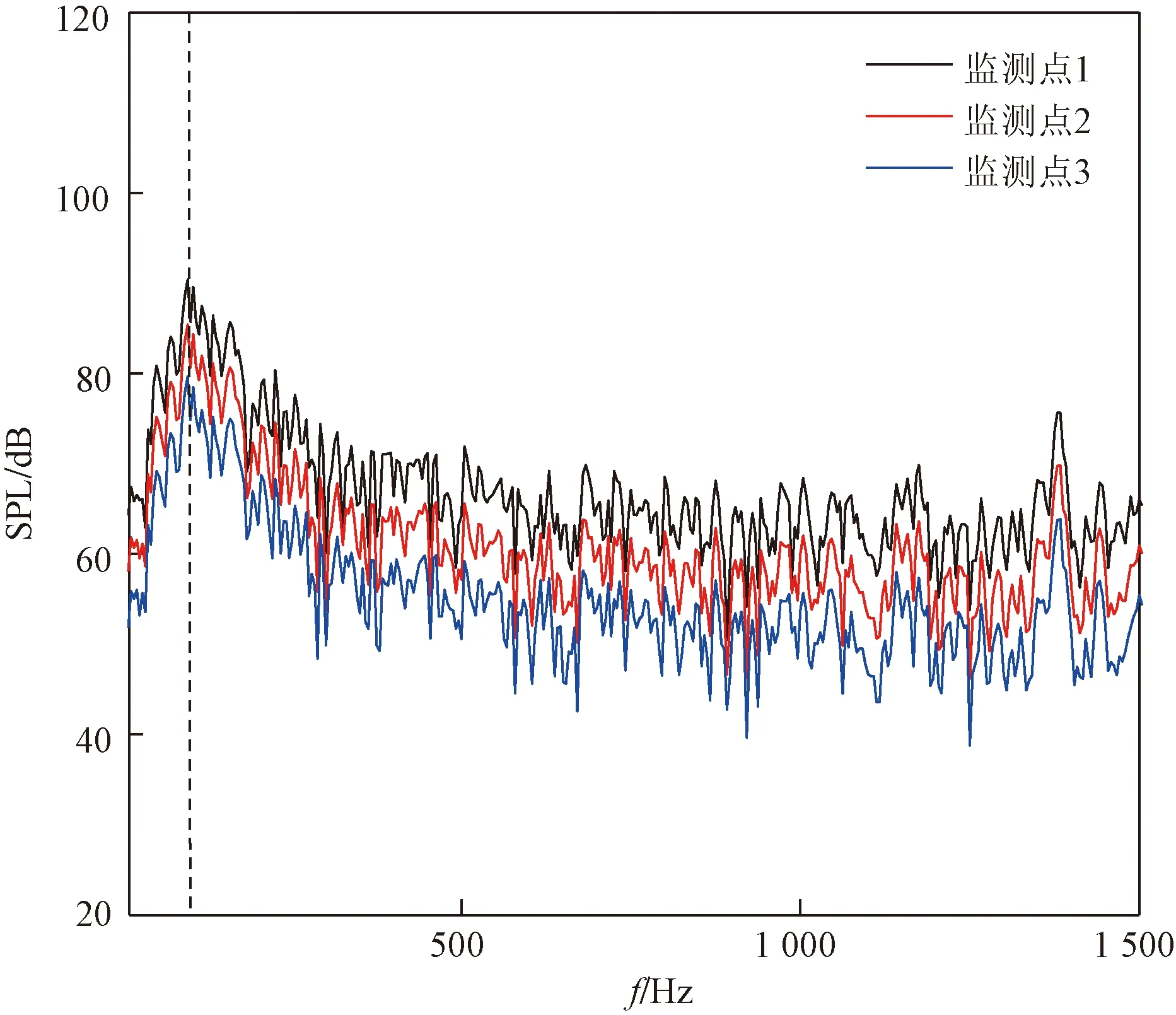
图14 远场监测点声压级频谱Fig.14 Sound pressure level spectrum of far-field monitoring point

3.5 声场特性

3.5.1 受电弓远场监测点噪声频谱

将受电弓在开口状态下以350 km/h速度运行时3个监测点瞬时声压数据经过FFT变换，得到声压级频谱如图14所示。图14中1～3噪声监测点依次表示沿受电弓的中心点为参考，流向方向0.15 m，法向方向1.4 m，展向方向间隔3.75、3.75、7.5 m取3个监测点，具体如图9所示。

受电弓模型部件在外形结构上可以与圆柱进行类比，而圆柱杆产生的气动噪声具有明显的单频特性，所以受电弓的噪声频谱也应该具有单频特性。从图14中可以看到，噪声具有明确的主级峰，频率为120 Hz。而不同监测点的噪声频谱呈现高度相似性，随着频率f的升高，幅值升高到达峰值后持续减小，当频率f> 500 Hz时趋于平缓，在一定的水平面上下波动。不同的监测点由于距受电弓位置不同，同频率下声压级幅值也不同，监测点距受电弓越近，声压级越高。

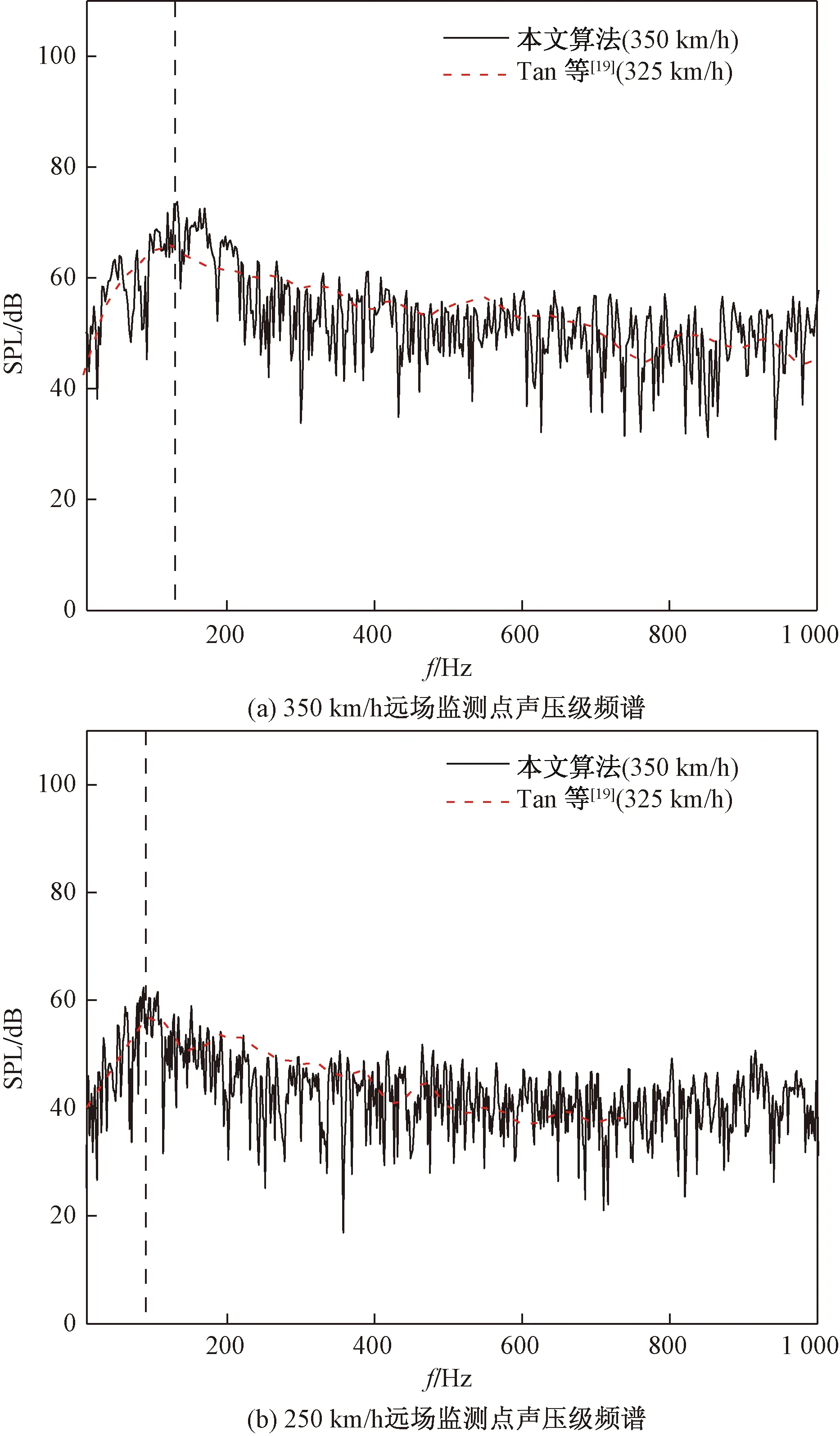
图15 0.15、25、3.75 m远场监测点声压级频谱Fig.15 Sound pressure level spectrum of far-field monitoring pointat 0.15，25，3.75 m

将受电弓开口状态下在(0.15、25、3.75 m)监测点瞬时声压数据经过FFT变换，得到不同速度下声压级频谱，并与Tan等[19]在类似监测点下的结果进行对比，同时采用相同型号单臂受电弓，但分别在325、225 km/h速度下运行。对照如图15所示。可以发现不同速度下噪声频谱峰值频率、声压级大小和曲线趋势与Tan等[19]的研究结论吻合良好，再次验证了本文算法的正确性以及网格准确性。

3.5.2 受电弓部件气动噪声贡献分析

以开口状态下列车速度350 km/h为例，研究受电弓的各个部件所引发的噪声在总噪声中贡献量。如表2所示计算得到0.15、1.4、7.5 m监测点处受电弓各部件噪声声压级，通过功率谱密度主频峰值求得声压级大小，序号与图5各部件序号相同。由表2可知，下臂产生的噪声是整个受电弓气动噪声的第一大贡献源，3个底座是第二大贡献源，而上臂所产生的噪声声压级仅次于前两个贡献源，为第三大贡献源。因为受电弓下臂及底座后方有较为明显的旋涡脱落，使得受电弓表面产生脉动压力，进而产生较为强烈的噪声。据此发现该型号受电弓远场气动噪声主要来自受电弓下部，如果在实际生活中，能够有效控制下部区域所产生的噪声，就可以有效降低受电弓引起的总气动噪声。

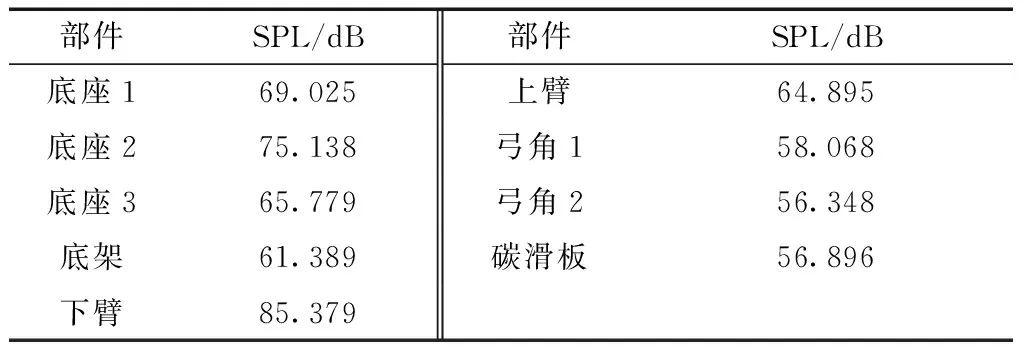
表2 受电弓各部件气动噪声声压级Table 2 Sound pressure level of aerodynamic noise for pantograph components

3.5.3 气动噪声指向性分布

图16所示是不同速度下受电弓诱发噪声在不同平面指向性分布，其中左栏是开口状态，右栏是闭口状态。监测点设置参考3.3节，开口与闭口状态噪声指向性分布相类似。图16(b)中X-Y平面上，受电弓气动噪声具有方向性，在开口状态时，50°～80°声压级幅值最大，0°与180°最小，说明受电弓产生气动噪声具有偶极子特性，噪声主要向尾流斜上方传播。而在图16(c)中，Y-Z平面上声压级基本对称分布，但在90°左右声压级最小。不同速度下声压级指向性类似，声压级随着速度增大而变大。

3.5.4 气动噪声衰减特性

如图17～图19所示是受电弓周围不同监测点声压级对比，其中左栏和右栏分别表示开口和闭口状态运行。监测点说明如下：图17是按图10设置监测点，图17(a)共计11个监测点，图17(b)由于第一个噪声监测点位于 -2.5 m，所以共计12个监测点；图18表示在x=0.15 m，z=7.5 m处，沿法向按图9所示设置监测点；图19表示在x=0.15 m，y=1.4 m处，沿展向按图9设置监测点。从图17(a)和图17(b)可以看出，沿流向噪声声压级逐渐减小，开口状态与闭口状态类似，5 m之后声压级幅值减小明显。而5 m之内的监测点，声压级幅值总体上有减小的趋势，但趋势较平缓，因为这几个监测点距受电弓原点位置相接近。不同速度下监测点声压级呈现高度相似性，只是同位置下幅值不同，说明受电弓的速度越大，声压级越高。图18(a)和图18(b)中，声压级总体呈现逐渐减小的趋势。但在图18(a)中速度为300 km/h与250 km/h下，个别点会出现反转。反转出现的原因是因为相比于监测点距受电弓的距离，监测点之间距离过小，此外受电弓弓体对声波的反射和绕射也有一定影响。图19(a)和图19(b)中沿展向噪声声压级总体上逐渐减小，直线斜率也逐渐减小。可见同一监测面上距离受电弓越远，噪声声压级衰减幅度越小。此外还可以发现开口和闭口状态下声压级衰减趋势类似，但结合图19(a)和图19(b)对比发现，相同监测点下闭口状态受电弓引发的气动噪声声压级更大，该结论与之前通过图13观测到闭口状态下迎风面最大压力比开口状态下迎风面最大压力大的结论相一致。

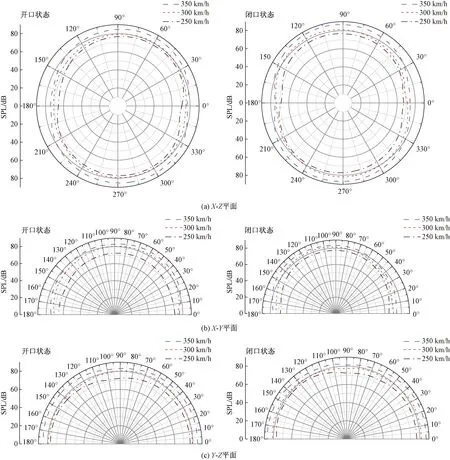
图16 受电弓诱发噪声在不同平面指向性分布Fig.16 Directivity distribution of pantograph induced noise in different planes

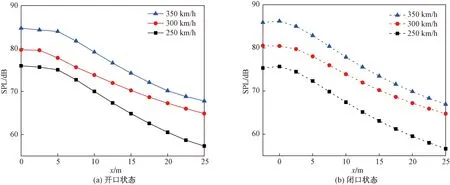
图17 受电弓沿流向监测点声压级对比Fig.17 Comparison of sound pressure levels at monitoring points along the flow direction of pantograph

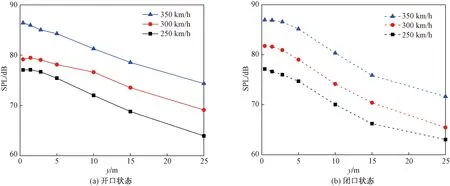
图18 受电弓沿法向监测点声压级对比Fig.18 Comparison of sound pressure levels at monitoring points along the normal direction of pantograph

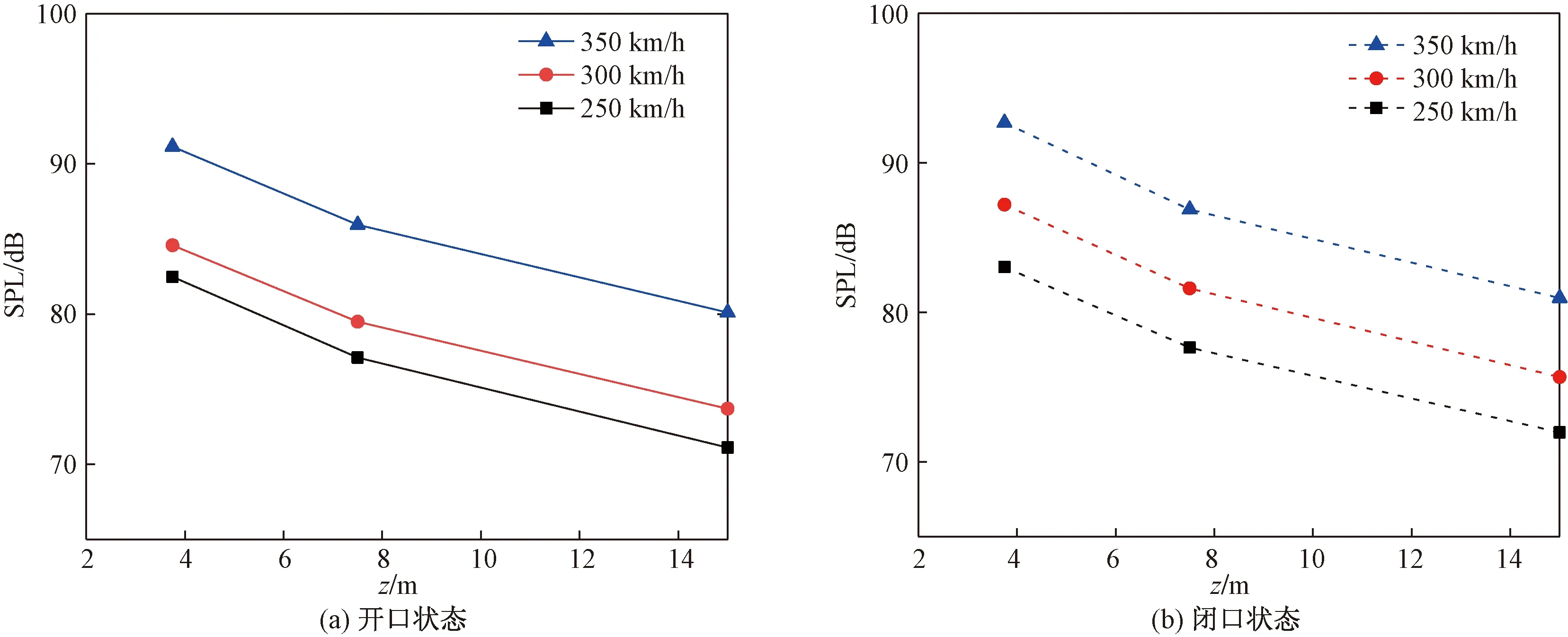
图19 受电弓沿展向监测点声压级对比Fig.19 Comparison of sound pressure levels at monitoring points along the spanwise direction of pantograph

4 结论

采用LES和K-FWH方程相结合的方法，并对数值方法的准确性进行了验证，对不同运行速度及受电弓不同开口状态下的流场以及声场进行数值模拟，对受电弓流场特性及气动噪声特性进行了研究，得出如下结论。

(1)来流在碳滑板、上下臂连接处和底架等部位会显著地发生旋涡脱落现象，导致边界层发生流动分离，进而产生气动噪声。不同开口方向下，碳滑板、下臂和底座前后面压力差是受电弓气动阻力的主要来源，也是产生气动噪声的主要区域。该型号受电弓远场气动噪声主要来自受电弓下部，对受电弓下部区域做降噪处理是很有必要的。

(2)不同监测点的噪声声压级呈现高度相似性，且随着频率f先增大到峰值后逐渐减小，之后逐渐趋于平缓，在一定的水平面上下波动。受电弓引发的气动噪声主要是低频和中频噪声并且噪声频谱具有明显的主频。

(3)远场噪声指向性方面，开口与闭口状态指向性分布类似，受电弓产生气动噪声具有偶极子特性。不同来流速度下指向性相似，速度越大，噪声声压级幅值越大。

(4)沿流向、法向和展向方向噪声声压级总体逐渐减小，距受电弓越远，声压级衰减幅度越小。闭口与开口状态下声压级衰减趋势几乎一致，但是闭口状态下受电弓引发的噪声声压级更大。