大宽跨比T梁桥的改进空间梁格算法

王邵锐， 李英斌

(重庆交通大学土木工程学院， 重庆 400074)

随着中国经济的高速发展，桥梁在两岸经济文化交流中扮演着极其重要的角色，T梁桥因构造简单，施工简单，装配能力强等优点，在桥梁建造施工中被广泛采用。在桥梁建造完成后需要定期对桥梁进行检测来确保桥梁有一个安全的通车环境。在桥梁静载试验中，需对主梁汽车荷载产生的活载内力效应进行计算，因此需计算梁的荷载横向分布系数。目前针对宽跨比较大，多横隔梁以及主梁较为密集的T梁桥，多采用“G-M法”来对荷载横向分布系数进行计算，完成活载内力效应的计算。但是“G-M法”的计算过程极为繁琐冗杂，且以往采用有限元对宽跨比较大的T梁桥进行梁格法建模，其横隔梁的模拟不够合理，不能真实的反应荷载的横向传递。为此需要寻求一种简单快捷、高效精确的方法完成主梁内力效应的计算，且计算结果与比拟正交异性板法相比需满足精度要求。

张玥等[1]提出重点分析桥面铺装、普通钢筋和预应力筋以及防撞护栏对连续T形梁桥结构整体的影响，给出了梁格模型的修正方法和建议，解决如何改进梁格法提高计算精度以及如何克服比拟正交异性板法计算繁琐的问题；苏文明等[2]采用有限元软件Midas Civil建立简支T梁桥模型，将汽车荷载作用于横向分布影响线最不利位置计算主梁横向分布系数，与传统方法计算结果分析，结果吻合较好。彭旺虎等[3]提出了一种基于模型修正理论的桥梁荷载横向分布计算方法来计算装配式T梁桥发生损伤情况下的荷载横向分布状况，通过建立考虑主梁和铰缝损伤的简化模型，定义相关参数，构造和优化目标函数，得到桥梁损伤状况下的刚度折减系数。根据修正后的刚度参数，计算出考虑主梁和铰缝损伤的荷载横向分布系数。邬晓光等[4]为了提高拼宽T梁桥内力计算精度，通过考虑旧桥湿接缝损伤和主梁刚度损伤，并根据荷载试验与外观调查确定竖向剪力折减系数和主梁刚度分配系数，在传统刚接梁法理论的基础上推导出合理的计算方法。张云虎等[5]针对简支T梁桥的跨径长度及纵梁数量，对集中荷载作用下的荷载横向分布状况进行梁格法建模分析，结果表明桥梁跨径对荷载横向分布系数影响甚微，随着纵梁数量的增加荷载的横向分布趋于均匀。陈记豪等[6]根据刚接梁法基本假定，应用力法原理推导了刚接梁法一般力法方程，可用于由截面特性和间距不同的T梁组成的非规整刚接T梁桥荷载横向分布计算。实例计算表明该方法的计算精度满足工程要求，同时对一座非规整加宽T梁桥进行了计算分析，计算结果与空间实体有限元结果吻合较好。

以上各研究都认识到了比拟正交异性板法计算的弊端以及传统梁格模型计算精度不高的问题，研究结果也都提出了合理的解决方法，但也存在一定的不足。在梁格法的改进方面，对于密排主梁上多横隔梁的梁式结构，其虚拟横梁虽然可以增强主梁的横向联系作用，但是缺乏对横隔梁作用的考虑。采用拟合曲线的计算公式对横向分布系数进行计算，虽然没有太多繁琐的计算步骤，提高了计算效率，但是拟合函数过于复杂，且不同主梁片数的拟合参数有所不同，需逐个代入计算。

针对以往研究出现的问题进行改善，现采用基于受压翼板有效宽度的大宽跨比T梁桥改进空间梁格算法计算主梁结构内力，避免了比拟正交异性板法中复杂的插值运算和粗略的查表过程。空间梁格法需克服的主要难题是如何更真实地模拟主梁间的横向联系，本文的解决方法是根据受压翼板有效宽度的原理，将梁格模型的中横隔梁受弯时的每侧翼板宽度换算成有效翼板宽度值，梁端边横隔梁截面参数不变，实现对实桥横向联系更真实的模拟。最后通过施加不同工况的移动荷载计算汽车荷载下主梁结构内力，将其与比拟正交异性板法计算结果对比分析，检验改进空间梁格法的计算准确性。

1 计算方法及原理

1.1 改进空间梁格法的基本原理

横隔梁往往伴随着主梁翼板共同起到荷载传递作用，在空间梁格建模中若仅按照实际的横隔梁截面参数建立，就削弱了主梁之间的横向联系作用，从而不能更真实地模拟梁的受力情况。根据受压翼板有效宽度原理，对于大宽跨比的T梁桥，由于横隔梁肋的间距较大，受弯时沿桥横向翼板内的应力分布受剪切应变的影响，使法向应力σx减小，导致法向应力σx不仅沿跨度方向变化，而且沿翼缘板方向也在变化，使得翼缘内的压应力沿宽度方向分布很不均匀。由于剪切变形起减小法向应力σx的作用，属于剪力滞后效应，所以在平面弯曲σx的求解中不予考虑。故本文根据受压翼板有效宽度原理[7]，把横隔板翼板的实际应力图形换算成以最大应力σmax为基准的矩形图形的长度，如图1所示，所以有

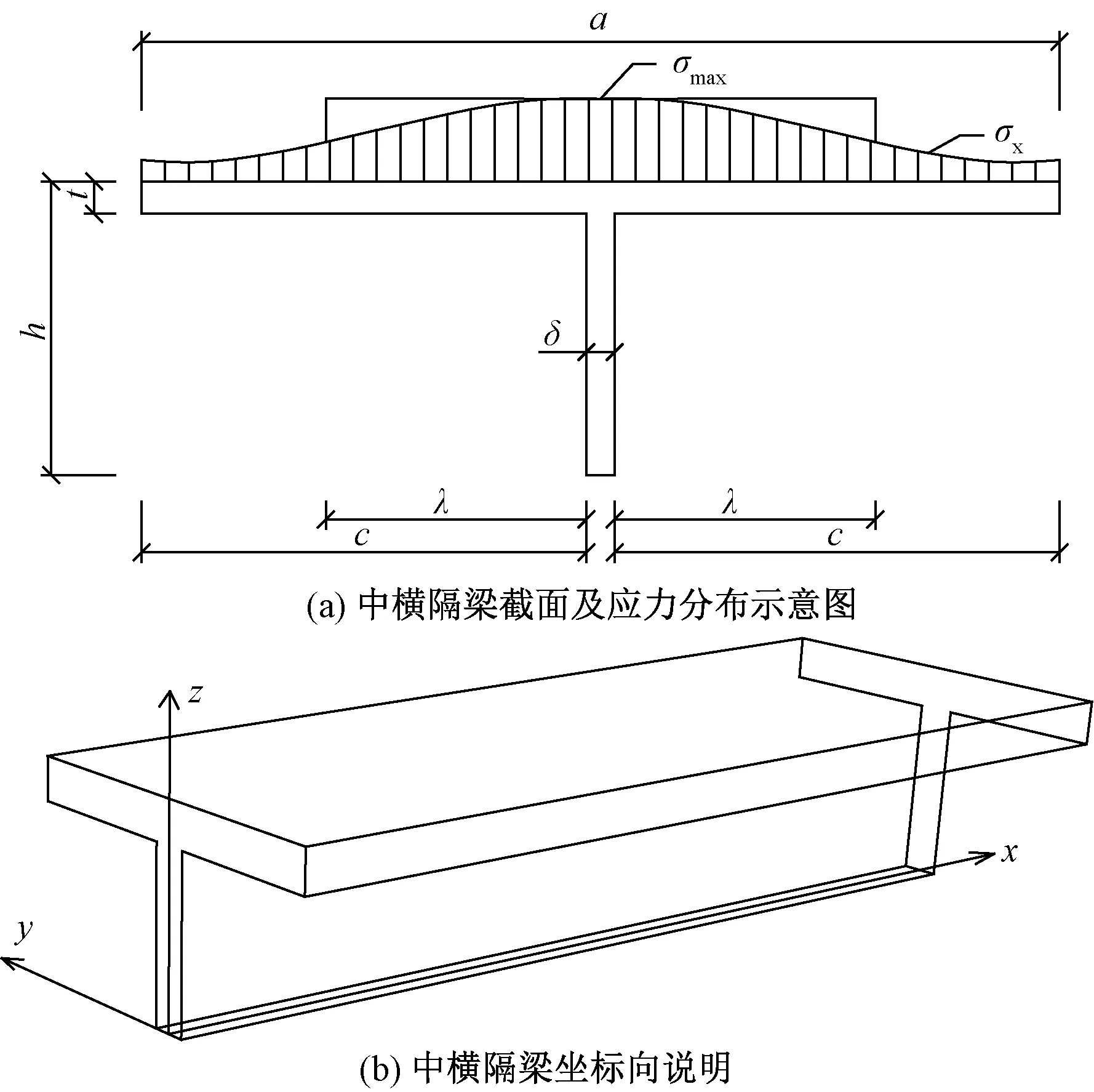
h为横隔梁高度；a为横隔梁总宽度；δ为横隔梁腹板宽度图1 中横隔梁结构示意图Fig.1 Schematic diagram of middle transverse beam structure

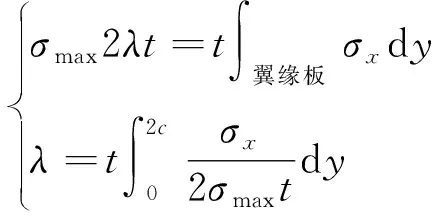
(1)

式(1)中：c为翼板宽度；λ为受压翼板有效宽度；t为翼板厚度；σx为翼板宽度方向及y方向的法向应力值。

对于多根主梁的有效分布宽度，根据文献[7]可知，σx根据弹性力学平面问题力的平衡条件所建立的3个普通偏微分方程，在满足必要条件后结合艾雷函数，σx可表达为

(2)

结合简支边界条件下弯矩的n项傅里叶级数表达方式，艾雷函数φ可用变量分离的方法，即

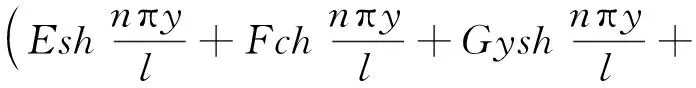
(3)

式(3)中：φn为满足偏微分方程必要条件下的艾雷函数；n=1,2,…；E、F、G、H为艾雷函数中的4个待定常数；l为计算跨径；x为沿跨长方向；y为翼缘板宽度方向。

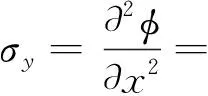
(4)

式(4)中：ν为泊松比。

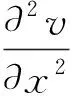
(5)

根据以上4个边界条件，可解φn表达式中的4个待定常数，将φn代入式(1)可解得受压翼板有效宽度λ

(6)

根据受压翼板有效宽度λ的数学表达关系式，可知c/l与λ/c的关系，以此获取表1数据值。为计算简便快捷，可根据表1通过插值计算出λ。

然后将空间梁格模型的中横隔梁截面翼板宽度换算为有效翼板宽度λ，顶板宽度为2λ+δ。表1中l取边主梁轴线间距，边横隔梁截面参数不变。

此方法只需根据受压翼板有效宽度原理计算出中横隔梁截面翼板的有效翼板宽度λ，然后结合实际横隔梁位置和所计算的截面参数，就可通过有限元软件建立修正后的横隔梁模型。依照此方法对空间梁格模型改进后，将更真实的模拟主梁间的横向联系，预计可更准确的计算主梁结构内力。中横隔梁以及边横隔梁横向联系模型效果图，如图2所示。

1.2 改进空间梁格法的实现流程

该方法的实现流程主要分为3步，图3为整体实现流程图，每一步的操作方法如下。

(1)搭建主梁框架及横向联系。先根据实桥提供的截面参数、材料特性以及结构特征搭建主梁结构框架。接下来对实桥的中横隔梁截面进行处理，利用受压翼板有效宽度原理，将梁格模型的中横隔梁翼板宽度进行等效换算，翼板厚度采用主梁翼板平均厚度t，翼板宽度取有效翼板宽度λ，其顶板宽度为2λ+δ，截面形式如图1所示。梁端边横隔梁截面参数不变，最后添加一个不计自重的材料作为虚拟横梁材料特性。

表1 c/l对应的λ/cTable 1 The c/l value corresponding to λ/c value

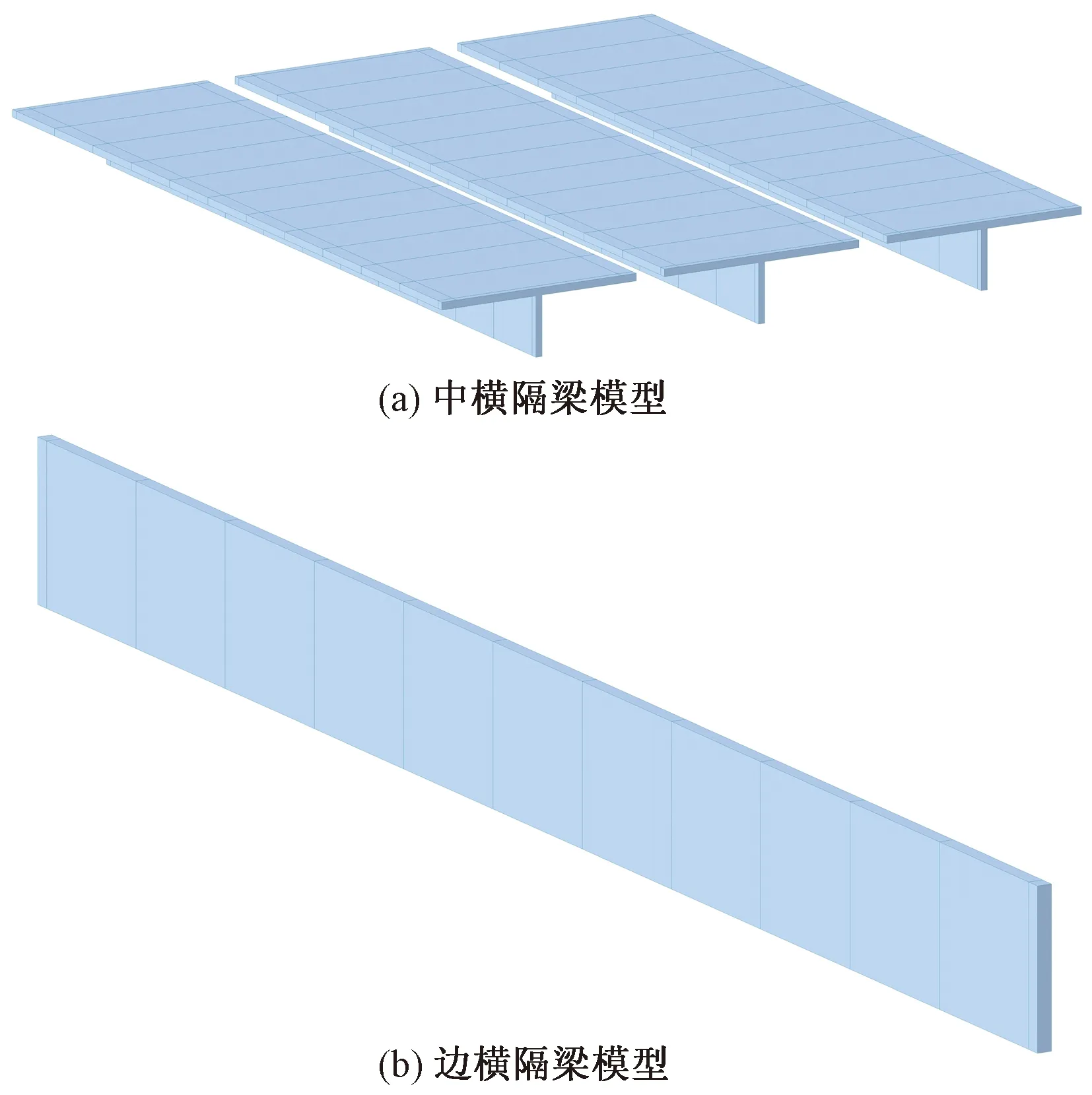
图2 横隔梁模型效果图Fig.2 Transverse beam model rendering

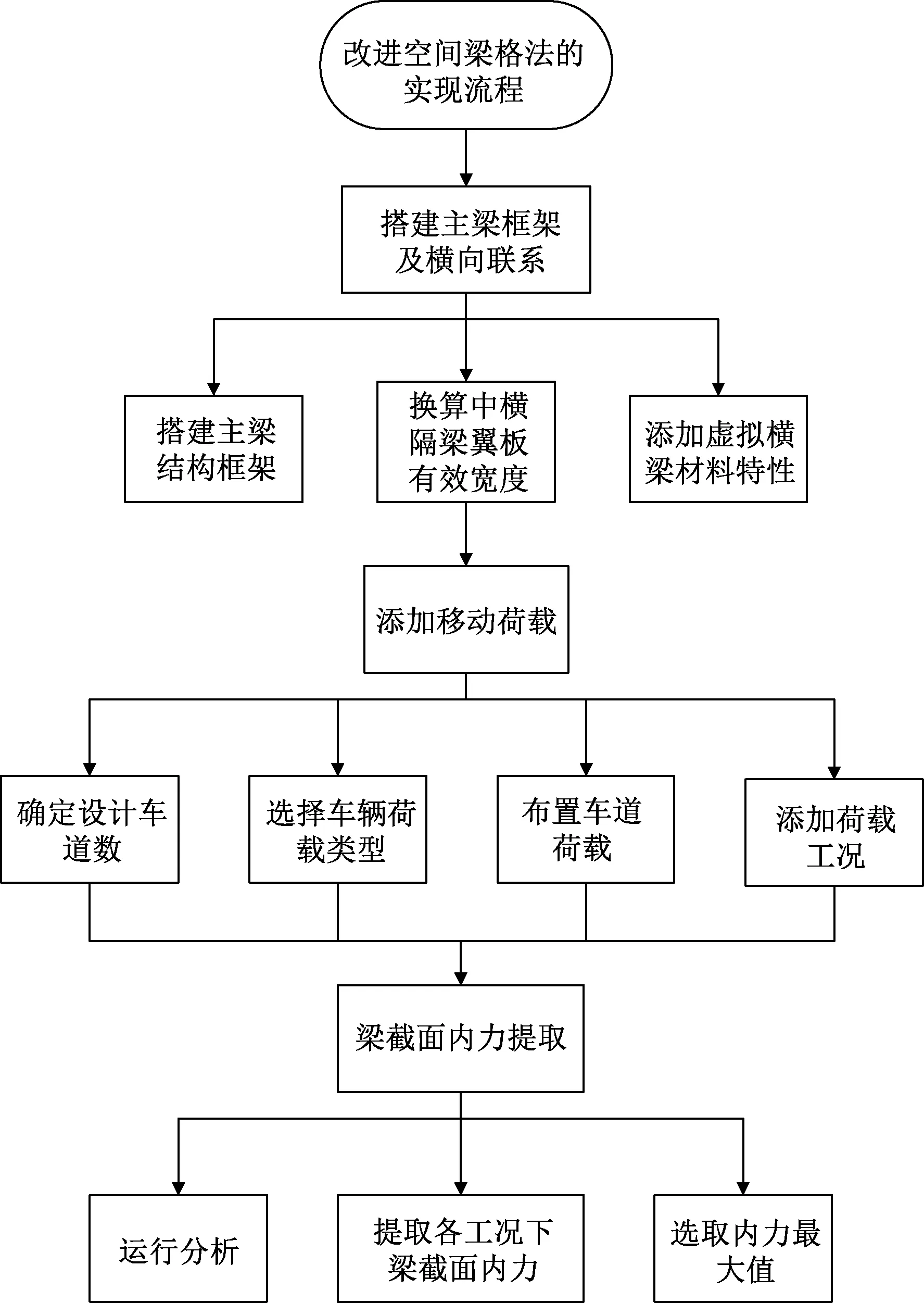
图3 改进空间梁格法的实现流程Fig.3 Implementation flow of improved spatial beam lattice model method

(2)添加移动荷载。根据实桥的设计车道荷载和车辆荷载类型进行移动荷载的添加，其车轮间距一般为1.8 m，横向车辆安全距离一般为1.3 m。然后用3种荷载工况来模拟汽车最不利荷载位置，分别为偏上游加载，跨中对称加载，偏下游加载。

(3)梁截面内力提取。对模型运行分析，分别提取3种荷载工况下的梁截面内力，然后选取3种荷载工况作用下各片梁的内力最大值作为汽车荷载作用下的截面弯矩值。

1.3 改进空间梁格法的优势

空间梁格法利用比拟正交异性板法的原理进行了主梁横向联系的改进，然后再通过三种荷载工况加载来模拟梁最不利受力，操作过程简单快捷。与比拟正交异性板法相比，空间梁格法无需经过手动粗略的查表来完成90个影响系数K1和K0数据的提取，也无需经过冗杂的插值来计算实际梁位处各个荷载位置的K1、K0，在很大程度上缩减了计算主梁结构内力的工作量，更可视化，更精确直观地反映受力后的整体结构响应，提高了工作效率，缩短了桥检工期。

2 算例分析

2.1 工程概况

以4座不同跨径，不同桥宽的装配式预应力钢筋混凝土简支T梁桥为算例，采用两种方法计算汽车荷载作用下主梁跨中弯矩值，将计算结果进行比对，验证本文采用的改进空间梁格法计算宽跨比较大梁桥的主梁结构内力准确性。其中，4种算例的主梁间距均为2 m，纵向设有5道横隔梁，混凝土强度等级C50，双行驶车道，设计等级为公路I级，其他桥况信息如表2所示，单片主梁截面、整体横截面以及纵向横隔梁简图如图4～图6所示。

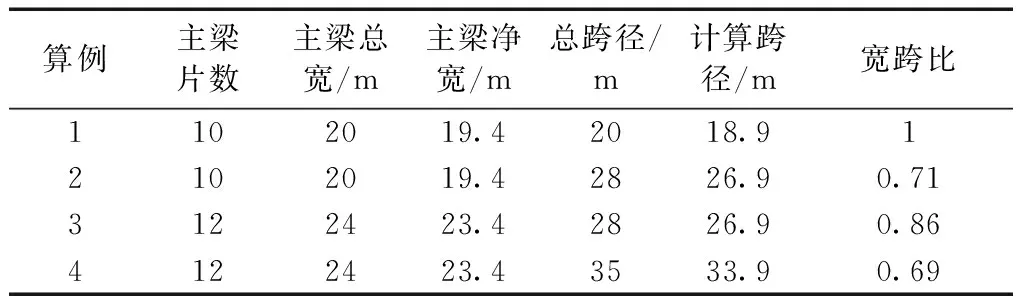
表2 算例桥况信息表Table 2 Bridge condition information table of example

2.2 比拟正交异性板法计算梁跨中弯矩

(1)计算几何特性值。根据工程概况图4～图6可计算得主梁和横隔梁的几何特性值。

(2)查取影响系数K1和K0。根据几何特性计算4种算例的参数θ和α，如表3所示，进而根据文献[8]查阅附表提取90个影响系数K1和K0数据值。

(3)计算各梁横向分布系数。用内插法求实际梁位处的K1和K0，然后可计算得每片梁9个荷载位置处的横向分布影响线坐标值。按照规范要求，不同桥面净宽对应车道的最不利荷载位置布载，通过插值计算可得相应车轮位置处的横向分布影响线坐标值，进而计算各片梁的横向分布系数。

(4)计算梁跨中弯矩。根据式(6)以及规范要求多车道布载的荷载效应不得小于2车道布载的荷载效应的原则，计算得到各片梁汽车荷载作用下的跨中弯矩值，上下幅梁横向分布系数和弯矩计算值对称，仅列出半边各片梁计算结果如表4所示。

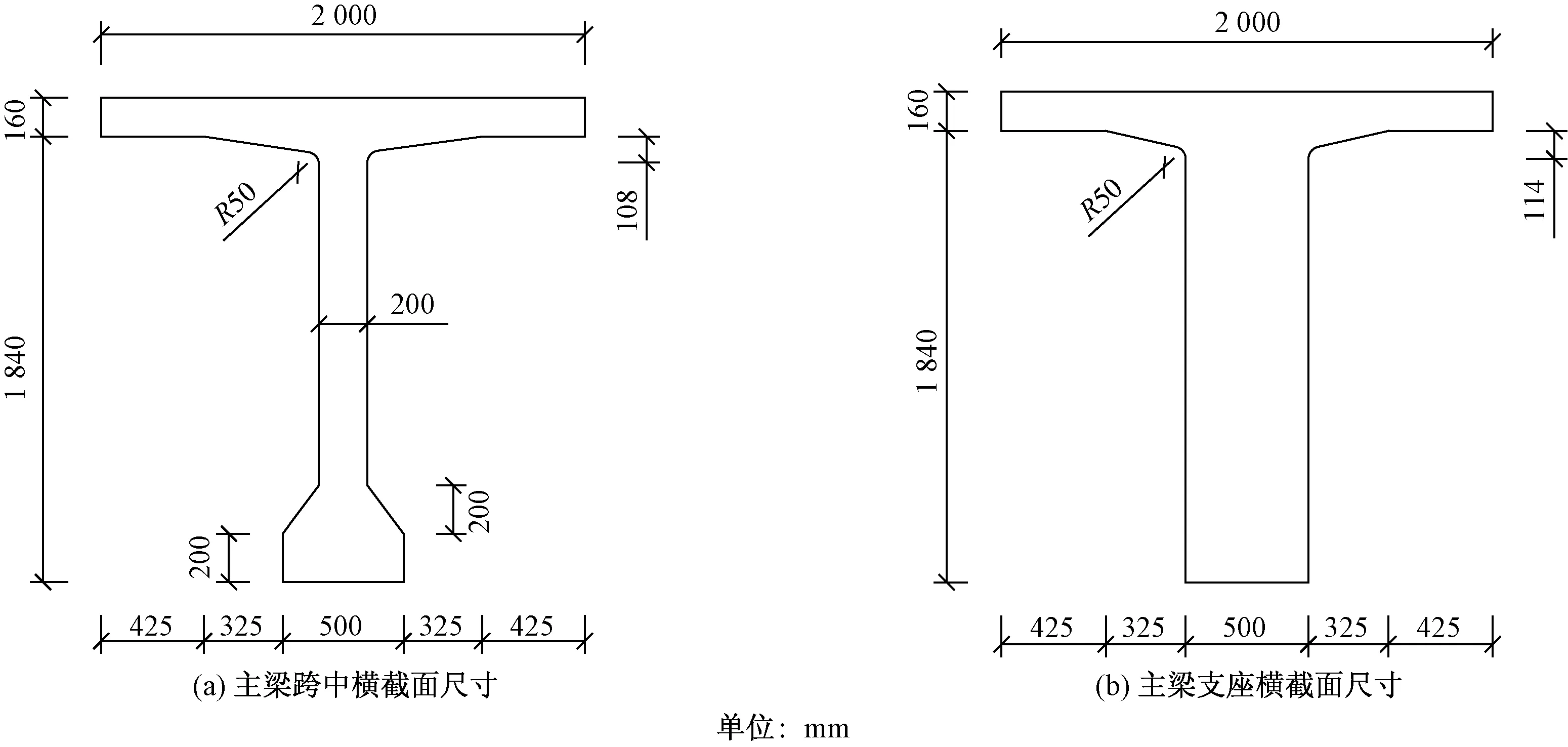
图4 主梁横截面Fig.4 Main beam cross section

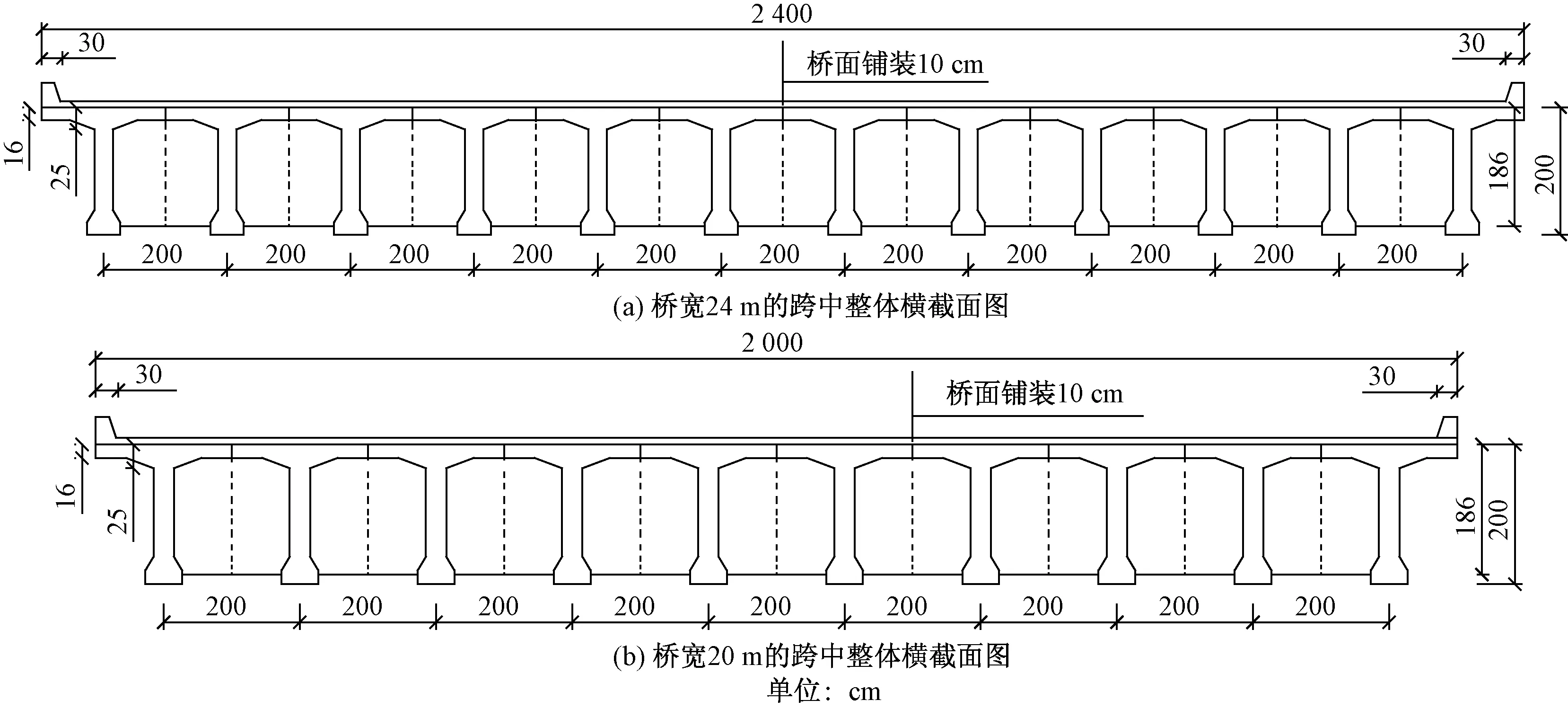
图5 跨中整体横截面图Fig.5 Overall cross section of midspan

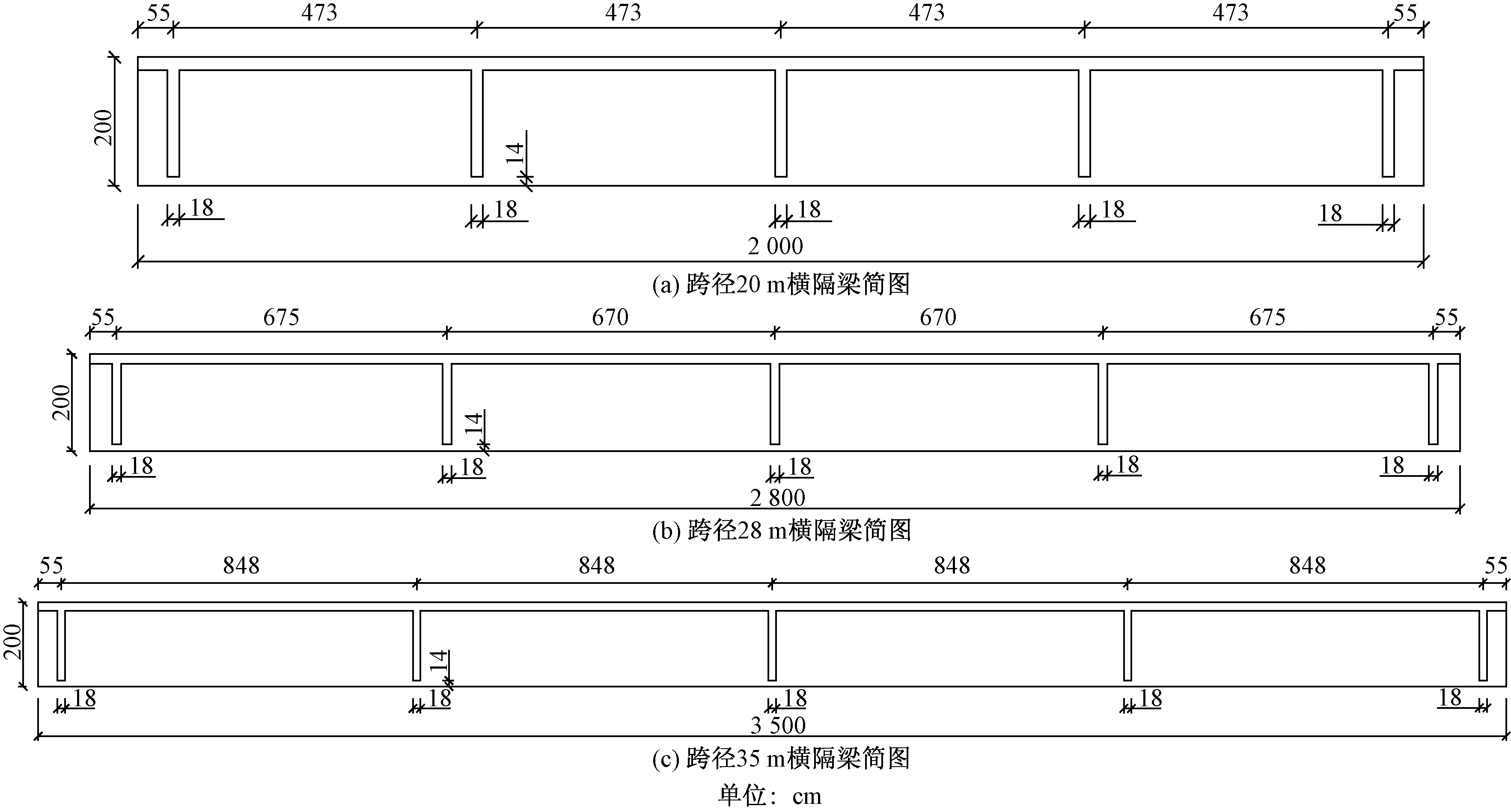
图6 横隔梁简图Fig.6 Diagram of transverse beam

表3 主梁和横隔梁几何特性计算值

(6)

式(6)中：Mq为最大活载内力；μ为汽车荷载冲击系数；ξ为汽车荷载折减系数；mi为荷载横向分布系数；qk为车道荷载中的均布荷载；ωi为均布荷载施加处内力影响线面积；Pk为车道荷载中的集中荷载；y为集中荷载施加处内力影响线坐标。

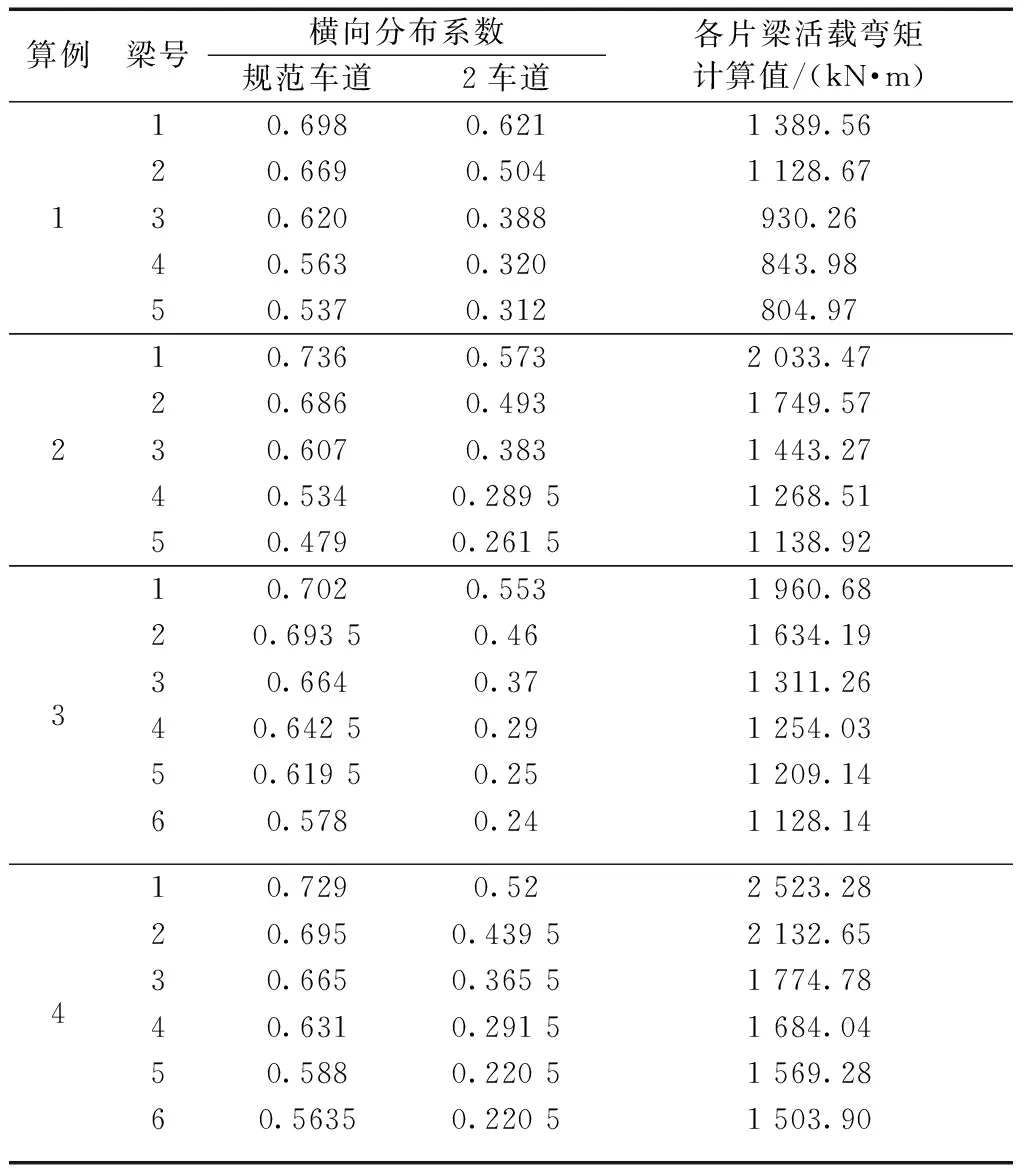
表4 各片梁横向分布系数及弯矩计算结果Table 4 Calculation results of transverse distribution coefficient and bending moment of each beam

2.3 改进空间梁格法计算梁跨中弯矩

2.3.1 搭建主梁框架及横向联系模拟

根据图6可知边主梁轴线间距l和中横隔梁半边翼板宽度c，通过表1可查得中横隔梁翼板有效宽度λ，进而计算中横隔梁的顶板宽度为2λ+δ，横隔梁高度为1.86 m，各算例修正中横隔梁截面参数如表5所示。边横隔梁截面参数不变，其高度为1.86 m，宽度为0.18 m。4种算例修正中横隔梁横截面尺寸如图7所示。根据所得参数，建立空间梁格模型，如图8所示。

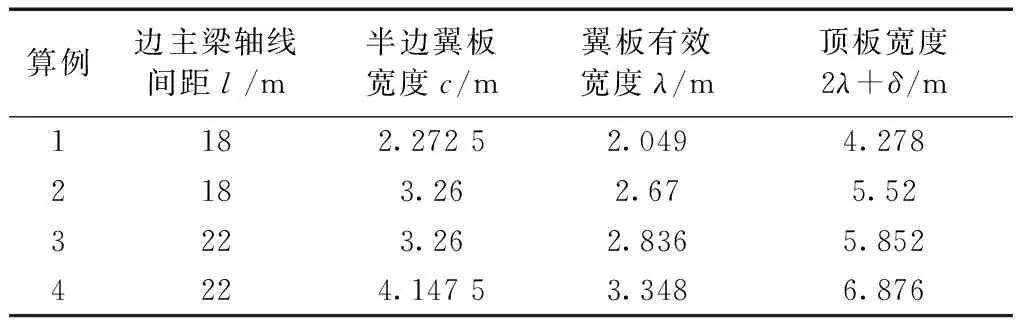
表5 修正中横隔梁截面参数Table 5 Modified section parameters of middle transverse beam

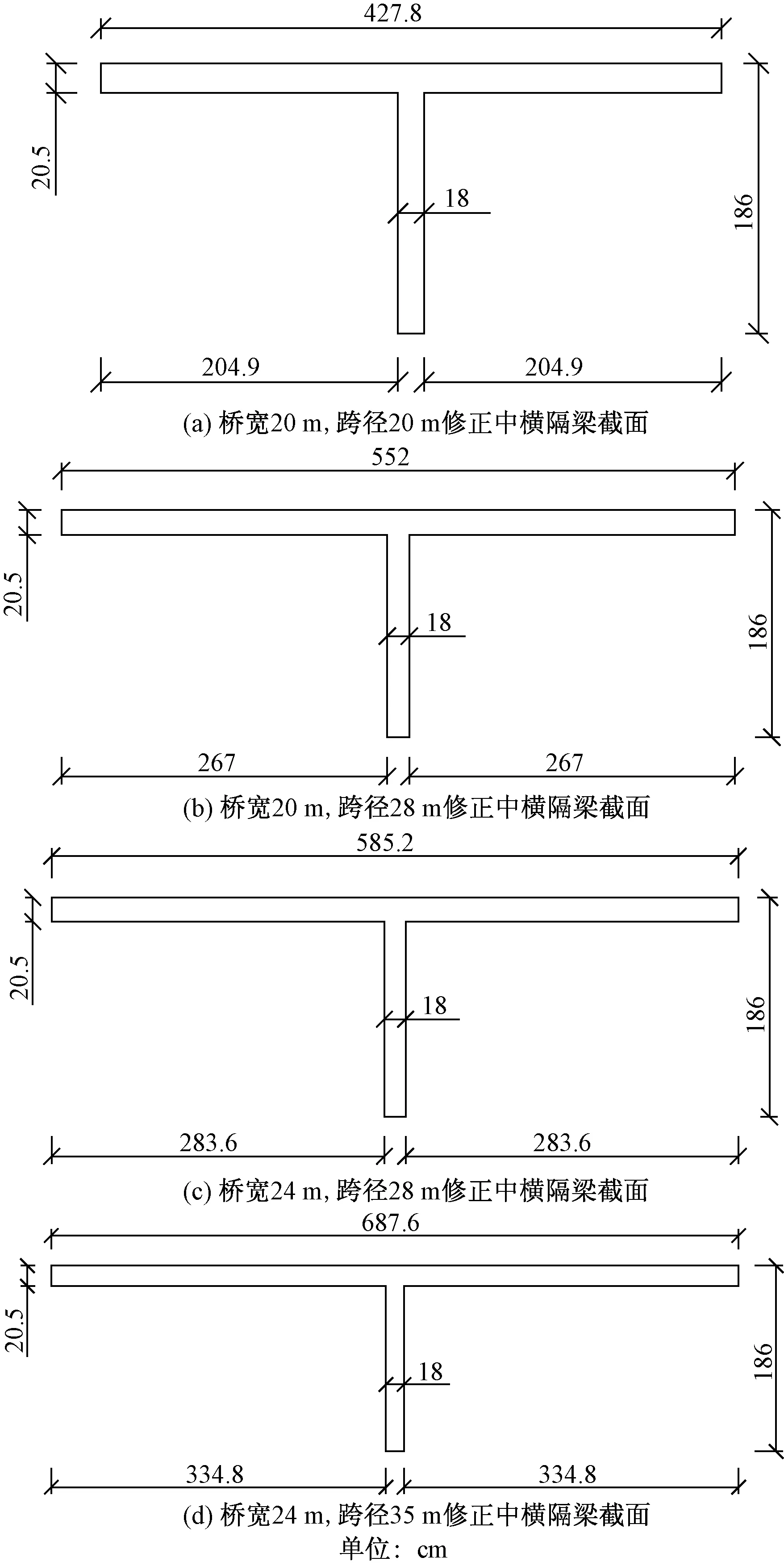
图7 修正中横隔梁横截面图Fig.7 Cross section of middle transverse beam

2.3.2 添加移动荷载

分别按3种荷载工况施加移动荷载，轮距为1.8 m，横向安全距离为1.3 m，车道荷载类型参照相关规范，桥宽20 m横向加载车道为4车道，桥宽24 m横向加载车道为6车道，现列出6车道移动荷载工况示意图，如图9所示。

图8 空间梁格模型Fig.8 Spatial beam lattice model

2.3.3 梁跨中截面内力提取

对主梁单元重新编号，使单元号沿横桥向依次递增，这样可更快速的将各片梁跨中截面弯矩提取出来。然后运行分析，取3种工况下1～10号梁空间梁格法计算的最大弯矩作为其汽车荷载作用下的跨中弯矩值，3种工况提取结果如表6和表7所示。

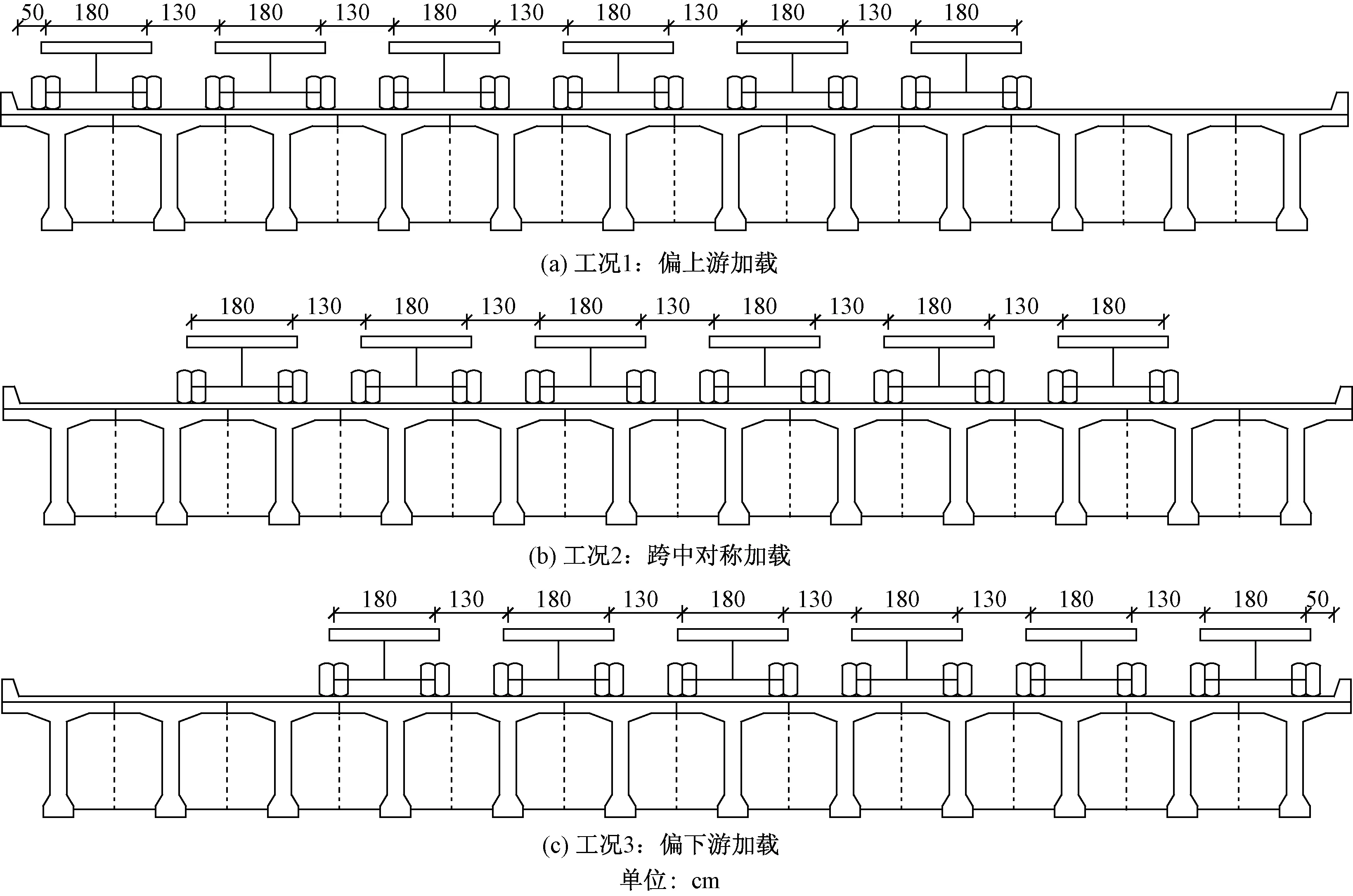
图9 加载工况Fig.9 Loading conditions

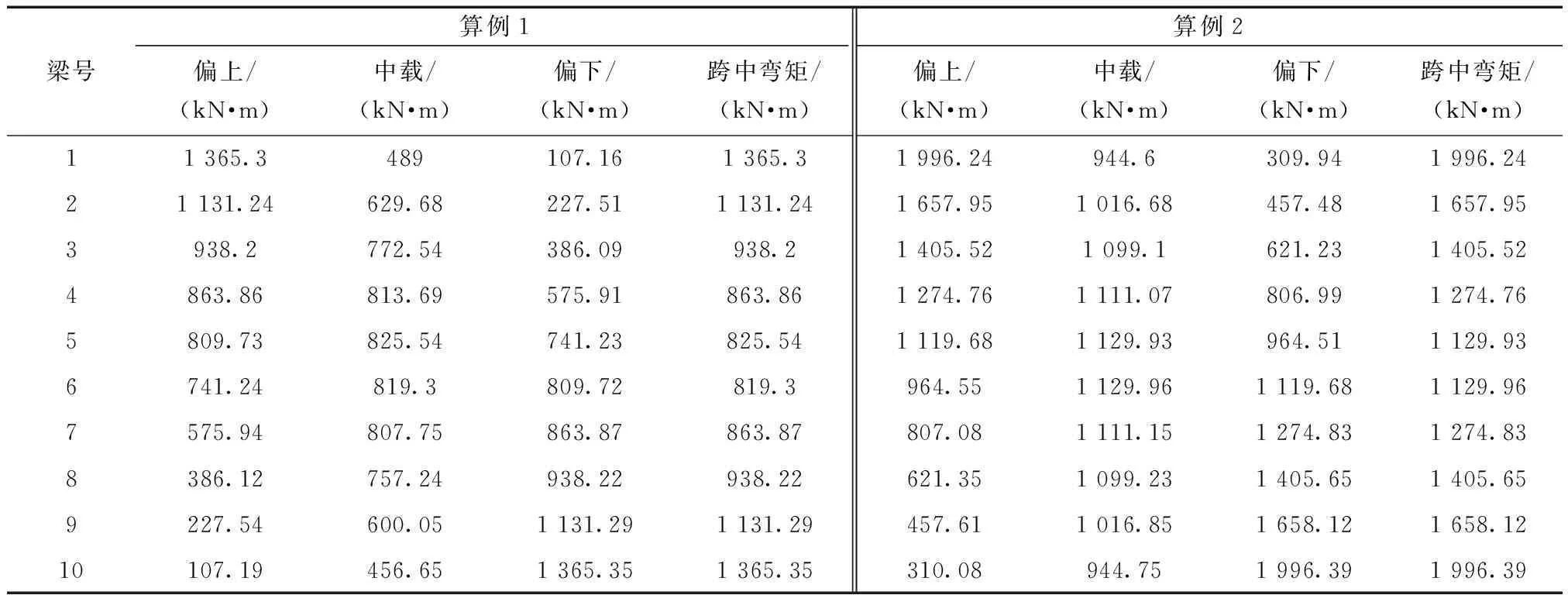
表6 桥宽20 m，跨径分别为20 m和28 m的空间梁格法1～10号梁跨中弯矩值(算例1、2)Table 6 Mid span bending moment of No.1～10 beams of spatial beam lattice model method with bridge width of 20 m and span of 20 m and 28 m respectively (Examples 1 and 2)

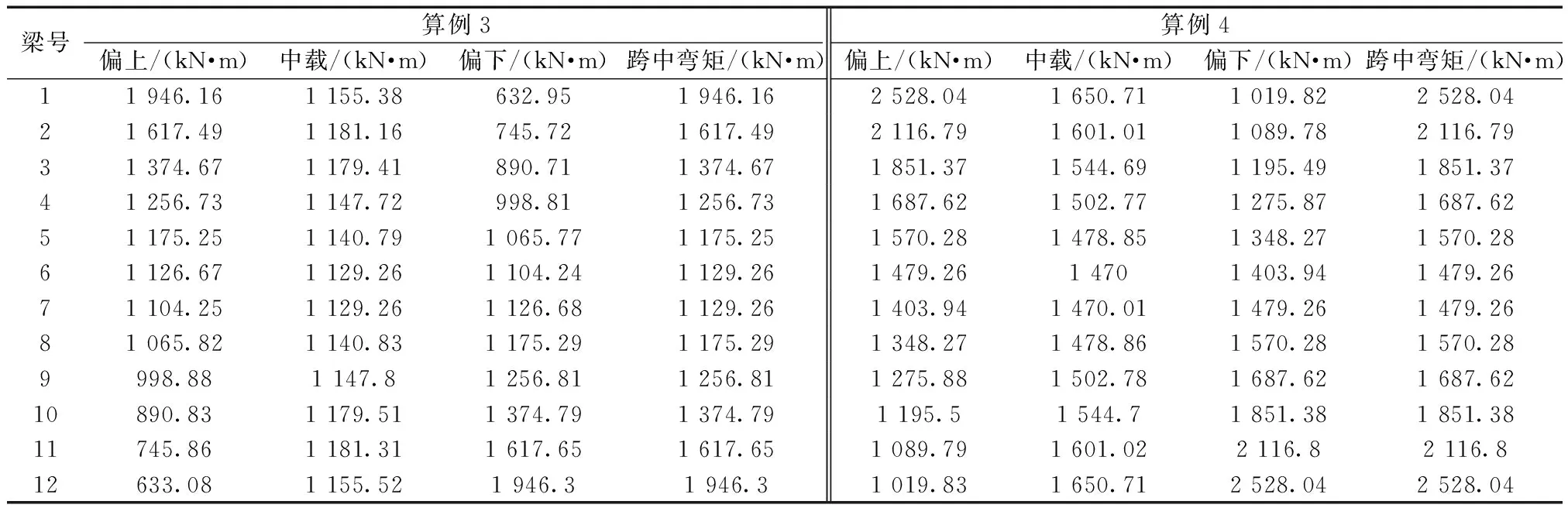
表7 桥宽24 m，跨径分别为28 m和35 m的空间梁格法1～10号梁跨中弯矩值(算例3、4)Table 7 Mid span bending moment of No.1～10 beams of spatial beam lattice model method with bridge width of 24 m and span of 28 m and 35 m respectively (Examples 3 and 4)

2.4 计算结果对比分析

将比拟正交异性板法与空间梁格法对梁跨中弯矩的计算结果进行对比分析，对比结果如表8～表11所示。对比发现两种方法其结果误差几乎均在±5%。说明对于宽跨比较大，多横隔梁以及主梁较为密集的梁桥，可以使用基于受压翼板有效宽度的大宽跨比T梁桥改进空间梁格算法建立有限元模型来计算主梁结构内力。

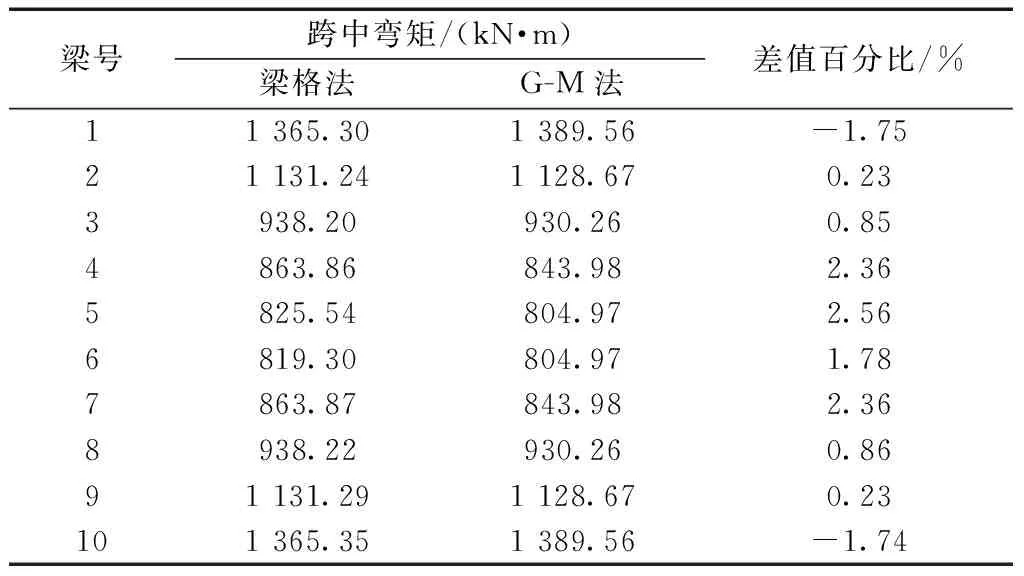
表8 桥宽20 m，跨径20 m(算例1)计算结果对比Table 8 Comparison of calculation results of 20 m bridge width and span of 20 m (Example 1)

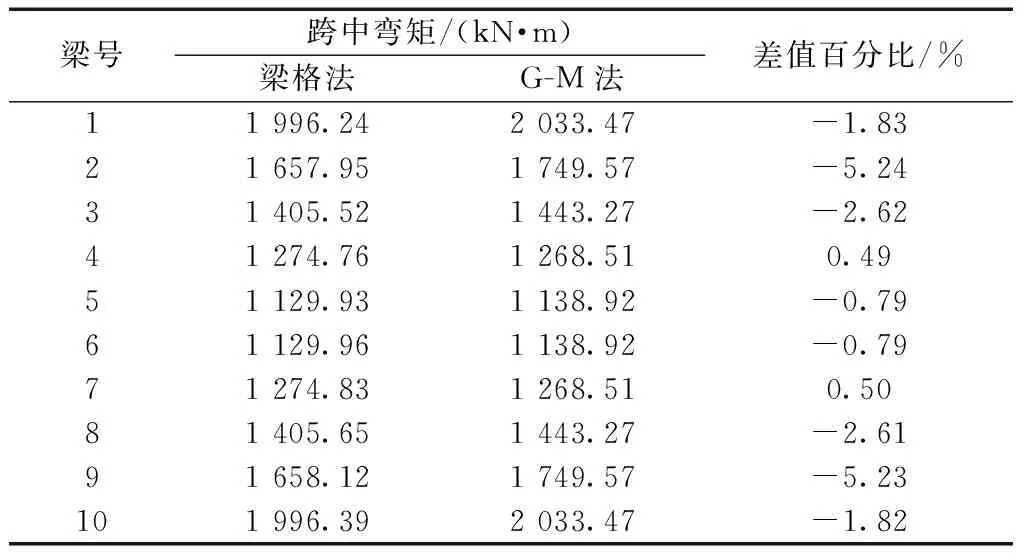
表9 桥宽20 m，跨径28 m(算例2)计算结果对比Table 9 Comparison of calculation results of 20 m bridge width and span of 28 m (Example 2)

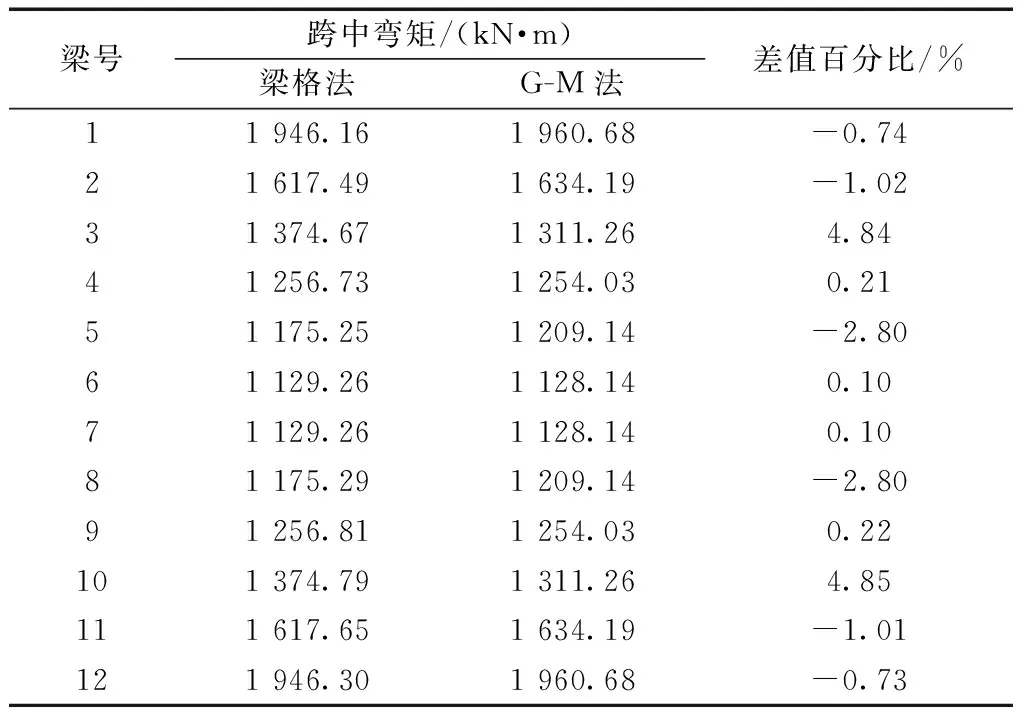
表10 桥宽24 m，跨径28 m(算例3)计算结果对比Table 10 Comparison of calculation results of bridge width of 24 m and span of 28 m (Example 3)

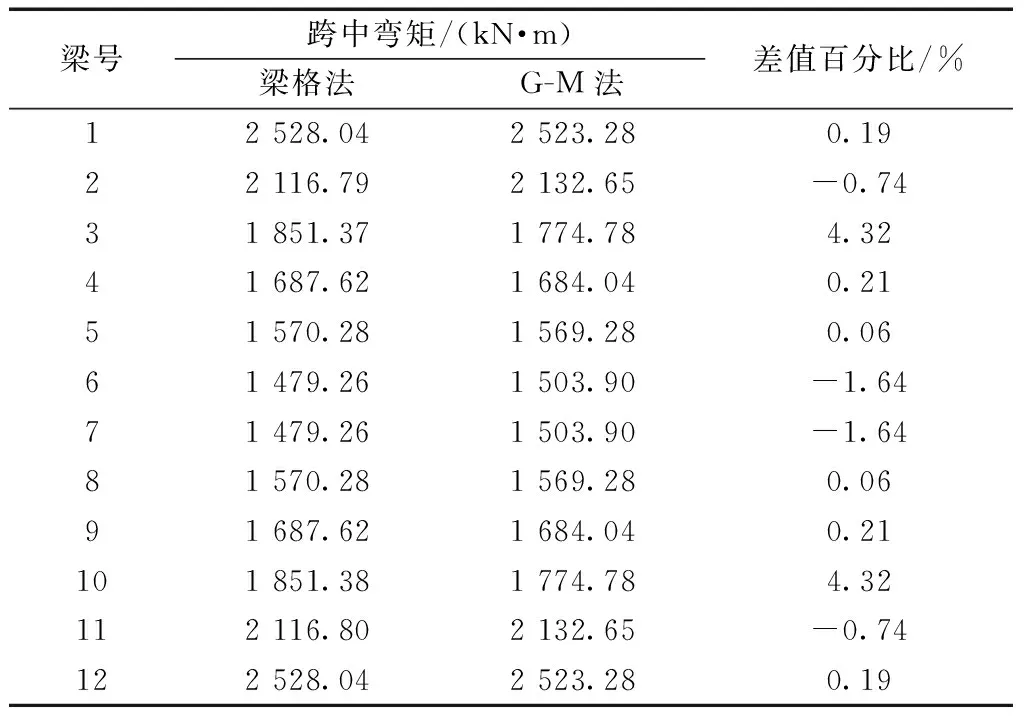
表11 桥宽24 m，跨径35 m(算例4)计算结果对比Table 11 Comparison of calculation results of bridge width 24 m and span of 35 m (Example 4)

3 结论

针对宽跨比较大，多横隔梁以及主梁较为密集的梁桥，提出了基于受压翼板有效宽度的大宽跨比T梁桥改进空间梁格算法计算主梁结构内力，通过方法原理分析以及算例计算对比分析，得出以下结论。

(1)改进空间梁格法计算过程快捷，数据处理简单，不需要进行复杂的插值和查表计算，可以快速提取各片梁任何位置的截面内力，计算结果与G-M法对比，误差在±5%，精度高，误差低，提高了内力计算效率。

(2)改进空间梁格法根据受压翼板有效宽度原理，对横隔梁翼板进行了等效换算，保证了横隔梁对整体结构横向传力作用的准确性，更能真实的模拟整体结构的横向联系，准确计算主梁结构内力。

(3)改进空间梁格法用于桥梁静载试验中，可以更快的计算出各片梁的荷载效率，也可快速计算出不同位置处荷载作用下的变形值作为数据参考，可提高工作效率，使结构内力计算结果更可视化，更能精确直观地反映受力后的整体结构响应。