基于改进Apriori算法的线性代数试卷分析

谢加良，陈艳玲，朱荣坤，宾红华，李 凤

(集美大学理学院，福建 厦门 361021)

0 引言

试卷分析作为教学工作的组成部分，对于了解学生理解和掌握知识的程度，找出教学改革中存在的问题，具有重要的指导作用。试卷分析内容主要包括试卷质量和学生成绩两个方面。有学者基于数理统计的方法，从信度、效度、难度、区分度评价试卷的质量[1-3]，从得分率、平均分、及格率等方面分析考核结果[4]，取得了良好的效果。

为了多维度分析试卷，许多经典的机器学习算法被应用于试卷分析。例如，王平等[5]用聚类算法根据考核数据的相似度将学生聚成不同的类别，针对不同类别学生的特点提出相应的教学策略。孙小雪等[6]采用决策树C4.5分类算法实现海量学生考试成绩精准分类，有效挖掘学生考试成绩中蕴含的有用信息。经典挖掘关联规则的Apriori算法被用于挖掘试题对应知识点之间的关联关系[7-11]，并根据不同的实际需要进一步加以改进。例如，王华等[12]采用改进的Apriori算法挖掘出学生成绩数据中隐藏的课程关联规则。袁路妍等[13]通过减少连接中无效比较的次数来优化Apriori算法，并将其用于挖掘不同课程之间的关联。刘丽娟[14]借助Hadoop技术改进Apriori算法并将其用于挖掘成绩数据。孙国虹等[15]采用基于事务压缩的Apriori算法挖掘大学生成绩预警系统中的数据，从而对课程学习形成有效的预警。这些改进的Apriori算法在一定程度上提升了算法的效率，但都仅采用支持度与置信度进行规则挖掘，无法排除干扰性规则。为了挖掘有效的规则，郭鹏等[16]通过引入兴趣度改进Apriori算法，并用于分析学生的成绩数据，挖掘课程关联规则。刘云翔等[17]利用基于兴趣的Apriori算法分析学生成绩，挖掘课程之间的关联关系。任鸽等[18]引入提升度、兴趣度改进Apriori算法，挖掘不及格课程之间的关联规则。王凤肆[19]运用基于知识点逻辑关系的Apriori算法挖掘出试卷知识点之间的关系，但在算法效率方面仍有待优化与改善。

基于上述分析，本文在经典Apriori算法的基础上引入提升度、兴趣度两个度量阈值来改进规则筛选机制，通过压缩事务数据库、压缩候选集、验证频繁集等方法来优化项集生成步骤。将改进的Apriori算法用于分析线性代数考核数据，挖掘出试卷中隐含的知识关联规则。同时，根据关联规则进一步挖掘课程的核心知识点以及学生的弱项知识点，客观地测评学生知识的掌握情况，为下一轮教学改革提供参考意见。

1 Apriori关联规则算法及改进

1.1 Apriori关联规则算法

关联规则是一种挖掘数据集之间关联性的算法。Apriori算法是经典的挖掘频繁项集的关联规则算法，该算法使用逐层搜索通过连接和剪枝两个过程进行迭代。连接的目的是由频繁k-1项集Lk-1通过连接产生候选集Ck；剪枝的目的是根据Apriori算法的性质剪除Ck中k-1维子集不存在于Lk-1中的项集，从而减少连接时的空间搜索次数。重复连接和剪枝直到不能产生新的频繁项集，得到最大频繁项集。

1.2 Apriori算法的改进

1.2.1 改进规则筛选机制

原算法仅用支持度S、置信度C筛选强关联规则，若设定的最小支持度和最小置信度太小，则会产生无用冗余的规则，而太大则会遗漏有意义的规则。因此，引入提升度L、兴趣度I两个阈值来完善规则筛选机制。

提升度反映了关联规则中的X与Y的相关性，目前普遍采用的提升度计算公式为

其中，L(X→Y)>1表明X与Y呈正相关，L(X→Y)<1表明X与Y呈负相关，L(X→Y)=1表明X与Y不相关。

兴趣度反映了关联规则正负相关的程度。本文采用王桌芳等[20]提出的基于差值的兴趣度模型，记为

其中，I(X→Y)越大于0，说明X与Y正相关程度越高；I(X→Y)越小于0，说明X与Y负相关程度越高。

1.2.2 优化项集生成步骤

原始的Apriori算法存在缺陷：计算支持度时需扫描事务数据库的全部记录；产生大量的候选项集；验证候选项集Ck时需扫描整个数据库。针对上述问题，提出以下优化策略：

(1)压缩事务集：根据最小支持度删除事务集中的非频繁集，避免在计算项集支持度时重复扫描记录。

(2)压缩候选集：根据Apriori算法的性质，若频繁项集Lk-1中项目i的频数小于k-1，则包含i的项集不可能出现在Lk中，所以在连接步前，先删除Lk-1中包含i的项集，以减少可能产生的候选项集的数量。

(3)验证候选集：原算法剪枝时，判断Ck中所有项集的子集是否存在于Lk-1，生成一个Ck需扫描一遍Lk-1。进行改进，剪枝时判断Lk-1的任意项集是否为Ck中项集c的子集，如果是则对c计数，即表示Lk-1包含c的k-1维子集的个数。扫描完毕时，若c的计数小于k则删除Ck中项集c，改进后只需扫描一遍Lk-1。

2 基于改进Apriori算法的试卷分析

2.1 数据准备及处理

选取作者单位2021—2022学年第一学期线性代数期末考试卷面各试题得分情况的数据，共计1 245条。依据同济大学数学系编写的《工程数学线性代数(第六版)》的章节设置，结合线性代数的知识结构及教学主要知识点分布，结合命题教师的出题思想，提取该试卷各试题所考查的知识点，部分试题对应的知识点如表1所示。

表1 试题知识点对应关系

通过分析考查知识点可以发现，该试卷基本覆盖线性代数课程所要考查的内容和教学目标，可以进一步进行知识关联分析。

根据每道试题的得分情况判断是否掌握该试题知识点，将数据转换为0-1型的离散数据，转换规则如下：如果某试题得分大于等于该试题满分的80%，则认为考生掌握该试题的知识点，将其成绩转换为1；如果得分小于该试题满分的80%，则认为考生没有掌握该试题的知识点，将其成绩转换为0。

在Python3.8环境下使用改进的Apriori算法对处理后的数据进行挖掘，经过调试，设定最小支持度为 0.3，最小置信度为0.6，最小提升度为1，最小兴趣度为0.02，执行算法。

2.2 数据挖掘结果分析

2.2.1 试卷知识点关联分析

通过改进的Apriori算法挖掘关联规则，部分有效的强关联规则见表2。以规则1为例分析挖掘出的规则。规则1的支持度为0.43，置信度为0.85，说明当考生答对试题4时，有85%的可能性会答对试题3，由此得出“试题4-方阵行列式的性质/逆矩阵”与“试题3-方阵的特征值”知识点之间具有关联关系。考生在知识掌握的过程中，“试题4-方阵行列式的性质/逆矩阵”是学习“试题3-方阵的特征值”的基础，“试题3-方阵的特征值”的学习能进一步加强对“试题4 方阵行列式的性质/逆矩阵”的知识的理解与掌握。

表2 部分有效关联规则

线性代数以线性方程组为主线，各章节知识点之间关联性强、相互引用的情况多，把握知识点间的关系、构建知识结构体系成为有效教学的关键[21]。通过挖掘结果可以分析某个知识点在线性代数课程体系中的关联关系，以“试题4”作为前项的有效关联规则为例进行分析(表3)。

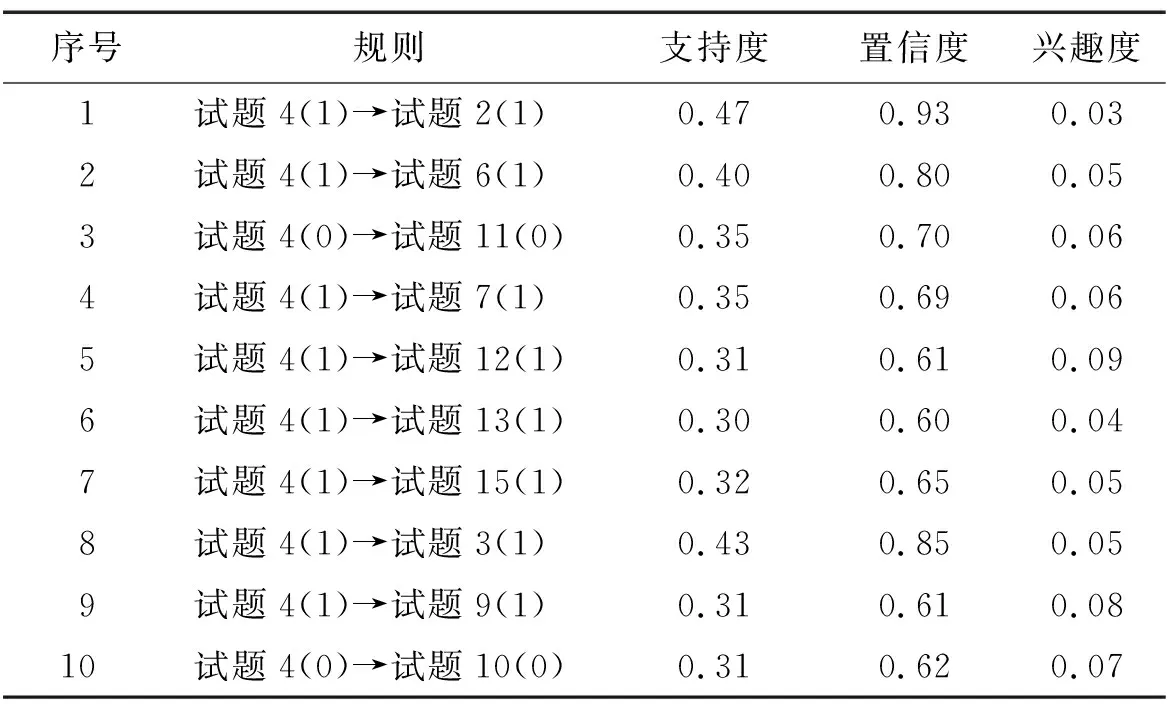
表3 以“试题4”为前项的关联规则

由表3的规则1～规则3可知，“试题4-方阵行列式的性质/逆矩阵”的学习能加深考生对“试题2-矩阵的运算”“试题6-逆矩阵的定义”“试题11-代数余子式的性质”知识的理解。由规则4～规则10可知，考生对“试题4-方阵行列式的性质/逆矩阵”知识的掌握程度，会影响“试题7-矩阵的初等变换”“试题12-矩阵的初等变换”“试题13-线性方程组的解及解的结构”“试题15-行列式的性质/逆矩阵/矩阵的秩”“试题3-方阵的特征值”“试题9-方阵特征值与特征向量”“试题10-向量组的线性相关性”的学习。在线性代数课程中，许多问题可以归结为通过初等变换化阶梯形矩阵，其中涉及线性方程组的求解、特征向量的求法等问题，初等变换包括行列式的变换性质、矩阵和线性方程组的初等变换，掌握行列式变换的基本思想有助于对其他两种变换的学习和应用。可见挖掘结果与线性代数课程体系基本一致。依此类推，可以分析试卷其他知识点的关联关系。

结合试卷提取的知识点，汇总试卷知识点关联规则，构建线性代数知识关联结构图(图1)，分别以15个节点表示试卷中15道试题的知识点，各个节点通过有向线段连接，由规则前项指向规则后项，表示试卷知识点之间的关联关系。

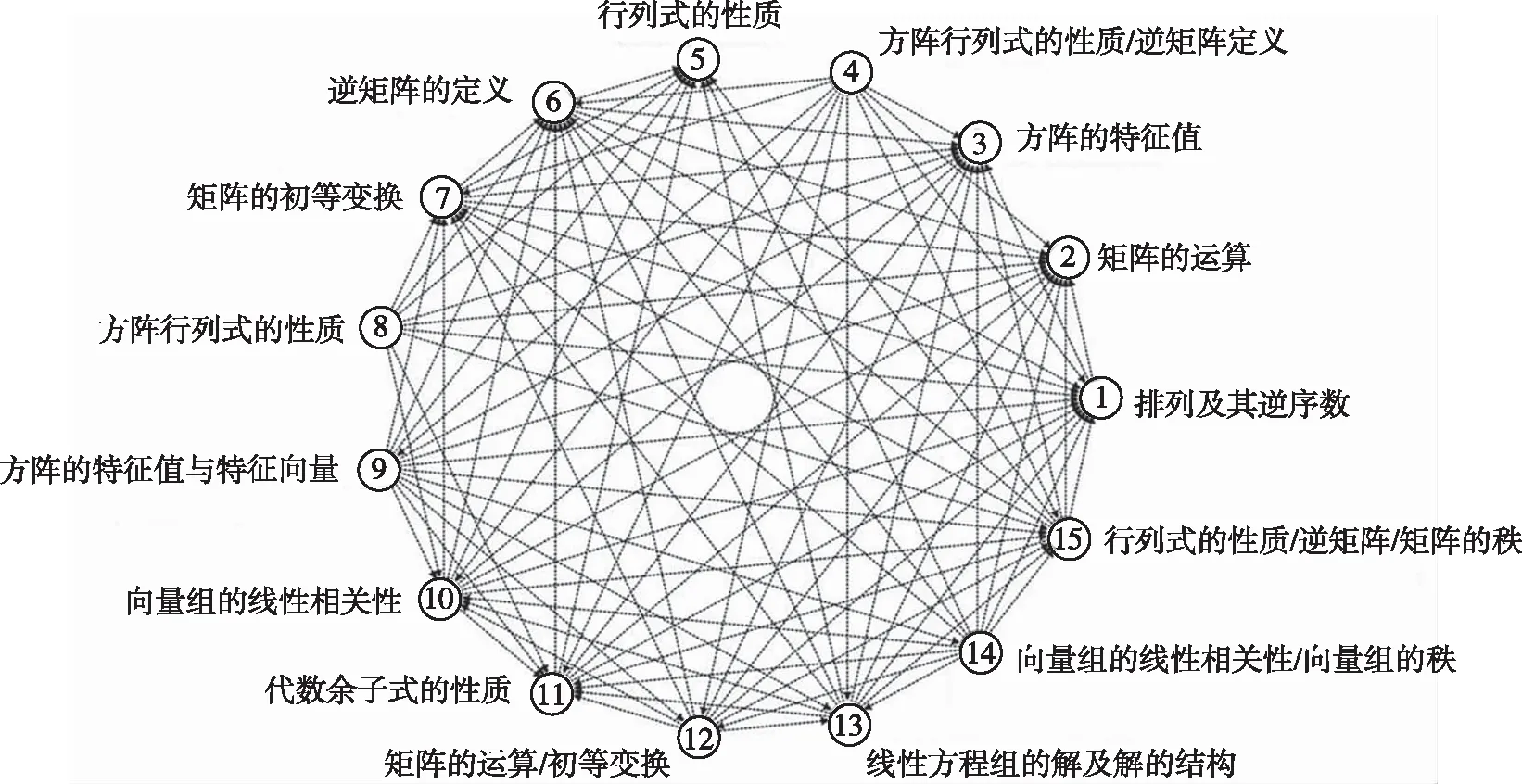
图1 知识关联结构图

根据试卷知识点关联规则，优化线性代数知识点关联图，绘制树型知识关联结构图(图2)，能够更直观地反映初试卷知识点的前后逻辑关系。

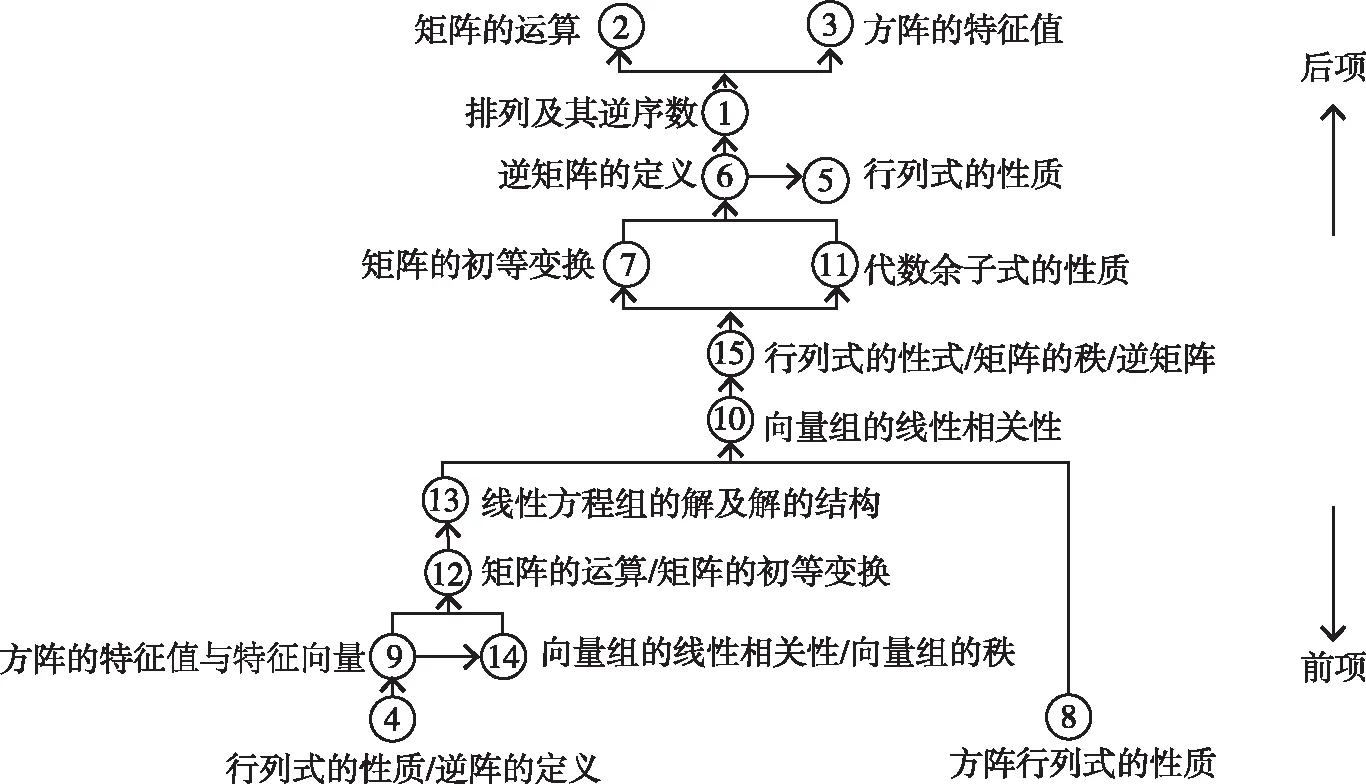
图2 树型知识关联结构图

2.2.2 试卷考核数据分析

根据试卷树型知识关联结构图，结合各试题的得分率，分析考生在线性代数课程的弱项知识点。

2.2.2.1 考生整体知识结构分析

计算1 245位考生组成的整体在各个试题的得分率，根据得分率将知识掌握程度划分为5个等级。整体考生对试卷知识点的掌握情况如表4所示。

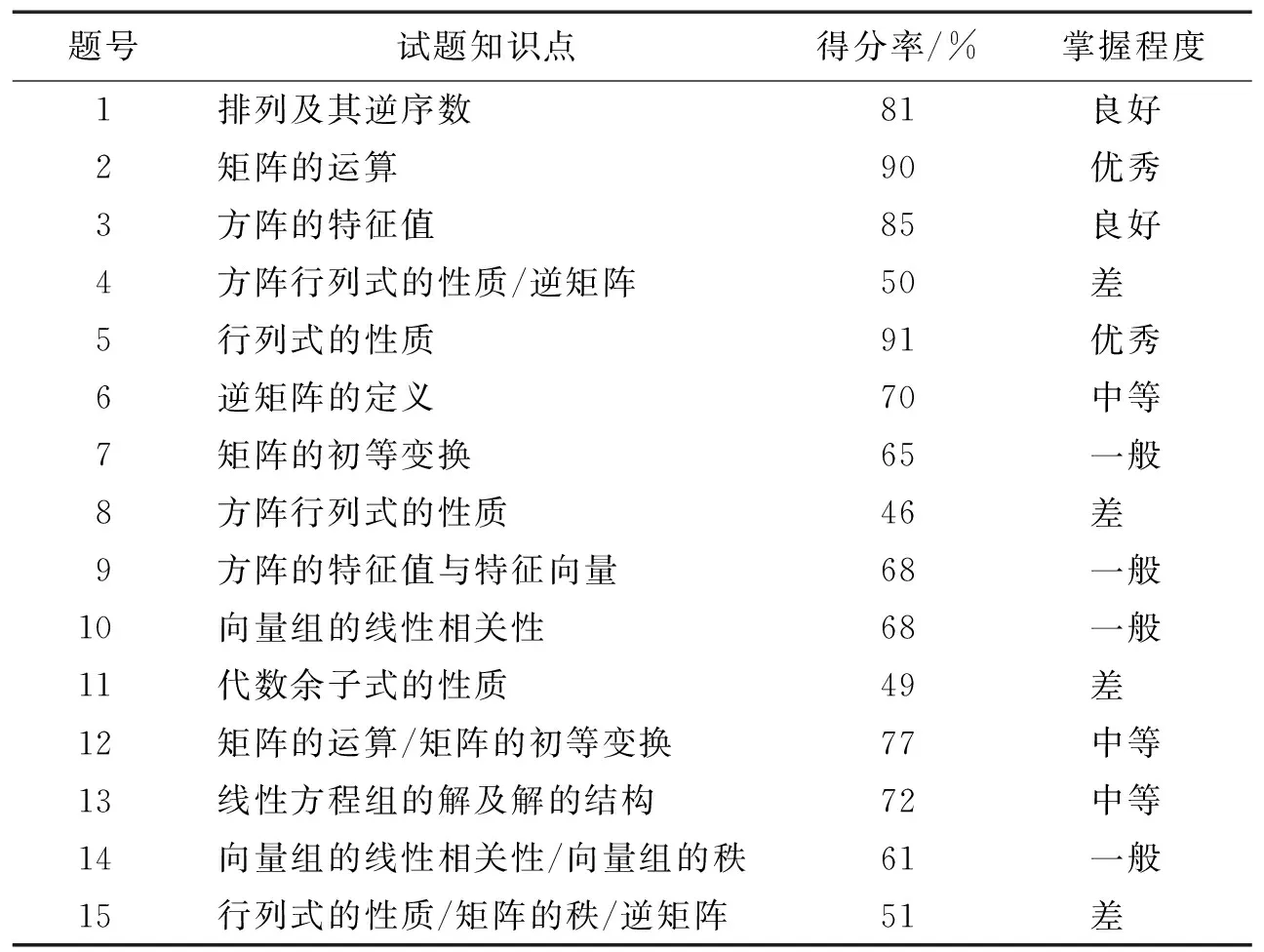
表4 考生整体知识掌握情况

根据考生整体知识掌握情况，依照树型知识点关联图(图2)，梳理考生整体的知识掌握过程。在掌握差的4个知识点和掌握一般的4个知识点中，“试题4-方阵行列式的性质/逆矩阵”“试题8-方阵行列式的性质”掌握差，并且“试题9-方阵的特征值与特征向量”“试题14-向量组的线性相关性/向量组的秩”掌握一般时，会导致“试题11-代数余子式的性质”“试题15-行列式的性质/矩阵的秩/逆矩阵”掌握差，同时会导致“试题7-矩阵的初等变换”“试题10-向量组的线性相关性”掌握一般。因此，考生整体的弱项知识点是“试题4-方阵行列式的性质/逆矩阵”“试题8-方阵行列式的性质”“试题9-方阵的特征值与特征向量”“试题14-向量组的线性相关性/向量组的秩”。

因此，建议教师在讲授“方阵行列式的性质”的内容时，初步培养学生初等变换的思想，为学习矩阵和线性方程组的初等变换做好铺垫。在讲授“方阵的特征值与特征向量”“向量组的线性相关性/向量组的秩”等知识时，增设“方阵行列式的性质”的练习内容，理清初等行、列变换的适用场合，在知识应用过程中深化对初等变换的理解。

2.2.2.2 考生个体知识结构分析

随机抽取1111号考生的线性代数考试成绩，计算该考生在各个试题的得分率，其对试卷知识点的掌握情况如表5所示。

表5 1111号考生知识掌握情况

依照树型知识点关联图(图2)，梳理1111号考生的知识掌握过程。在掌握差的4个知识点和掌握一般的“试题10-向量组的线性相关性”中，“试题4-方阵行列式的性质/逆矩阵的定义”“试题8-方阵行列式的性质”“试题9-方阵的特征值与特征向量”掌握程度差时，会导致“试题10-向量组的线性相关性”掌握一般，进而导致“试题15-行列式的性质/矩阵的秩/逆矩阵”掌握差。因此1111号考生的弱项知识点是“试题4-方阵行列式的性质/逆矩阵”“试题8-方阵行列式的性质”“试题9-方阵的特征值与特征向量”。

因此，建议教师在“方阵行列式”“方阵的特征值与特征向量”的教学中应帮助1111号学生理清初等行列变换的适用问题，例如求矩阵的特征值与特征向量时只能用初等行变换，在其后项知识的教学前布置“方阵行列式”“方阵的特征值与特征向量”的复习任务。建议1111号考生自主增强对“方阵行列式”“方阵的特征值与特征向量”的理解和练习，增强在后项知识中的应用能力。

3 结语

试卷分析评价是教学工作的重要内容，本文从规则筛选机制和项集生成步骤两方面改进Apriori算法，提出一种基于改进Apriori算法的试卷分析方法，并将其用于分析线性代数成绩。经实例验证该算法可以挖掘出试卷中隐含的知识关联规则，对试卷进行总体评价，客观地测评学生知识的掌握情况。同时，根据关联规则进一步挖掘课程的核心知识点以及学生的弱项知识点，从而为下一轮教学改革提供参考意见。这个方法也同样适用于其他学科的试卷分析，具有可推广性和适用性。