Robust optimization of control command for aerospace vehicles with aerodynamic uncertainty

Rui CAO,Yanbin LIU,Yuping LU

College of Automated Engineering,Nanjing University of Aeronautics and Astronautics,Nanjing 210016,China

KEYWORDS Aerospace vehicle;Multi-objective optimization;Polynomial chaos;Uncertain systems

Abstract To reduce the design burden of Aerospace Vehicles (ASVs) control systems,this paper proposes a multi-constrained robust trajectory optimization method,which provides a good front-end input for the control system.Differ from the conventional aircraft,some control performance of ASVs is not only related to the model parameters,but also affected by the flight status.Therefore,the robust optimization method combines this characteristic of ASVs,sets the control performance as one of the optimization objectives,and considers the influence of parameter uncertainty.In this method,the polynomial chaos expansion algorithm is used to transform the trajectory optimization problem with uncertain parameters into the equivalent deterministic robust trajectory optimization problem.Finally,compared with traditional deterministic trajectory optimization methods to illustrate the effectiveness of proposed control optimization method.

1.Introduction

Aerospace Vehicles (ASVs) have broad application prospects and strong research needs,in which hypersonic flight is one of the main defense and space exploration technologies.1This type of vehicle is designed to operate under larger flight envelopes,thus a Turbine-Based Combined Cycle(TBCC)engine is required to fly through these different speed ranges.1,2At present,researchers hope to ensure that the ASVs have good control performance in a large flight range by the control system.3However,the special layout of the fuselage/propulsion integration and the small actuator margin increases its control complexity.4In addition,the wide flight range and uncertainty continue raising the burden on the control system.If only relying on the control system to overcome all the problems and achieve the desired goals,for the control system is extremely difficult or even impossible.According to the Refs.5,6,some control performance of ASV is not only related to the model parameters,but also affected by the flight status.Therefore,the control performance and aerodynamic parameter uncertainty can be considered in advance in the trajectory design stage.Subsequently,the optimization result can be used as the reference control input to the actual control system.In other words,it provides a good front-end input to reduce the control burden,which is of great value for dealing with actual aircraft engineering problems.

Uncertainties faced by aircraft are usually solved by the control system,7the trajectory design only considers the nominal state.8,9However,this work will deal with the influence of some uncertain factors in the trajectory design stage,to balance the burden of trajectory planning and control system design,which is a promising trajectory optimization idea.In this study,uncertainty modeling and propagation are key steps.For nonlinear dynamic systems,Monte Carlo (MC),10Markov chain,11unscented transform,12Fokker-Planck-Kolmogorov framework,13and Polynomial Chaos (PC)14can be used to quantify the uncertainty caused by uncertain variables.The MC method is popular because of its ease of implementation,but its computational cost precludes its application in robust optimization.Recently,the PC method has gained much attention since it can provide accuracy comparable to the MC method at a significantly lower computational cost.Methods based on PC Expansions (PCE) have been applied to various disciplines in aerospace engineering,including aerodynamics,15airfoil design,16coupled aerodynamics-structure analysis,17,18and flight dynamics.14,19,20

In the field of aerospace engineering,the study of stochastic dynamic systems mainly focuses on effective algorithms for uncertainty propagation.14,19,20Only a few studies on optimization design of uncertain dynamic system,which can be found in Ref.21 and Ref.22.With the emphasis on trajectory robust optimization problems,the research on this aspect increases.Ref.23 and Ref.24 used the PCE method to transform the original stochastic trajectory optimization problem into an equivalent deterministic one in the expanded higherdimensional state space,then adopted the pseudo-spectral method to optimize the augmented deterministic system to obtain a robust optimized trajectory.In Ref.25 and Ref.26,the non-intrusive PCE scheme was employed to optimize the airplane trajectory with uncertain aerodynamic parameters.Jin et al.27combined the genetic algorithm and the MC method to solve the uncertain rendezvous and proximity operations in perturbed elliptical orbits.Ref.12 and Ref.28 were based on the unscented transformation method to solve the stochastic ascent trajectory optimization problem for a twostage,semi-reusable space launch system.Grant and Bolender29proposed the higher-order stress cases to capture the worst-on-worst set of dispersions obtained by MC simulation,and achieved robust optimization by optimizing the worst-case scenarios.Flanzer et al.30used mutually orthogonal random uncertain parameter combinations on nested sparse grids to calculate trajectories,and then obtained the mean and variance of these trajectories to perform robust optimization.Richter and Holzapfel31designed stochastic collocation to obtain the mean and standard deviation of uncertain state,then used the pseudo-spectral method to minimize the statistical information to calculate the best flight trajectory.

In the research of robust trajectory optimization by the aforesaid researchers,the oriented system is a 3 Degree-of-Freedom(DOF)point-mass model instead of the 6DOF model used in actual flight control.In the trajectory optimization problems based on 3DOF point-mass model,the Angle-of-Attack (AOA) is often the control variable.If the optimal AOA history is without the reasonable boundary and variation rate,then the controller is difficult to track the desired trajectory.This leads to the question that whether the resulted optimal trajectory is actually controllable.In addition,3DoF trajectory optimization is difficult to set the control performance as one of the optimization objects,because it cannot provide the transfer function of the elevator to the angle of attack/pitch rate.To solve these problems,we have carried out the work of this article.Considering the multiple constraints and uncertainties of ASVs,based on the 6DOF longitudinal model,a multi-constraint robust trajectory optimization method is proposed.Moreover,the optimization method takes some control performance as one of the trajectory optimization objectives to ensure that the aircraft still has good performance under the uncertain aerodynamic parameters.Thus,the optimal trajectory obtained by this method has good robustness and control performance under open-loop conditions.

The remainder of this paper is organized as follows:In Section 2,the kinematics model and dynamic analysis of ASV are introduced.In addition,a deterministic trajectory optimization problem considering control constraints is proposed.Subsequently,an implementable computational model of robust control command optimization for uncertain systems is presented in Section 3.In Section 4,the effectiveness of augmented system based on PCE to describe the uncertain system is analyzed.Furthermore,the designed robust optimization method and the conventional optimization ideas9are respectively applied to the ASV nonlinear system to verify the effectiveness of designed method in this article.Section 5 concludes the paper.

2.Problem statements

2.1.Model analysis of aerospace vehicle

This paper takes the Generic Hypersonic Aerodynamics Model Example (GHAME) vehicle as the research object32for subsequent analysis and simulation.The outline layout of GHAME is shown in Fig.1.The longitudinal dynamics of ASVs can be described as the following nonlinear differential equations:

Fig.1 GHAME vehicle configuration.32

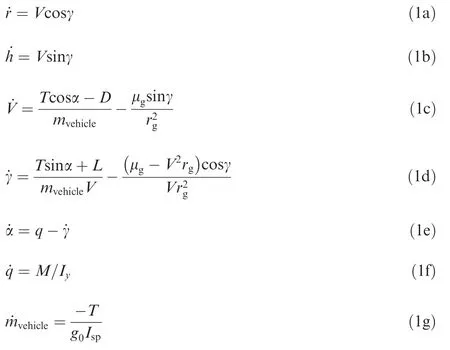
whereV,γ,α,qdenote the flight speed,flight-path angle,AOA and pitch angle rate,respectively.randhrepresent horizontal displacement and altitude of ASV.mvehicleindicates the vehicle weight andIyis the inertia moment.Ispdenotes the specific impulse.vehicleis the fuel mass flow rate.g0is the gravitational acceleration of the earth surface.μgexpresses the gravitational constant,rgis the earth radius.L,D,TandMrepresent lift,drag,thrust and pitching moment of GHAME,respectively.

Similarly to what was done in Oscar et al.,33approximations of the forces and moments to be employed for trajectory design have been derived as follows:

where

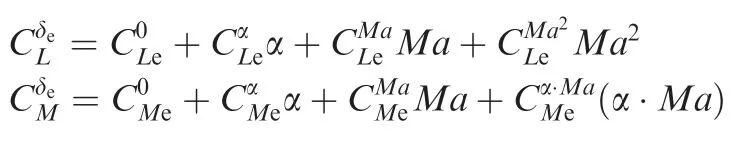
δerepresents elevator deflection,Mais the Mach number,qdenotes dynamic pressure,andSrefexpresses the vehicle reference area.

The engine model is shown in Eq.(3).34The fuel/air ratio of engine is adjusted to stoichiometric ratio,which is 0.029φF.ThrustTis a function of the Fuel Equivalent Ratio (FER),AOA,and Mach number

where φFis the FER,ρ denotes the atmospheric density,Acrepresents the inlet airflow capture area.The expressions ofIspand capture-area coefficientCTare as follows:

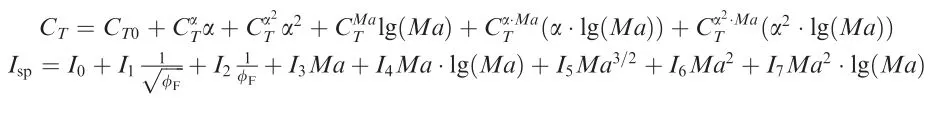
The ranges of the above aerodynamic and propulsion coefficients are at the flight conditions with Mach numberMa∈[0.4,24]and angle of at tack of α∈[-3o,21o].

2.1.1.Model constraints

Due to the complex structure and flight environment,the actuators and flight status of ASVs would be more restricted.The main constraints are shown in Eq.(4).Here,the upper bound constraint of AOA is mainly restricted by the condition of inlet unstart.FER is subject to a state-dependent constraint,which defines the operability of the scramjet engine.The remaining control input δeis restrained by the physical limitations in the elevator deflection.

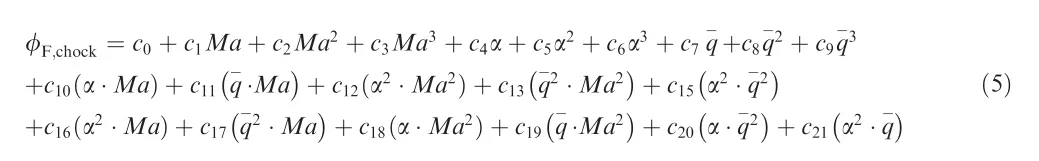
where the coefficients for φF,chockcan be referred to Ref.34.

Fig.2 shows that the variation of back pressure ratio with α at differentMa,which gives the AOA boundary of the hypersonic inlet unstart.35The boundary is numerically fitted to obtain the AOA constraint as shown in Eq.(6).

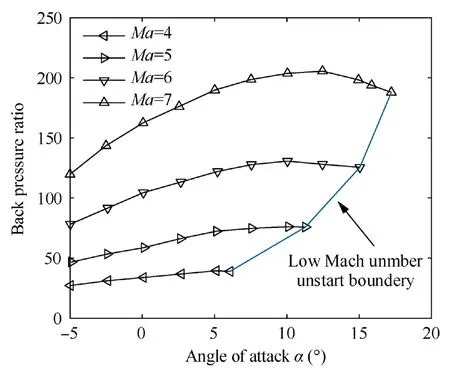
Fig.2 Effects of Ma and α on back pressure ratio.

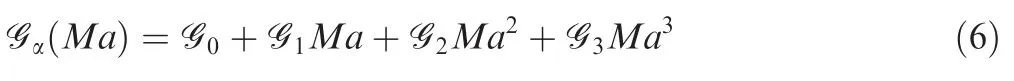
According to Eqs.(5)–(6),it can be seen that FER is affected by AOA,and the AOA is also limited by the engine state.Meanwhile,the engine inlet pressure would cause the pitch moment change,thereby affecting the AOA.This shows that there is a coupling effect between the AOA and the FER,which makes the constraint relationship of ASV more complex.In addition,due to the aerodynamic coefficient uncertainty,the constraint boundary would be more unclear,which further increases the design difficulty of the control system.

2.1.2.Hypersonic model analysis

ASVs not only have the complex nonlinearity and constraint that conventional aircraft do not,but also possess different longitudinal motion characteristics.This unique flight characteristic may contribute to the trajectory planning and controller design of ASVs.

According to Ref.2,different from the low-speed flight,although the angle of attack is a short-period state during high-speed flight,it also is affected by long-period motion state(such as flight speed,altitude).In other words,in the case of high-speed flight,the velocity and altitude of vehicle will affect the angle of attack motion.Moreover,for ASVs,the aerodynamic derivatives are no longer constants,and the variation of atmospheric density cannot be ignored.Therefore,the flight performance of ASVs is not only related to model parameters,but also affected by flight trajectory/status.5,6And Ref.7 also illustrates this.

Based on the above contents and the conclusions of related researchers,the relationship between control performance,aerodynamic parameter,and flight trajectory is summarized,as shown in Fig.3.

According to Fig.3,the variation of aerodynamic parameter would affect the nominal trajectory,then the change of Mach number and dynamic pressure caused by the trajectory would also impact the current aerodynamic coefficient.Moreover,the aerodynamic derivatives (∂CM/∂α（V）,∂T/∂h,∂T/∂V,etc.) related to the control performance are correlated with the flight speed and altitude,so they are also affected by the flight trajectory changes.Therefore,the coupling relationship of ASVs may bring about the complexity of controller design.However,from another perspective,it gives a hint that trajectory can affect some control performance of ASVs.

Fig.3 Diagram of influence relationship.

To have a more intuitive display,the influence of flight trajectory on Short-period Damping-Frequency(SDF)characteristic of ASVs is analyzed.Considering that the vehicle climbs along with the constant dynamic pressure in the range of 30 kPa-120 kPa,and then several points on each isodynamic pressure trajectory are selected to analyze the corresponding SDF characteristic.Fig.4 shows the distribution of SDF characteristic on different dynamic pressure trajectories.Among them,the relevant levels (Level one,Level two,etc.) are divided according to the flight quality manual.36

According to Fig.4,it can be seen that this characteristic of ASVs would change with the flight Mach number and dynamic pressure (or altitude).Therefore,it is reasonable to consider this feature in the trajectory optimization objective.In other words,the control performance greatly affected by the trajectory can be regarded as one of the objective functions for trajectory optimization.On this basis,this work improves the traditional optimization problem,so that some control performance is considered in the trajectory design stage.

Fig.4 Short-period damping-frequency distribution diagram of GHAME along the trajectory.

2.2.Trajectory optimization problem of ascent phase

2.2.1.Traditional trajectory optimization problem

The general form of a deterministic dynamic problem,which can be written as follows25.Find u（t）,makes

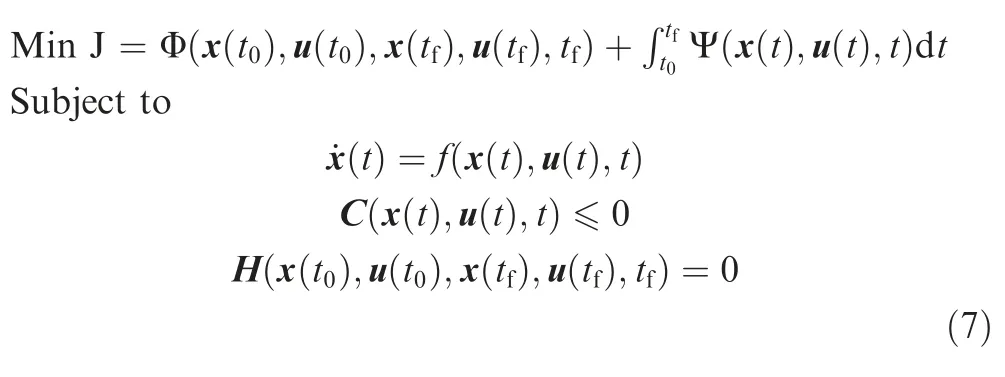
wheretis the time,x denotes the state vector,u（t）represents the design variable,C ∈is the path constraint,and H ∈is the boundary constraint.Φ（·）represents the terminal optimization form,Ψ（·）dtrepresents the integral optimization form.Generally,the design variable u in optimization problem(7)is AOA.Moreover,the performance indexJis the shortest time,the minimum fuel consumption and so on,does not involve the control performance.

2.2.2.Trajectory optimization problem considering control performance

Different from the conventional optimization problem (7)using AOA as a design variable,δeand φFare taken as design variables in the trajectory optimization method proposed in this paper.Hence,it can provide the corresponding reference control input for the actual controller,and also lay the foundation for introducing control performance into the trajectory optimization problem.

Since the aerospace vehicle is usually designed to be statically unstable,short-period performance (damping-frequency characteristics) must be guaranteed first in control.In addition,compared with anti-interference performance,tracking performance,and control feasible region,the SDF characteristic is more affected by trajectory.Therefore,in the trajectory optimization method of this paper,this control performance-the SDF characteristic is mainly considered as one of the optimization objectives.The short-period ideal model with a level-one Flying Quality (FQ)36is shown below:wheresindicates differential operator,Kq=1,Tθ2=0.7143,ζsp=0.707,ωsp=3.5.≡qis the pitch angle rate,ζspand ωspare the damping ratio and natural frequency.

Ref.36 gives a function to measure the similarity of two systems in the frequency-domain,namely the mismatch function.The smaller the value of mismatch function is,the higher the similarity between the two systems is.Therefore,based on this concept,Eq.(9) is given to measure the similarity of frequency-domain characteristics between complex highorder systems and ideal model (8) with level-one FQ,so as to indirectly estimate the SDF characteristic of ASVs.

The smaller the value of Eq.(9),the higher the similarity between the two systems,which means that the frequency domain characteristics of complex systems are closer to the ideal model(8),that is,its SDF characteristic are better(closer to the level-one FQ)under open-loop.Consequently,the SDF characteristic can be introduced into the optimization objective by minimizing Eq.(9).

whereGandPcorrespond to the amplitude and phase of systems.ωiis the frequency of interest and is chosen within the range [1,10]rad/s in this paper.The subscript H denotes the complex system,the subscript S represents the ideal model(8),andKindicates the weighting factor,which is chosen as 0.01745.2,5,36

In addition,the target position and the fuel consumption are also considered.Then,the optimization objective is to minimize the errors between terminal position（rf,hf）and target position（rT,hT）,the fuel consumption,and theJSDF,namely:

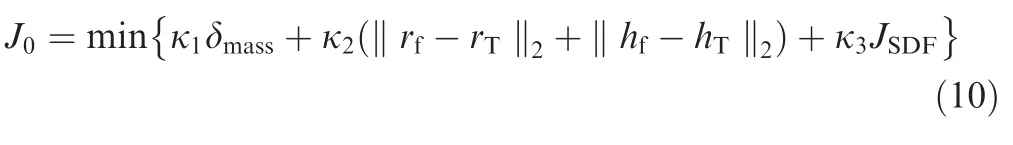
where δmass=mvehicle（t0）-mvehicle（tf）,the subscript f represents the terminal state of variable.κ1,κ2and κ3are the weight,which are set by the user.

The next stage of ascent phase is the cruise phase or the separation window of the two-stage to orbit vehicle.This means that the terminal state of ascent phase is also the initial state of cruise phase or separation window.Therefore,it is necessary to set the terminal constraints of ascent phase according to the predetermined mission requirements.In general,the following constraint inequalities are adopted:

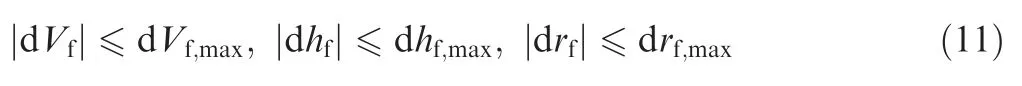
where |dVf|,|dhf|,and |drf| are the errors of velocity,height,and horizontal displacement between the terminal and the target,respectively.dVf,max,dhf,max,and drf,maxare the corresponding allowable error thresholds.

According to the previous discussion,the trajectory optimization problem of ascent phase in this paper can be expressed as the following Optimal Control Problem (OCP):

Remark:Problem (12) belongs to the deterministic trajectory optimization problem,that is,the influence of parameter disturbance or initial value uncertainty on the resulted trajectory is not considered.

Under this optimization result obtained by solving the problem (12),once the aerospace vehicle is affected by uncertain perturbation or interference,it will easily deviate from the pre-designed optimized trajectory and be difficult to satisfy the expected constraints.If the influence of parameter uncertainty is considered in trajectory optimization,the resulted nominal trajectory has good robustness to the uncertainty.Furthermore,it can provide a feedforward input with better performance to the controller,thus balancing the burden of trajectory planning and control system design.

Consequently,in the next section,the PCE method is introduced to quantify the uncertainty of system and constraint,so as to update the deterministic optimization problem(12)to the robust optimization problem considering control performance.Finally,this optimization problem is solved to complete the robust optimization design of ascent trajectory.

3.Robust optimization scheme for ASVs

In this section,based on the PCE method,the process of converting an uncertain dynamic system into an equivalent deterministic dynamic system in an expanded higher-dimensional state space is introduced.Besides,a robust control command optimization method is proposed.

3.1.The quantification process of uncertain system

3.1.1.Equivalent deterministic differential equations based on PCE

Considering that the aerodynamic of GHAME has uncertain information Δ:

wheretrepresents the system time,x=[r,h,V,γ,α,q,mvehicle]∈Rn,andnis the state dimension of system (1),equal to seven.

The solution of Eq.(14)is a random process closely related to the random variable Δ.Then,based on the PCE method,the state variable under the influence of Δ can be expanded,and the following formula is obtained.

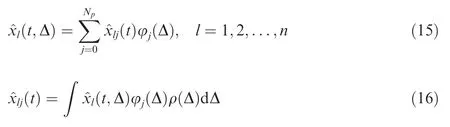
A week before Christmas, I asked myself, “What do I have that will make this Christmas special?” In all the houses that we had lived in before the divorce, I had always made time to be the interior decorator. I had learned how to wallpaper, to lay wooden and ceramic1 tile, to sew curtains out of sheets and even more. But in this rental2 house there was little time for decorating and a lot less money. Plus, I was angry about this ugly place, with its red and orange carpets and turquoise3 and green walls. I refused to put money into it. Inside me, an inner voice of hurt pride shouted, “We’re not going to be here that long!”

Considering that the random variable Δ obeys uniform distribution,Eq.(15) is substituted into Eq.(14),and its projection on the basis function is obtained via the Galerkin method,to generate the Deterministic Differential Equations(DDEs) corresponding to Eq.(14).This process can refer to our previous research work.37Due to the excessive relevant content and the space limitation of paper,the specific process is not carried out in detail.The equivalent DDEs obtained by PCE are as follows:

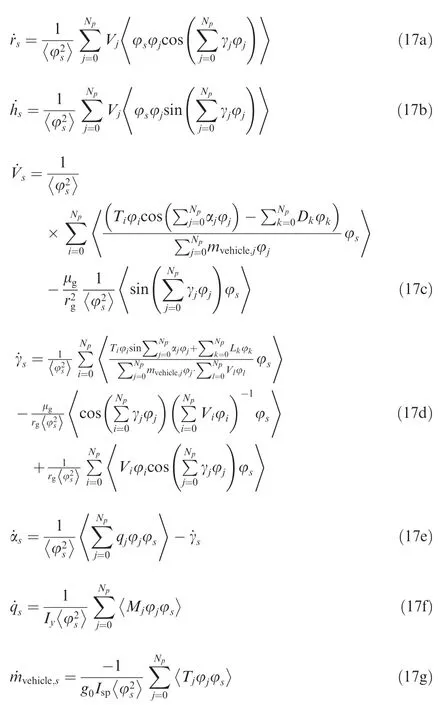
wheres=0,1,···,Np,and 〈·〉 is the mean operator.ri,hi,Vi,γi,αi,qi,mvehicle,i,i=0,1,···,Npare the polynomial chaos coefficients of stochastic state variablesr（Δ）,h（Δ）,V（Δ）,γ（Δ）,α（Δ）,q（Δ）,mvehicle（Δ）,respectively.Then,the stochastic dynamical system (14) in Rnis transformed into deterministic dynamical system in Rn（Np+1）.Therefore,the solutions of DDEs in Eq.(17) can be employed to characterize the flight states with uncertainties.

3.1.2.Correction of equivalent DDEs

Since the RDEs of ASVs are highly nonlinear,the long-term integration of polynomial (17) would cause the variation of random characteristics.38This will make the original basis family of random variables loses its representativeness,resulting in algorithm divergence.

To solve the divergence of PCE algorithm caused by the nonlinearity of ASVs,an adaptive polynomial chaos algorithm is proposed to update DDEs adaptively.In this algorithm,the Spectral Decomposition (SD) technology39is introduced to consider the change of the random characteristics of system state.Moreover,to perceive the significant changes of stochastic features (i.e.the original basis family is no longer applicable),the truncation error is used as an indicator40.The algorithm will adaptively updated the basis family,whenever the truncation error exceeds the threshold,to suppress divergence and improve the accuracy of PCE.The trigger conditions of updating the orthogonal basis are as follows40:

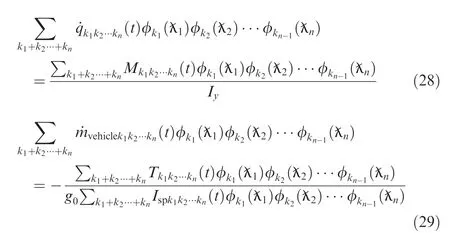
Then,then-fold integral and joint PDF in Eq.(30) can be transformed into

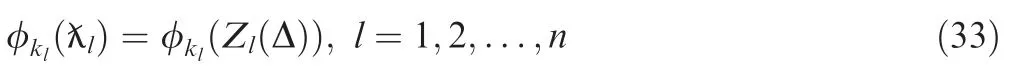
Consequently,Eq.(30)can be transformed into the following updated equivalent DDEs:

wherek1k2···kn=0,1,...,Np,l=1,2,...,n.

Furthermore,the variation of state space of stochastic system needs to be considered.Although the initial state is determined whent=t0,under the integral effect,the system state at the next moment is uncertain due to the uncertainty of state differential equations.Hence,the adaptive polynomial chaos algorithm also need to update the parameters of stochastic system state.The update criterion is42:

The expression of random field of update status can be written as follows:

thus,the initial state space of stochastic system at the next moment is updated.

Then,the new DDEs should be employed until a next time levelt2,at which criterion(18)is fulfilled again.Next,Eq.(20)is used to update the PDF of random variable,and apply the Schmidt orthogonalization rule to obtain the corresponding orthogonal basis.At the same time,judge whether Eq.(35)is true.If so,use Eq.(39) and Eq.(41) to update the initial state space of stochastic system.Finally,the updated DDEs are obtained by Eq.(34).The process should be repeated until the end of the integration.The adaptive polynomial chaos algorithm can be summarized as:

Under the condition of uncertain aerodynamic coefficient,the extended state constraints of(4c)and(11)determined by PCE are as follows:

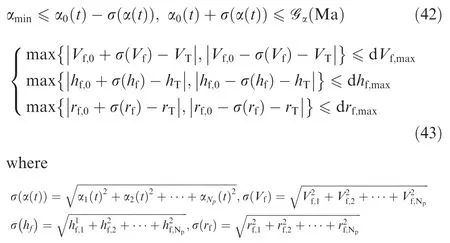
σ（·）represents standard deviation.αi,Vi,hi,andri(i=0,1,...,Np) are thei+1th PCE coefficients of angle of attack,velocity,height and horizontal displacement respectively,which are obtained by integrating the above DDEs.Ref.37 indicates that the first PCE coefficient of a random variable represents its average value.

3.2.Optimal control command design for uncertain system

For an uncertain system,in order to obtain the robust control command u*,the cost function of deterministic optimization problem must be modified.For uncertain system control optimization,the information (mean E（·）and variance σ2（·）) of stochastic state needs to be taken into account in the cost function.This information can be described by the state of augmented system,which is generated by the PCE method described in Section 3.1.

Then,the Augmented Optimal Control Problem (AOCP)considering system uncertainty can be described by the following equation

From Ref.14 and Ref.37,we can know that the average of uncertain parameter is the first value of its corresponding PCE coefficient,and its variance is the sum of squares of the corresponding PCE coefficients except for the first coefficient.Therefore,the mean and variance information of uncertain system can be expressed by Eqs.(45)–(46),and written into the cost function.

Then,the optimization problem(44)is solved to obtain the robust optimization control commands of uncertain system.The proposed Robust Control Command Optimization(RCCO) method can be summarized into the following steps,and the implementation process is shown in Fig.5.

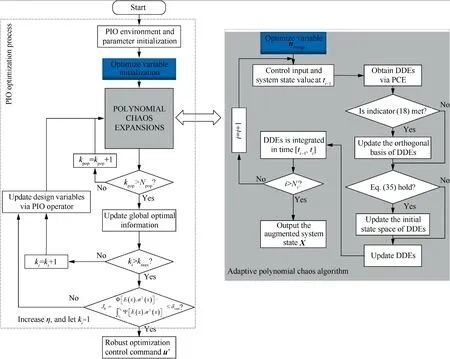
Fig.5 Robust control command optimization strategy based on polynomial chaos.

4.Analysis and application

In this section,first analyze the effectiveness of augmented system generated via the PCE method in predicting the evolution of uncertain systems.Then,a robust ascent trajectory of GHAME is designed by the RCCO method.Finally,the optimization results of the RCCO method and the deterministic optimization method PIO9are applied to the GHAME vehicle respectively,and the results are compared to verify the effectiveness of present algorithm.

4.1.Perturbation analysis of aerodynamic parameters

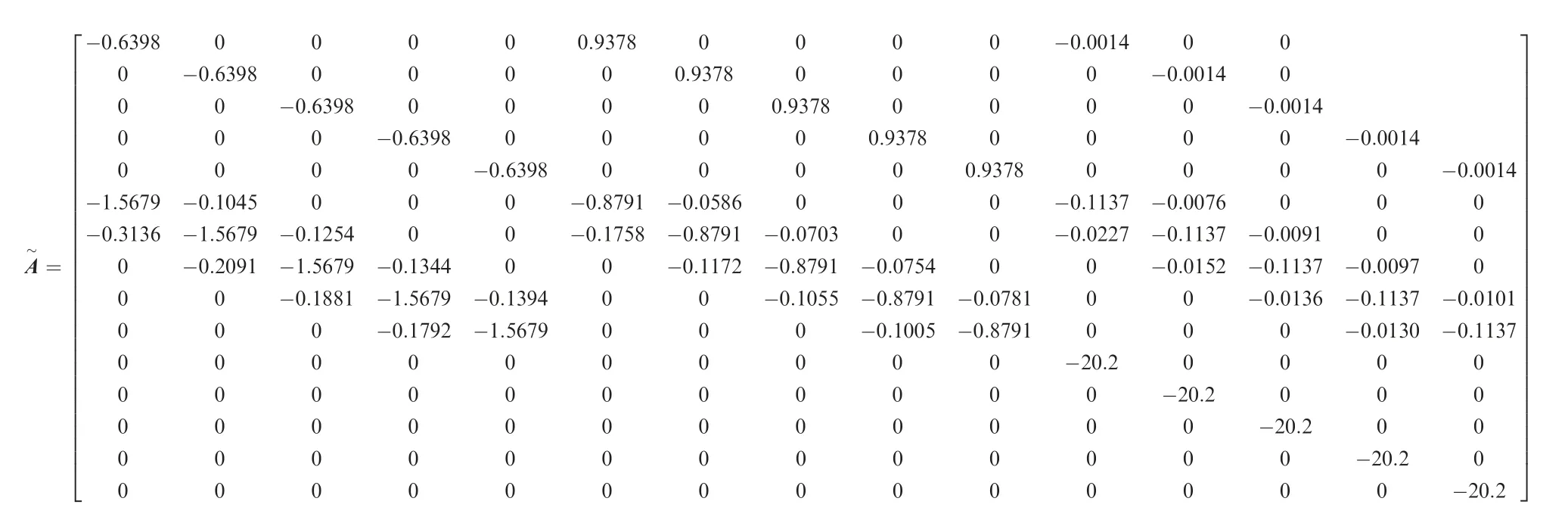
Taking the motion characteristics analysis of GHAME model33with parameter uncertainties as an example,the effectiveness of the above-mentioned method for describing the uncertain system is verified.The short-period approximate model of the GHAME vehicle in the trimming condition of 3Ma,15 km is taken as an example.For simplicity,it is assumed that the system parameters are dependent on a single random variable Δ.The short-period state vector is Xshort=[α,q,ηe]T,ηeis the measured elevator state.The control inputu=δeis the elevator command(the unit is degree).The matrix values in the vehicle model are as follows:

Assume that the probability distribution of random variable Δ is the uniform distribution,and Δ ∈[- 0.2,0.2].Set the highest order of orthogonal basisp=4,and the necessary parameters for the criteria are ν1=ν2=ν3=2/3,χ=0.5,and ϑ1=10-2,respectively.The augmented matrix after uncertainty quantification is represented byas shown below:

Figs.6-7 show the prediction ability of augmented system to the dynamic characteristics of uncertain system (47).In Fig.6,the circles represent the eigenvalues of augmented system,and * represents the eigenvalues of uncertain system obtained by MC simulation.Fig.7 shows the pitch rate response of the system with 20% uncertainty in the aforementioned parameters.The predicted trajectory bounds obtained by PCE,and pitch rate curves given via MC are represented by dashed-lines and dark-solid lines,respectively.

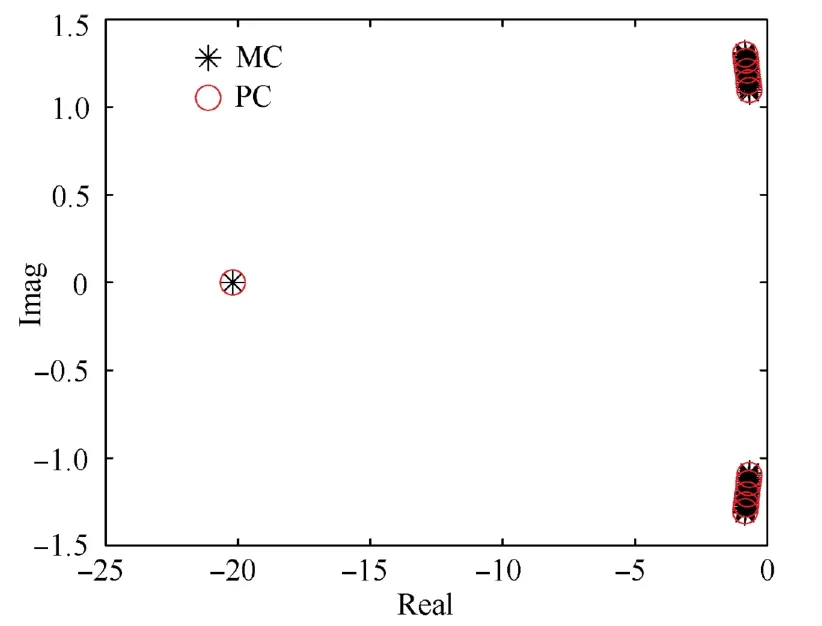
Fig.6 Closed loop eigenvalue distributions for a short-period mode for ±20% parameter uncertainty.

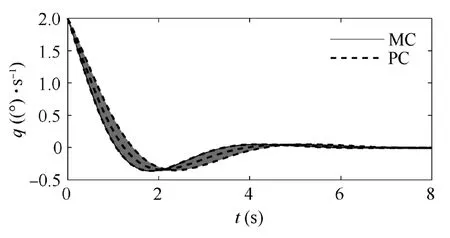
Fig.7 PC and MC system response to ±20% parameter uncertainty.

According to Fig.6,the augmented system can capture the eigenvalue distribution of uncertain system.In addition,it can be seen from Fig.7 that the bounds predicted by the augmented system are in excellent agreement with the pitch rate curves obtained by the MC method.The simulation results show that the augmented system generated by the improved PCE algorithm can be applied to predict the kinematic characteristics of uncertain system and analyze its stability,which has higher computational efficiency than the MC method.

4.2.Robust optimization design of control command

4.2.1.Simulation conditions

In this section,the proposed method is applied to the GHAME vehicle,and the effectiveness of method is verified by simulation.Set the initial state as:Ma（t0）=5,h（t0）=20.4 km,r（t0）=0 km, α（t0）=2o,γ（t0）=10o,mvehicle（t0）=116077 kg;The ascent target point is:MaT=10,hT=34.6 km,rT=79.7 km.Define the aerodynamic force Coefficient of Coincidence (COC)KAto describe the aerodynamic perturbation during the ascent,the lift and drag can be expressed as:

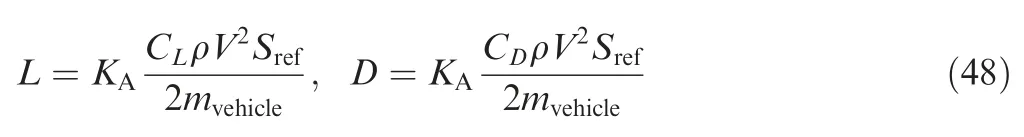
TheKA=1 means that the actual aerodynamic force is consistent with the nominal aerodynamic force.In actual flight,due to the influence of air density,atmospheric temperature,and airplane structural factors,the COC often varies within a certain range.Therefore,the case of 20%aerodynamic force perturbation is considered,i.e.,assumes thatKA∈[0.8,1.2] and satisfies a uniform distribution.

Compared with the complex constraints faced by ASVs,the simplified version of (4) is considered in the simulation,as shown below:

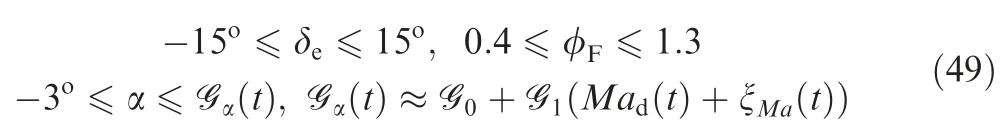
where G0=-8,G1=2.43Madis the desired Mach number,ξMais the speed deviation,Mad≫|ξMa|.According to the aerodynamic database of GHAME,33the minimum negative angle of attack is -3o,that is,the lower bound of the angle of attack of the GHAME vehicle is -3o.Then,the final constraint range of AOA is the red shaded part in Fig.8.

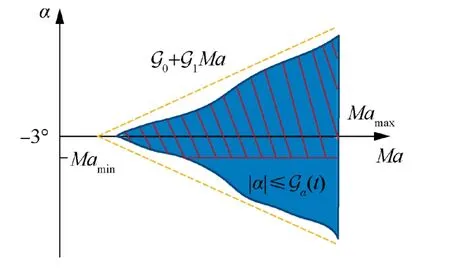
Fig.8 Angle of attack constraint.

4.2.2.Robust optimization of ascent trajectory

The RCCO method not only considers the system uncertainty in the solution process,but also improves the traditional optimization problem by taking SDF as one of the performance indexes.To verify the effectiveness of proposed method,the ascent trajectory will be designed based on the RCCO method and the traditional optimization method,respectively.

For traditional trajectory optimization,which is designed only for standard systems without the uncertainty,as shown in Eq.(50).The objective function is to minimize fuel consumption and reach the target point.Next,a PIO algorithm in Ref.9 is used to solve the optimization problem (50).

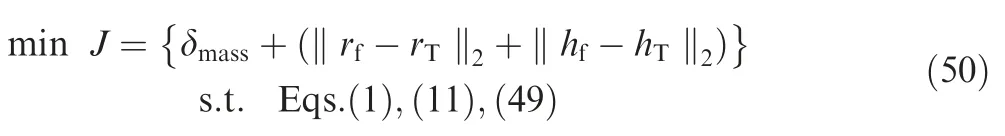
The RCCO method takes into account the uncertainties in the trajectory optimization problem and the solution process.In addition,the SDF of GAHME along the trajectory is considered in the optimization objective function,then the optimization problem (50) is converted to (51).

Finally,the optimization problems(50)and(51)are solved by PIO method and RCCO method respectively,and the generated optimization control instructions are shown in Fig.9.In the figure,the black-solid represents the optimal control variable udobtained by PIO solving problem (50),and the redsolid represents the optimal control variable uRgiven via the RCCO method solving problem (51).

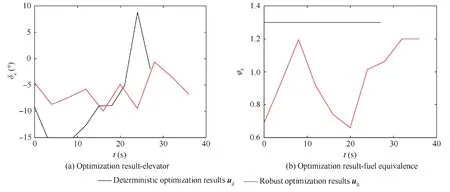
Fig.9 Optimal control variables obtained by RCCO method and deterministic trajectory optimization method.

Firstly,the effectiveness of the above two methods for solving optimization problems (50) and (51) is analyzed.The resulted optimization variable udis substituted into the deterministic system (1),and uRis applied into the DDEs constructed in Section 3.1,and the corresponding state variables xdetand XDDEsare obtained by integration respectively.In Fig.10,black-solid lines are the corresponding state curves xdet(deterministic system).The red-solid lines are the E（XDDEs）curves,which represent the mean values of state variables of the stochastic system(14).The expression of E（XDDEs）is Eq.(45).Among them,Fig.10(e) shows the variation curve of AOA with the Mach number,and the upper and lower boundaries of its constraint at different flight speeds.

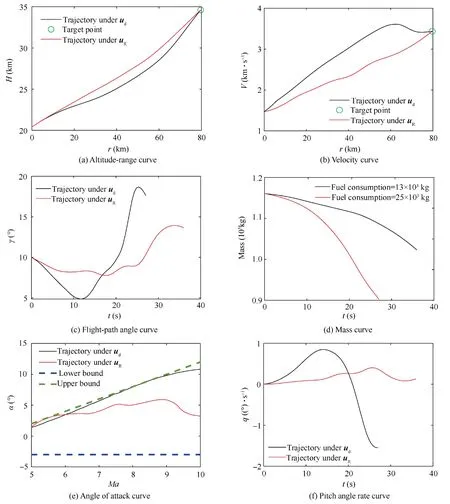
Fig.10 State variable curves of two systems.

According to Fig.10,the optimization problems (50) and(51) have obtained solutions satisfying state constraints under the corresponding algorithms.In addition,compared with the PIO method,the optimized trajectory via the RCCO method is more gentle.That is,the amplitude and variation rate of state(such as AOA α and fight-path angle γ) and the amplitude of control variables (δeand φF) are smaller.Of course,this also leads to the trajectory optimized by the RCCO method has longer climbing time and greater fuel consumption.

Then,in order to verify the robustness of the optimal control commands obtained by the RCCO method,the udand uRare substituted into the stochastic system (14) for MC simulation.Consider that the aerodynamic parameters of GHAME satisfy Eq.(48),udand uRare respectively applied to this stochastic system for 500 MC simulations.Fig.11 and Fig.12 show the MC simulation results of the height-range curve and the velocity-range curve.

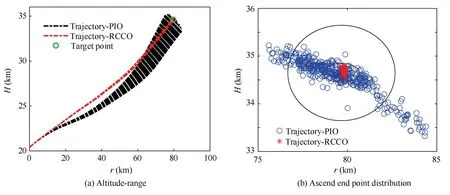
Fig.11 MC simulation results of altitude-range with aerodynamic parameter uncertainty.

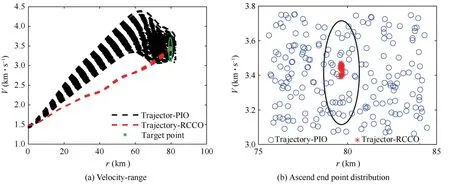
Fig.12 MC simulation results of velocity-range with aerodynamic parameter uncertainty.

The two ellipses in Fig.11(b) represent the boundaries corresponding to single and triple of the allowable maximum errors between the terminal position and target position (dhf,max=300 m,drf,max=1000 m),respectively.The short-axis and long-axis of the first ellipse in Fig.11(b) represent the distance of 300 m and 1000 m from the height and horizontal displacement of the target point,respectively.And the short-axis and long-axis of the second ellipse are 1000 m and 3000 m.It can be clearly seen from Fig.11 that the trajectories generated by executing 500 MC under uRsatisfy the set terminal position constraint conditions,and their distribution is relatively concentrated.This indicates that the optimized trajectory given via the RCCO method has strong robustness and terminal position constraint satisfaction ability.

The ellipses in Fig.12 represent the same implication,which represent the boundary formed by the set terminal velocity and horizontal displacement constraints (dVf,max=300 m/s,drf,max=1000 m).If the terminal state of trajectory is outside the ellipse,it means that the resulted trajectory does not meet the set terminal constraint.The short and long axes of the ellipse in Fig.12 are 300 m/s and 1000 m,respectively.According to Fig.12(a),we can conclude that under the reference control command obtained by the proposed method,the flight speed of GHAME is little affected by the uncertain parameters.According to Fig.12(b),it can be seen that under uR,the variation range of terminal velocity is within the constraint range of the optimization problem (51).However,in the uncertain system,the deterministic optimization results udcannot ensure the dispersion degree of terminal velocity and position.

Next,the ability of the RCCO method to satisfy the system state constraints under parameter uncertainties is verified.Although the AOA shown in Fig.10 satisfies the constraint(49),it is impossible to prove whether AOA can still meet this constraint within the variation range of all uncertain parameters.Fig.13 demonstrates these curves of AOA obtained by 500 MC simulations and the constraint of AOA in the ascent phase.

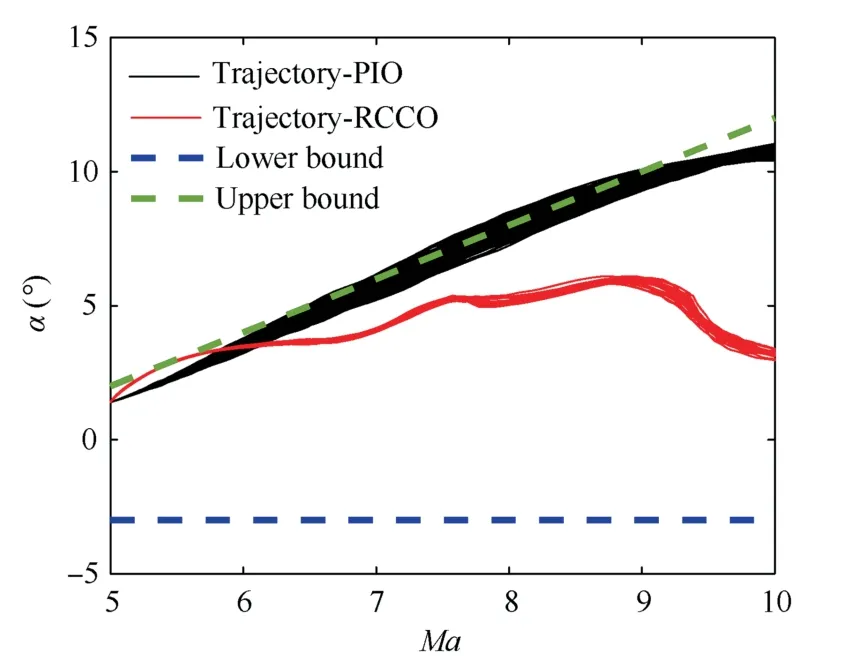
Fig.13 MC simulation results of AOA and its constraints.

Fig.13 exhibits that under the uncertain aerodynamic parameters,the reference control commands obtained by the RCCO method can ensure the vehicle still satisfies the constraint of AOA.

According to the above simulation analysis,under the condition of parameter perturbation,the optimization results generated by the traditional deterministic optimization method are larger affected by uncertainty,and would have a large deviation from the nominal trajectory.Thus,it is difficult to adapt to the actual flight environment.In the RCCO method,the influence of uncertainty on the optimization results is fully considered,so the optimization results have excellent robust stability.Moreover,the design variable of RCCO method is the actual control inputs,which can ensure the feasibility of designed trajectory and reduce the burden of control system in dealing with uncertainties.

Finally,the SDF characteristics of GHAME under the ascent trajectory obtained via the RCCO method are evaluated to verify whether the method can optimize the SDF characteristics while ensuring robustness.Fig.14 describes the shortperiod flight quality ξsp-/（nz/α）of GHAME under the ascent trajectories shown in Fig.11,wherenzrepresents the normal overload.In the figure,the green curve is the SDF characteristic trend of GHAME under the trajectory given via the RCCO method,and the orange curve represents the SDF characteristic trend under the trajectory provided by the PIO method.

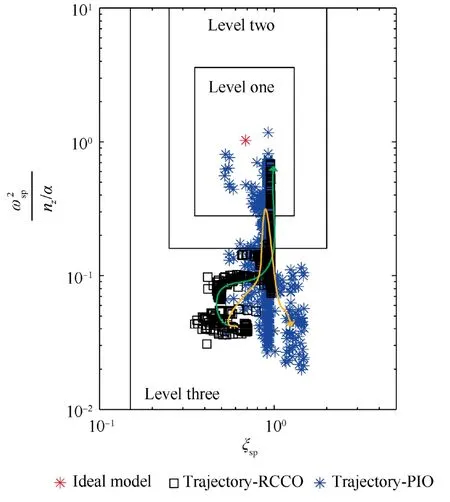
Fig.14 Flying quality evaluation curve under different ascent trajectories.

According to the evaluation results of SDF under different ascent trajectories shown in Fig.14,along the ascent trajectory obtained by the RCCO method,the SDF characteristics level of GHAME is gradually approaching Level-One.However,under the trajectory generated by solving the optimization problem (50),although the SDF characteristic level has an improvement trend,it finally drops back to Level-Three.It can be concluded that the RCCO method can obtain an ascent trajectory with better flight quality and robustness than the traditional optimization method.Thereby,a good front-end input could be provided to the controller to balance the burden of trajectory planning and control system design.

Based on the above simulation results,it can be seen that the resulted trajectory of the RCCO method is low sensitivity to uncertainty,and the RCCO method can optimize the SDF characteristic while ensuring robustness.However,it consumes 12×103kg more fuel than the conventional optimization method.This is also at the expense of fuel consumption to obtain an ascent trajectory with better robustness and control performance.

5.Conclusions

This paper proposes a multi-constraint robust trajectory optimization method.The robust optimization method combines the characteristics of ASVs,improves the traditional deterministic trajectory optimization problem,and takes some control performance as one of the optimization objectives.In addition,this method considers the influence of parameter uncertainty in trajectory optimization.Meanwhile,the actuator saturation constraint,FER constraint,and engine un-start constraint are considered.The proposed method is applied to optimize the ascent trajectory of GHAME with parameter uncertainty to reduce the influence of parameter uncertainty on the designed trajectory.

This robust optimization method takes the actual control input (elevator and FER) as the design variable,which not only ensures that the optimized trajectory is actually controllable,but also enables the SDF characteristic to be considered in the optimization objective.Thus,a reference control command with strong robustness and good SDF characteristic is provided,which reduces the burden of control system.The MC simulation results show that,compared with the traditional deterministic optimization method,the results obtained by the proposed optimization method have better robustness,SDF characteristic,and the ability to satisfy constraints.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgements

We thank the anonymous reviewers for their critical and constructive review of the manuscript.This study was co-supported by the Fundamental Research Funds for the Central Universities,China (No.NS2021061),the Six Talent Peaks Project in Jiangsu Province,China (No.KTHY-025),the China Postdoctoral Science Foundation No.2020M681586),the Natural Science Foundation of Jiangsu Province (No.BK20200437),the Interdisciplinary Innovation Foundation for doctoral students of Nanjing University of Aeronautics and Astronautics (No.KXKCXJJ202008).