Neural network-based model predictive control with fuzzy-SQP optimization for direct thrust control of turbofan engine

Yangjing WANG,Jinquan HUANG,Wenxiang ZHOU,Feng LU,Wenhao XU

Jiangsu Province Key Laboratory of Aerospace Power System,College of Energy and Power Engineering,Nanjing University of Aeronautics and Astronautics,Nanjing 210016,China

KEYWORDS Direct thrust control;Fuzzy-SQP algorithm;Limit protection;Neural network;Nonlinear model predictive control;Random forest;Turbofan engine

Abstract A nonlinear model predictive control method based on fuzzy-Sequential Quadratic Programming (SQP) for direct thrust control is proposed in this paper for the sake of improving the accuracy of thrust control.The designed control system includes four parts,namely a predictive model,rolling optimization,online correction,and feedback correction.Considering the strong nonlinearity of engine,a predictive model is established by Back Propagation(BP) neural network for the entire flight envelope,whose input and output are determined with random forest algorithm and actual situation analysis.Rolling optimization typically uses SQP as the optimization algorithm,but SQP algorithm is easy to trap into local optimization.Therefore,the fuzzy-SQP algorithm is proposed to prevent this disadvantage using fuzzy algorithm to determine the initial value of SQP.In addition to the traditional three parts of model predictive control,an online correction module is added to improve the predictive accuracy of the predictive model in the predictive time domain.Simulation results show that the BP predictive model can reach a certain degree of predictive accuracy,and the proposed control system can achieve good tracking performance with the limited parameters within the safe range.

1.Introduction

The primary mission of aeroengine is to provide proper thrust for the aircraft in safe conditions.1,2However,thrust and some parameters that characterize the safety performance of the engine are not measurable.The traditional strategy of engine control is to control thrust indirectly with some measurable parameters by the relationship between thrust and the measurable parameters.3,4However,the relationship between the two may change with engine degradation,maintenance,etc.,causing control errors to increase over time.5Therefore,direct thrust control is particularly proposed.In addition,since some performance parameters such as surge margin are unmeasurable,a large margin is reserved even in the worst conditions to ensure the safe and stable operation of the engine,so the engine performance cannot be fully utilized.6,7In addition,the engine needs to meet various restrictions during operation,such as no over-rotation,no over-temperature,no surging,and so on.4Limit protection is also an important part of the engine control system.Compared with traditional control methods,MPC (Model Predictive Control) can not only deal with the system’s time delay and limit management,but also achieve optimal control based on the predictive model,so that the control system can achieve good control performance to meet control requirements.8–11

Vroemen et al.12successfully applied MPC based on successive linearization model to laboratory gas turbine installations.Du et al.13proposed an adaptive model predictive controller for turbofan engines to realize the steady-state control and transition-state control of the engine within the entire flight envelope.But the flight envelope needs to be divided to establish several linear predictive models.Brunell et al.14applied constrained NMPC (Nonlinear Model Predictive Control) to the engine based on a SRTM (Simplified Real Time Model),which only contains few states.DeCastro15designed a model predictive controller which crucial component is a rate-based linear parameter-varying model.Richter et al.16realized simplified calculation of the optimization in NMPC using state variable model.Wang et al.17so adopted state variable model to design a nonlinear model predictive controller to investigate the process of rotor speed variation under tiltrotor cruise state.Most of the above-mentioned are based on piecewise linear models for model predictive control.Obviously,this method has well real-time performance,18–21however,the accuracy of the model cannot be guaranteed.So,in response to this disadvantage,Zheng et al.22proposed a nonlinear model predictive controller scheme based on MRR-LSSVR (Multi-input multioutput Recursive Reduced Least Square Support Vector Regression)predictive model to obtain better engine response.Unfortunately,the real time performance of SVR (Support Vector Regression) will be decrease rapidly as training data increases,several sub predictive models are established for the entire flight envelope so that data storage increases.23,24Therefore,a BP neural network based predictive model is proposed.The neural network has the ability of approximating nonlinear function and has good real-time performance.25The neural network-based predictive model can be trained offline,which can reduce the online computational burden of the entire control system.

SQP is a very effective algorithm for nonlinear constrained optimization problems of nonlinear model predictive control.11Based on an initial value,iterative algorithm is used to find the optimal solution.But this algorithm has the disadvantage of falling into the local optimization easily.Therefore,the fuzzy-SQP algorithm is proposed in this paper to avoid falling into local optimization.Zadeh proposed the concept of fuzzy set in 1965.Mamdani26used fuzzy logic for steam engine control.Since then,fuzzy control has been widely and fruitfully applied in industrial process control,robotics,and transportation.27,28In this paper,the fuzzy algorithm and the SQP algorithm are combined,the fuzzy algorithm is adopted to determine the initial value of SQP algorithm to avoid falling into local optimization.

The major contribution of this paper is to design a nonlinear model predictive controller for direct thrust control of turbofan engine.This system meets the requirements of tracking performance and limit protection simultaneously.The predictive model is based on BP neural network,which structure is determined by random forest and the analysis of actual situations.Meanwhile,fuzzy-SQP algorithm is proposed to be the algorithm of nonlinear constrained optimization problems to avoid trapping into the local optimization.In addition,online correction module is added to improve the accuracy of predictive parameters.For purpose of verifying the effectiveness of the designed controller,a series of simulations are carried out for different operating points.Simulations show that the predictive model based on BP neural network can achieve a certain accuracy of the predictive parameters,and the designed controller has good tracking performance with the limited parameters within the safe range.

The remainder of the paper is organized as follows.Section 2 briefly describes the control scheme and explains the role of each part.Section 3 processes data and establishes a neural network model;Section 4 briefly describes the principle of the fuzzy-SQP algorithm,and a nonlinear model predictive controller is also designed in this section;Section 5 gives simulation results and analysis;The conclusions are summarized in Section 6.

2.Scheme of control system

The purpose of the proposed system is to track the thrust command with the limited parameters within the safe range.As shown in Fig.1,the structure of the control system main includes thrust estimator,neural network predictive model,online correction,feedback correction and rolling optimization.The thrust estimator can accurately estimate thrust with engine degradation,maintenance,etc.,which is not described in detail in this article.29The BP neural network predictive model is adopted to predict the parameters in the predictive time domain.The input of the predictive model main contains two parts: sequence of control variables which are obtained from rolling optimization module and measurable parameters which are corrected by online correction module.The output of the predictive model also contains two parts: measurable parameters and unmeasurable parameters such as thrust.During the process of prediction,online correction module is used to correct measurable parameters based on the error between predictive model and the engine to improve the accuracy of prediction of the thrust.Feedback correction is to correct predictive thrust according to the error between predictive model and the thrust estimator.Then the optimization objective function can be calculated and solve the optimization problem by fuzzy-SQP algorithm to obtain the control variables in rolling optimization module.

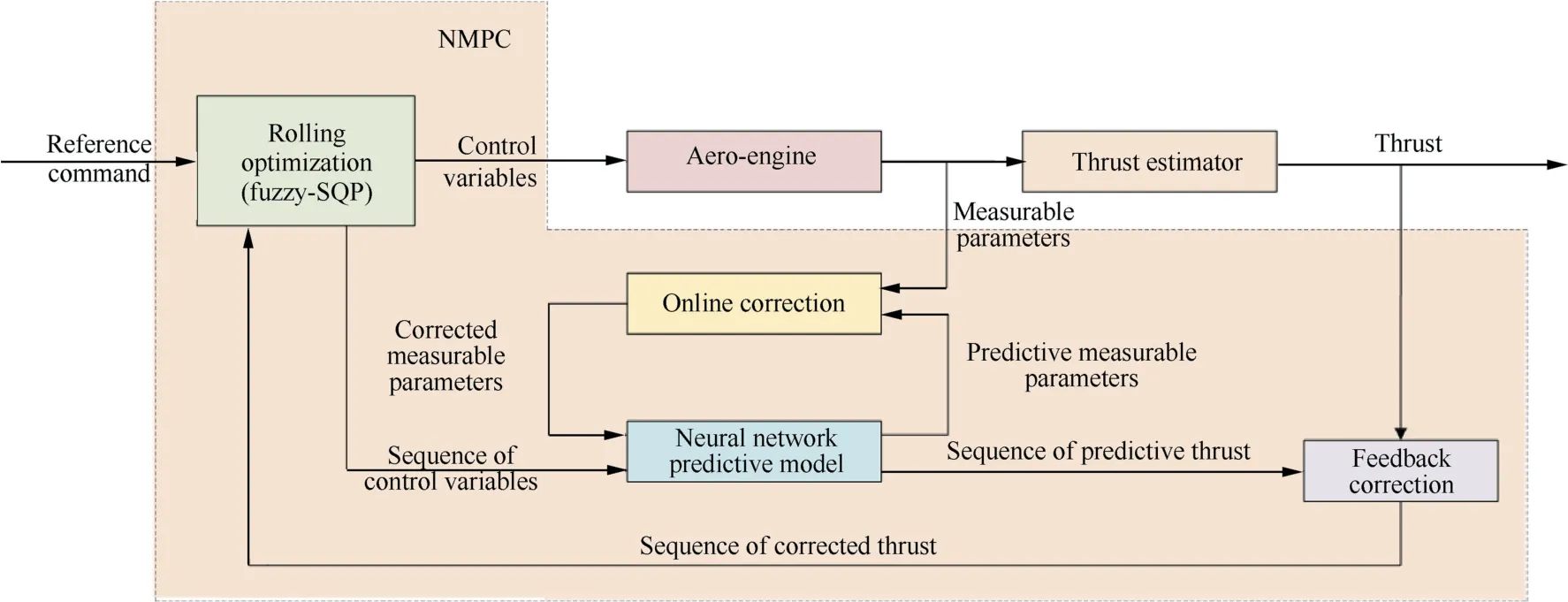
Fig.1 Schematic of NMPC.

3.Neural network predictive model

3.1.BP neural network

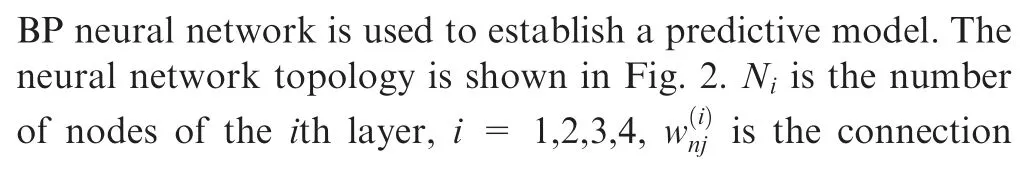
Fig.2 BP neural network topology.

The specific training process is as follows.SupposeStraining samples are used to train the network,one of which is samples.For samples,the input of thenth neuron of theith layer is

The output of thenth neuron of theith layer is

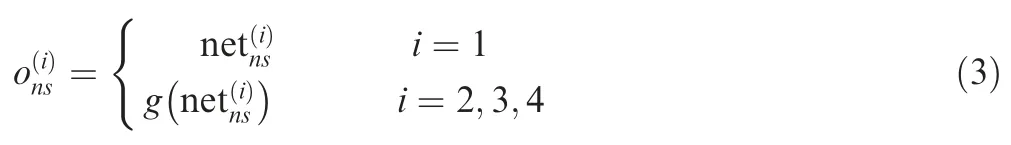
whereg（·）is the activation function.

The quadratic error function forStraining samples is

If the learning process adjusts the weighting coefficient in the direction whereLdecreases the fastest,then the weighting coefficient increment formula of any neuronnin theith layer is

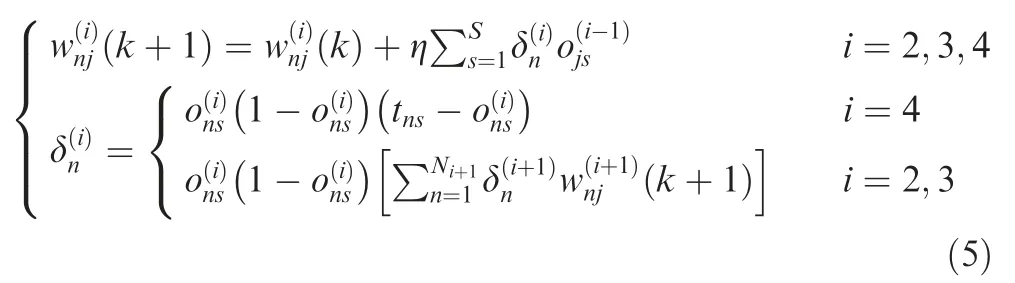
where η is the learning efficiency,η>0.

The steps of the BP learning algorithm are

Step 1.Initialize each weighting coefficient,and calculate the output of each neuron according to Eq.(2) to Eq.(3).

Step 2.Calculate the quadratic error function according to Eq.(4).

Step 3.adjusting the weighting coefficient according to Eq.(5).

Step 4.Return to Step 2 to recalculate the output and error until the error meets the requirements.

3.2.Parameters selection with random forest algorithm

After determining the structure of BP neural network,the input parameters and the output parameters should be determined.To simplify the structure of the neural network and improve the accuracy of prediction,random forest algorithm is used to determine the input variables of the neural network.

Random forest is a machine learning algorithm proposed by Breiman in 2001.30Random selection is used in feature selection,and the integrated decision tree method of bagging technology is used in the number of samples.Genuer et al.31discussed the feature selection method based on random forest in detail in the article.Ndecision trees is generated by the method of bootstrapping to form a random forest.For each decision tree,about one-third of the training set will not be sampled using bootstrapping,these data are called Out of Bag (OOB) data.OOB data can be used to estimate the error of the result of each decision tree(eOOB1).After randomly adding noise interference to OOB data,the error can be calculated again which is calledeOOB2.Then the Variable Importance(VI)which is used as a measure of the importance of the variable can be calculated as follows.

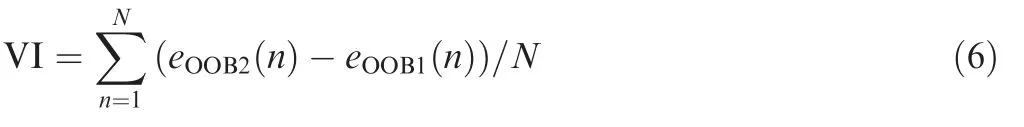
IfeOOB2rises after adding random noise,it indicates that this variable has a great influence on the result,and thus the importance is relatively high.The steps of variable selection are as follows.

Step 1.Sort the characteristic variables by random forest in descending order of VI according to Eq.(6).

Step 2.Remove the unimportant variables from the current variables if the order of magnitude of VI is less than 10-5,thereby obtaining a new variable set.

Step 3.Use the new variable set to establish a new random forest and calculate the VI of each variable in the variable set and sort it according to Eq.(6).

The parameters that can be measured by sensors to train neural network are shown in Table 1.Because the engine can usually be regarded as a second-order system,so the lag time is two moments.Thekin Table 1 represents the current moment.

Follow the steps described before to select the important variable for thrust using random forest algorithm,and the finally selected variables and their VI are shown in Table 2.

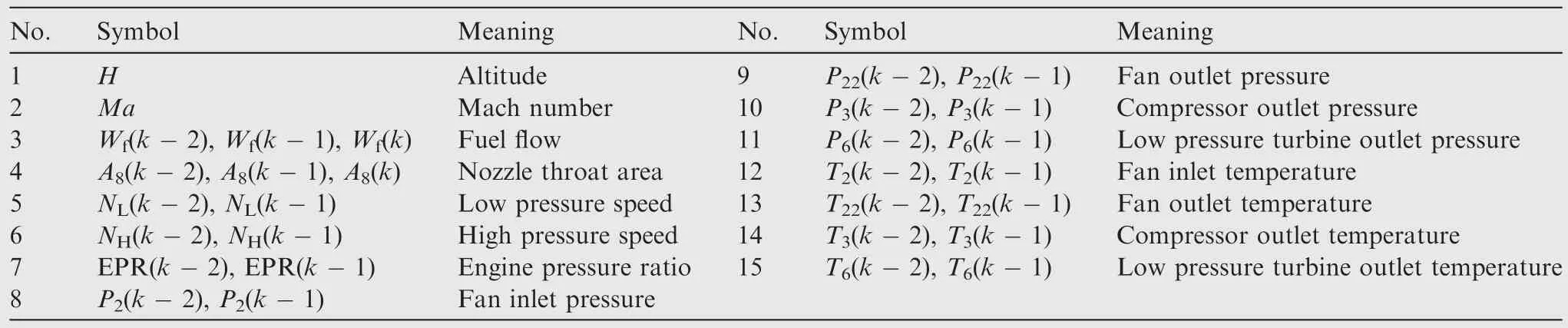
Table 1 Unfiltered variables.

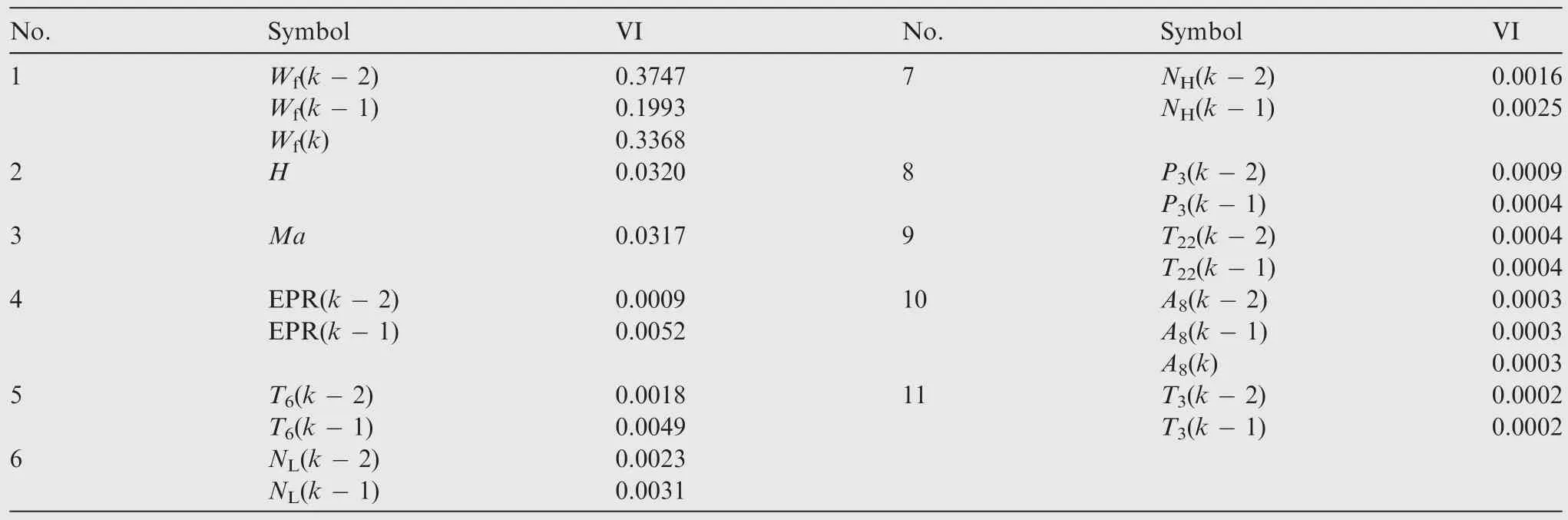
Table 2 VI of the final selected variables.

After determining the input of the neural network,the output parameters are selected as follows.First,the variable of thrustFas the control target should be selected.Then,the limited parameters which need to be in the safe range should also be included such as surge margin of compressor SMc.The parameters whose past moments also serve as the input of the neural network needs to be selected to reflect the dynamic characteristics of the engine.

3.3.Training and testing of neural network predictive model

From the previous part,it is determined that the input of the neural network predictive model areH(k),Ma(k),Wf(k-2),Wf(k-1),Wf(k),A8(k-2),A8(k-1),A8(k),NL(k-2),NL(k-1),NH(k-2),NH(k-1),EPR(k-2),EPR(k-1),P3(k-2),P3(k-1),T22(k-2),T22(k-1),T3(k-2),T3(k-1),T6(k-2),T6(k-1),and the output areNL(k),NH(k),EPR(k),P3(k),T22(k),T3(k),T6(k),SMc(k),F(k).The structure of neural network is BP neural network with two hidden layers,and the number of hidden layer nodes are 50 and 30 respectively.

The performance of the neural network relies on the quality of the training sample.A training sample is a pair of input dataand output data.To ensure that the trained neural network has better performance,the sample data used for training in this paper not only cover all relevant stable operation point,but also cover all dynamic processes.

According to the different state points in the flight envelope,the corresponding measurable parameters and performance parameters can be obtained based on the CLM(Component-Level Model).And the state points are selected according to the following rules: the altitudeHchanges from 0 to 20 km with an increment of 1 km,and the Mach numberMachanges from 0 to 2 with an increment of 0.2.Changing the fuel flow and nozzle throat area at each operating point makes the high-pressure corrected speed change from about 67.5% to about 100%,and more than 70000 sets of training data are obtained.For sake of enhancing the predictive accuracy of the neural network,the data needs to be normalized before training.

After the neural network is trained,some simulations are carried out to verify the accuracy of the neural network.Under the working environment ofH=0 km andMa=0,the control variables are changed and applied to the engine and the neural network model respectively,and the simulation results and errors of each output parameters are shown in Fig.3 and Fig.4 (all parameters in the figures in this article are relative values of design points).The error calculation formula is:

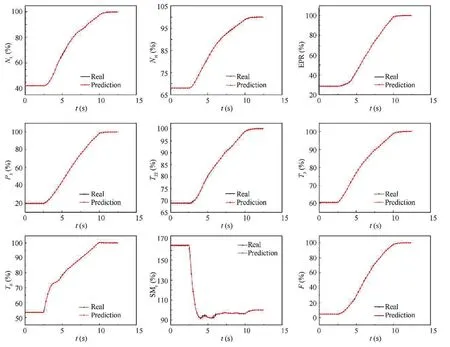
Fig.3 Test results of neural network predictive model at H=0 km and Ma=0.

where y（t）is the response of the engine,andis the response of the neural network model.

From the above simulation results,the established predictive model can reflect the engine output response.Fig.4 shows that the response error of most of the parameters is close to 0,in addition to that the error of SMcwill be large during the transient process which is about 2%.The following is to verify the predictive accuracy of the predictive model at the different operation point with different input.The simulations are shown in Fig.5 and Fig.6.Taking the thrust as an example,the neural network predictive model can accurately reflect the engine response in different situations,and the predictive error of most parameters is close to 0,in addition to that the error of SMcis a little bit larger which is less than 2%.

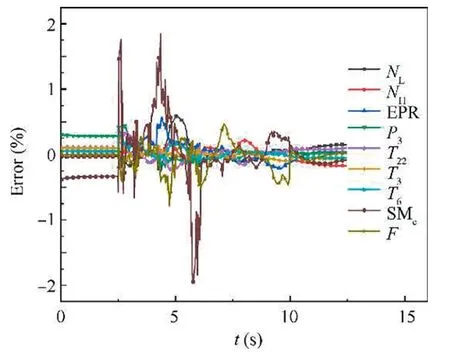
Fig.4 Response error of engine and predictive model.

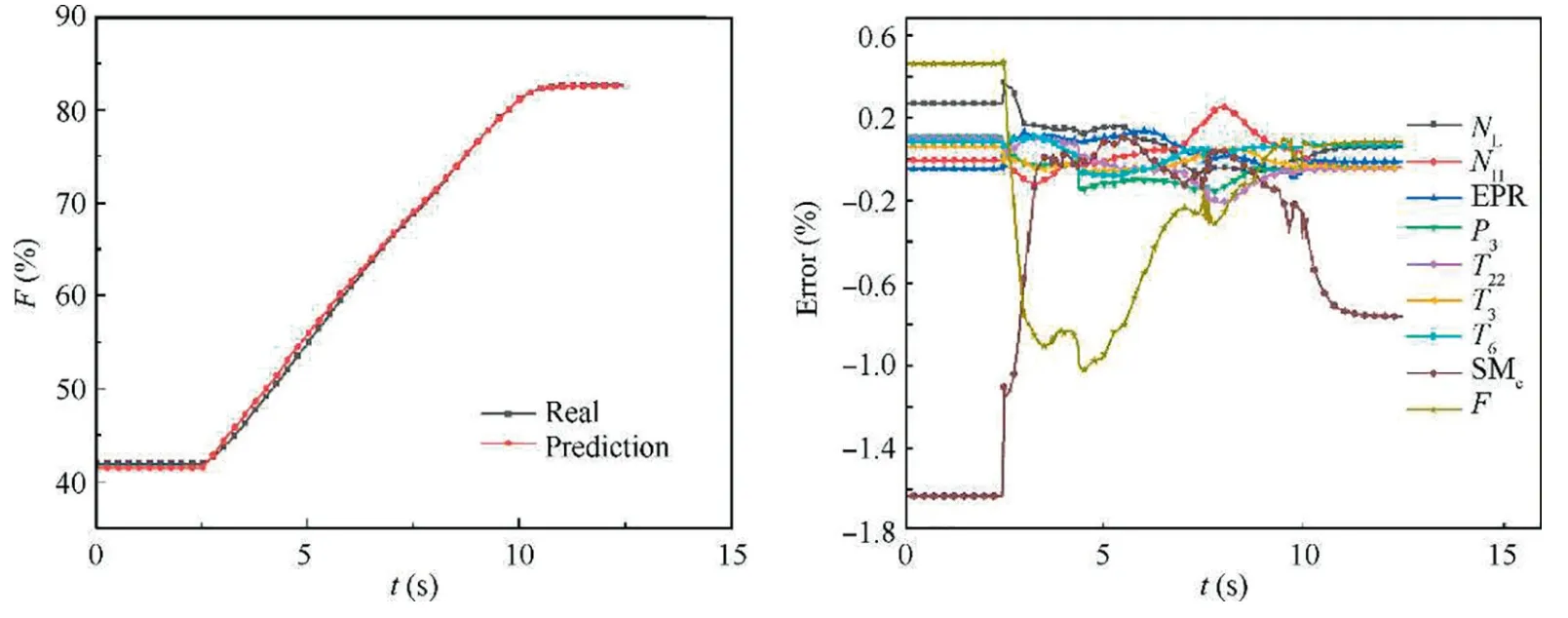
Fig.5 Test results of neural network predictive model of H=0 km and Ma=0 with different inputs.

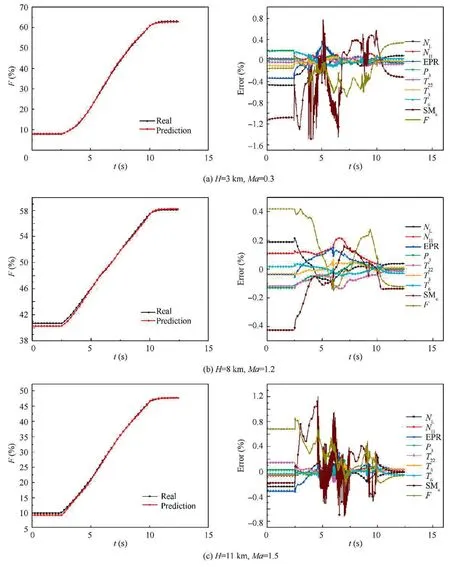
Fig.6 Test results of neural network predictive model.

4.Fuzzy-SQP based NMPC control system

4.1.Optimization algorithm

The principle of NMPC is shown in Fig.7.The NMPC is a closed loop,constrained online optimization control algorithm.^Fis the predictive thrust.

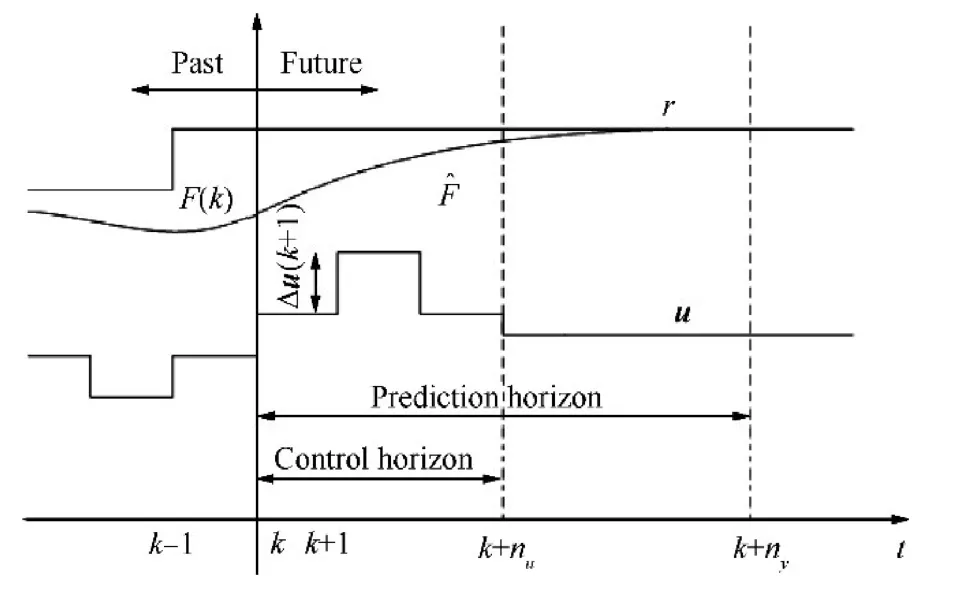
Fig.7 Principle of NMPC.

Define the predictive control error as

wherer（k）is the reference command,andis the corrected predictive output.

Define the control increment as

where u（k）is the control variable at the current moment,u（k-1）is the control variable at the previous moment.

At each momentk,the optimization to be solved is

where ΔF is ΔF（k+i）of each moment of the prediction horizonny,Δu is the Δu（k+i）of each moment of the control horizonnu,i=0,1,...,ny-1,andny≥nu.Ifnu＜i＜ny,then Δu（k+i）=0.Q and R are positive definite and symmetric matrix.

To make sure the safe and stable operation of engine,some limits such as surge margin should be taken into account in NMPC,which are as follows.

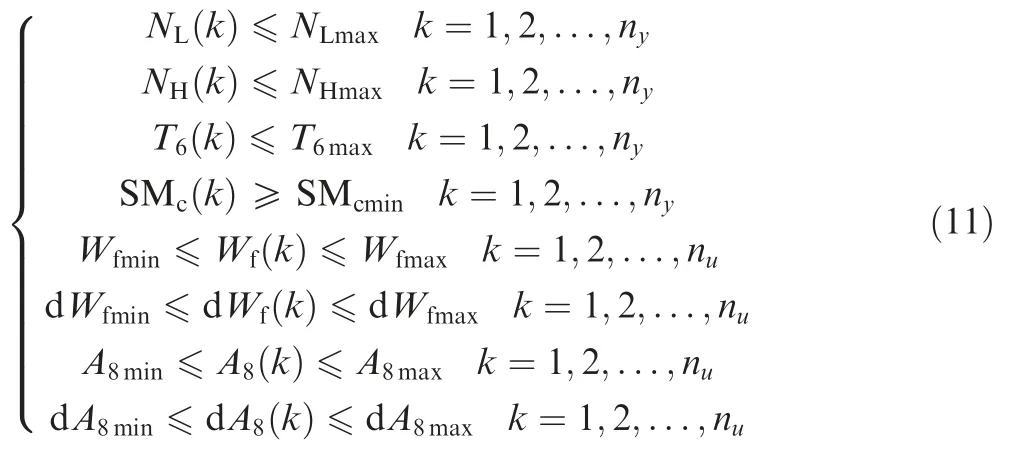
SQP is a widely used algorithm for nonlinear constrained optimization problems of nonlinear model predictive control.SQP transforms the original problem into a series of quadratic programming sub-problems to be solved to obtain the optimal solution of the original problem.However,SQP whose solution is based on an initial value has the disadvantage of falling into the local optimization easily.Therefore,fuzzy-SQP is proposed to avoid this disadvantage by using fuzzy algorithm to determine the initial value of SQP.

The fuzzy system includes four modules:fuzzification,fuzzy inference,clarification,and knowledge base.The input of the fuzzy system is determined as the error of thrusteFrbetween referencerand responseFand the derivative of the error deFr.Δu=[ΔWf,ΔA8]Twhich includes the increase of fuel flow ΔWfand the increase of nozzle throat area ΔA8is selected as the output of the fuzzy system.Fuzzy the input and output variables into the following categories: ‘‘NB (Negative Big)”,‘‘NM (Negative Medium)”,‘‘NS (Negative Small)”,‘‘ZO(Zero)”,‘‘PS (Positive Small)”,‘‘PM (Positive Medium)”,and ‘‘PB (Positive Big)”.The fuzzification of the input and output are shown in Fig.8,Fig.9,respectively.

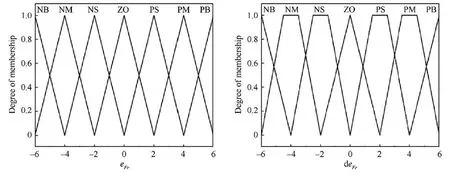
Fig.8 Fuzzification of input.

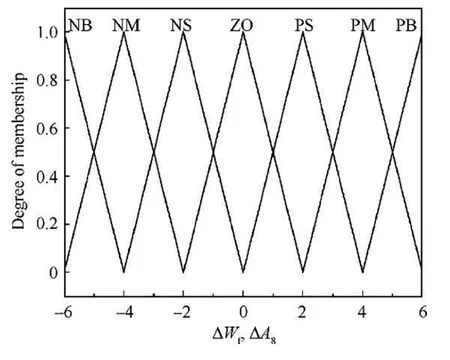
Fig.9 Fuzzification of output.

According to the principle of the engine and control law,the following control rules of fuel flow and nozzle area are summarized,as shown in Table 3.

What Table 3 shows are actually a set of control rules,taking ΔWfas an example,fuzzy conditional sentences expressed in the form of ‘‘IF···THEN···”,such as:

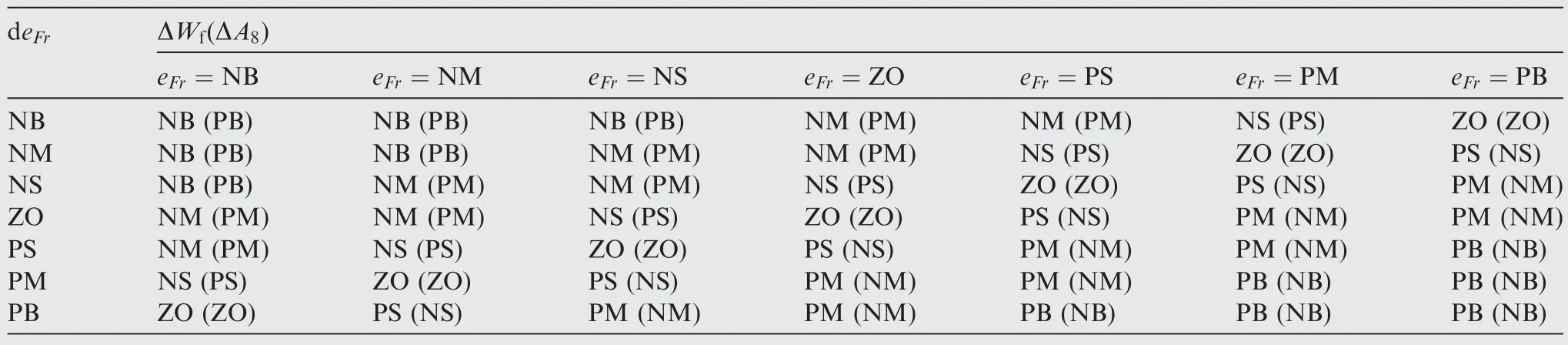
Table 3 Fuzzy control rules of output.

In this paper,both fuzzification and defuzzification adopt the method of multiplying by a scale factor,which is determined by simulation debugging.

The increment of the control variables obtained by the fuzzy system is used as the initial value of the SQP algorithm to avoid the situation of trapping into the local optimization due to the inaccurate predictive model or other reasons.

4.2.Design of aero-engine thrust predictive controller

Model predictive controller designed in this paper includes four parts: predictive model,online correction,rolling optimization and feedback correction.The structure of the controller is shown in Fig.10.The predictive model is used to predict the output of the engine.The input and output of the neural network can be seen in Section 3.

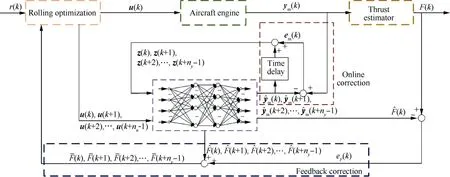
Fig.10 Structure diagram of controller.

Due to insufficient accuracy of the predictive model,external interference,etc.,an error maybe occurs between the actual output of the engine and the predictive output of the predictive model.The output errors of measurable parameters are used to correct the predictive output of the predictive model for the first predictive moment in the prediction horizon,and the corrected predictive output with time delay is served as input of the predictive model for the subsequent predictive moment in the prediction horizon.The output error is as follows.

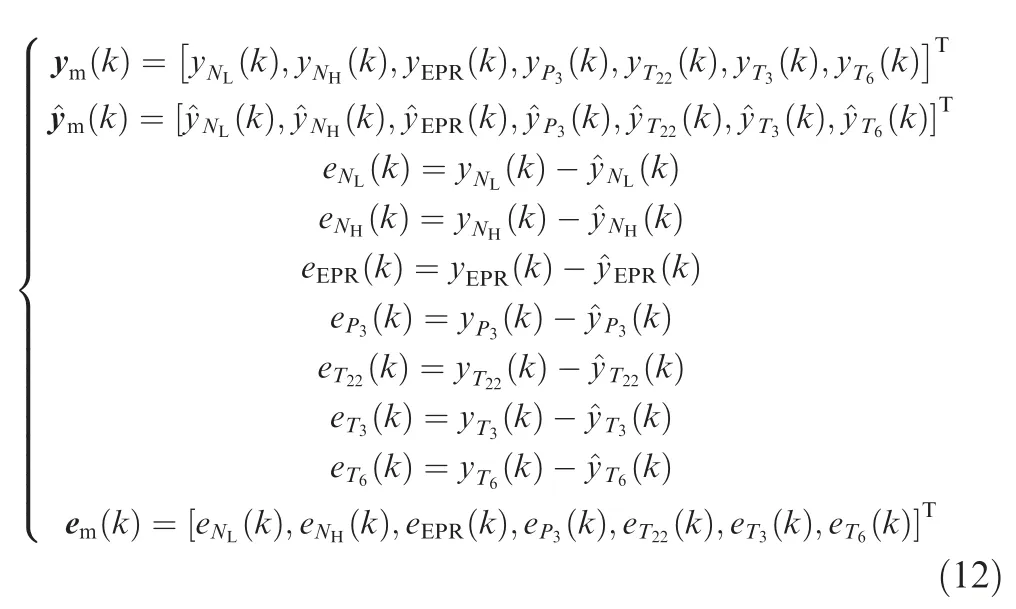
where ym（k）is the engine output,^ym（k）is the predictive output,and em（k）is the output error.

The mapping relationship of the neural network fornytime domains is

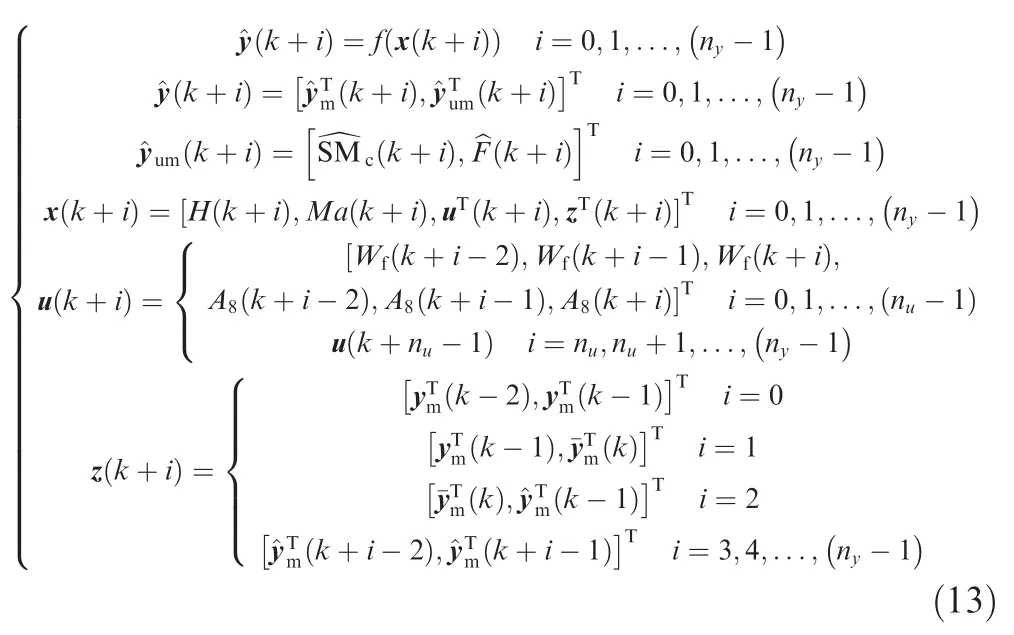
According to the error between the output of the thrust estimator and the predictive thrust,the predictive value in the prediction horizon is corrected,which is the feedback correction module.

whereF（k）is the output of the thrust estimator,is the predictive thrust.

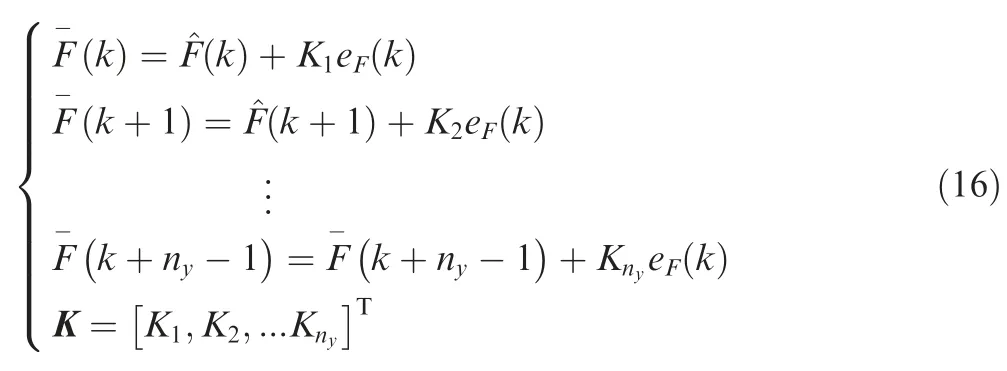
where K is the correction coefficient vector,and the value of the coefficient is generally within [0,1].

In this paper,the optimization problem is described as Eq.(10) with the constraints of Eq.(11).Fuzzy-SQP algorithm is used to solve the optimization which is described in Section 4.1.At timek,the sequence of control increment is obtained according to the solution of performance objective function,and the first value of the sequence is used to obtain the control value which is applied to the engine.Repeat the process at the next moment to form a rolling optimization.

5.Simulation and analysis

5.1.Effectiveness of online correction

In this paper,an online correction module is added on the traditional model predictive control structure.The following is a simulation to verify the effectiveness of online correction.Taking the ground point as an example,given the thrust commandr,the goal of the control is to track the command as fast as possible with the limited parameters within the safe range.And through several simulation experiments,the parameters are set as follows: prediction horizonny=3,control horizonnu=2,predictive error weight coefficient matrix Q=diag[1,1,1],control increment weight coefficient matrix R=diag [0.1,0.1,0.1,0.1],correction coefficient vector K=[1,1,1]T.The simulation result is shown in Fig.11.

Fig.11 shows that the control system that includes the online correction is faster to respond to the thrust command than the control system that does not include the online correction,and the steady-state tracking error is smaller,so it is effective for tracking control to add the online correction module.

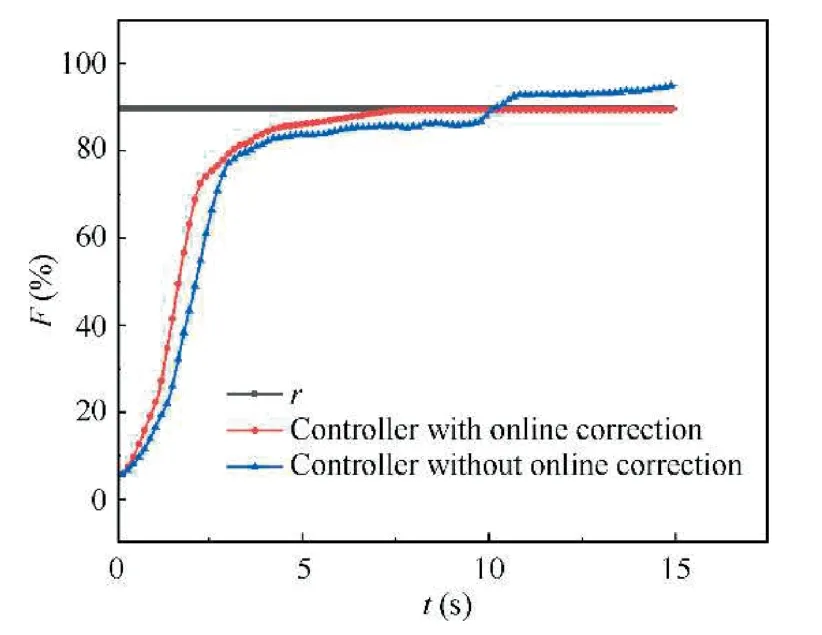
Fig.11 Comparison of thrust response with or without online correction.

5.2.Comparison of fuzzy-SQP based controller and other different controllers

Fuzzy-SQP algorithm is used as the optimization algorithm in the rolling optimization.It is compared with the SQP algorithm whose initial value is determined by the increment of the control variables at the last time.Also take the ground point as an example.The control purpose and the parameter settings in the control system are the same as those in the previous section.Only the optimization algorithm is distinguishing for simulation.The comparison of simulation result is shown in Fig.12.

As can be seen from Fig.12,once the optimization of a certain step traps into local optimization,since SQP adopts the increment of the control variables at the previous moment as the initial value,the whole control process will diverge and the control command cannot be tracked as shown by SQP1 and SQP2 in the figure (SQP1 and SQP2 are the SQP based controller which trap into different local optimization).But if the fuzzy-SQP is selected as the optimization algorithm,the situation of trapping into local optimization can be avoid and the controller can achieve good tracking performance.So,the fuzzy-SQP algorithm proposed in this paper has certain advantages.

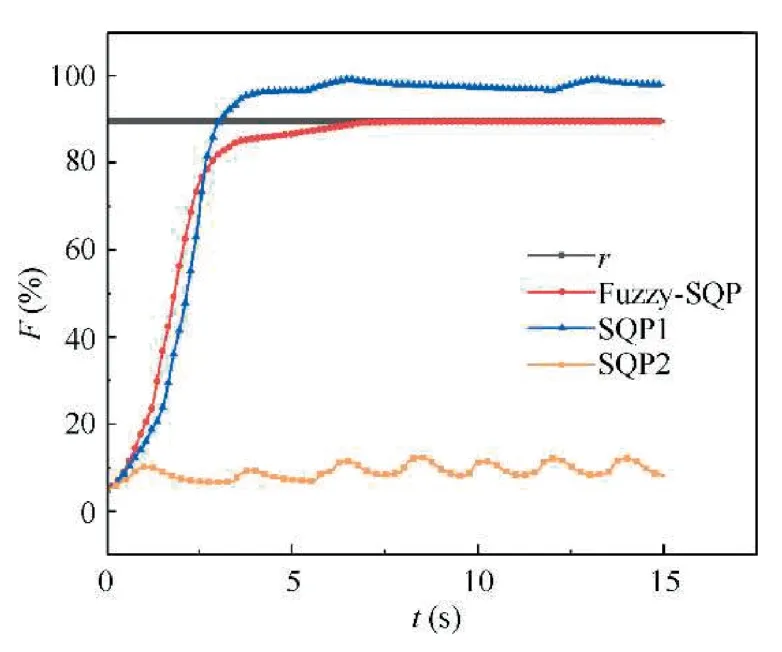
Fig.12 Comparison of thrust response of different optimization algorithms.

In addition to the comparison of fuzzy-SQP based NMPC and SQP based NMPC,the comparison simulation of the proposed controller and the traditional controller such as PI(Proportional Integral)controller is also carried out to illustrate the superiority of the proposed controller.The control purpose is the same as that in the previous section,and the parameter settings are set as follows by trial-and-error search.Wfcontrol loop:Kp=0.06,Ki=0.03;A8control loop:Kp=0.008,Ki=0.004.The simulation result is shown in Fig.13.

As can be seen in the Fig.13,compared with PI controller,the rise time of the proposed controller is shorter and the proposed controller has better dynamic performance.The reason why the dynamic performance of the response curve obtained by PI controller is not good enough may be that PI controller’s parameters are fixed,and it does not have the self-adaptive ability,while NMPC can optimize the control variables under the condition of satisfying the restriction.

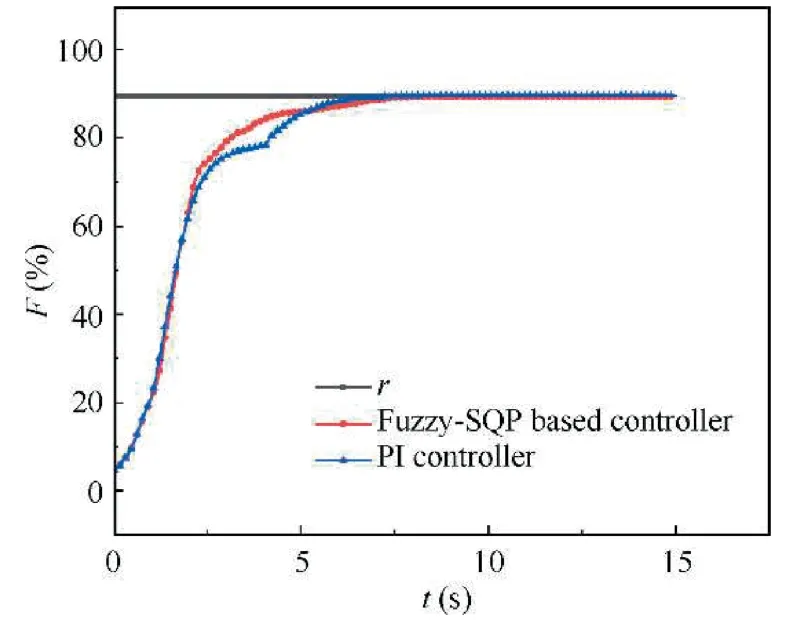
Fig.13 Comparison of thrust response of different controllers.

5.3.Tracking performance of control system

The designed controller is used to verify the thrust tracking performance,and the verification is performed at the point ofH=0 km andMa=0,H=3 km andMa=0.3,H=8 km andMa=1.2 andH=11 km andMa=1.5 respectively.The control purpose and the parameter settings are the same as those in the previous section.The simulation result is shown in Fig.14.

As can be seen from Fig.14,whether it is for the ground point or the other points,the designed control system has good tracking performance,and the steady state error is close to 0.

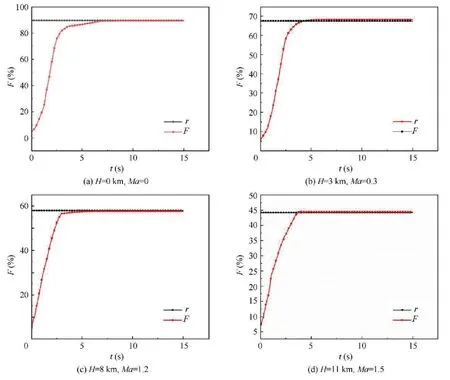
Fig.14 Thrust response curves.

5.4.Limiting performance of controller

The characteristic of model predictive control is that it can solve the optimization control under the condition of satisfying parameter limits.This section verifies the limiting performance of the designed control system.

Taking the ground point as an example,this section selects the low-pressure turbine exit temperatureT6as the limit value for verification.Given a thrust command beyond the safe operating range of the engine,change the limit value ofT6to verify whether the limiting performance is effective.The simulation results are shown in Fig.15.It can be seen from the figure that the designed system has good limiting performance.For example,if the limit value ofT6isl1in the figure,the response of engineT6l1always meets the limit.

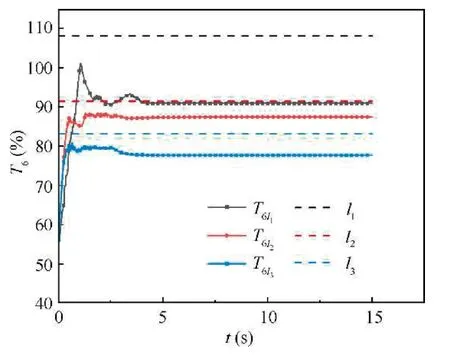
Fig.15 Response curves of T6 under different constraints.

5.5.Robust stability of controller

At present,the robust stability of the algorithm is mostly verified by simulations,mainly because the theoretical research of algorithm construction and control structure is too complicated.15The simulations considering measurement noise are carried out in this section to verify the robust stability of the controller.In general,the measurement noise can be approximated as Gaussian noise.32

Taking the ground point as an example,assuming that the Standard Deviations (SD) of measurement noise are 0.0015,0.003 and 0.01 respectively,the control purpose and the parameter settings are the same as those in the previous section.The simulation results are shown in Fig.16.

As can be seen from Fig.16,although the rise time of the system becomes longer with the increase of the amplitude of noise,it has a certain anti-noise ability,which can meet the control requirements with the limited parameters within the safe range,and the steady state error is close to 0.This can reflect that the system has certain robust stability.

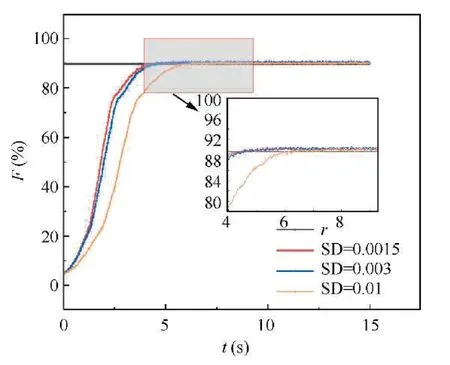
Fig.16 Response curves with noise of different amplitudes.

6.Conclusions

A nonlinear model predictive control method for direct thrust based on the fuzzy-SQP algorithm is proposed in this paper.The following conclusions can be drawn:

(1) The random forest algorithm is adopted to determine the input of BP neural network predictive model,aiming at simplifying network structure.

(2) For purpose of preventing from trapping into local optimization,fuzzy algorithm is used to determine the initial value of SQP.Based on fuzzy-SQP,the proposed controller has good tracking performance and meets the requirement of limits at the same time.In addition,the system also has a certain anti-noise ability.

(3) An online correction module is added to the traditional structure of model predictive control for the purpose of improving the accuracy of prediction of the predictive model.

(4) The comparison between the system with fuzzy-SQP and the system with SQP is carried out in this paper,the system with fuzzy-SQP possesses the faster response and the smaller steady state error.The comparison of fuzzy-SQP based NMPC and PI reveals that the proposed controller has better dynamic performance.

(5) In the following research,the accuracy of the predictive model is supposed to be improved by using more comprehensive data,which contains various working conditions of the engine.This paper does not focus on the real-time performance of the control system,and then we need to take measures to ensure the real-time performance of the system.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgements

This work was supported by the Fundamental Research Enhancement Project,China (No.2017-JCJQ-ZD-047-21).