Control and utilization of range-dependent beampattern with waveform diverse array radars

Ln LAN ,Guisheng LIAO,* ,Jingwei XU ,Shengqi ZHU ,Co ZENG ,Yuhong ZHANG

a National Key Laboratory of Radar Signal Processing,Xidian University,Xi’an 710071,China

b School of Electronic Engineering,Xidian University,Xi’an 710071,China

KEYWORDS FDA;Jammer suppression;Parameter estimation;Range-dependent beampattern;SAR imaging;Waveform diverse array radar

Abstract The transmit antenna beampattern of the phased array radar is only a function of angle,limiting its ability to discriminate the targets from the same direction.Recently,the waveform diverse array radars expand the angle-dependent beampattern to an angle-time-range-dependent three-dimensional function by modulating the frequencies/time delays/phases across different transmit antenna elements.In this respect,extra Degrees-of-Freedom (DOFs) in the range domain are achieved,which opens up an innovative way to fulfil the tasks with enhanced system performance by jointly using the angle and range information.This paper summaries the developments of waveform diverse radars,including the Frequency Diverse Array (FDA),the Space-Time-Circulating-Array (STCA),and the Element-Pulse-Coding (EPC) frameworks,with emphasis on the analysis of the range-dependent beampattern from the basic properties upon how it is controlled.Moreover,the most recent advances of utilizing such a range-dependent beampattern in target detection,parameter estimation and identifiability,clutter suppression,jammer suppression and Synthetic Aperture Radar (SAR) imaging are discussed.

1.Introduction

Phased array,with the advantages of flexible electronic beam scanning,strong jamming countermeasure,high-precision and high-reliability measurement,multi-function and multitask,has been extensively utilized in radio systems such as the communication,radar,sonar,astronomy,and navigation.1–4However,the transmit antenna beampattern is only a function of angle,which makes it difficult to distinguish two targets from the same direction.Waveform diverse array radar refers to an emerging radar framework,where the waveform comprises the modulation of an emitted signal with adaptation in several domains,such as spatial,temporal,spectral,and polarization,aimed at dynamically improving the radar performance for the particular scenario and tasks.5–7The waveform diversity has drawn much attention in radar and signal processing communities during the last decade.5,8–11Hence,the Degrees of Freedom (DOFs) of the system are increased,enhancing the ability of beam control and signal processing dimension of the system.Among the schemes of waveform diverse array radars,the Multiple-Input Multiple-Output (MIMO) radar has been proverbially studied from the aspects of waveform design criteria and system constraints,12–14optimization methods,15–17and its applications in detection,18–20tracking21–24as well as imaging.25–30Recently,modulations across the transmit antenna elements,performed in terms of the frequency,31time32,and phase,33are focused,where the extra DOFs in the range domain are obtained.Specifically,the concept of Frequency Diverse Array(FDA) has been proposed by introducing a frequency increment Δf,which is much smaller than the carrier frequency,among the transmit array,31,34–37which can generate an angle-time-range-dependent transmit antenna beampattern.Besides,the Space-Time Coding Array(STCA)has been introduced by shifting the transmitted signal across the array elements with a small time offset Δt,which is inversely proportional to the bandwidth.32,38,39It shares the property of wide angular coverage as seen in the MIMO radar.40–42Furthermore,the concept of Element-Pulse-Coding (EPC) has been inspired by extending the FDA to multiple transmit pulses.33,43,44In this respect,the research on the waveform diverse array radars is getting more in-depth,especially for the control and utilization methods of the range-dependent beampattern to further meet different application requirements.

In order to capture the technical development process of waveform diverse array radar,Fig.1 provides a graphic summary of the mentioned waveform diverse radar frameworks withMtransmit antenna elements,including the mathematical property of the beampattern,the features as well as the existing applications,where the detailed analyses of the literature are given in Sections 1.1 and 1.2,respectively.

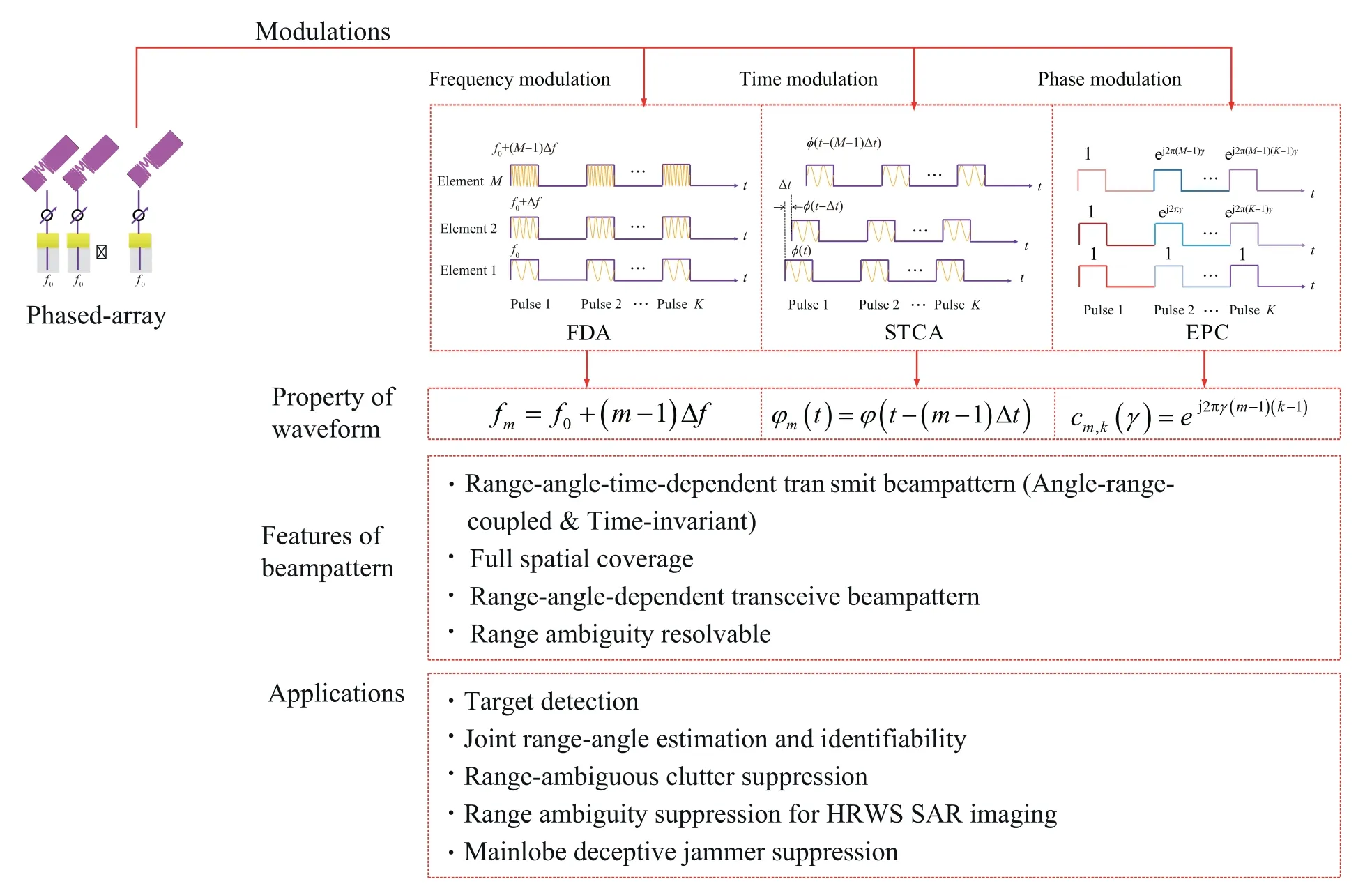
Fig.1 State-of-art developments of waveform diverse radars.

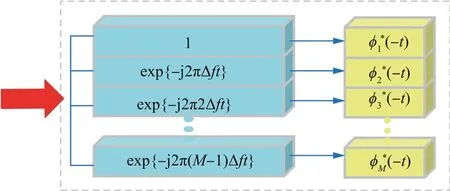
Fig.2 Signal processing at the receiver in FDA-MIMO radar.

1.1.Studies on beampattern

Capitalizing the property of range-dependent beampattern,the FDA radar has been attracting a lot of research interest in radar and signal processing communities during the last decade.According to Ref.45,the FDA radars can be categorized into two groups,i.e.,the coherent FDA and orthogonal FDA.The same baseband waveform is adopted for all array elements in coherent FDA,where the range-angle-dependent transmit beampattern is obtained.In contrast,orthogonal waveforms are transmitted in the orthogonal FDA radar(also known as the FDA-MIMO radar).Consequently,a rangeangle-dependent Two-Dimensional (2D) joint transmitreceive beampattern,i.e.,the transceive beampattern,is realized after separating the transmitted waveforms with matched filters in the receiver.46The properties of the beampatterns for coherent FDA and FDA-MIMO are discussed as the following two aspects.

(1) In coherent FDA,although the range information is obtained,the ‘S’-shape range-angle-dependent transmit beampattern is unfavorable for target localization in practice.Firstly,the angle and range are coupled at a fixed time instant using the linearly increased frequencies.47–49In this regard,the transmit energy is distributed in the joint range-angle domain,resulting in some ambiguities for target localization.50–52Besides,the beampattern is time-variant,indicating that any radiation/waveform/peak/null experienced at a certain point of range will travel to any point along the same direction.53–56To overcome the rangeangle-coupling,the frequency increments were designed using logarithmically increasing frequency increment,57,58intelligent algorithms,59–61windowed frequency offsets,62,63Costas sequence,64and randomly assigned frequencies.65Moreover,the closed form expression of the range-angle decoupled beampattern is derived mathematically in Ref.66.To overcome the time-variant problem,the Time-Modulated Optimized Frequency Offset(TMOFO)method was proposed in Ref.67.Besides,an Compensated TMOFO(C-TMOFO)and time-window C-TMOFO were developed in Ref.68,where a time-invariant spatial beam was generated in a short range.Moreover,methods resorting to sparse time-modulated optimized offsets69and polarizationsensitive subarray-based scheme70were proposed.However,the conclusion was drawn in Ref.71that the transmit beampattern in FDA cannot focus on some specific spatial positions and last for some specific time.In this regard,the exact relationships with respect to (w.r.t.) time-range and frequency-phase pairs were analyzed,and a correction analysis about the factor of time was presented in Ref.72.

(2) As for the range-angle-dependent transceive beampattern in FDA-MIMO radar,the mainlobe of the transceive beampattern is focused on the positions of the target with specific range and angle45.In this respect,aimed at forming a range-angle-dependent transceive beampattern for FDAMIMO radar with desired responses,methods were developed to control the response of the beampattern.73–75In Refs.73,74,the null regions of the transceive beampattern can be broadened by imposing multiple artificial interferences with prescribed powers,where the powers of the artificial interferences can be derived in closed form according to the predefined null depths.Furthermore,in Ref.75,a desired transceive beampattern was formed with a flat-top mainlobe,broadened nulls,and low sidelobes by combining the weight vector orthogonal decomposition and oblique projection.

1.2.Studies on applications

Indeed,the mentioned range-dependent beampattern provides extra DOFs n the range domain that can be exploited to boost the performance of surveillance systems,in terms of target detection,parameter estimation and identifiability,clutter/mainlobe deceptive jammer suppression as well as Synthetic Aperture Radar (SAR) imaging,which can be summarized in the following aspects.

(1) Target detection

A simplified signal model for detection in the FDA-MIMO radar was analyzed in Ref.76,where the assumptions of the absence of clutter as well as knowledge of the target range and interference covariance matrix were considered.In Refs.77–79,a conic model for the signal component was studied with the knowledge of the interference-plus-noise covariance matrix.To obtain the maximum likelihood estimate in FDA-MIMO radar,three different optimization strategies were pursued including the Semidefinite Programming (SDP),the grid search,and the Newton-based refinement procedure.80In Ref.81,the FDA radar model was used for blind-Doppler target detection in the environment of mainlobe clutters by exploiting the Doppler-Spreading (DS) effect.Moreover,the Space-Range-Doppler Focus (SRDF) approach was proposed in Ref.82for moving target detection and classification.The detection performance of the FDA-MIMO radar using the multi-pulse detector was analyzed when targets conform to Swerling I and Swerling II model.83

(2) Parameter estimation and identifiability

Capitalizing the additional DOFs of the range-dependent beampattern,many researchers have studied the joint angle and range estimation for a single target in FDA-MIMO radar.In Ref.84,the method to localize the range and angle of targets was proposed in a double-pulse FDA radar with an Uniform Linear Array(ULA) configuration,where two pulses with zero and non-zero frequency increments were transmitted,respectively.Then,the azimuth angle and slant range of targets can be estimated according to the peaks of the beamforming.In Ref.85,the unambiguous estimates of the angle and range were achieved in the receive spatial domain and joint transmit-receive spatial domain,respectively.The theoretical performance analysis was provided in Ref.86,where the Crame´r-Rao lower Bound (CRB) and Mean Square Error (MSE) expressions in MUltiple SIgnal Classification (MUSIC)-based algorithms were derived in FDA-MIMO radar.To reduce the computation complexity of the 2D MUSIC algorithm,the one-dimensional MUSIC algorithm was proposed to estimate the angle and range in monostatic FDA-MIMO radar.87In Ref.88,a cognitive target tracking approach was developed by angle-range-Doppler estimation in the Transmit Subaperturing Frequency Aiverse Array (TS-FDA) radar.The algorithm based on gridless compressed sensing was proposed in Ref.89to estimate the range and angle jointly in FDAMIMO radar by solving the 2D Atomic Norm Minimization(ANM)problem resorting to the Accelerated Proximal Gradient (APG) algorithm.In Ref.90,a two-stage estimation method was proposed via the Estimating Signal Parameter via Rotation Invariance Technique (ESPRIT)algorithm in FDA-MIMO radar for unambiguous range and angle estimates.Furthermore,the angle and incremental range estimation with a FDA-MIMO radar with a single data snapshot was studied in Ref.91,where three techniques were designed including the coordinate descent algorithm and the adaptive monopulse criterion(employing either real or complex slope/bias corrections).What’s more,by resolving the range ambiguity in EPC-MIMO radar,an enhanced parameter estimation approach was developed in Ref.33to estimate the angle and range region number of the target.Considering multiple targets,the parameter identifiability,i.e.,the maximum number of targets that can be uniquely identified,is a key issue.Actually,the waveform diversity in the transmitter enables to significantly improve the capabilities to identify target parameters,which is common in MIMO,FDA-MIMO,and EPC-MIMO radars.92The researchers have studied the parameter identifiability of MIMO radar intensively.In Ref.93,the joint estimation of DODs and DOAs for multiple targets using a single pulse in bistatic MIMO radar was focused based on the subspace algorithms,and the identifiability limit was analyzed.A comparison of the DOA parameter identifiability between the MIMO radar and the phased array radar was carried out in Ref.94,where the comparable performance was achieve using the conventional transmission and MF estimators for a single target,and the MIMO radar outperforms the phased array radar for multiple targets.Besides,the parameter identifiability for phased-MIMO radar was studied in Ref.95,96,where the subarray configuration was involved to increase the parameter identifiability up to the number of subarrays compared with the conventional phased array radar.Moreover,the concept of coprime FDA was proposed in Ref.97by combining the FDA with coprime sampling,98,99where the difference coarray can be used to circumvent the limitation of physical sampling.The multitask Bayesian compressive sensing approach was utilized in Ref.97to improve the performance of DOArange resolution,localization accuracy,as well as the ability to resolve multiple targets.Besides,the second-order statistics was utilized in Ref.98to construct the location and frequency of the coprime difference sets of coprime FDA in the virtual domain,achieving a larger array aperture and higher DOFs.Moreover,the atomic-norm optimization was implemented in Ref.100,which can localize more targets than the DOFs provided by the physical sensors.

(3) Clutter suppression

The FDA-MIMO has the ability to distinguish echoes corresponding to different range ambiguity regions,which can be utilized in ambiguous clutter suppression.The Space-Time Adaptive Processing (STAP)-FDA was established in Ref.101to discriminate the clutter with range ambiguity in the spatial frequency domain,and a method based on the Secondary Range Dependence Compensation (SRDC)was performed to separate them.Furthermore,the joint clutter and false targets suppression was investigated in Ref.102,where the false targets were firstly suppressed by using the subspace projection technique,and both the clutter and suppressive jamming signals were mitigated subsequently.In Ref.103,a vertical FDA in a planar array was explored to resolve the range ambiguity in STAP radar resorting to vertical spatial frequency compensation and pre-STAP filtering.In this respect,the range-angle-Doppler processing procedure was performed by exploiting the DOFs in transmit-receive-pulse Three-Dimensional(3D) domains in the FDA-MIMO radar,104where an enhanced three-dimensional localization technique was proposed to reduce the dimensions of the processor and suppress clutter in practical applications efficiently.Besides,an enhanced 3D joint domain localized STAP method,incorporated with deceptive jamming pre-whitening in the transmit-receive spatial domain,was proposed to extract unpredictable deceptive jamming samples efficiently in the background of true targets and ground clutter.105Moreover,a two-stage adaptive clutter suppression method was proposed in Ref.106,where a novel multi-waveform based adaptive beamforming was proposed and an auxiliary channel based space-time adaptive processing approach with range dependence compensation was developed.In Ref.107,the bistatic FDA-MIMO STAP radar was developed,where the clutter ridges from different range regions were discriminable in 3D space by properly designing the frequency increments.

(4) Mainlobe deceptive jammer suppression

Because the modulation is performed across the transmit array elements in waveform diverse array radars,the true and false targets,which are generated in Digital Radio Frequency Memory(DRFM),can be distinguished in the joint transmit-receive spatial domain.In this respect,a lot of methods have been developed in FDA-MIMO radar to suppress the mainlobe deceptive jammers.The range-angledependent adaptive matched filter was designed in Ref.108to suppress the false targets due to range mismatch.However,the signal model in Ref.108is just a special case with the absence of time delay term.Furthermore,the signal model was modified in Ref.109,where a sample selection method based on subspace projection was proposed to suppress the jammers.Besides,the time delays of the false targets were analyzed in Ref.110.Considering the limitation that it is not practical to find perfectly orthogonal waveforms for all Doppler and delay pairs,the transmission of random polyphase codes was considered in Ref.111.Moreover,a ‘‘lowrank+low-rank+sparse” decomposition model was employed to extract the desired signal and suppress both barrage and burst jammers in Ref.112,where a two-step ‘‘Go Decomposition”(GoDec)method by alternating minimization was devised.In Ref.113,a Polarisation and Frequency Diverse MIMO(PFD-MIMO)system was proposed,where improved deceptive jamming suppression performance can be achieved when both the transmitting polarisation and the frequency increment are optimised.However,it is not easy to select sufficient samples with data-dependent beamforming,because the training samples from range bins are no longer independent and identically distributed.To solve the problem,a robust Nonhomogeneous Sample Detection(NSD) method was proposed in Ref.114.Moreover,the data-independent beamforming was employed in Ref.115by nulling the false targets at nulls of the equivalent transmit beampattern w.r.t.the true target with an appropriate frequency increment,and the nulls were broadened to enhance the robustness in the presence of practical mismatch.Furthermore,the jammer suppression was considered in EPCMIMO radar by nulling the false targets at the equivalent transmit beampattern.116,117Moreover,the method based on Preset BeamPattern Synthesis (PBPS) was developed to enhance the robustness of suppression performance in the presence of direction mismatches.116

(5) SAR imaging

The application of FDA in SAR imaging was explored in Ref.118–120,where the azimuth resolution can be improved by utilizing the range-dependent beampattern.Along the same line of reasoning,the range resolution could be enhanced with multiple transmit antennas.121The rangeangle imaging of targets was achieved by performing the transceive beamforming in Ref.121,where the nonuniform FDA was designed as the transmitter and the uniform phased array as the receiver.To mitigate the conflict between range and Doppler ambiguities,a spaceborne FDA-SAR system framework was developed to achieve High-Resolution and Wide-Swath imaging (HRWS) imaging,122where the range ambiguity can be resolved by utilizing the Range Dependence Compensation (RDC) technique and exploiting the extra DOFs in the range domain.Besides,a corresponding range-angle-dependent transmit beamformer was designed to extract the spectrum component of each ambiguous region,which can be rearranged to comprise the desired unambiguous signal.123Moreover,as for multichannel SAR-Ground Moving Target Indication (SARGMTI),the phase difference between channels caused by image coregistration and channel phase errors will deteriorate the performance of the moving target radial velocity estimation.124To solve the problem,a method to estimate radial velocity in FDA-SAR was proposed in Ref.125with a linear relationship between the interferometric phase among channels and the Doppler frequency.Furthermore,in Ref.44,a novel phase coding technique was employed in both spatial channels and slow time pulses.With the coding scheme,the desired echoes from the presumed range region can be extracted and the undesired echoes from other rangeambiguous regions can be suppressed by designing the coding and the transmit beampattern.

Other applications,such as target tracking,126–131communications,132–136etc.,have verified the superiorities of the range-dependent beampattern with waveform diverse array radars.To sum up,the technique features,the functions and the relationships of the mentioned applications using the waveform diverse array radars are listed in Table 1.

Table 1 Techniques in applications of waveform diverse array radars.

As the range-dependent beampattern has been widely investigated and utilized in many applications,summaries about the principles and applications about the FDA radar can be found in Refs.35,36,45,137–140.Because FDA radar is only a representative case among the waveform diverse array radars,instead,this paper provides an overview of the range-dependent beampattern with the waveform diverse array radars,from the basic principles upon how it is controlled to be applied in different practical applications being explored in research.On the one hand,this paper aims to make a survey on the control and utilization methods of the range-dependent beampattern.Given that,this paper offers an investigation of the state-of-the-art advances,especially during the latest three years.On the other hand,potential developments on novel frameworks and signal processing methods related with the control and utilization of the range-dependent beampattern are encouraged for whom may have interest.

The organization of this paper is provided as follows.Section 2 is to introduce the fundamentals of the waveform diverse array radars and their mathematical signal model.Section 3 illustrates the range-dependent beampatterns of the waveform diverse array radars including the transmit beampatterns and the transceive beampatterns.Section 4 provides an overview on how to control the range-dependent beampattern with the dependence on the angle and time,where the range-dependent properties both within the pulse and between pulses are analyzed.In Section 5,typical applications of the range-dependent beampattern are introduced,including the adaptive target detection,the joint parameters estimation,the range-ambiguous clutter suppression,the mainlobe deceptive jammer suppression,as well as HRWS SAR imaging,whereas the experimental systems for waveform diverse array radars are addressed in Section 6.Finally,conclusions and potential future studies are discussed in Section 7.

Notations:Boldface is used for vectors x(lower case)whosen-th entry isx（n）,and matrices A(upper case)whose（m,n）-th entry isAm,n.The transpose,the conjugate,and the conjugate transpose operators are denoted by the symbols（·）T,（·）*,and（·）†,respectively.I,0,and 1 denote respectively the identity matrix,the matrix with zero entries,and the vector with all elements being one (their size is determined from the context).CN,RN,and CN×Mrepresent the sets ofN-dimensional vectors of complex numbers,N-dimensional vectors of real numbers,andN×Mcomplex matrices,respectively.For any x ∈CN,‖x‖2and ‖x‖Fdenote the Euclidian norm and Frobenius norm,respectively.⊙,⊗,and * indicate the Hadamard product,the Kronecker product,and the convolution,respectively.The letter j represents the imaginary unit.[a,b] indicates a closed interval of R1.Finally,for any real numbery,the function sign（y）=-1 ify＜0 and 1 ify≥0.

2.Signal model of waveform diverse array radars

In this section,let us consider a uniform linear array configuration consisting ofMantenna elements.In waveform diverse array radars,frequency/time/phase modulations between adjacent elements are performed in FDA,STCA and EPC,respectively(see Fig.1)).The transmit modulations and the practical transmit-receive mathematical models of different configurations are studied respectively as follows.

2.1.FDA

In FDA radar,the frequency increment Δfis introduced between adjacent antenna elements with the first being the reference.Hence,the carrier frequency of them-th transmit element is80

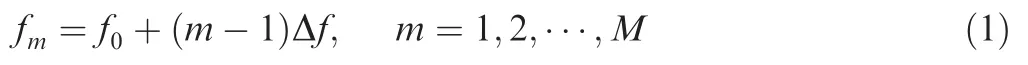
wheref0denotes the reference carrier.

Then,the transmitted signal of them-th antenna element is given by

where φm（t）is the transmitted waveform from them-th element in FDA radar.Note that we have the following discussions on the specific transmitted waveform:

(1) For coherent FDA radar,the identical waveform,such as the Linear Frequency Modulation (LFM) signal,i.e.,φm（t）=exp｛jπμt2｝,m=1,2,···,M with μ the rate,is transmitted.

(2) For FDA-MIMO radar,where the orthogonal waveforms are considered,we have the orthogonal condition,i.e.,=0,l ≠m,∀τ with τ being an arbitrary time and Tpbeing the pulse duration,respectively.[102]

(3) As for non-perfectly orthogonal waveforms in practice,the phase-coded waveform,which consists of multiple subpulses in each transmitted pulse,is usually considered.[115,111]It is assumed that a total ofKpulses are transmitted during the coherent processing interval.Under the narrowband assumption,for a target with angle θ and rangeR,the reflected signal received by then-th element is expressed as

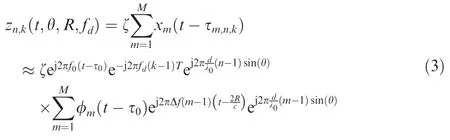
In particular,we have the following discussions for the detailed expressions of the total received data y (in the background of Gaussian noise n):

(1) For the receive vector of a single target located at θ0and R0with the velocity v0,it is expressed as

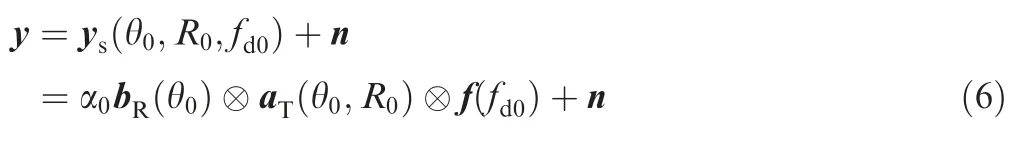
wherefd0=is the Doppler frequency.

(2) Considering multiple targets,the received data withQtargets is

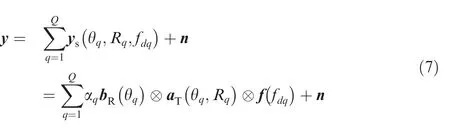
where θq,Rq,andfdq=indicate the angle,range,and Doppler frequency of theq-th target,respectively,andvqis the velocity of theq-th target.

(3) Consider an airborne radar with ground clutter,the received data is[102]

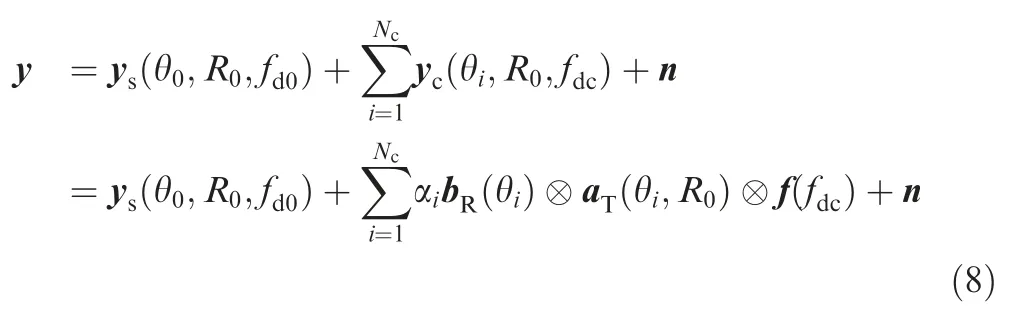
whereNcdenotes the number of statistically independent clutter patches for the iso-range,andfdcis the Doppler frequency of the ground clutter.

(4) In complex environment where both the mainlobe deceptive jamming signals (i.e.,the false targets) and the clutter exist,it yields

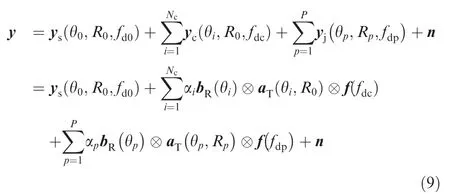
whereRqandfdp=indicate the range and Doppler frequency of thep-th false target,respectively,andvpis the velocity of thep-th false target.

2.2.STCA

In STCA radar,it is assumed that an identical LFM waveform φ（t）is transmitted with a small time shift Δtcirculating across the array elements.In this regard,the baseband waveform corresponding to them-th array element can be written as[42]

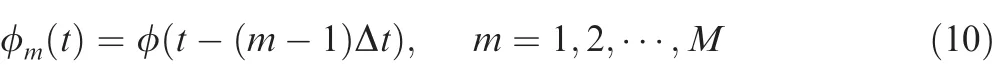
where the time offset is assigned as the reciprocal of the bandwidthBw,i.e.,Δt=1/Bw.It follows the transmitted signal of them-th element as

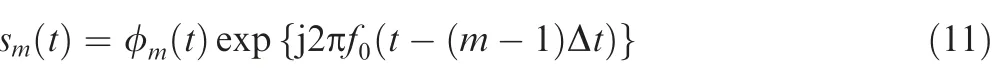
Under the assumption of narrowband,the signal received by then-th element is expressed as

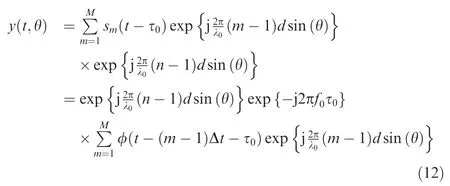
The received signal is processed through an angle-timedependent matched filter for every possible specific direction,i.e.,

Then,the output function is expressed as

2.3.EPC

Moreover,the EPC scheme is inspired from the FDA radar by extending the signal model to multiple transmit pulses.In this respect,the transmitted signal from thek-th pulse is expressed as

where φm（t）denotes the transmitted signal of them-th element which has been illustrated in Eq.(2) and the approximation holds when=f0T∈Z+,by observing from the equation,it is found that the phase term,i.e.,ej2π（m-1）Δf（k-1）Tis introduced.Specifically,it varies in both the spatial channels and slow time domain,which serves as an ‘flag’ to discriminate echoes from different transmit pulses.In this regard,we can perform element-pulse-coding with a coefficient,i.e.,instead of using an frequency increment to separate echoes corresponding to different range ambiguity regions,where the EPC factor is given by[33,43,44]

In this respect,the EPC scheme is combined with the MIMO radar to tackle the problem of range ambiguity.[33]In EPC-MIMO radar,the signal received by then-th(n=1,2,···,N) element which is transmitted by them-th one under the narrowband assumption is given as[43]

After multiplied by e-j2πf0t,the received signals pass through a bank ofMmatched filtershl（t）=（-t）(l=1,2,···,M)(see Fig.3)) on each receive channel to separate the transmitted waveforms.[43,117] Subsequently,the decoding procedure is performed,where the decoding vector is expressed as

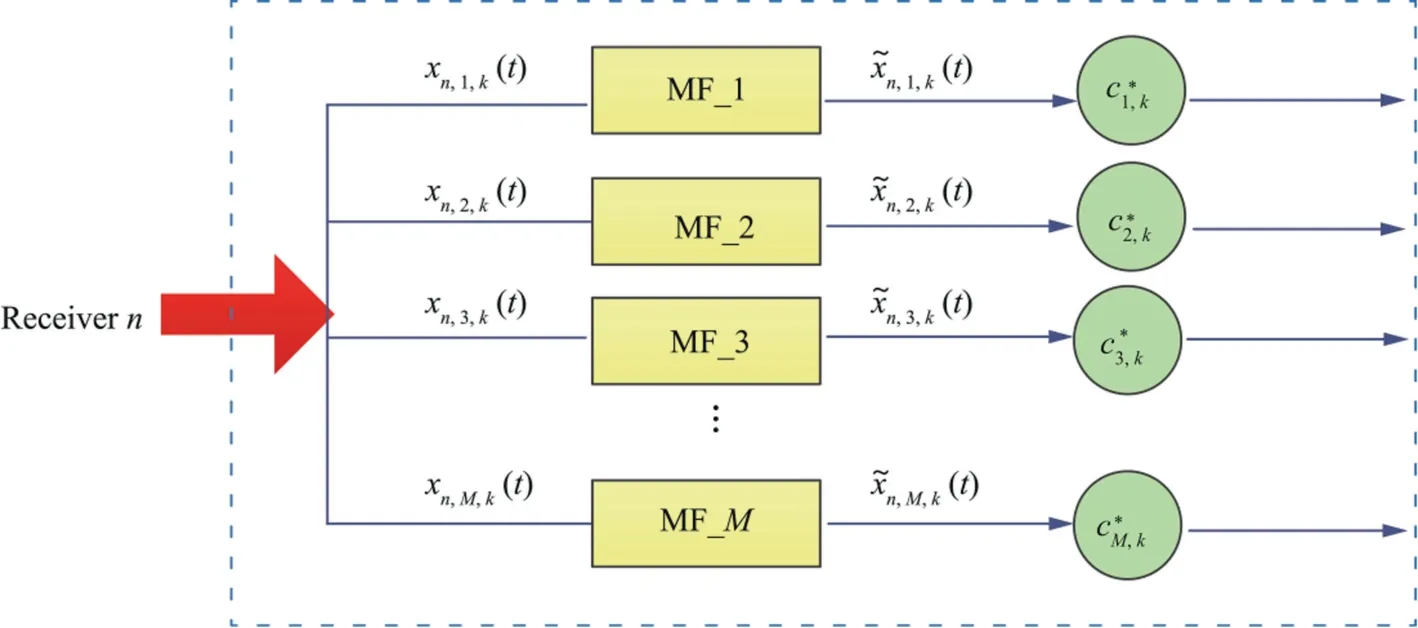
Fig.3 Signal processing procedures in the n-th receive channel w.r.t.the k-th pulse..

Then,by stacking the received signals into anMN×Kspace-time snapshot,the echoes of the target fromKpulses are written as[117]

3.Range-dependent beampattern of waveform diverse array radars

This section provides an introduction of the range-dependent beampattern with waveform diverse array radars,including the transmit beampattern and the joint transmit-receive beampattern,with emphasis on the angle-range-time-dependent property of the FDA radar.

3.1.Transmit beampattern

For simplicity,only the array factor of the antenna beampattern is considered.For a far-field target with angle θ and rangeR,the transmit beampattern in FDA radar with an all-one weight vector can be expressed as45,47,75

where τm=and≪1 is considered for the assumption.It is observed that in FDA radar,the expression of the beampattern is a 3D function of range,angle and time.Figs.4(a)-(c)illustrate the corresponding 2D beampatterns with continuous wave system by fixing the range,time and angle,respectively.As analyzed in Ref.45,for a fixed rangeR,Fig.4 (a) indicates the electric distribution at different angles and time instants on the sphere with the rangeR.Besides,as shown in Fig.4 (b),the range-angle-dependent beampattern at a fixed time instant illustrates the electric intensity at different angles and ranges.Fig.4(c)shows the electric distribution for θ=0°,where the magnitude at a certain range indicates that the beampattern in FDA radar is time-instant.In other words,the response corresponding to any spatial position experiences the mainlobe and sidelobes periodically.Moreover,the periodicity is related with the frequency increment Δf.Particularly,the periods of the transmit beampattern w.r.t.the range,time and angle are derived asandrespectively,wherekis the wave number.45,54

Fig.4 Range-angle-time-dependent transmit beampattern in FDA with continuous wave system.[45]

Moreover,the transmit beampattern of the STCA radar can be written as

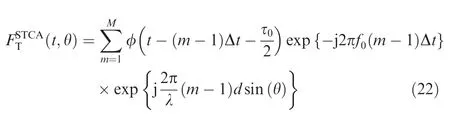
which is presented in Fig.5.Similar to the FDA radar,the characteristics of the time-angle-dependency indicate that the response for any position is time-variant.Actually,different frequencies correspond to different spatial angles in STCA radar,in which the phase difference between two adjacent Tx elements for a specific time instant is expressed as

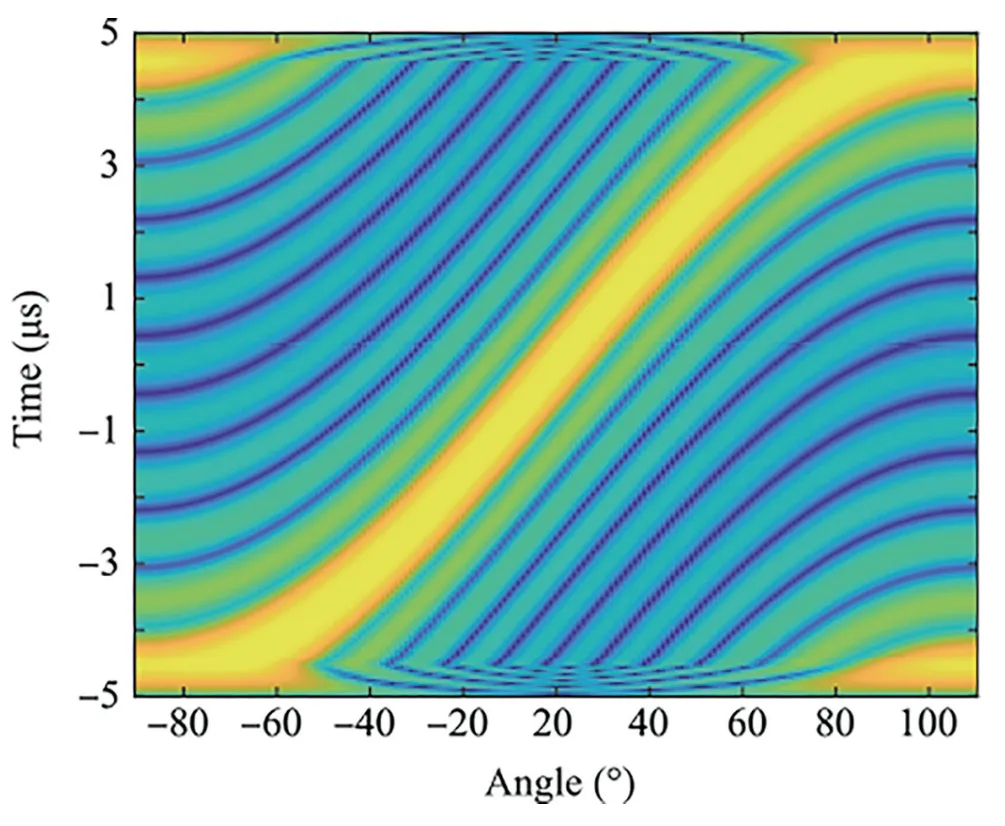
Fig.5 Transmit beampattern in STCA radar..

In pulse radar system,the transmit beampattern of FDA is written as

The comparison of the transmit beampattern at a fixed time instant among the phased array,the FDA and the MIMO with pulse radar system is illustrated in Fig.6,where the total transmit power and the bandwidth are fixed for a fair comparison.It can be observed that the transmit beampattern of the phased array radar is angle-dependent with a focused mainlobe,where an isotropic electric field w.r.t.angle is achieved.34,35The beampattern of FDA is dependent on the range and angle,where the energy is regularly distributed in the range domain;however,the transmit gain is reduced toMwhile the transmit gain isM2in phased array radar because the mainlobe is scanned automatically in the angle domain.45Moreover,the transmit beampattern cannot be formed in the MIMO radar due to its diverse waveforms corresponding to different elements,and the transmission power is evenly distributed.In other words,assuming that the total transmit power is exactly the same for different radar frameworks,including the phased array,MIMO and FDA,the transmit power is focused at a certain angle in phased array radar,while the power of MIMO radar is uniformly distributed in angle and time domains.In contrast,the transmit power is focused within a short time while scanned in the entire pulse in FDA.Furthermore,its transmit power is evenly distributed in the full spatial domain,which is equivalent to compressing the entire power in a short time in any direction.

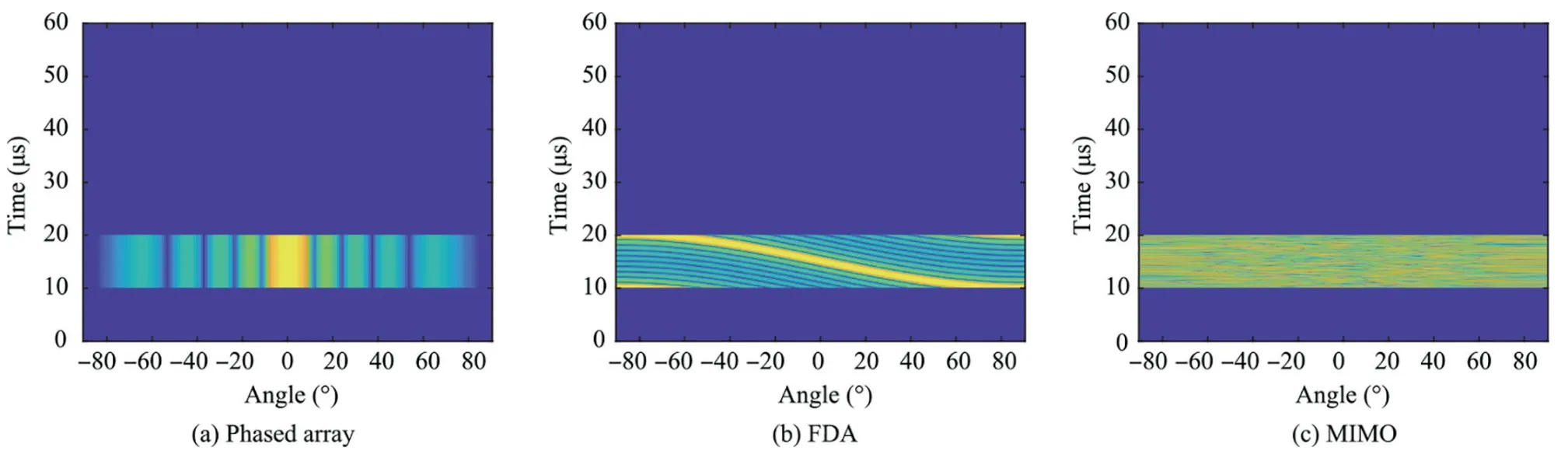
Fig.6 Comparison of transmit beampatterns among phased array,FDA and MIMO with pulse radar system.

3.2.Transceive beampattern

3.2.1.Beampattern characteristics within pulse

Firstly,the property of the beampattern within the pulse is investigated.Considering the coherent FDA with pulse radar system,the transmitted signal from them-th element is given by

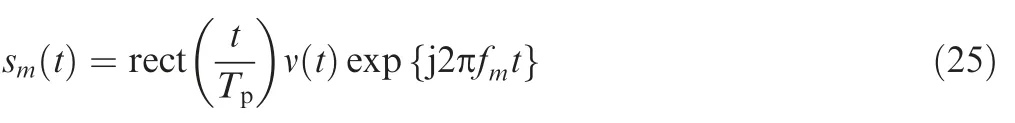
where ν（t）represents the transmitted waveform such as the LFM signal.Then,it follows the signal received by then-th(n=1,2,···,N) element as

where the corresponding receive beampattern is given by

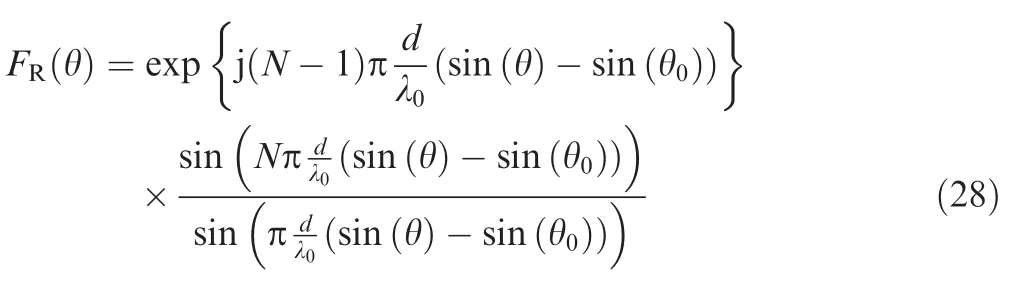
It is obvious in Eq.(28)that the receive beampattern of the coherent FDA radar is identical with that of the phased array radar,which indicates that the frequency diversity is only performed in the transmitter.Then,the joint transmit-receive beampattern for coherent FDA can be further expressed as[45]

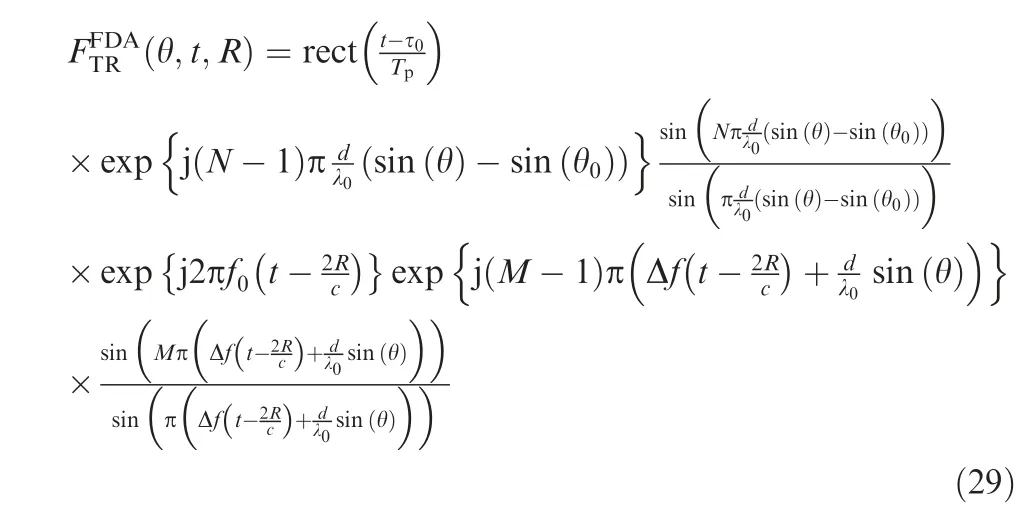
Hence,given by the data-independent weight vector,which is point at the target with wTR（θ0）=bR（θ0）⊗aT（R0,θ0）,the joint transmit-receive beampattern (namely the transceive beampattern)of the FDA-MIMO radar can be expressed as[75]

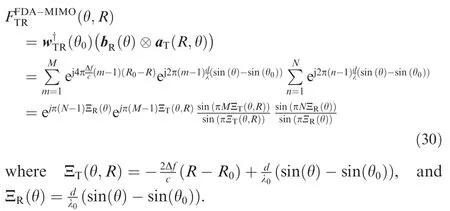
The comparison of the joint transmit-receive beampatterns between the coherent FDA and FDA-MIMO radars is displayed in Fig.7.Inspection of Fig.7 (a) highlights that at any time instant,the energy is focused at a point by performing the conventional receive beamforming with a presumed angle in coherent FDA.However,the joint transmit-receive beampattern in coherent radar is time-variant.In contrast,as shown in Fig.7 (b),owing to the procedure of digitally mixing with e-j2π（l-1）Δftin FDA-MIMO radar,the equivalent transmit steering vector aT（θ0,R0）is time-independent.[75]Hence,the range and angle information can be jointly achieved in the FDAMIMO radar,which will be discussed in details in Section 4.

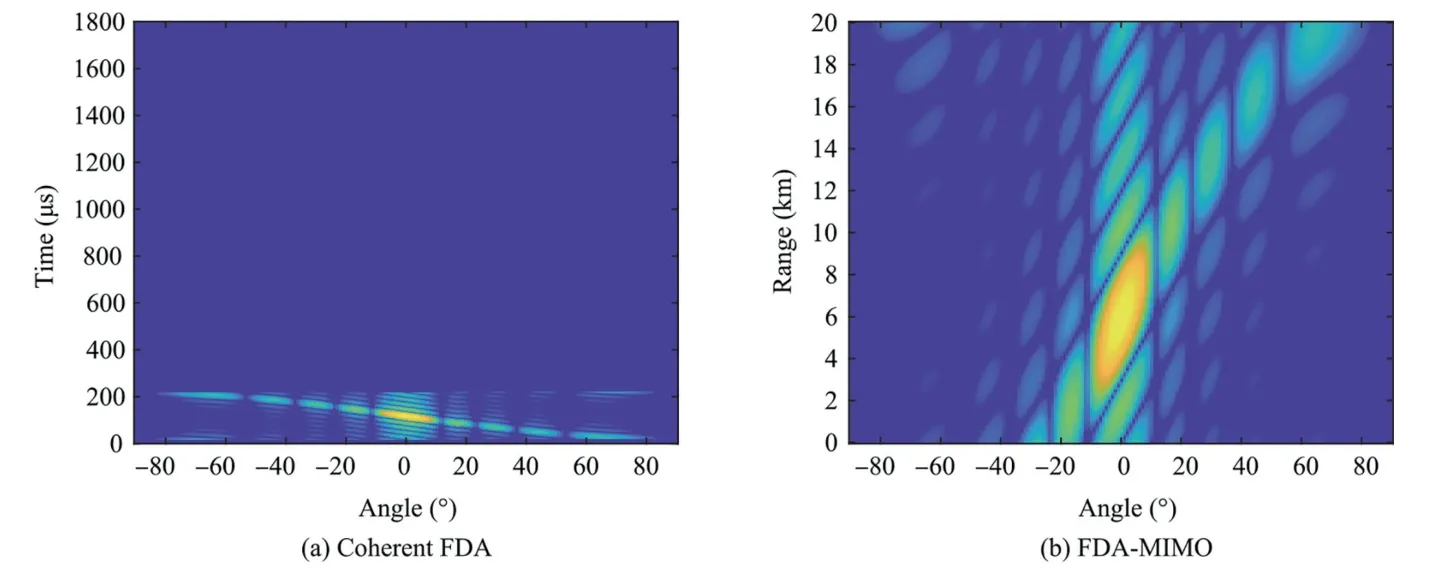
Fig.7 Comparison of joint transmit-receive beampatterns..

3.2.2.Beampattern characteristics across different pulses

Furthermore,considering multiple transmitted pulses,where the ambiguous range is considered,the beampattern across different pulses of the EPC radar is range-dependent.

It follows the normalized equivalent transmit beampattern as[43]

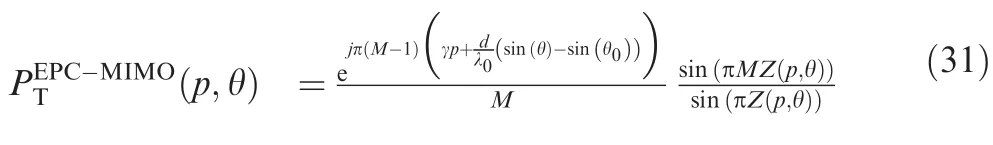
whereZ（p,θ）=γp+It is observed that for different numbers of delayed pulsesp,a phase term related with the coding coefficient γ exists,which results in a deviation of the mainlobe.More specifically,Fig.8 displays the equivalent beampatterns corresponding to different range ambiguity regions in EPC-MIMO radar.It is observed that a spatial‘flag’is introduced after waveform separation and decoding,which can discriminate echoes corresponding to different range ambiguity regions.In other words,the equivalent transmit beampatterns have different mainlobe directions (also known as different spatial directions),which correspond to different range ambiguity regions.Note that different from the FDA and STCA,the range-dependency of the beampattern is illustrated across the pulses;however,the energy of the equivalent transmit beampattern is focused within each pulse in EPCMIMO radar.Furthermore,the full spatial coverage is obtained by utilizing the slow time resources (i.e.,multiple transmitted pulses).

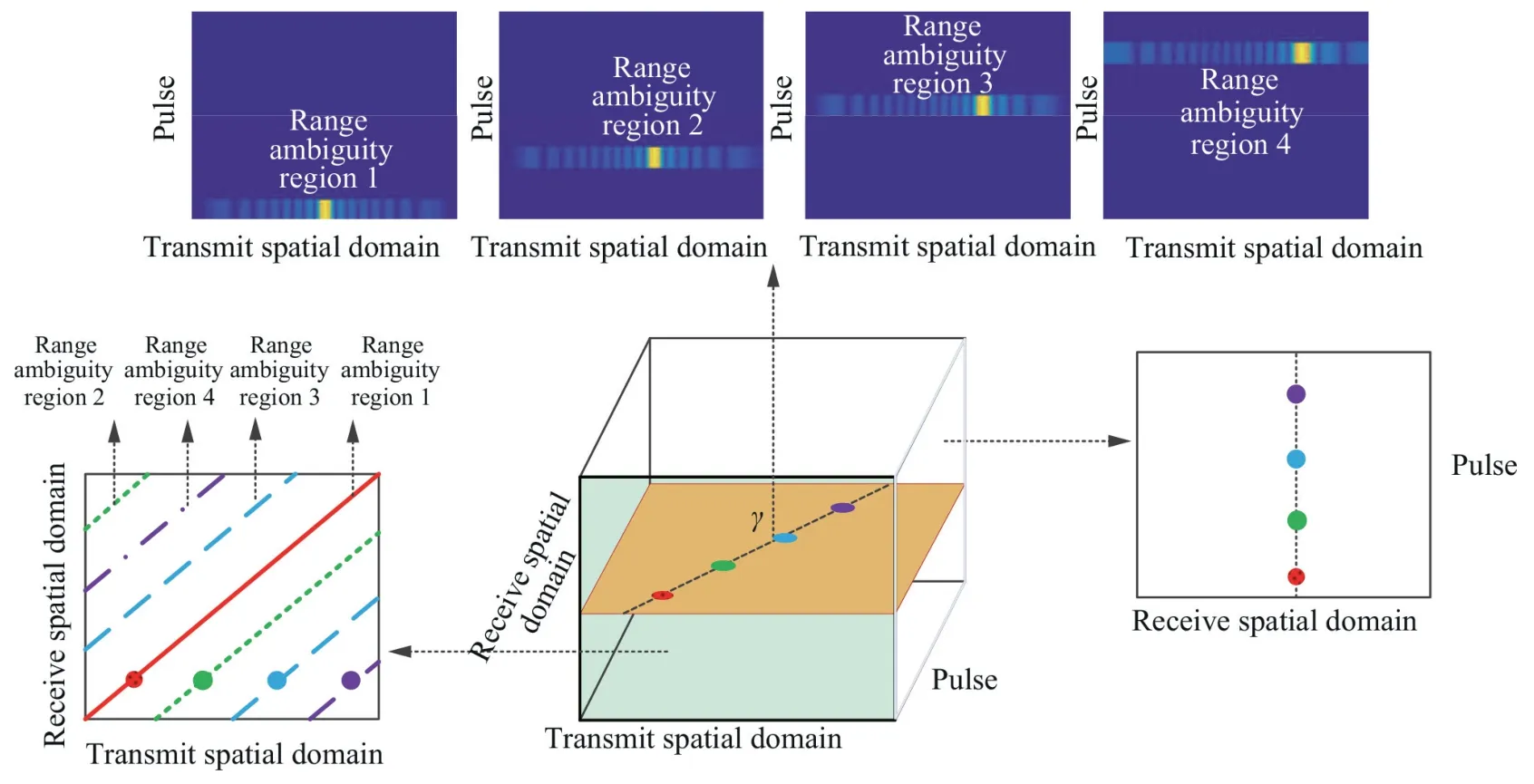
Fig.8 Equivalent beampatterns corresponding to different range ambiguity regions in EPC-MIMO radar.

4.Control of range-dependent beampattern

This section focuses on how to control the range-dependent beampattern in waveform diverse array radars,with emphasis on the properties within the pulses.First,the spatial coverage is analyzed.Then.the methods to decouple the angle-rangetime-dependent transmit beampattern are summarized.Moreover,the control of the joint transmit-receive beampattern is studied.

4.1.Spatial coverage

In this subsection,the coherent FDA with pulse radar system is focused,where the transmit beampattern at a given time instant is studied.As illustrated above,a ‘S’-shaped rangedependent beampattern can be obtained,where the energy is distributed in any direction.Fig.9 analyzes the spatial coverage of the transmit beampattern with different pulse durationTpand frequency increments Δf.It is observed from Fig.9 that the spatial coverage is determined byTpand Δf,where the region of the spatial coverage in transmit beampattern is flexibly controlled by changing the system parameters.In particular,for a fixed Δf,the full spatial coverage from -π to π is achieved whenTp=(see in Fig.9 (a)).However,as shown in Figs.9 (b) and (c),only limited spatial coverage can be achieved whenTp＜Moreover,as shown in Fig.9 (d),for the same pulse duration,the width of the mainlobe in the range domain increases as Δfdecreases.Actually,according to the expression of the transmit beampattern in coherent FDA,for a fixed time instant and angle,the nulls of the beampattern in Eq.(24) are determined according to

Fig.9 Analysis of spatial coverage in FDA with pulse radar system.

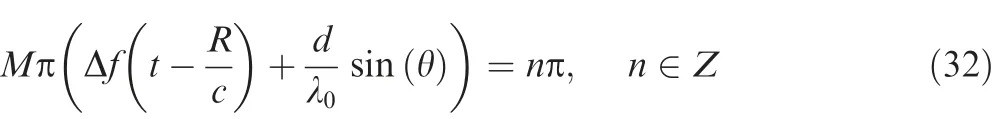
where the width of the mainlobe can be calculated aswhich coincide with the result in Fig.9(d).Similarly,in STCA radar,the spatial coverage can be controlled by designing the time difference Δt.

4.2.Angle-range-decoupled beampattern

Although a range-dependent transmit beampattern is obtained in coherent FDA,the range and angle information are coupled with periodic multiple-maxima in space,141leading to a group of ambiguous angle-range pairs w.r.t.the target.To this end,the selection of frequency offset is essential to steer the beam towards a target with fixed range and angle parameters precisely.61Instead of linearly increased frequencies,methods have been proposed to design the nonuniformly increased frequencies with them-th frequency expressed as

More generally,a focusing beampattern with a minimizedarea has been generated in Ref.66by modelling the beampattern as an ellipse.A vertical ellipse in the joint range-angle domain is shown in Fig.10,where the range and angle axes correspond to the major and minor axes,respectively.66

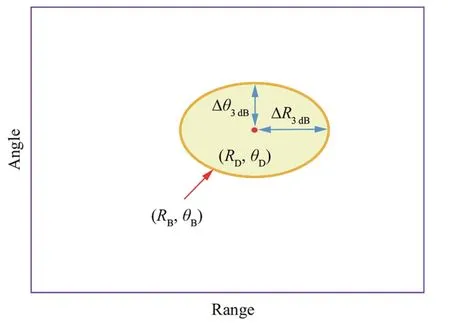
Fig.10 Elliptical beampattern in Ref.[66].

In this regard,a closed form corresponding to the area of the transmit beampattern is given by66

4.3.Time-invariant beampattern

Furthermore,the transmit beampattern of coherent FDA is time-variant,which increases the difficulty in target detection and decreases the received Signal-to-Interference-plus-Noise Ratio (SINR).141Hence,it is of importance to realize a timeinvariant focusing beampattern.In this respect,the time modulation schemes have been introduced into frequency offset control,where the time-varying frequency offsets of them-th element set in Time-Modulated Frequency Offset (TMFO)-FDA,143Time-Modulated Logarithmically increasing Frequency Offset (TMLFO)-FDA67and Time-Modulated Optimized Frequency Offset (TMOFO)-FDA68are respectively expressed as

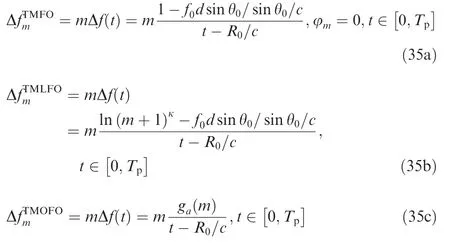
where φmin Eq.(35a) denotes the weighted phase of them-th element,κis a controllable parameter w.r.t.the frequency offset,ga（0）=0 for Δf0（t）=0,andga（n）,n=1,2,···,M-1 is a nonlinear function with nonnegative values,obtained based on waveform optimization.68Fig.11 presents the time-invariant transmit beampatterns using the methods in Refs.67,143.It is shown that the spatial focusing performance is enhanced using the time-modulated increments.However,it is pointed out in Ref.71that a time-invariant focusing beampattern,for some specific spatial positions and time,cannot be obtained once transmitting the pulse signals.Moreover,it is also highlighted in Ref.72that the range is related to the transmit delay instead of the time index within pulse.Hence,the phase difference between the signals w.r.t.them-th element and reference element is independent of the range parameter instead of the range-angle parameters,which is shown as follows:

Fig.11 Time-invariant transmit beampatterns in coherent FDA radar.67,143

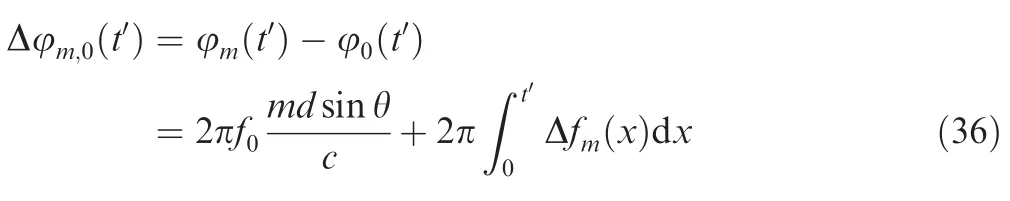
wheret′denotes specific instantaneous time and Δfm（t）is the time-modulated frequency increment in Ref.143.

4.4.Transceive beampattern

Different from the range-angle-time-dependent transmit beampattern in coherent FDA radar,the transceive beampattern of FDA-MIMO radar is range-angle-decoupled and timeinvariant,where there is only one maxima at the position of the target.According to the expressions of the transmit and receive steering vectors,the transmit and receive spatial frequencies are respectively given as

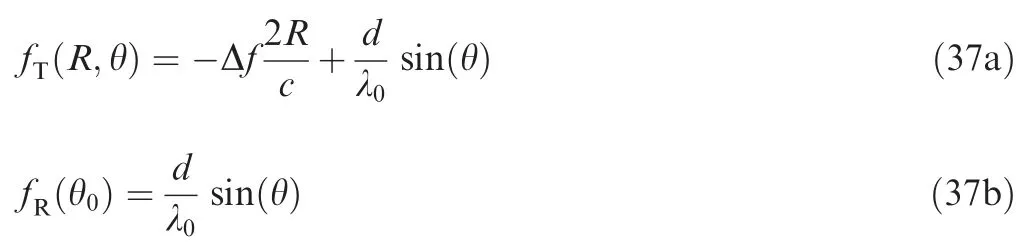
Hence,the 2D transceive beampattern in the range-angle domain is equivalent to the one in the transmit-receive spatial frequency domain.

As the beampattern design is of significant importance to enhance system performance,it is worth investigating the beampattern synthesis for exploiting specific peculiarities of FDA-MIMO radar.In practice,it is desirable to design a beampattern with nulls to handle the interferences from surroundings;however,the interferences will not be exactly located at the nulls,especially in dynamic environments.To solve this problem,in Ref.73,artificial interferences with prescribed powers are assigned within the given rectangular regions in the joint transmit-receive spatial frequency domain in FDA-MIMO radar.In this context,the interference-plusnoise covariance matrix resorting to the Concurrent Null Broadening Control (CNBC) algorithm is constructed as73

where UJ=[u1,u2,···,uL] is anMN×Lmatrix with ulbeing thel-th(l=1,2,···,L)null steering vector,R0=,and ΣJindicates the Jammer-to-Noise Ratio (JNR) matrix.Then,the closed-form expressions of artificial interference powers are obtained according to the presumed responses,where the power of thel-th interference is obtained according toP（ul|u0）=ξlwith ξlbeing a predefined depth at ul.Hence,a trough-like transceive beampattern can be formed,where rectangular null regions are broadened.

To further control the mainlobe region of the transceive beampattern,the rec-preset PBPS technique was proposed in Ref.116by controlling the rectangular regions directly.In this respect,based on the Weight vector ORthogonal Decomposition (WORD) algorithm,144the weight vector corresponding to thel-th iteration is updated as

Moreover,as the WORD algorithm can only control a single response,to circumvent these deficiencies and control multiple responses simultaneously,the oblique projection was utilized in Ref.75,where the concurrent MRCOP is developed to adjustKpoints from their corresponding regions concurrently.In this respect,a filtering matrixis constructed as

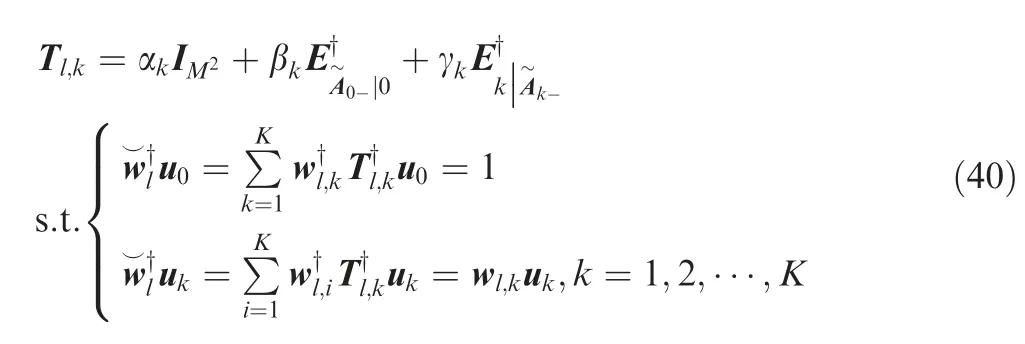
where αk∈R1,βk∈R1,and γk∈R1are the coefficients which can be determined according to the constraint at the presumed position.Note that Tl,kpasses ul,kand blocks the components from other regions,and the final weight vector is obtained by filtering sub-weight vectors fromKregions aswith wl,k∈being the weight vector which controls the response of thek-th region in thel-th iteration.In Fig.13(b),measured results are provided to evaluate the effectiveness of the proposed methods,where the antenna measurement is carried out.Figure inspirations in Fig.13 (b)highlight that,although the response cannot be as desired due to system errors with measured data,the proposed CMRCOP method is effective in forming a range-angledependent transceive beampattern with a desired shape,where two rectangular null regions and a flat-top mainlobe can be obtained.Note that the data-independent beamformers are focused to control the responses with the above beampattern synthesis methods,where the adaptive array theory is applied to the data-independent beamforming.73,75,116

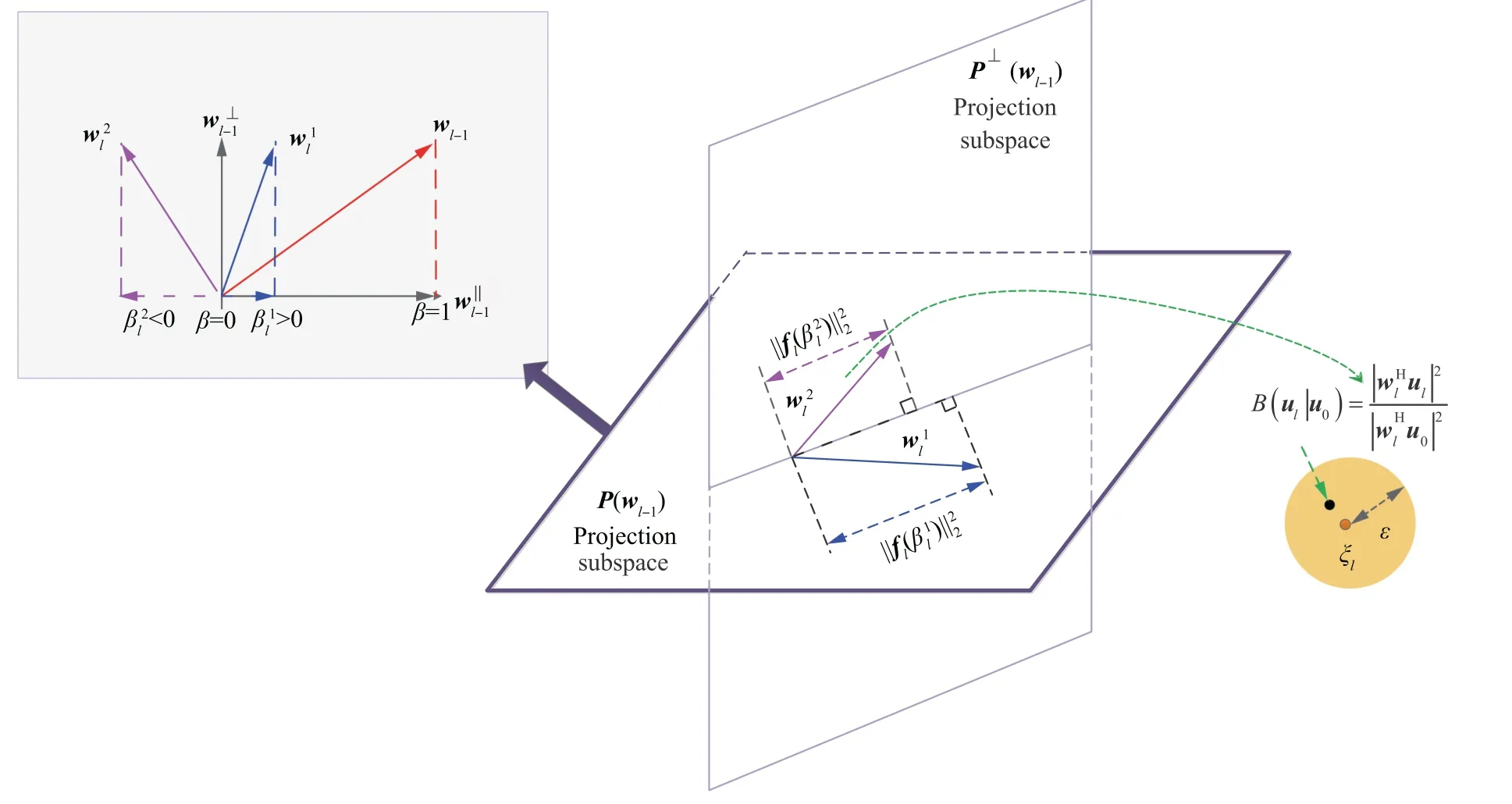
Fig.12 Illustration of WORD algorithm.

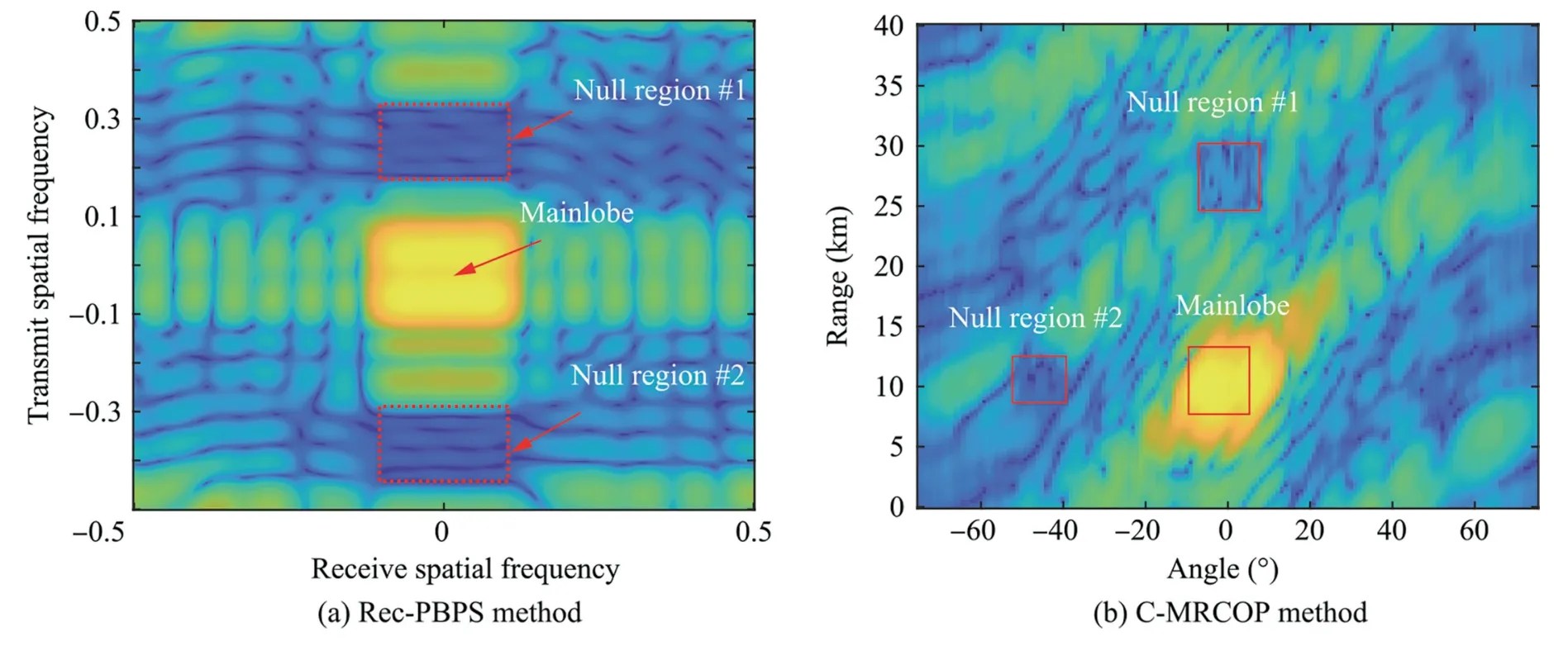
Fig.13 Transceive beampattern synthesis in FDA-MIMO radar.

5.Utilization of range-dependent beampattern

Capitalizing the range-dependent beampattern,especially the ambiguous range across different transmit pulses,a multitude of applications,ranging from jammer suppression to SAR imaging,can benefit from the waveform diverse array radars.This section summarizes the applications of the rangedependent beampattern in waveform diverse array radars,including the adaptive target detection,joint parameters estimation,range-ambiguous clutter suppression,mainlobe deceptive jammer suppression and HRWS SAR imaging.

5.1.Adaptive target detection

The problem of target detection in FDA-MIMO radar was studied by ignoring the clutter in Ref.76,and besides,the target range and interference covariance matrix are assumed known.Moreover,a conic model for the desired target signal has been considered in Refs.77–79with known interferenceplus-noise covariance matrix.However,the signal models above are unrealistic,where both the interference-plus-noise covariance matrix and some parameters of the target are usually unknown in practice.In this respect,the adaptive detection exploiting the GLRT criterion in FDA-MIMO radar was investigated,80where detection architectures were developed according to the Maximum Likelihood (ML) estimation of the parameters.

Considering the Gaussian noise,denote zk∈CMN,k=1,2,···,K≥MNand z ∈CMNas a set of secondary data and the data collected from the Cell Under Test (CUT),respectively,and a binary hypothesis test is formulated to illustrate the detection problem80as

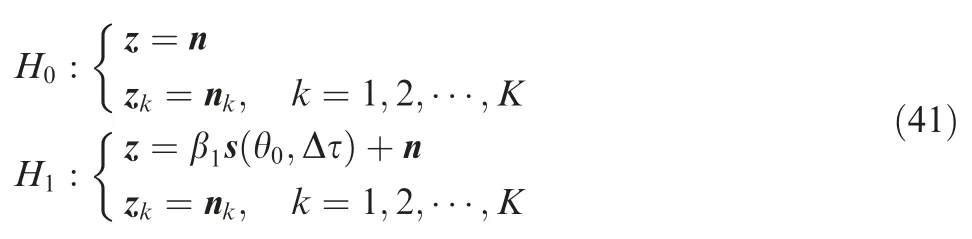
where n and nkare modeled as zero-mean Gaussian noise,i.e.,n～CN（0,M）and nk～CN（0,M）with M ∈CMN×MNbeing the interference-plus-noise covariance matrix.The GLRbased architectures decision statistic,related to the incremental range Δτ,can be expressed as

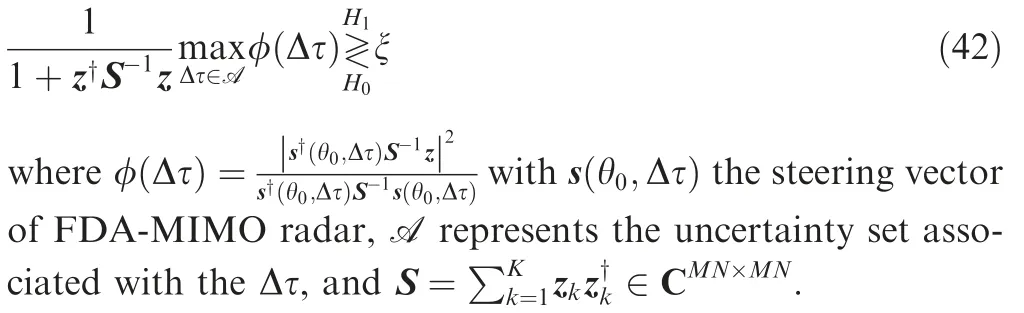
To solve the problem,three approaches are considered in Ref.80.Firstly,by utilizing the relationship between linear matrix inequalities and nonnegative trigonometric polynomial inequalities,an SDP-based optimal detector is developed aswithobtained from the convex SDP optimization problem.145Then,to reduce the computational burden,two sub-optimal approaches are designed to approximate the optimal search.The finite grid search approach is developed,where the range interval within the CUT is discretized in a finite number of points.Then,the improved approach with a Newton-based refinement procedure is developed to avoid excessive straddle loss by utilizing the grid search method.

Fig.14 provides the performance of target detection w.r.t.detection probabilityPdversus input SINR for different frequency increments Δfand numbers of grid pointsQ.It can be seen from all figures that the benchmark detectors produce the best results,and the Newton-based refinement procedures have better performance compared with the grid search counterparts.By comparing Figs.14(a)and(b),it is observed that the lower the Δf,the smaller the performance loss.Moreover,comparisons among different numbers of grid points are given in Fig.14 (c) and (d).It is shown that both the performance corresponding to the Newton-based procedure and grid search approaches (withQ＞1) are close to the respective benchmarks;however,the performance gap between the Newtonbased and the grid search methods is lower with largerQ.

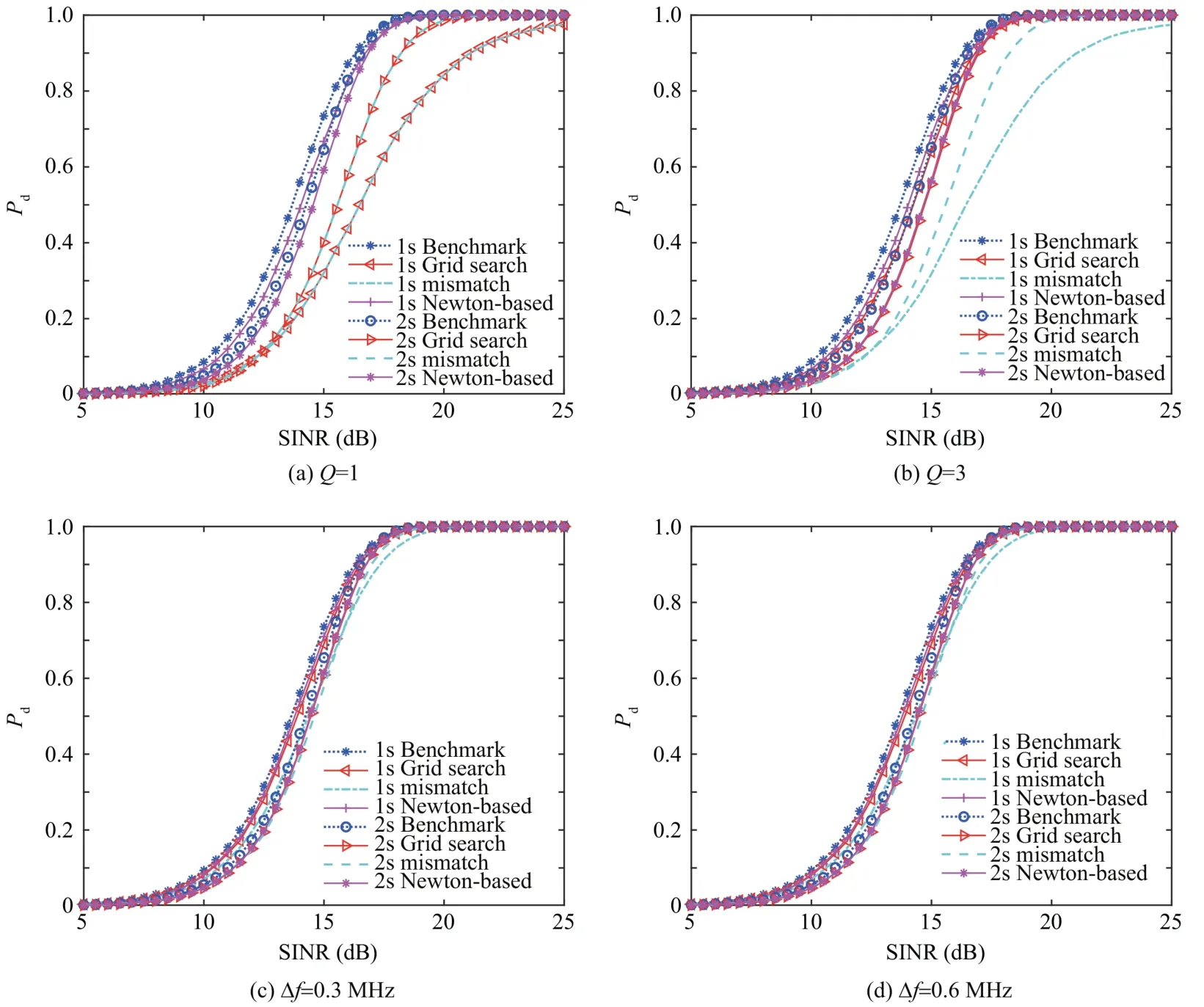
Fig.14 Pd versus input SINR.80

5.2.Joint parameters estimation

Actually,after matched filtering in the FDA-MIMO radar,by stacking the columns of the received data into a vector form and obtaining the noise-plus-interference covariance matrix,the subspace algorithms,such as the MUSIC algorithm,the Capon,and the ESPRIT,can be performed.In Ref.86,the targets are localized via MUSIC algorithm as the peak:

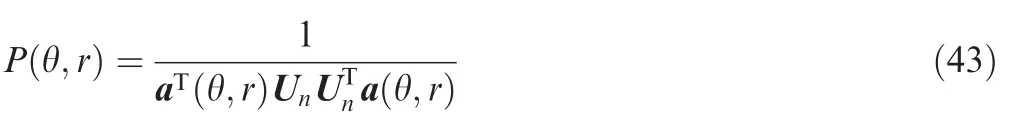
where Undenotes the subspace of the noise.Similarly,the ML estimates of the range and angle can be determined by maximizingwith the weight vector w0obtained with the covariance matrix according to the Capon.91Moreover,the two-stage ESPRIT algorithm was proposed in Ref.90,where the receive array is divided into two subarrays to obtain the signal subspaces.

However,the computational cost is high via a 2D search,and the performance of subspace-based algorithms degrades due to lack of sufficient snapshots.In Ref.91,the estimation problem is formulated using a single snapshot.Firstly,an iterative algorithm is designed based on the Coordinate Descent(CD) algorithm via a sequence of One-Dimensional (1D)searches to find the maximizer,which alternates the optimization over one variable while keeping the other fixed.91To further reduce the computation load of the 1D searches,two kinds of approximated methods based on the monopulse procedure are considered exploiting real and complex slope/bias correction values.In this context,the vectors h containing the range and angle parameters to be estimated by utilizing the Adaptive Monopulse Procedure (AMP) and the Adaptive Generalized Monopulse Procedure with Complex Correction(AGMP-CC) are respectively given by91

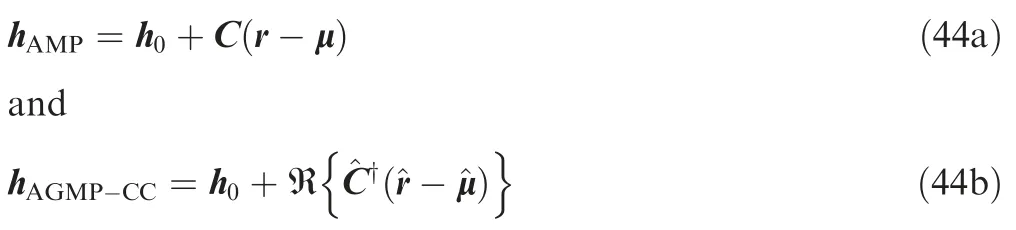
where h0denotes the nominal values of the unknown parameters containing the angle and incremental range;C and ^C denote the real and complex slope correction matrices,respectively;μ and ^μ represent the real and complex bias correction vectors,respectively;r and ^r refer to the real and complex monopulse ratio vectors,respectively.

Moreover,the CRBs for angle and range parameters are respectively calculated as85,91

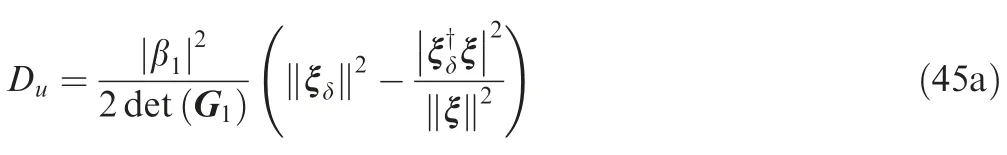
where the weight vector ξ is obtained with the covariance matrix Q and the data snapshot s,and the derivatives of ξ are obtained as ξh=withh∈｛u,δ ｝.Considering the CRBs for angle and range as the performance benchmarks,the estimation performance in the background of white Gaussian interference is illustrated in Fig.15.91Inspection of Figs.15 (a) and (b) highlights that the Root Mean Square Errors (RMSEs) for all the estimators are lower with the higher SINR.Besides,some of the estimators approximate the CRB benchmark with a sufficiently high SINR.91The bias and variance ellipses of the estimators are displayed in Figs.15 (c) with 15 points and SINR=20 dB,where the analysis of bias and variance confirms that all the monopulse estimators experience a bias in both angle and range domains.91

Fig.15 Comparison of estimation performance assuming white noise.91

5.3.Range-ambiguous clutter suppression

In FDA-MIMO radar,the DOFs are 3D,i.e.,the transmit,receive and pulse dimensions owing to the ambiguous rangedependent beampattern,which can be applied in rangeambiguous clutter suppression.101,103–107A Secondary Range Dependence Compensation (SRDC) method was proposed to separate the range ambiguous clutter in the spatial frequency domain,101where the compensating vector can be formulated by Ref.101

Moreover,to reduce the dimension of the processor rangeangle-Doppler processing,an adaptive range-angle-Doppler processing method based on 3D Localization (3DL) was devised by using multiple beams in the transmit,receive,and Doppler domains,104which can be expressed as

5.4.Mainlobe deceptive jammer suppression

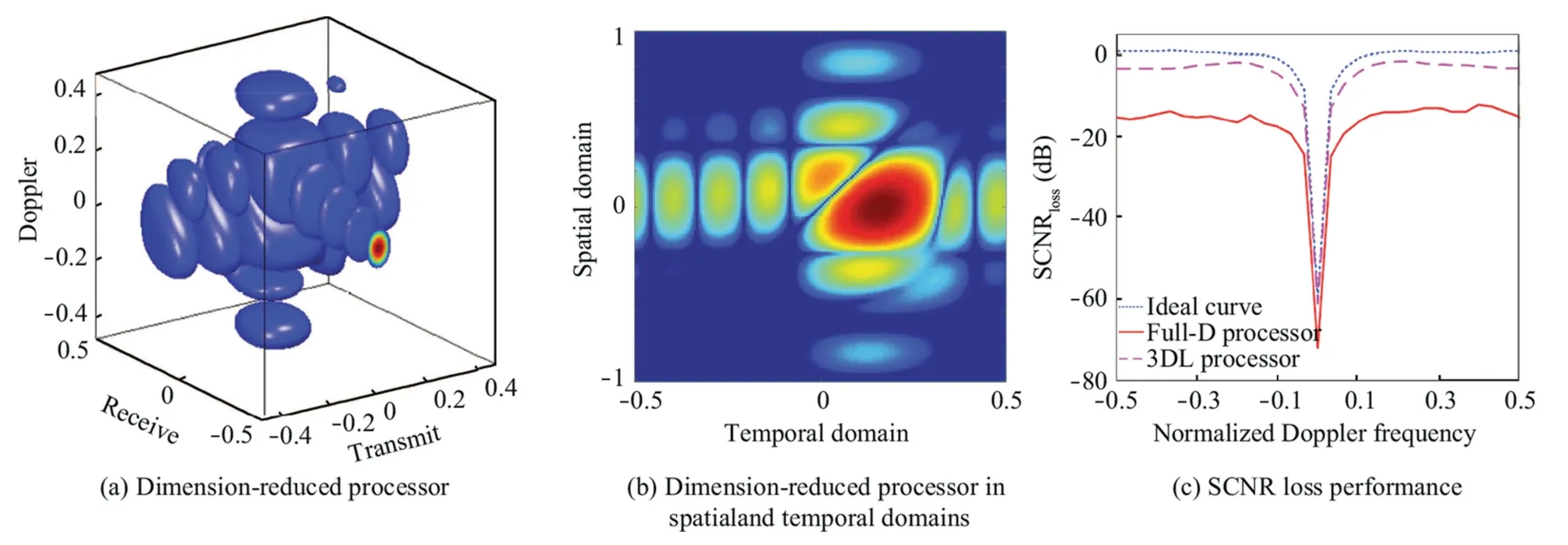
Fig.16 Result of clutter suppression in FDA-MIMO radar.104

The controllable DOFs have been introduced by transmit modulation in waveform diverse array radars,providing an effective way to suppress the mainlobe deceptive jammers.Consider that,the transmitted waveforms of the radar system are intercepted by the False Target Generator (FTG) andQpseudo-randomly distributed false targets are generated after time modulation to deceive the victim radar.115Hence,the actual range of the false target is larger than that of the true target,115leading to a difference between the true and the false targets in the transmit spatial frequency domain Ref.85.Note that the condition for jammer suppression in waveform diverse array radars is that the false targets are generated after relatively large time delays,115,116and they lag at least one pulse behind the true target.115,116Moreover,as the jammer suppression is performed in the searching stage,a priori knowledge of the target,i.e.,the index of the delayed pulses,is assumed known.115

Given a specific frequency increment Δfor the coding coefficient γ,the transmit spatial frequency is related to the delayed pulses numberp.Hence,the true and false targets are distinguishable in the transmit spatial frequency domain as they correspond to different transmit pulses.Hence,the jammers are suppressed by nulling using the joint transmit-receive beamforming.In this context,the existing methods to suppress the mainlobe deceptive jammers with waveform diverse array radars can be divided into three categories,including the adaptive beamformer based methods,108,110,111,113,114the subspace projection-based methods109,112and the beampattern synthesis-based methods.115–117

5.4.1.Adaptive beamformer based jammer suppression methods

To suppress the mainlobe deceptive jammers,the received signals are processed via a joint data-dependent 2D beamformer by resorting to the Minimum Variance Distortionless Response (MVDR) beamformer,which is mathematically expressed as114

where Rj+nis the jammer-plus-noise covariance matrix,u（R0,θ0）is the transceive steering vector of the true target,and w=represents the optimal weight vector.As a result,the jammers are suppressed because of the range mismatch.However,the i.i.d.condition for the training data cannot be satisfied due to the random time-delay in FTG.114Therefore,in order to estimate the jammer-plus-noise covariance matrix,a robust Nonhomogeneous Sample Detection(NSD) method is proposed by selecting the nonhomogeneous samples (including the jammers and the signal) and rejecting the samples including the signal.114Fig.17 demonstrates performance of jammer suppression with the NSD method.The response of the transmit-receive adaptive beamformer is shown in Fig.17(a),where a maximum is achieved in the position of the target.It is observed in Figs.17(b)and(c)that the performance loss is considerable due to self-cancellation using the adaptive NSD method,In contrast,the mainlobe deceptive jammers can be effectively suppressed with the robust NSD method,and the output SINR performance is high,which is close to the upper bound.

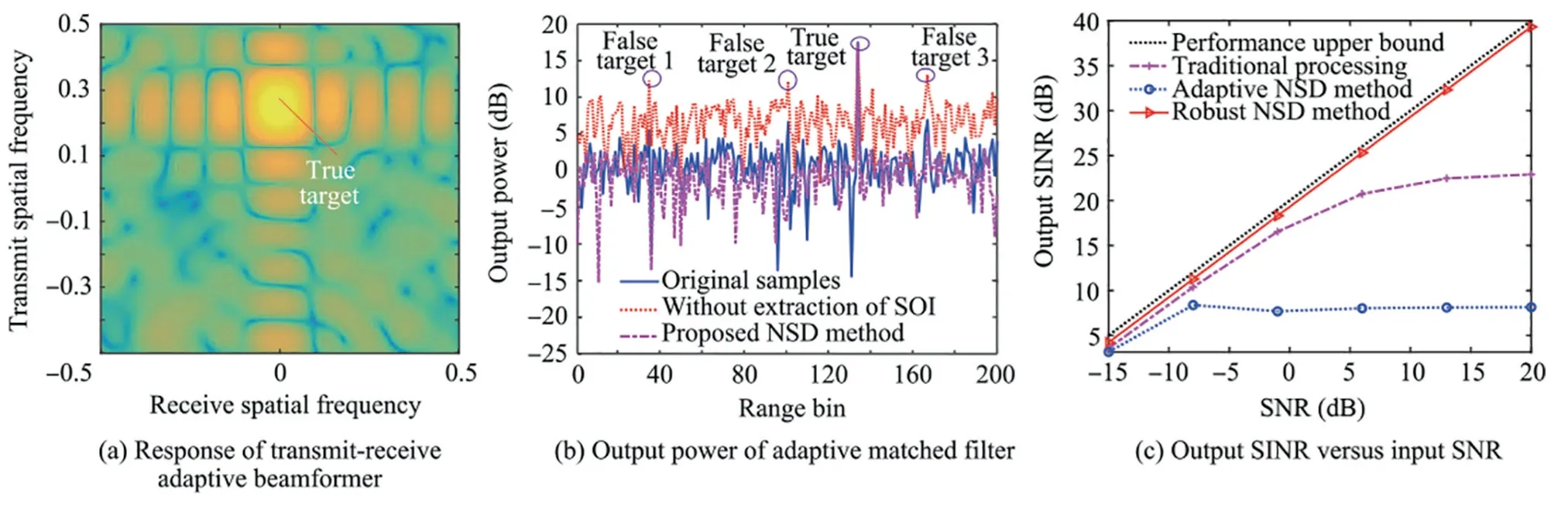
Fig.17 Results of jammer suppression in FDA-MIMO radar with robust NSD method.

5.4.2.Subspace projection based jammer suppression methods

Considering that the adaptive beamformer-based methods depend on the accuracy of a priori knowledge,some subspace projection based methods have been carried out to suppress the jammers.109,112

Moreover,the ‘‘Go Decomposition” (GoDec) method via alternating minimization was devised In Ref.112to suppress false targets,where the mixed jamming signals,including the barrage jamming and burst jamming,are considered.For the total data snapshots in the 2D time domain Y=Xs+Xi+Xe+Xn,because both the signal data Xsand the jamming data Xihave the property of low rank,and the burst noise data Xehas the sparsity property,Y is decomposed into three independent matrices,i.e.,Ls,Liand Sewith Lsbeing the estimate of Xs.112Hence,in order to find the matrix Lsfrom the corrupted measurement Y,the approximate decomposition problem can be formulated by minimizing the decomposition error with Frobenius norm112:

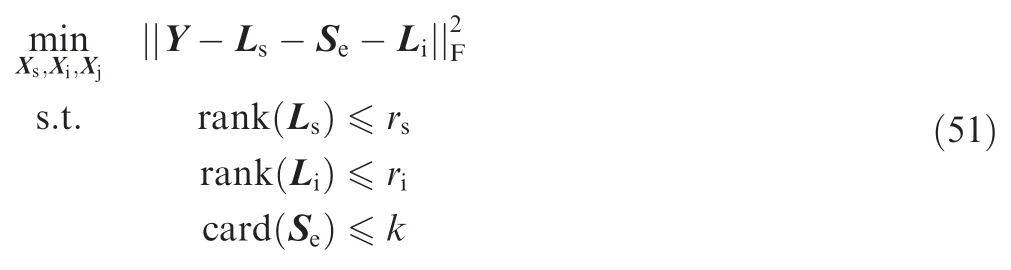
wherersandridenote the rank of matrices Lsand Li,respectively,andkis the cardinality of the matrix Se.Hence,by utilizing the GoDec method to update Ls,Liand Se,the estimate of Lscan be finally obtained,and the false targets are effectively suppressed.

5.4.3.Beampattern synthesis based jammer suppression methods

The data-independent beamforming can be applied in jammer suppression in waveform diverse array radars,where the false targets are suppressed by nulling at the equivalent transmit beampattern.Fig.18115,116demonstrates the distributions of the true and false targets in the joint transmit-receive spatial frequency domain for both the FDA-MIMO radar and EPCMIMO radar,where the true target is located on the diagonal line because of the identical transmit and receive spatial frequencies for both cases.However,the false target withpdelayed pulses is located with an offset by -and -γpalong the transmit spatial frequency domain in FDA-MIMO radar and EPC-MIMO radar,respectively.Hence,according to the expression of the transmit beampattern,theq-th false target is exactly located at the null of the beampattern when the frequency increment and the coding coefficient satisfy

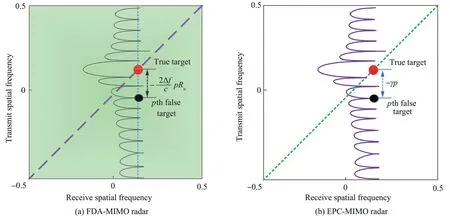
Fig.18 Positions of true and false targets in joint transmit-receive spatial frequency domain of waveform diverse radars.115,116

Actually,the transmit spatial frequency difference between the true and theq-th false target can be expressed as116

wherez=int（Δf/fr）is the integer part,which can be ignored because of 2π periodicity of the phase difference,115andudenotes the decimal part,in which∉Z+must be satisfied to guarantee effective discrimination of the true and false targets.115

As illustrated above,the principle of jammer suppression via data-independent beamforming is nulling the false targets by designing an appropriate frequency increment or a coding coefficient.Moreover,it is observed in Fig.19 (a) that the EPC-MIMO scheme can discriminate aliased mainlobe echoes corresponding to the false targets from different range regions because the mainlobes of their equivalent transmit beampatterns have different directions.116,117Besides,by designing,the mainlobes of the false targets are located exactly at the nulls of the beampattern.Hence,the echo of the true target can be extracted,and those from other undesired ambiguous range regions are suppressed,which can be seen in Fig.19(b).Furthermore,as shown in Fig.19 (c),taking the false target 1 (with one delayed pulse) as an example,by choosing different γ,the mainlobes of the equivalent transmit beampatterns w.r.t.the false target 1 correspond to different nulls.116

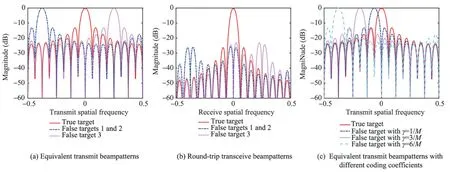
Fig.19 Beampatterns in EPC-MIMO radar for jammer suppression.116,117

However,the above methods are invalid when considering the deviations from their presumed positions in the beampattern in practice.In other words,the jammer suppression performance degrades when deviations exist for both the presumed nulls of the false targets,and the mainlobe of the true target.116Such mismatch could occurs due to quantization errors,frequency increment error,and angle measurements.115In addition,the range of the moving target corresponding to different transmit pulses varies,leading to a deviation between the actual transmit spatial frequency and its presumed value.Moreover,the array amplitude and phase errors also affect the position and depth of the nulls.Hence,to strengthen the robustness of jammer suppression,it is desired to design the beampattern with a flat-top mainlobe,broadened nulls,and low sidelobes via the pattern synthesis methods to mitigate possible angle/range mismatches.116

In Ref.115,a Preset Broadened Nulling BeamFormer(PBNBF) algorithm was proposed,where the nulls are broadened by imposing artificial interferences with appropriate powers around the null regions.Fig.20(a)displays the broadened notches in the transmit-receive 2D beampattern with a presumed null depth.115The output SINR curve versus different quantization errors is displayed in Fig.20 (b),where the conventional data-independent beamformer is sensitive to the quantization error.However,with the broadened nulls,the output SINR is steady with the varying mismatch.Moreover,as shown in Fig.20(c),the PBPS algorithms are developed In Ref.116,and it shows effective suppression performance w.r.t.the output of the matched filtering when Direction-Of-Arrival (DOA) mismatch exists.

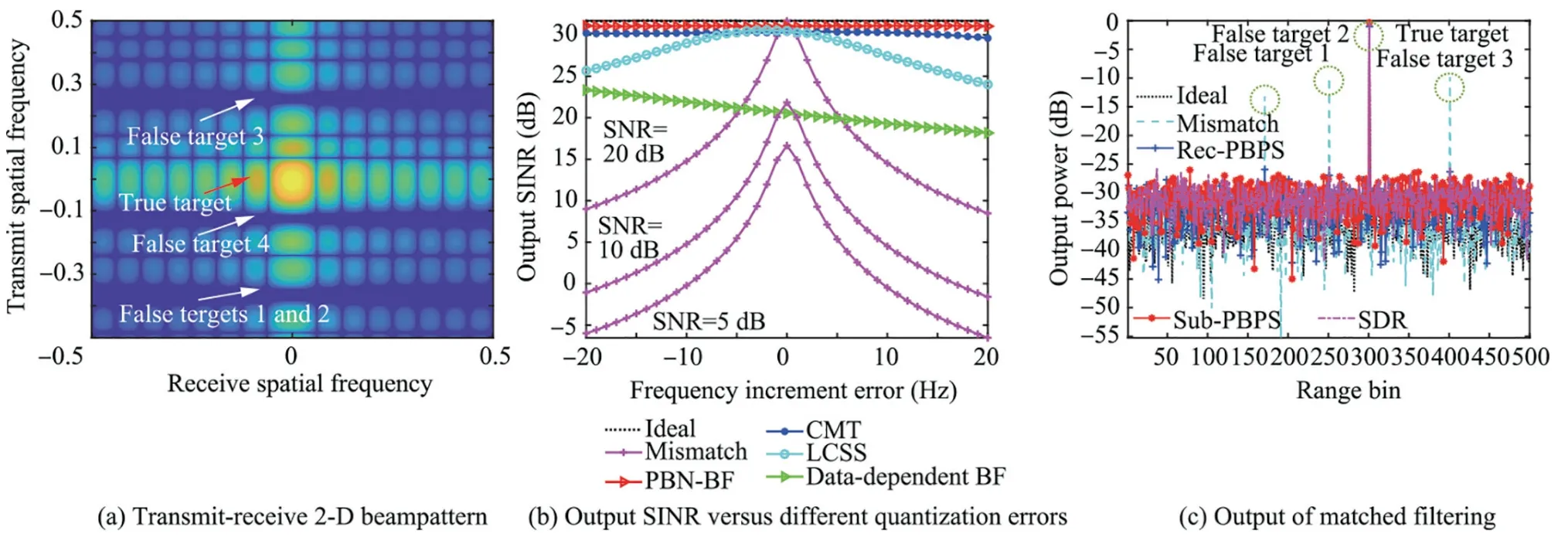
Fig.20 Robust jammer suppression results with beampattern synthesis in waveform diverse array radars.115

5.5.HRWS SAR imaging

The ambiguity commonly exists for range and azimuth domains during the process to realize HRWS SAR imaging,where there is a contradiction between the high azimuth resolution and wide swath.146,147Although it is easier to resolve the azimuth ambiguity rather than the range ambiguity,the requirement for wider swath width to realize HRWS imaging makes it significant to resolve the range ambiguity.Besides,the concept of MIMO-SAR has been proposed In Ref.28,where the concept of short term shift orthogonal waveforms is introduced,and the capabilities of imaging can be enhanced.However,in traditional MIMO-SAR system,the range ambiguities cannot be discriminated,and the directions of the mainlobes corresponding to their transmit beampatterns are the same for all ambiguous range regions.44To overcome the problem of range ambiguity,the FDA is employed in SAR system,118–123,125where range-dependent beampattern makes it possible to overcome the range ambiguity unaliasing in the spaial domain.Actually,as discussed above,by utilizing the extra range DOFs,the waveform diverse array radars can distinguish the echoes from different range ambiguity regions to achieve HRWS imaging.44,122,148Actually,because the spatial frequency is range-independent with traditional MIMO system,the echoes from different range ambiguity regions are overlapped in the spatial frequency domain Ref.116.However,as shown in Fig.21,the range ambiguous echoes spread in the spatial frequency domain,and they can be distinguished because the corresponding equivalent pointing directions are different.

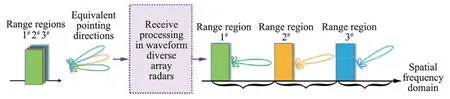
Fig.21 Range-ambiguous echoes separation in transmit spatial frequency domain.

In Ref.122,the procedure of Range Dependence Compensation(RDC)is performed with the received data,and then,the range ambiguous echoes are discriminated after the matched filtering and receive beamforming in FDA-SAR.Then,the traditional SAR imaging procedure is carried out to the reconstructed unambiguous echo,which follows the HRWS imaging results of the full swath.Specifically,according to,122the frequency increments should be well designed to avoid the spectrum overlapping of different range regions.122Besides,the minimum distance between two adjacent range regions～uis supposed to be as much as possible to guarantee the effective separation.What’s more,allNarange regions need to share the whole spatial frequency [- 0.5,0.5].Hence,the selection of the optimal frequency increment is discussed as follows:

Moreover,the MIMO-SAR with Space-Pulse Phase Coding(SPPC)was proposed In Ref.44to achieve HRWS imaging,where the coding phases on transmit channels for each transmitted pulse are carried out.Particularly,the coding phase of them-th transmit channel at the slow timetkis expressed as44

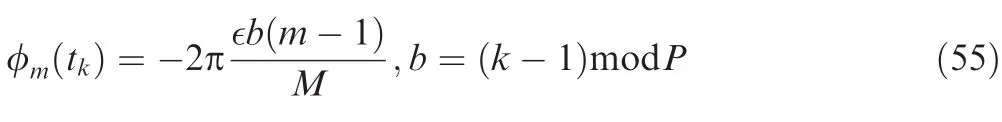
where ∈∈R is an phase gradient factor,by which the distance between adjacent range ambiguity regions can be controlled,andPdenotes the number of total ambiguous range regions.In Ref.44,three ambiguous range regions are assumed,where Fig.22 (a) illustrates the coding phases of the echoes associated with the pulses transmitted at them-th element.44In order to obtain the image of the first range region,the decoding w.r.t.the slow time is performed to avoid the range walk by removing the phases that result from the coding,that is,shifting the equivalent beam-pointing to 0o.44Moreover,the residual coding phases after decoding the echoes corresponding to the first region are shown in Fig.22 (b),where the pointing direction corresponding to the first range region is at 0ow.r.t.the slow time,and the pointing directions corresponding to other range regions are different.44

Fig.22 Phases of echoes corresponding to transmitted pulses of the m-th channel.44

Fig.23 (a) displays a complex scene with multiple distributed targets to verify the performance of the HRWS imaging,where the image is aliased with three range ambiguity regions in a traditional SAR.44The unambiguous imaging results for the three range regions with the SPPC scheme after decoding are shown in Figs.23 (b)-(d),respectively.It can be observed that the scene image for each region is cleaned,and the undesired images corresponding to other ambiguous regions are suppressed.44

Fig.23 Imaging in a complex scene.44

Furthermore,considering the requirement for simultaneous image of multiple targets within a wide spatial angle region in Inverse SAR(ISAR)system,an approach to separate multiple targets was proposed in Ref.148by transmitting the time-delay LFM signal and utilizing the time-delay receive scheme.As shown in Fig.24(a),the LFM signal is transmitted by a single element with a time delayTd,which is regarded as the multirate sampling.In Fig.24 (b),a time-delay receive array withMelements is considered.Owing to the range-angledependent beampattern in time-delay receive array,the echoes for different targets can be discriminated in the equivalent spatial frequency domain.Then,the echo with mixed multiple targets is resolved into several single-target parts by performing the receive beamforming,where the weight vector is designed according to the desired target.In the sequel,the wellfocused ISAR imaging of each target is achieved with the traditional imaging method,i.e.,the range alignment and phase compensation.148

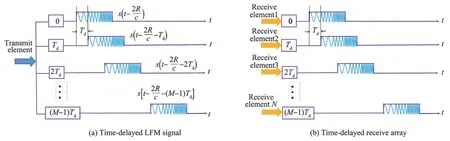
Fig.24 Geometry of time-delay scheme for ISAR imaging.

6.Experimental systems for waveform diverse array radars

In addition to the theoretical research of the waveform diverse array radars,the development of the corresponding experimental systems is also significant.In 2009,the experiments have been carried out to validate the theory and simulation of the FDA,including both bench tests and radiated field measurements,31where the developed system and the corresponding results are presented in Fig.25.The transmit antenna,with the carrier frequency equal to 3 GHz,is constructed with 15 microstrip patch radiators,of which 3 elements in each column are utilized to form a single subarray.31Hence,5 spatial channels can be obtained.The full transmit array mounted on the backplane and the 5 spatial channels of the transmitter mounted in place are shown in Fig.25(a)and(b),respectively.Two receive channels were developed,where a fully constructed channel is shown in Fig.25 (c).Hence,the rangeangle diagram for the experimental setup is shown in Fig.25(d) with=0.45 and Δf=2.5 MHz.The measured beampattern shows good agreement with the theoretical analysis on the‘S’-shaped range-angle-dependent characteristics.

Fig.25 Experiments of FDA carried out by Antonik et al.31.

In the same year,the Phase Locked Loop (PLL) frequency synthesis technique was introduced In Ref.149as an effective approach to generate the frequency diverse signals.The system with a compact integer-N of PLL frequency synthesizer for FDA is given in Fig.26 (a),where the 2-layer circuit is presented in Fig.26 (b).In this design,the 4 hex rotary switches are employed to set the correct control bit to‘N’and‘A’counter.Hence,by changing the positions of 4 rotary switches,the frequency synthesizer gives outputs of different frequencies.

The implementation of the FDA system with Continuous Waveform (CW) is performed In Refs.150,151,where the designed hardware,waveform generators and measurement devices are explained.As shown in Fig.27,to test the validity of the theoretical analysis on the range-angle-dependent beampattern,the test setup is implemented in the anechoic chamber.151Moreover,the LFMCW source is connected to a transmit antenna with a wide band,and then,the waveform is received by designed array,whose output is detected and compared to the trigger signals from the waveform generator.151

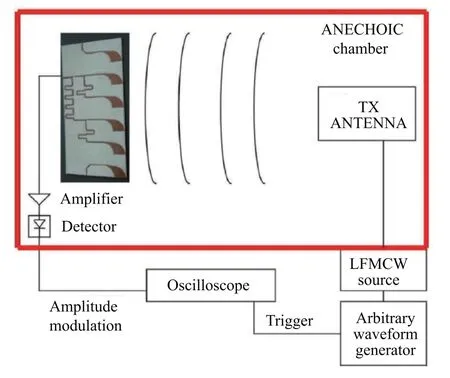
Fig.27 Test setup of FDA with LFMCW implemented by Demir et al.151.

In 2017,the FDA multi-channel signal source and antenna were developed by Wang et al.139,where the multi-channel signal frequency synthesizer and the transmitting antenna are displayed in Figs.28 (a) and (b),respectively.

Fig.28 FDA radar frequency synthesizer,antenna and software designed by Wang et al.139.

Furthermore,the waveform diverse array radar system,including the antenna and Radio Frequency(RF)components,signal processor,data memory,display and control subsystem,has been developed by our team since 2017.The antenna radiation array is presented in Fig.29 (a),which consists of 16 groups of subarrays with 1×8 waveguide slot antenna for each.Fig.29 (b) displays the RF components,including 17 groups of frequency conversion components (with 16 groups of digital T/R components,1 group of receive calibration components and 1 for the transmit calibration),1 group of calibration network,frequency source and local oscillator network,control motherboard,power supply and control system.A signal processor,including a timing control board,a 16-channel signal transmitting board and a receiving board is demonstrated in Fig.29 (c).Besides,the display and control subsystem is used to issue commands,switch working modes,monitor RF components,and display target information.The preliminary field test and experiments have been implemented to verify the effectiveness in jammer suppession and estimation,which is shown in Fig.30.Moreover,it can be observed that the experimental results in Fig.31 are consistent with the theoretical analysis that,in traditional phased array and MIMO radars,the mainlobe deceptive jammers cannot be suppressed (see Figs.31 (a) and (b)).However,the jammer can be effectively suppressed with the developed waveform diverse array radar system,which is shown in Fig.31 (d).

Fig.29 Experimental results with waveform diverse array radar system.

Fig.30 Preliminary test and experiments with the developed waveform diverse array radar system.

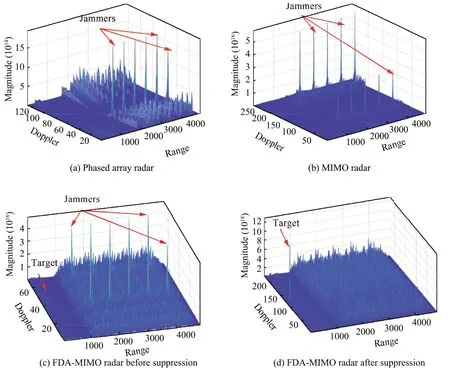
Fig.31 Experimental results for jammer suppression in joint Doppler-range domain.

7.Conclusions and future work

7.1.Conclusions

Waveform diverse array radars,including the FDA,STCA,and EPC,are novel radar frameworks that have sparked intense interest from the signal processing community recently owing to the extra DOFs in the range-dependent beampattern.This paper has provided an extensive investigation on the control and utilization of the range-dependent beampattern with waveform diverse array radars.At the starting point,formulations of the three waveform diverse array radar frameworks have been illustrated by introducing frequency/time/phase modulations across the transmit array.Besides,the rangedependent beampatterns,including the transmit beampattern and the joint transmit-receive beampatterns have been studied,as well as some signal processing methods in the receiver.

Actually,the beampattern within the pulse is a function of range,angle and time,especially in coherent FDA radar,while the beampattern across different pulses is dependent on the ambiguous range,which can be utilized to achieve the range ambiguity.Then,aimed at the range-angle-time-dependent beampattern within each pulse,this paper has investigated the methods to control the range-dependent beampattern in waveform diverse array radars with emphasis on the spatial coverage,angel-range-focusing and time-invariant properties,as well as the synthesis on the joint transmit-receive beampattern.Furthermore,as for the applications of ambiguous rangedependent beampattern between pulses,it is expected to have a profound impact on radar applications,particularly in light of resolving the range ambiguity,which can be utilized in parameter estimation,range-ambiguous clutter suppression,the mainlobe deceptive jammer suppression,as well as HRWS SAR imaging.

7.2.Future work

Despite our best efforts,other salient features w.r.t.the rangedependent beampattern in waveform diverse array radars may be omitted or insufficiently elaborated.Hopefully,however,this paper serves as an adequate starting point for further,deeper investigations into the waveform diverse array radars.Some potential future work is listed as follows:

(1) Considering the fact that it is necessary to separate the transmitted waveforms at the receiver to extract the controllable range DOFs,however,the cross-correlation of multi-channel waveforms will affect the performance of the system in practice.Because,practically,the mutual orthogonality for all Doppler and delay pairs is not realistic,and it poses a theoretical problem of designing and optimizing the orthogonal waveforms,it is necessary to carry out some advanced waveform design techniques based on innovative nonconvex optimization problem tools combined with system constraints as well as their comprehensive performance assessment.

(2) The existing applications of the waveform diverse radars to parameter estimation,detection,and jammer suppression are mainly focused on a single target.However,the practical scene,such as the coherent sources and multipath,calls for investigation on multiple targets,where the problem of parameter identifiability and estimation accuracy are also involved.It is thus worth investigating the detection of multiple targets waveform diverse radars.

(3) Actually,in the complex electrometric environment,it has become a trend to learn about and sense the radar environment,and the cognitive ability has become a key factor in the future electronic countermeasures.Particularly,in actual battlefield environment,the types of jammers should be recognized adaptively and anti-jamming strategies should be taken accordingly.In this respect,it requires the hybrid cognitive methods for improved performance resorting to the neural networks and deep learning algorithms.Moreover,because the cognitive properties have extensively increased the computational complexities,optimal array signal processing algorithms with efficiency and lower computational load are supposed to be investigated.

(4) Although the experimental systems for FDA have been achieved,the design technology of the waveform diverse array radars should be extended.As the STCA is a special MIMO radar,it is easier to transmit the identical waveform with time shifts instead of generating the orthogonal multichannel waveforms.Moreover,as the performance of jammer/clutter suppression degardes with the presence of system errors,it is necessary to perform the error decoupling measurements.

(5) There are still extensive demands for waveform diverse array radars in civil systems carried by Unmanned Aerial Vehicles (UAVs),Autonomous Vehicles (AVs) as well as traffic control,where the antenna size is limited and the operating frequency band is precisely required.Moreover,it calls for the integration of radar and communication based on waveform diversity,because the waveform diverse array radars facilitate the radar spectrum management,especially in the growth of the competition for spectrum usage.

Many problems still remain unsolved,representing current challenges.Hence,the prospect of the range-dependent beampattern in waveform diverse array radars is far greater utilization of available DOFs in the range domain to enhance system performance and to even facilitate new operating modes.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgements

This work was supported in part by the National Nature Science Foundation of China (Nos.62101402,61931016,62071344),China Postdoctoral Science Foundation (Nos.2021TQ0261,2021M702547),and Young Elite Scientists Sponsorship Program by CAST (2021QNRC001).