Convex optimization of asteroid landing trajectories driven by solar radiation pressure

Chunjun DONG ,Hongwei YANG,* ,Shung LI ,Bo LI

a College of Astronautics,Nanjing University of Aeronautics and Astronautics,Nanjing 211106,China

b Tianjin Key Laboratory of Microgravity and Hypogravity Environment Simulation Technology,Tianjin 300458,China

c Tianjin Institute of Aerospace Mechanical and Electrical Equipment,Tianjin 300458,China

KEYWORDS Asteroids;Convex optimization;Optimal control;Soft landing;Solar radiation pressure;Trajectory optimization

Abstract High-area/mass ratio landers driven by Solar Radiation Pressure (SRP) have potential applications for future asteroid landing missions.This paper develops a new convex optimization-based method for planning trajectories driven by SRP.A Minimum Landing Error(MLE)control problem is formulated to enable planning SRP-controlled trajectories with different flight times.It is transformed into Second Order Cone Programming(SOCP)successfully by a series of different convexification technologies.A trust region constraint and a modified MLE objective function are used to guarantee the convergence performance of the optimization algorithm.Thereafter,the SRP-driven trajectory optimal control problem is converted equivalently into a sequence of convex optimal control problems that can be solved effectively.A set of numerical simulation results has verified the effectiveness and feasibility of the proposed optimization method.

1.Introduction

Due to the significant scientific value,especially in understanding the origin of life,exploration on asteroids has become a popular topic in recent years.1,2These asteroids exploration activities give human more opportunities to understand the vast solar system and the initial origin of life.Many space agencies all over the world have carried out some asteroid target exploring missions.For instance,NEAR-Shoemaker was the first asteroid-target exploring mission led by NASA.3Hayabusa achieved the first sample return mission,which was led by JAXA.4After the Hayabusa mission,Hayabusa-2 mission was started and came back to the Earth after finishing surface sampling in asteroid 162173 Ryugu.5,6Besides,OSIRIS-REx targeted at asteroid 101955 Bennu was launched by NASA in September 2016.7

Touching and landing on asteroids surface are conducive for sampling and obtaining more accurate scientific data than orbiting around asteroids.However,it is a great challenge for asteroid landing mainly due to the following reasons: the remote distances of asteroids,different sizes,irregular shapes,and highly irregular gravity fields.8Therefore,research on descent landing trajectory optimization for successfully landing on irregularly-shaped asteroids has attracted much interest and attention.Typically,both indirect and direct methods can be adopted for solving a trajectory optimization problem.9,10-Indirect methods can guarantee accuracy and optimality of a solution in theory.However,they often need a suitable initial guess for trajectory optimization,which makes it difficult to achieve fast convergence.11Direct methods often discretize the control and state of an original optimization problem with some ways and transform it into formulation of a nonlinear programming problem.However,the required computation time can be long because a large number of parameters are required for the discretization process.12

Due to the problem of communication delay,it is quite important for on-board guidance and trajectory optimization in asteroid landing missions.Recently,convex optimization has been widely applied in the aerospace field due to its mature theories and high computational efficiency.13,14Acikmese and Ploen firstly proposed the convex optimization of Mars powered descent trajectories through a Second Order Cone Programming (SOCP) problem.15Some other research has also been done to improve the method proposed by in Refs.16,17However,the gravity environment is considered to be constant in these studies,which is inapplicable for landing on irregular asteroids.One of the main differences between asteroids and planets is the irregularity of gravity.The gravity field near an asteroid is often highly nonlinear and irregular.For the convexification of the trajectory optimization problem with an asteroid’s highly irregular gravity field,a Successive Solution Method (SSM)18was adopted by Pinson and Lu.19Nonlinear dynamic equations thus were solved with the SSM,and they transformed the fuel optimal control problem for asteroid landing into a convex optimization problem successfully.Yang et al.presented a novel method for rapid generation of timeoptimal asteroid soft-landing trajectories based on convex optimization.20Chen et al.proposed an improved reachability analysis and convex programming method for minimum-fuel low-thrust trajectory optimization.21Zhou et al.presented a novel sequential convex programming method based on customized adaptive mesh refinement to achieve a good balance between solution accuracy and computational efficiency.22Zhang et al.presented a convex programming algorithm based on modified Rodrigues parameters for a six-degree of freedom asteroid powered landing trajectory design problem.23Song et al.proposed a powered descent guidance algorithm based on pseudospectral convex optimization to increase the accuracy and adaptability of the algorithm.24These studies of landing trajectory optimization on asteroids via convex optimization form the foundation of our current investigation.

Solar Radiation Pressure (SRP) is usually regarded as the primary perturbation for considering the dynamics in the weak gravity environments of irregular asteroids.Orbital dynamics near asteroids considering the strong effects of SRP were investigated in previous research,including several kinds of special orbits.25–29.Besides,some other researchers also investigated the attitude-orbit coupled dynamics for motions near asteroids,such as hovering over elongated asteroids,30hovering and orbiting operation,31and relative pose estimation.32

However,SRP on the other hand can be an effective source of active control force rather than a perturbation.The main advantage of SRP acceleration compared to other perturbations is that it can be controlled by a change of the spacecraft attitude.Recently,a future potential idea of area-of-effect softbots(AoES)for asteroid exploration led by the NASA Innovative Advanced Concept (NIAC) program was put forward.33In their proposal,SRP can be used to propel a lander with a high area/mass ratio during descent and surface hopping transfers.This new type of lander has a flexible design and has potential applications in future asteroid exploration.SRP can provide a considerable control authority in asteroids’weak gravity environments and save fuel consumption for a subsequent exploration mission.Specifically,AoES depends on SRP for control to land on the surface of an asteroid after being released at a proper altitude from the mothership to the surface of the target asteroid.Inspired by the new mission scenario of this future potential asteroid exploration concept,Oguri and McMahon developed a Lyapunov-function-based optimal control law for landing successfully on asteroid surface using SRP for control only.34However,the final landing position and velocity were uncertain,and the gravity was assumed to be a stochastic perturbation in their studies.

This paper aims to develop a rapid trajectory planning method based on convex optimization for landing at a particular site with zero relative velocity.To the best knowledge of the authors,little work has ever been published on the topic of addressing convex programming for SRP-driven asteroid landing trajectory optimization.Compared with previous studies on thrust-controlled asteroid landing,19,20the SRP-driven asteroid landing case raises new challenges and requires a new convex optimization-based method mainly due to the particularity of SRP control.SRP control acceleration has less degrees of freedom by its nature,which is controlled by only two angles.Moreover,the SRP acceleration magnitude is not a control variable but decided by the solar-asteroid distance and lander properties.These make it different from the traditional thrust-driven landing approach.Thus,previous convex optimization methods19,20were unable to solve this new SRP-driven trajectory optimization problem.,Song and Gong35proposed a convex optimization method for planning optimal interplanetary solar-sail trajectories.However,the flight time was limited to the minimum flight time in their work.In this paper,a convex optimization-based method for planning SRP-driven asteroid landing trajectories with a flexible flight time will be proposed.In addition,the influences of the parameters of Time of Flight (TOF) and SRP will also be investigated.

The rest of the paper is organized as follows.Section 2 briefly introduces dynamical models and equations adopted for this paper.In Section 3,an original non-convex problem and constraints are formulated.Section 4 introduces a series of different convexification technologies of converting the original non-convex optimization problem into a convex optimization framework.Different simulation situations are conducted and analyzed in Section 5.Section 6 concludes this paper.

2.Dynamical model

2.1.Equations of motion

An Asteroid-Centered Hill (ACH) frame34and an Asteroid-Centered Body-Fixed (ACF) frame are used,as shown in Fig.1.As for the ACH frame,the origin is located at the asteroid’s centroid,the axis xACHis the direction of the sun-asteroid vector,the axis zACHis the angular momentum of the asteroid about the Sun,and the axis yACHcompletes a right-handed system.As for the ACF frame,the origin is fixed at the asteroid’s centroid,the axis zACFis the asteroid’s spin axis,the axis xACFis the asteroid’s maximum inertial principal axis,and the axis yACFforms a right-handed system.The equation of motion for a lander in the ACF frame is as follows:30

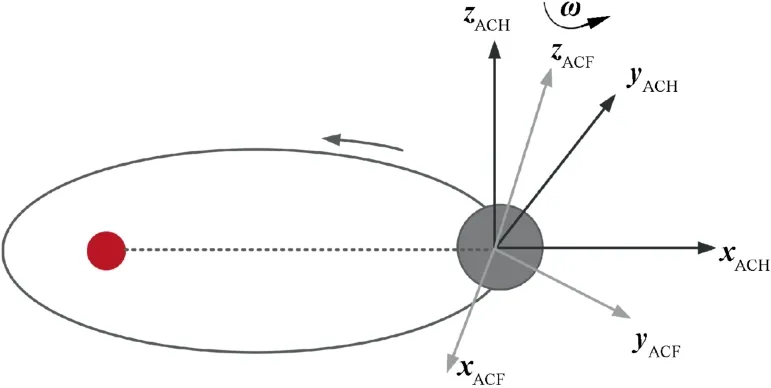
Fig.1 Schematic diagrams of the ACH and ACF frames.

The asteroid is considered to have a constant angular velocity ω about the axis zACF.Then Eq.(1) can be simplified to:

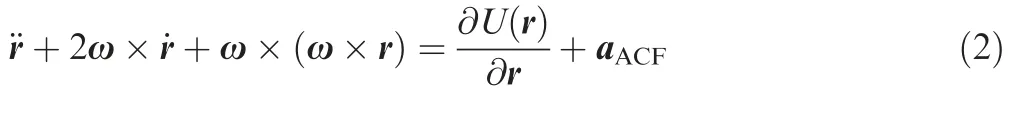
2.2.Gravity field model

The polyhedral-shape method is considered as a high-precision gravitational field model when near an irregular asteroid.36,37This method proposed by Werner and Scheeres is adopted to describe the irregular gravity near the target asteroid in this paper.The gravitational acceleration ∇Uthen can be expressed as:37

where ρ is the bulk density of the asteroid,Grepresents the gravitational constant,∇is the gradient operator,and Peand Qfare defined as:

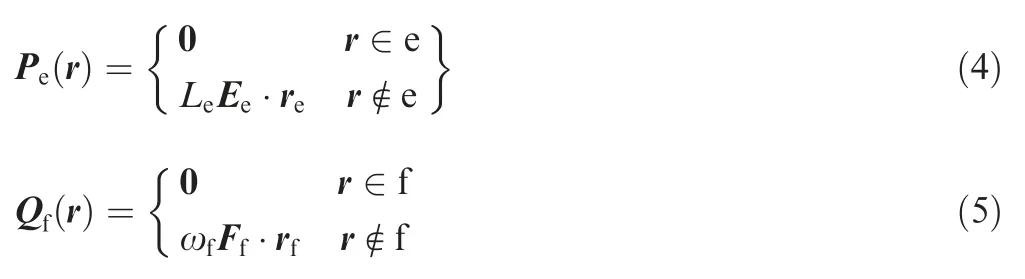
where subscripts e and f represent the edge and face of the polyhedral model,reand rfrepresent the vectors from the test point to the edge and the face,respectively.Eeand Ffare the tensors of the edge and the face,respectively.Leis an edge factor,and ωfis the solid angle.The value of ωfcan determine whether the position of the lander is inside the asteroid or not.

2.3.SRP model

For the motion in the vicinity of an irregular asteroid,the lander is assumed to be flat.The attitude of the lander is defined in the ACH frame with two angles: the pitch angle α and the clock angle β,as seen in Fig.2.α denotes the angle between the normal direction of the lander n and the axis xACH.β is the angle between the axis zACHand the projection of the normal direction n on the plane perpendicular to the axis xACH.In the ACH frame,SRP acceleration acting on the lander can be expressed as:33

Fig.2 Attitude definition of the lander.

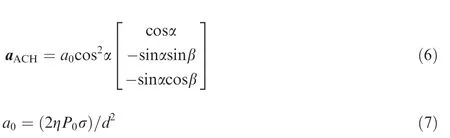
where 0 ≤α ≤π/2,0 ≤β ≤2π,η is the reflection coefficient of the lander,dis the asteroid-sun distance,P0is the solar constant,and σ represents the area/mass ratio of the lander.

3.Formulation of an original non-convex trajectory optimization problem

We consider the trajectory optimization problem of soft landing on the surface of a target asteroid.A soft landing means that a lander can achieve zero velocity relative to the asteroid surface when it finally reaches the landing site.Unlike a traditional lander,an SRP-driven lander has no fuel consumption,and fuel-optimal is invalid for this problem.A Minimum Landing Error (MLE) control optimization problem is adopted for planning the soft-landing descent trajectory in this paper,because the flight time for landing on an asteroid usually depends on many mission-relevant factors and a time optimal trajectory sometimes has its inapplicability.The flight time becomes fixed,and the optimal trajectories for different flight times are obtained by solving the MLE optimal control problem.The problem’s optimization objective is to minimize the position error and can realize soft landing at the final time.

The trajectory optimization problem is described in Eq.(8)through Eq.(14),which is denoted as Problem P1.

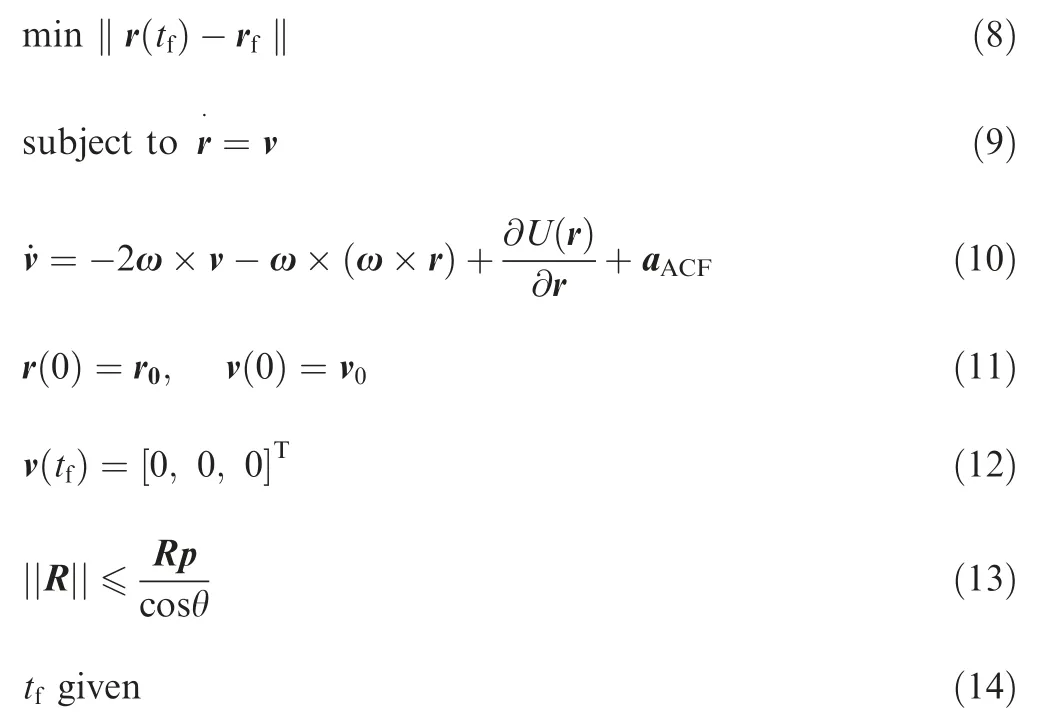
where r and v are the state vectors of the lander,and aACFis the control vector.r0and v0represent the initial position and velocity vectors of the lander,respectively,which are assumed to be known.The final surface landing site rfshould be preselected by considering some mission-relevant factors,such as local surface terrain conditions,communications,and scientific exploration value.v（tf）=[0,0,0]Tdenotes the final landing velocity constraint on the asteroid surface.tfrepresents the descent time which is specified in advance.

Besides,the constraint of Eq.(13)represents the constraint of a glide-slope,19which is illustrated in Fig.3.Its purpose is to prevent the lander from crossing below the surface and colliding with the asteroid before arriving at the target landing site.The cone angle θ is limited in the interval[0°,90°].The vector p is the unit normal vector of the target landing site,and the position vector R=r-rf.The angle between the vectors R and p is denoted as λ.The constraint λ ≤θ should be satisfied in the entire landing process.

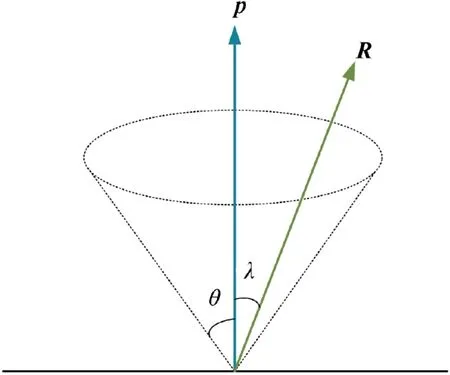
Fig.3 Glide-slope constraint.

The above mentioned MLE control problem P1 is nonconvex due to the following factors.Firstly,the irregularity of the gravitational field near the target asteroid makes the dynamic equations to be nonlinear.Secondly,the SRP acceleration has less degrees of freedom,which is controlled by only two angles.In addition,the pitch angle α determines the magnitude and direction of the SRP acceleration in Eq.(6) at the same time.These factors make the SRP acceleration to be another main nonlinear term that leads the original problem to be a non-convex optimization problem.Thus,some considerable efforts and techniques are required to convert the original trajectory optimization problem P1 into a problem that can be solved by convex optimization.

4.Convexification of the non-convex optimization problem

In order to solve the trajectory optimization problem by convex optimization,a series of techniques is used to handle nonlinearities in the original non-convex problem P1.In this section,an SSM is adopted to address the nonlinearity caused by the irregular gravitational filed.19Next,a method of changing variables is adopted for the nonlinear SRP acceleration,and then successive linearization is used to handle the nonlinear control constraints.Additionally,the trust region constraint and a modified MLE objective function are applied for improving the convergence performance and the effectiveness of the proposed trajectory optimization algorithm.

4.1.Successive solution method

In this part,the SSM is used to address the non-convexity problem caused by the nonlinear irregular gravitational acceleration.19According to the results obtained from the previous iteration,dynamic Eqs.(9) and (10) in Problem P1 are rewritten as:

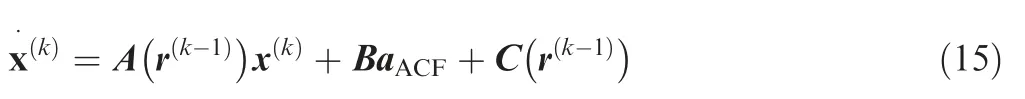
wherekandk–1 represent current and previous iterations,respectively,x=[r,v] represents the state vector,and the matrices of A,B,and C are shown as follows:20

The linear interpolation from r0to rfis used for the initial reference trajectory in this paper.When a specified tolerance is satisfied between previous and current iterations,the iterations process will stop.The problem of nonlinear irregular gravitational acceleration is then solved by the SSM successfully.19

4.2.Successive linearization

For the SRP-driven lander,SRP is the only applied force for maneuver during the landing process.In this part,convexification of the nonlinear SRP acceleration is made.

The first step of the convex process is to denote the SRP acceleration with other mathematical forms,and the method of changing variables is adopted.35

We introduce a new control variable u andas follows:

Then the SRP acceleration can be rewritten as:

A nonlinear essential equality constraint Φ on the variable u is shown as:

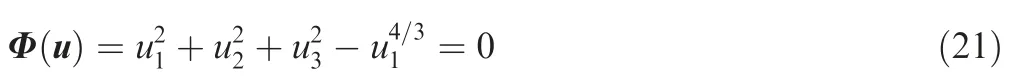
This nonlinear control constraint equation needs to be handled to achieve the formulation of convex optimization.A successive linearization method is introduced to handle this nonlinear control constraint problem.18

The nonlinearity of control constraints for Eq.(21) will be satisfied successively with the following successive linearization process:

where δu is the variation of u in two adjacent iterations,and Dk-1is the Jacobian matrix of Eq.(21),which is obtained from the solution u of the last iteration as follows:

4.3.Discretization

The dynamics are now linear with the above methods we adopted.A discretization process is executed for satisfying the solver requirements.The given descent time is uniformly divided into N intervals with a fixed dttime step,and then the trajectory between neighboring points will be propagated by adopting the following trapezoidal rule:19

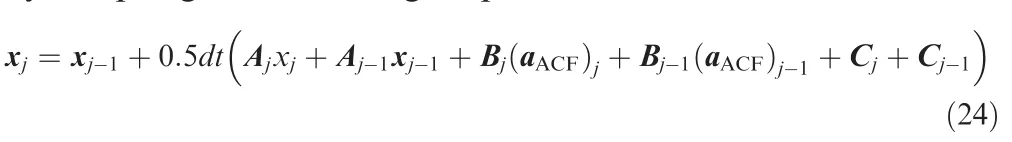
wherejandj–1 denotes current and previous points,respectively.x0represents the initial state of the lander.Based on Eq.(24),the current point will be obtained according to the previous point and matrices A,B,and C as follows:

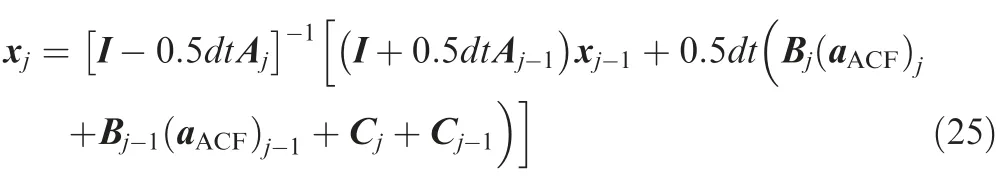
where I represents an identity matrix.

4.4.Trust region constraint

The trust region constraint is adopted in this paper to avoid the potential risk of an unbounded linearization process and improve the convergence performance.38Then,an additional constraint is added,which is as follows:

where ηuis the trust region radius that restricts the control input.In this way,new states would not excessively deviate from previous ones.

Besides,due to the additional trust region constraint,the original objective function in Eq.(8) should be adjusted to improve the convergence performance and the effectiveness of the proposed trajectory optimization algorithm.A modified MLE objective function is applied,which is given by:

where ηuis the trust region radius mentioned previously,andwuis the penalty parameter.

After the above convexification processes,a modified MLE control problem P2 shown in Eq.(28) through Eq.(38) is obtained.Eqs.(34) and (36) denote the upper and lowerbounds of the control,respectively.Problem P2 is in an SOCP format and can be solved by convex optimization.

5.Simulation results

In this section,we will present numerical simulation results and show the effectiveness and feasibility of the proposed optimization algorithm for SRP-driven landing trajectory optimization.The MATLAB CVX package is adopted for solving this problem.39Asteroids 2063 Bacchus and 101955 Bennu are selected as the target landing bodies.More information about the shape data of these two asteroids could be found in Refs.40 and 41.In the simulations,a tolerance of the landing error is given.The landing velocity tolerance is set to 10-5km/s.Iterations will stop when the position error between previous and current iterations is less than ε=10-5km apart at every point.The values of other parameters for the simulation are shown in Table 1,where AU is the Astronomical Unit.The solving process will repeat until the algorithm convergence criteria are met.The solving process is as follows:

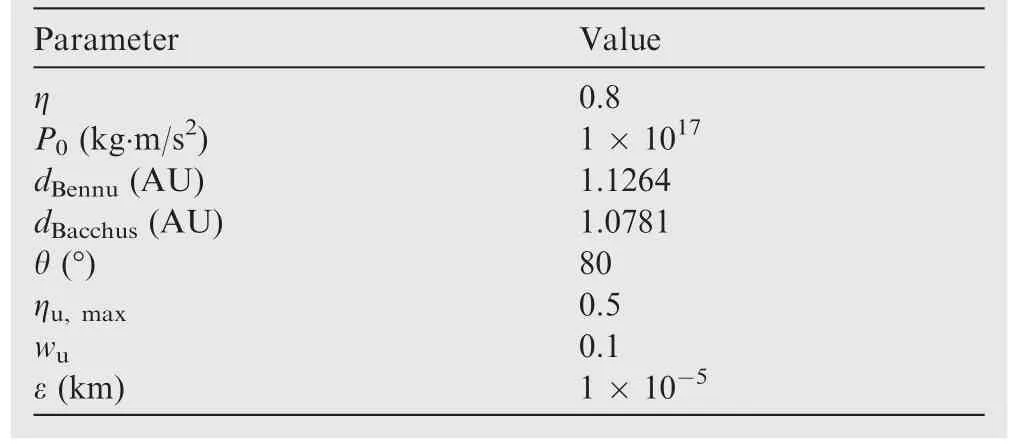
Table 1 Numerical simulation parameters.

Table 2 Simulation parameters for Scenario 1.

Table 3 Simulation parameters for Scenario 2.

Step 1.Given an initial reference solution rrefand urefbefore the first iteration.

Step 2.Initialize the trust region radius ηu.

Step 3.Start the first iteration process and obtain a solution r1and u1;update the trust region radius ηu.

Step 4.In thekth iteration process,update the reference solution with the (k-1)th iteration result.

Step 5.

5.1.Application for asteroid 101955 Bennu (Scenario 1)

In this simulation scenario,the lander is considered to descend from a body-fixed hovering status.The final target landing site is preselected,and the simulation parameters for Scenario 1 are shown in Table 2.

Table 4 Simulation parameters for Scenario 3.

The results of the position,velocity,control,and landing trajectory of the MLE control optimization problem are shown in Fig.4.These results show that the lander can achieve soft landing on the target landing surface finally.According to the control result of the MLE control problem we obtained,the integral process for the initial dynamic equations,Eqs.(9) and (11),is conducted for revealing the accuracy of the SRP acceleration result and obtaining the recursive dynamic trajectory.The two obtained trajectories are shown in Fig.5.As can be seen,the recursive dynamic trajectory is very consistent with the MLE trajectory.The terminal position deviation between these two trajectories is less than 0.05 m after calculation.

Fig.4 Results of the MLE control problem for Scenario 1.

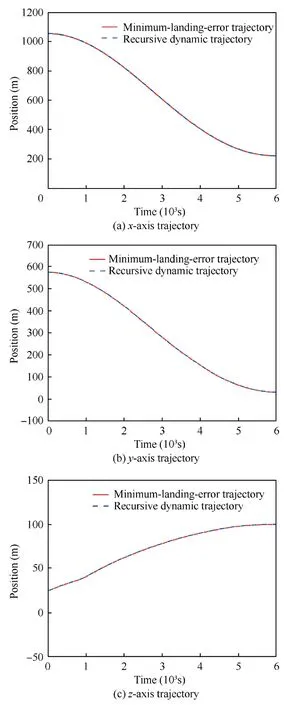
Fig.5 Recursive dynamic trajectory histories for Scenario 1.

The magnitude of the trust region in the iterative process is presented in Fig.6.The proposed optimization algorithm converges after 14 times iteration,and the trust region will finally approach zero after required iterations for the heavy penalty used in the enhanced objective function.Thus,the constraint of the trust region can increase the problem’s convergence performance in the iterative process.

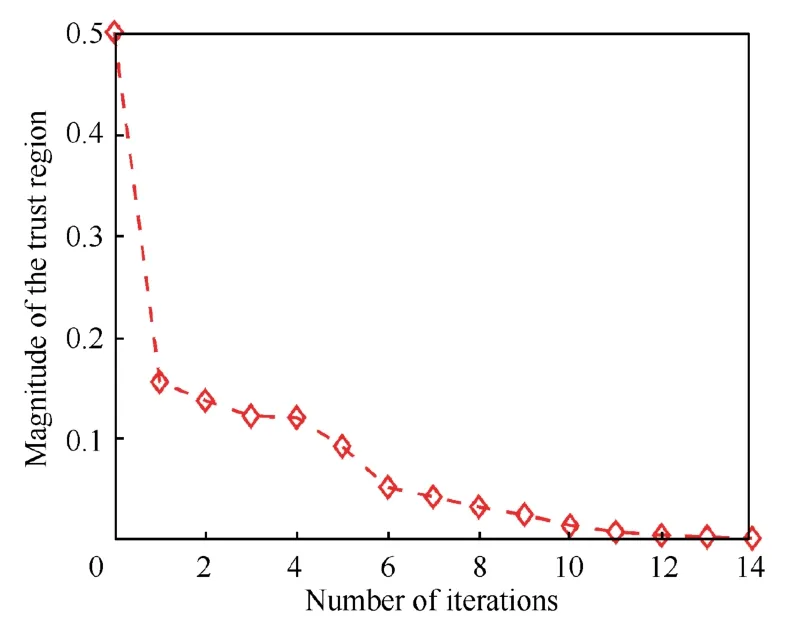
Fig.6 Magnitude of the trust region in the iterative process for Scenario 1.

The numerical simulation results above validate the effectiveness and feasibility of the proposed optimization algorithm for the current scenario.In the following simulations,we will discuss the convergence performance and effectiveness with different simulation parameters and scenarios.

5.2.Application for asteroid 101955 Bennu with a non-zero initial velocity (Scenario 2)

In this simulation scenario,the lander is assumed to descend from a non-hovering status to show the feasibility of the proposed optimization algorithm.The simulation parameters for Scenario 2 are set as in Table 3.

The final solutions of the MLE control problem are presented in Fig.7.It shows that the lander can land at the target position at the final time while it can achieve zero velocity relative to the target landing site for the current simulation scenario.The trajectory of the MLE control problem is basically consistent with the solution of the recursive dynamic trajectory,as shown in Fig.8.After calculation,the terminal position deviation between these two trajectories is less than 0.1 m.Overall,12 iterations via convex optimizations are required to achieve convergence in Fig.9.

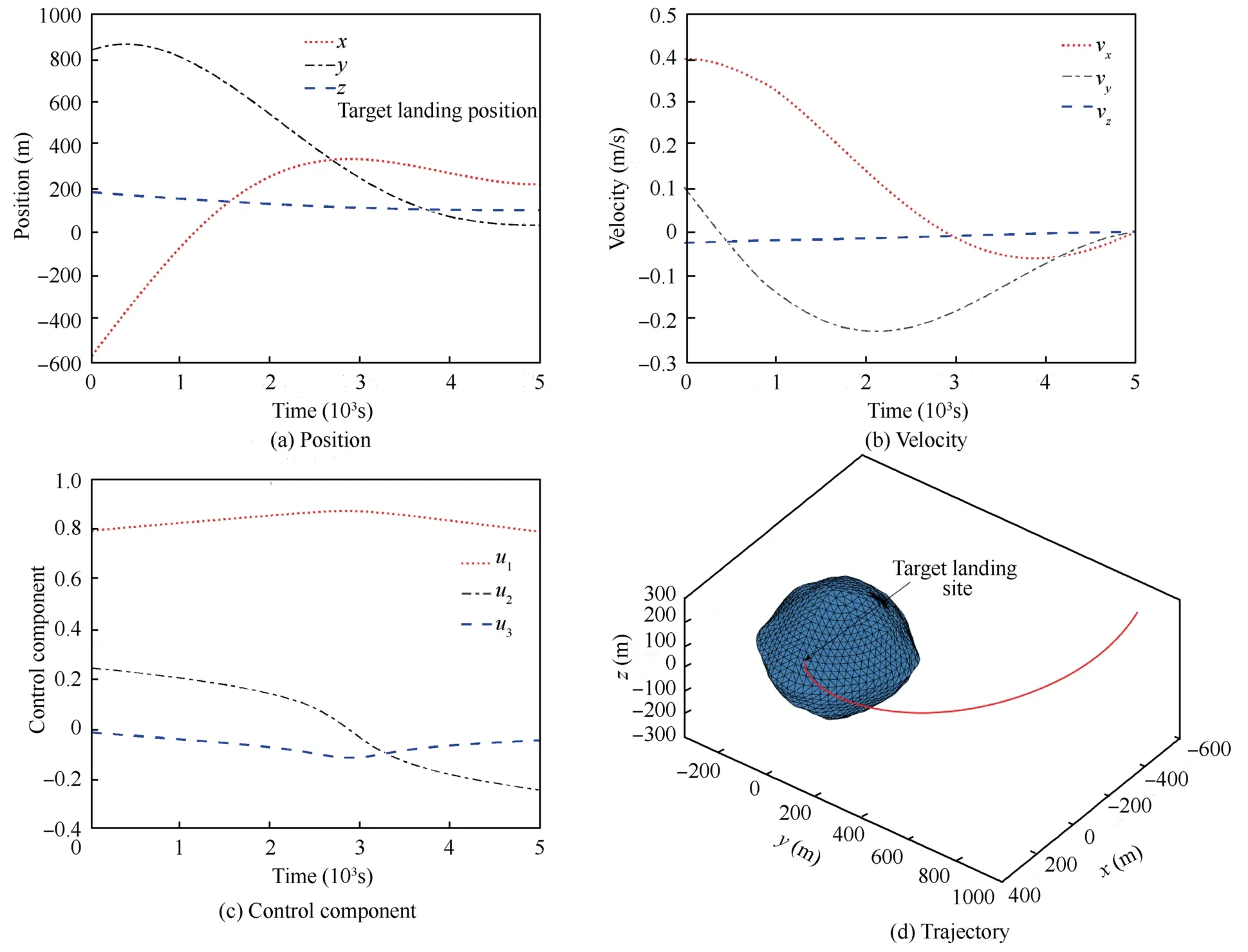
Fig.7 Results of the MLE control problem for Scenario 2.

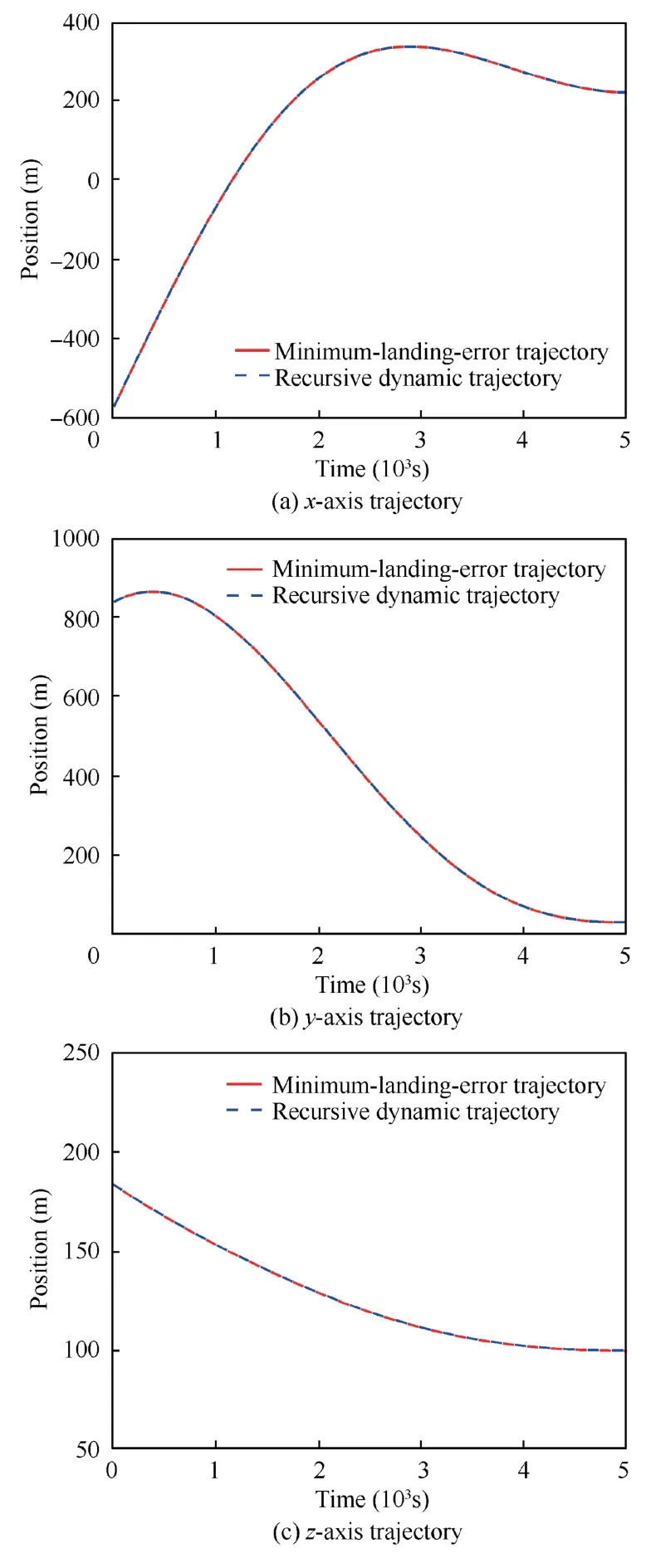
Fig.8 Recursive dynamic trajectory histories for Scenario 2.

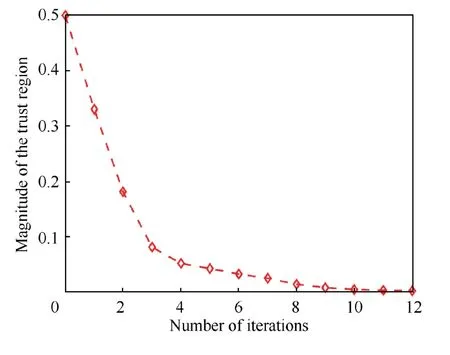
Fig.9 Magnitude of the trust region in the iterative process for Scenario 2.

5.3.Application for asteroid 2063 Bacchus with a high area/mass ratio (Scenario 3)

The area/mass ratio is important in determining the maximum available magnitude of the SRP acceleration,as can be seen from Eqs.(6) and (7).A relatively high area/mass ratio of a lander design can provide a considerable capability-orbit transfer and surface hopping trajectory control for asteroid exploration using SRP forces.33A preliminary study of the NIAC AoES concept has shown that the value of a high area/-mass ratio would be feasible to achieve in reality.33In order to show that the proposed algorithm is still effective,the simulation parameters adopted for scenario 3 are shown in Table 4.

The results in Fig.10 indicate that the lander can still achieve soft landing on the asteroid surface for this simulation scenario.The same integral operation is also performed.

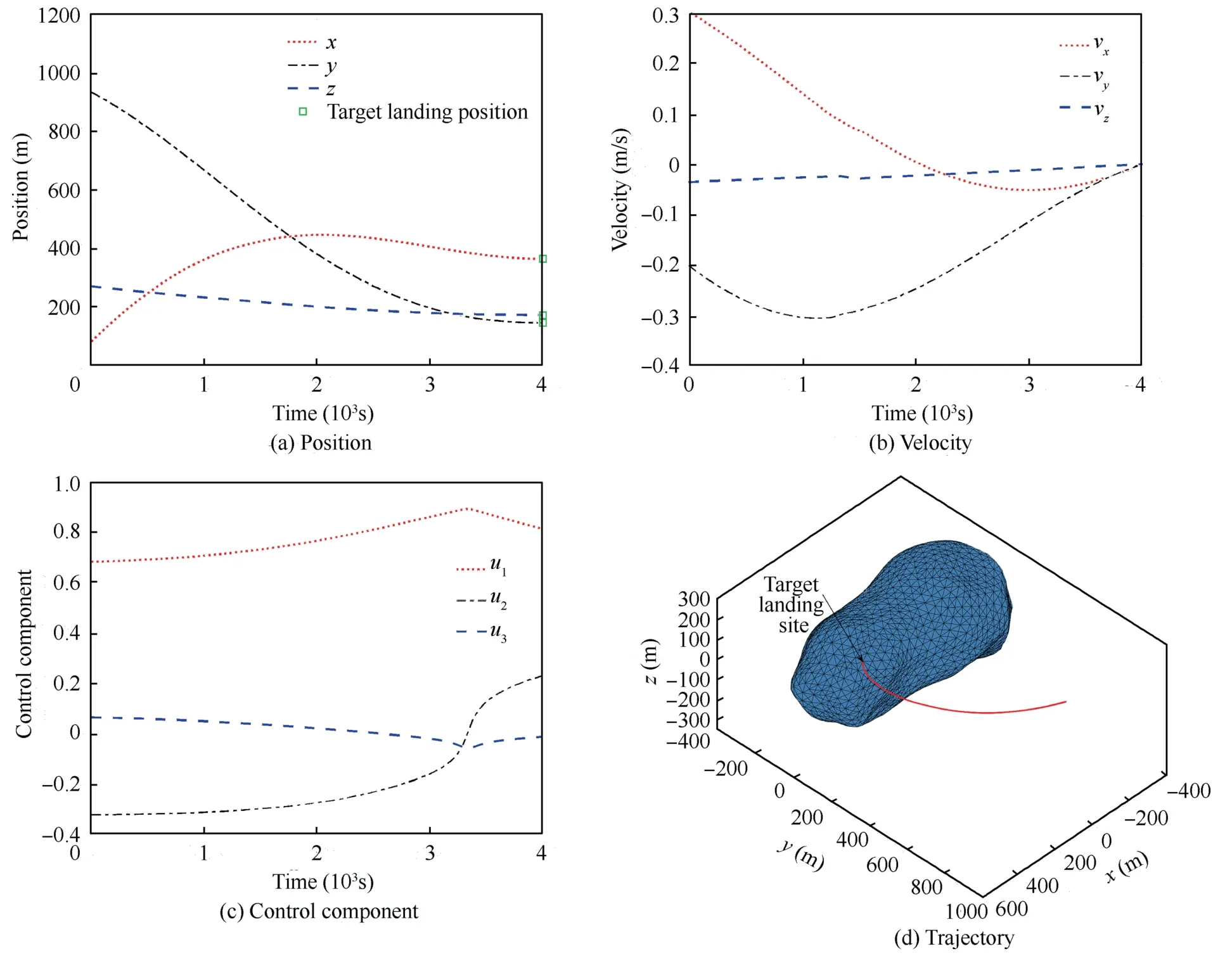
Fig.10 Results of the MLE control problem for Scenario 3.

As shown in Fig.11,the MLE and recursive dynamic trajectories are also basically consistent with each other.The terminal position deviation of these two trajectories is less than 0.05 m after calculation.Moreover,according to the change of the magnitude of the trust region in the iterative process illustrated in Fig.12,convex programming with the proposed optimization algorithm indicates a satisfying convergence performance,and 11 times iterations are needed for the optimization process.

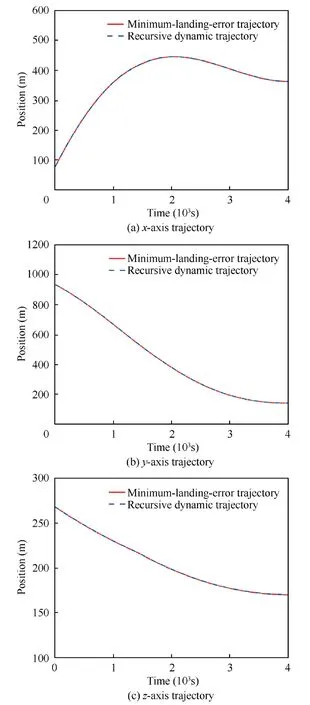
Fig.11 Recursive dynamic trajectory histories for Scenario 3.

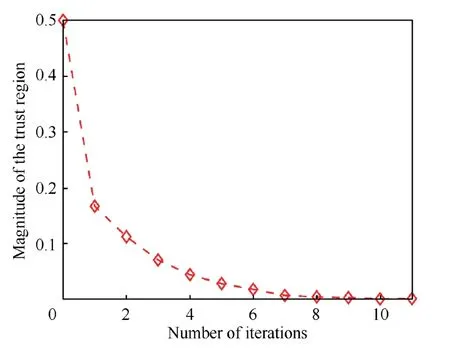
Fig.12 Magnitude of the trust region in the iterative process for Scenario 3.

5.4.Parameter analysis

The available soft landing trajectories for different parameters are discussed in this part.The descent duration and the area/-mass ratio are varied in an admissible range.The descent duration is chosen betweentf∈[1000,10000] s,and the area/mass ratio varies between σ ∈[0.1,2]m2/kg.To investigate the influences of the descent duration and the area/mass ratio,the initial position is fixed,and the lander descends in a body-fixed hovering status.A sensitivity analysis is conducted by running the algorithm on a grid of the descent duration and the area/-mass ratio.Fig.13 shows the results for different initial conditions.

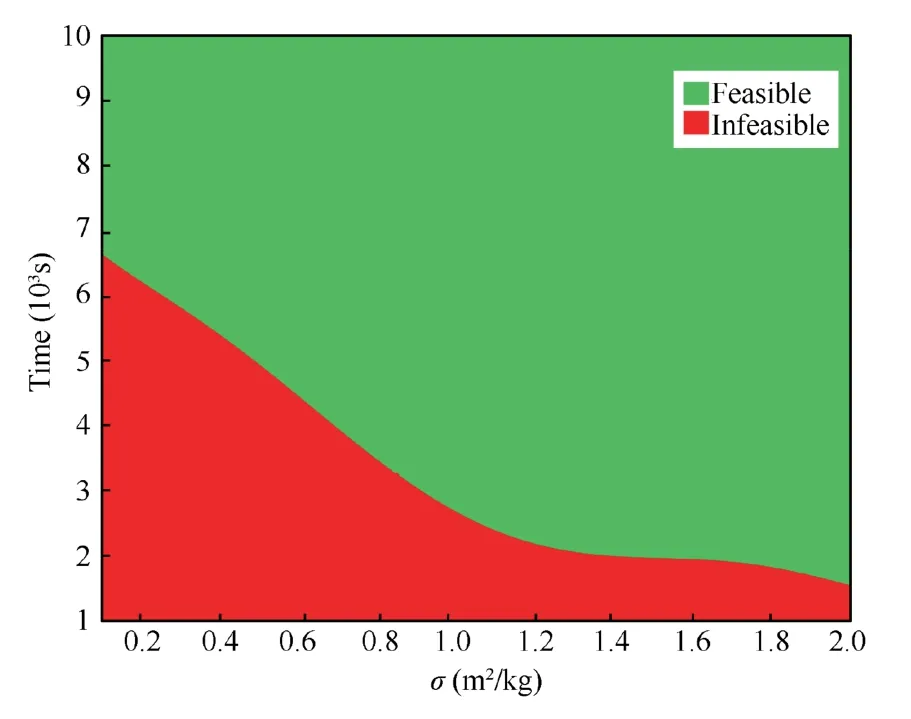
Fig.13 Results for different initial conditions.

It is found that the whole design space can be divided into two regions.The green region represents that the lander can achieve soft landing on asteroid surface;on the contrary,the red region can’t.It is difficult to find a feasible solution if the selected descent duration is less than the specific value for different area/mass ratios.One possible exploration may be that the used SRP cannot complete asteroid surface soft landing in a short descent duration.Therefore,the descent duration should be set appropriately longer to obtain a feasible soft landing trajectory.Besides,it is found that the required minimum descent duration decreases as the area/mass ratio increases,so a higher area/mass ratio can provide a more considerable SRP acceleration and make the descent duration have more flexible options.

Based on the results in Fig.13,to investigate the influence of the descent duration specifically,the area/mass ratio of the lander is set as σ=0.8 m2/kg.The lower bound value of the descent duration range is set to be 5000 s to ensure it converge to a feasible solution according to numerical simulations.The upper bound value of the range is set to be 10000 s.Fig.14 shows the deployment soft landing trajectories to the surface of asteroid 101955 Bennu with different descent durations.The results shown above validate that the lander can achieve the goal of soft landing accurately on the target asteroid surface with different landing trajectories for different selected descent durations.It indicates the feasibility of the proposed algorithm to different initial conditions.

Fig.14 MLE descent trajectories with different descent durations (σ=0.8 m2/kg).

Thus far,simulation scenarios presented above have shown that the proposed optimization algorithm can achieve SRPdriven trajectory optimization for soft landing on asteroid surface effectively.These scenarios have shown the effectiveness and feasibility of the proposed optimization algorithm for convex programming,and optimal solutions can be obtained by at most 14 times of convex optimization.These results also show that it is a promising approach in applying SRP under the weak gravity environments of asteroids for future asteroids exploration missions.

6.Conclusions

In this paper,a new SRP-driven trajectory optimization algorithm for asteroid surface soft landing based on convex optimization is proposed.The SRP is utilized as a source of active control force in the proximity of asteroids instead of a primary perturbation for a lander.An MLE control problem is formulated for asteroid soft landing trajectory planning.The polyhedral model is adopted as an accurate gravity field model in the optimization process.For the original nonconvex problem,a series of different convexification technologies is adopted to transform the original non-convex optimization problem into the formulation of SOCP that can be handled with convex optimization effectively.

Moreover,a trust region constraint and a modified MLE objective function are used for improving the convergence performance of the proposed optimization algorithm.Results show that the lander can reach the landing site softly at the final time.Simulation scenarios indicate that this method yields low errors.Trajectories coincide quite well between the solutions of the MLE control problem and recursive dynamic.The maximum terminal position deviation of these two methods is less than 0.1 m in the simulations.The proposed algorithm can converge after at most 14 times iterations in the simulations.A parameter analysis indicates the feasibility of the proposed optimization algorithm to different initial conditions.Numerical simulation results validate the effectiveness and accuracy of the proposed optimization algorithm,which also show the potential application and possibility in using an SRP-driven lander in a weak gravity environment for future exploration of asteroids.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgements

The work was supported by the National Natural Science Foundation of China (No.12102177),the Natural Science Foundation of Jiangsu Province,China (No.BK20180410),the Young Elite Scientists Sponsorship Program by CAST,China (No.2018QNRC001),the Open Project Program of Tianjin Key Laboratory of Microgravity and Hypogravity Environment Simulation Technology,China (No.WDZL-2020-07),and the Foundation of Graduate Innovation Center at NUAA,China (No.kfjj20201503).