考虑摆线轮磨损的RV减速器传动精度可靠性分析与参数优化

刘 江，肖正明，张龙隆，刘卫标

（1.昆明理工大学机电工程学院，云南昆明 650500；2.云南昆钢重型装备制造集团有限公司，云南昆明 650501）

精密减速器是工业机器人的重要组成部件，控制着机器人的重要性能。行星摆线减速器也称为RV（rotate vector）减速器，被广泛应用于机器人关节，它的传动精度影响着机器人的运动精度。工业机器人因其工作需求会频繁地进行往复运动，对RV减速器的回差精度要求极高。因此，有必要明晰影响RV减速器回差精度的静、动态因素，从而采取针对性的措施去提高减速器的传动精度，并延长其使用寿命。

机器人的运动性能由高精密减速器的侧隙和扭转刚度控制[1]。零件的制造、装配误差，摆线轮的修形及其在啮合过程中的变形、磨损等都会产生间隙。Yang、Blanche等[2-3]对具有加工公差的摆线针轮减速器进行了运动学分析，获得了零件公差、传动比与间隙之间的关系。任重义等[4]分析了摆线轮齿廓的修形方法以及制造、安装误差对几何回差的影响，研究表明摆线轮不同相位的几何回差是有差异的。Lin等[5]利用蒙特卡罗方法分析了零件几何参数和公差分布对摆线针轮减速器运动误差分布的影响，并在此基础上建立优化模型对零件几何参数进行了优化。曹代佳[6]以许用回差精度为约束，对RV减速器关键零部件进行公差分配和优化，并通过实验验证了优化结果的合理性。Chu等[7]提出了一种基于遗传算法的选择性装配方法，有效提高了RV减速器的回差精度。陆龙生等[8]把摆线轮与针齿接触产生的形变量等效叠加到摆线轮的齿廓上，结合“等距+移距”组合修形，在保持摆线针轮径向间隙不变的情况下实现了回差的优化。

针对机械磨损，许多学者根据不同的磨损机理建立了数学模型，其中Archard磨损模型被广泛应用。Archard[9]基于黏着磨损理论推导出定量计算磨损体积的数学模型。基于Archard磨损公式和Hertz接触理论，张俊等[10]计算了在准静态工况下直齿圆柱齿轮的磨损量，苏建新等[11]建立了摆线轮磨损量的计算模型。Shen等[12]将有限元理论与数值模拟方法相结合，提出了一种预测机械零部件磨损的新方法。李聪波等[13]对Archard模型进行修正，并在ANSYS软件中模拟机床导轨的磨损，预测了导轨的早期磨损量。

RV减速器的传动误差包括由各零件制造、装配误差引起的静态误差和由时变啮合刚度、零件弹性变形以及摩擦磨损引起的动态误差。现有研究主要从提高RV减速器传动精度的角度展开，静、动态误差都有涉及，但鲜有学者从关键零件的磨损出发研究动态误差对回差精度的影响。本文综合考虑摆线针轮传动机构的加工误差、配合间隙和摆线轮的磨损，开展RV减速器传动精度可靠性研究，以期为摆线轮轮齿的减磨延寿及高精度RV减速器的设计提供新思路。

1 摆线轮磨损量的数值计算与预测

1.1 摆线轮接触压力的计算

摆线针轮传动属于多齿啮合传动，其啮合情况复杂，一般采用数值方法求解啮合力。首先计算最大啮合力Fmax的初值Fmax0，并由Hertz接触公式求得受力最大处啮合点的形变量δmax。

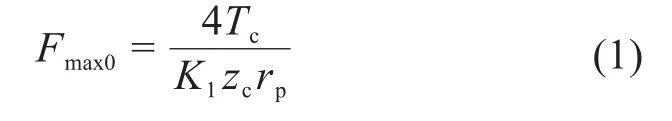
式中：Tc为摆线轮传递的转矩；K1为短幅系数；zc为摆线轮齿数；rp为针齿中心圆半径。

考虑到摆线轮修形会产生侧隙，假设理论啮合点所受啮合力Fi和形变量与初始侧隙的差值成正比，其线性关系式为：

式中：i为啮合相位角为ψi的啮合点；δi为理论啮合点的形变量或法向总位移；Δsi为理论啮合点的初始侧隙。

形变量大于侧隙的理论啮合点在传动过程中都会啮合，以此可以判断摆线针轮的啮合区域和同时啮合的齿数。依据摆线轮所受啮合力和啮合齿数列出力矩平衡方程：

式中：li为理论啮合点公法线到摆线轮中心的距离；M、N均为啮合区域内针齿的编号。

变换式(3)，可得：

式中：lmax为摆线轮节圆半径。

比较Fmax0与Fmax的数值。如果两者不相等，则将Fmax作为初始值重新输入，再次求解Fmax，直到Fmax0与Fmax相等时输出最终的Fmax，进而通过式(2)求得不同啮合位置的啮合力。

在啮合力作用下，摆线轮与针齿啮合处会形成一个接触面。摆线轮轮齿接触面上法向平均接触压力pi为：

式中：b为接触半宽；B为摆线轮齿宽。

1.2 滑动距离的计算

摆线轮与针轮在实际啮合中除了纯滚动，还存在相对滑动，在滑动的过程中伴随着摩擦磨损。摆线轮与针轮的相对滑动速度νr为：

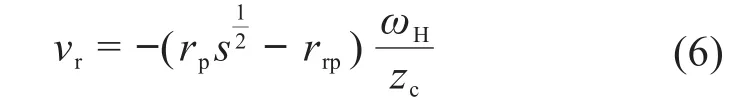
式中：rrp为针齿半径；s=1+K12-2K1cosψi；ωH为曲柄轴角速度。

滑动系数表示单点从进入到退出的啮合过程中相对滑动所占的比例。在接触宽度相同的情况下，滑动系数越大，摩擦距离越大。相对滑动速度νr与摆线轮切向速度νt的比值即为滑动系数λ，即：

单点啮合1次滑动的距离du为：

1.3 磨损系数的计算

磨损系数是受多重因素影响的动态变量，往往须针对具体对象通过实验设计来获取。Janakiraman等[14]通过多组磨损实验确定了在不同工况和接触条件下的磨损系数。利用Janakiraman总结的回归公式(9)可以对材料的磨损系数k进行估算。

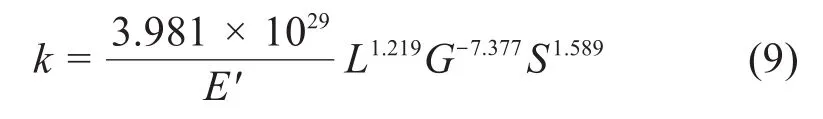
式中：L为无量纲载荷；G为无量纲压力-黏度系数；S为无量纲复合表面粗糙度；E′为等效弹性模量。

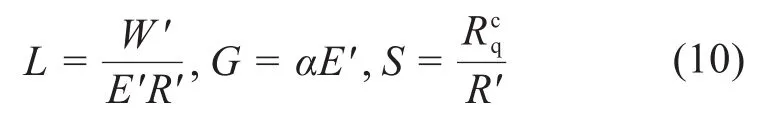
式中：W′为单位线载荷；R′为等效曲率半径；α为黏压系数；为复合表面粗糙度。

影响磨损系数的3个无量纲参数中，G的影响最大，L的影响最小，S的影响介于两者之间。同批次生产的减速器在相同工况下运行，如选用性能不一的润滑剂进行润滑，则零部件的磨损情况会呈现较大的差异。

1.4 磨损量的计算

Archard磨损模型可以表示为：

式中：V为磨损体积；u为滑动距离；K为磨损因子；W为载荷；H为材料硬度。

法向磨损深度h、磨损系数k、接触压力p可以表示为：

式中：A为接触面积。

利用式(11)、式(12)得到某个啮合点啮合1次所产生的磨损深度dh为：

由摆线针轮传动原理可知，曲柄轴带动摆线轮公转(zp-1)个针齿时摆线轮上所有齿均参与1次啮合，由此可得摆线轮的啮合周期t为[15]：

式中：zp为针齿数。

摆线轮轮齿磨损后齿廓初始侧隙会变大，接触压力也会发生变化，此时须重新计算接触压力pi和磨损深度h。当磨损累积量较小时，各点的接触压力变化较小，因此通常会设置一个磨损阈值ε，在达到该阈值之前可以近似认为单个啮合点啮合1次产生的磨损量不变。将磨损累积过程分成Q段，磨损间隔时间称为重构周期tq。tq时间内单个啮合点的累积磨损量hq为：

工作时间内单点总的磨损深度为：

式中：q为重构次数,q=1,2,…,Q。

等距、移距修形量会影响同时啮合的齿数和轮齿所受啮合力，从而进一步影响摆线轮的磨损，因此有必要探讨修形参数对齿廓磨损深度的影响。某RV减速器的参数如表1所示。首先通过搜寻条件（式（17））得到等距修形值的取值范围[-0.053，0.011]mm。由于初始径向间隙不变，移距修形量也就确定了。

表1 某RV减速器参数Table 1 Parameters of a RV reducer

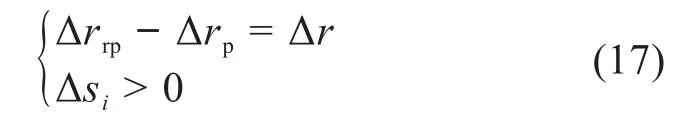
式中：Δrrp为等距修形量；Δrp为移距修形量；Δr为初始径向间隙。

将等距修形的取值区间等分，分析摆线轮在不同“等距+移距”组合修形下的受力，并计算摆线轮转动100 h时的磨损量。均匀选取其中6组数据，求出不同修形量下（以“等距修形量，移距修形量”表示）摆线轮的受力和磨损量，分别如图1和图2所示。由图1可知，在额定工况下，未磨损的摆线轮所受的啮合力沿齿廓方向先增大后减小。由图2可知，齿廓上磨损量的变化趋势与啮合力一致，最大磨损量出现在接触区域中间的位置。比较图1和图2中各曲线的峰值和分布规律可知，等距修形值越大，则最大啮合力越小，啮合区域越大，齿廓最大磨损量越小，齿廓上的磨损分布越均匀。

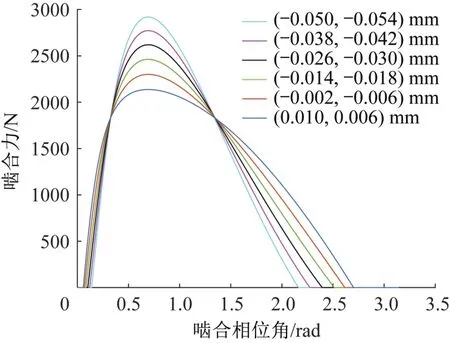
图1 不同修形量下摆线轮的受力Fig.1 Force on cycloidal gear with different modification amount

图2 不同修形量下摆线轮的磨损量Fig.2 Wear amount of cycloidal gear with different modification amount

1.5 磨损量预测

齿轮磨损是一个累积的过程，而磨损量又会影响轮齿的受力，因此计算累积磨损量时须多次重构齿廓以及重新求解啮合点的法向载荷，这在进行数值仿真计算时将耗费大量时间。高斯过程回归模型适用于计算量大且无法提供大量样本的情况[16]，能基于有限的仿真数据对输出响应进行预测。在创建数据样本时应适当缩短齿廓重构的周期，以提高磨损量计算及预测的精确性。

磨损随机过程服从正态分布[17]。建立磨损仿真值wo与磨损预测值wp的联合高斯分布：

式中：Koo为观测输入值的方差；Kop、Kpo分别为观测输入值和预测输入值的协方差；Kpp为预测输入值的方差；I为单位矩阵。噪声ζ～N(0,σ2)，其中0为均值，σ2为方差。

得到磨损预测模型为[18]：

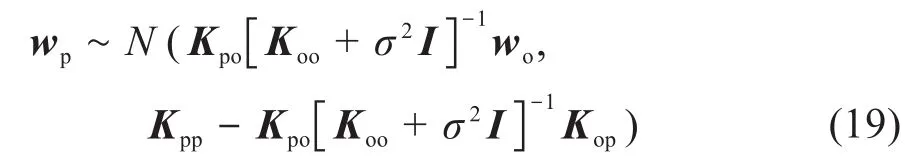
用观测样本训练磨损预测模型，然后根据训练好的预测模型和已知的预测输入值预测磨损量。模型的输入是减速器的负载Tz、转速n、工作时间T、摆线轮的等距和移距修形量，模型的输出是对应的磨损量预测值。

将Tz=3 136 N·m，n=15 r/min，T=3 000 h，Δrrp=-0.026 mm，Δrp=-0.030 mm时摆线轮磨损量的仿真值与预测值进行对比，如图3所示。图中灰色区域为预测值95%置信区间，可见各时间点的仿真值都在该区间内，预测结果的准确度较高，故该模型可以用于磨损量的预测。

图3 摆线轮磨损量仿真值与预测值的对比Fig.3 Comparison between simulation value and prediction value of cycloidal gear wear

2 考虑摆线轮磨损的传动精度动态可靠性分析

2.1 含磨损的传动精度模型的建立

RV减速器的误差因素及其引起的法向侧隙如表2所示[8]。通过Archard磨损模型计算而得的磨损深度是沿啮合点公法线方向的[19]，磨损引起的法向侧隙等效于等距修形引起的法向侧隙。

表2 RV减速器误差因素引起的法向侧隙及各误差的灵敏度指数Table 2 Normal backlash caused by RV reducer error factor and sensitivity index of each error

回差是表征RV减速器传动精度的重要指标。由侧隙引起的总回差Δφ为：

式中：Δβj为各误差因素引起的侧隙；iH为减速器传动比；r1为太阳轮分度圆半径；e为曲柄轴偏心距；a为太阳轮与行星轮的中心距。

2.2 传动精度动态可靠性分析

零件尺寸偏差、磨损量是服从某一分布的随机变量。在这些不确定因素影响下，减速器的回差会在一定范围内变动，一次简单的测量无法反映减速器传动精度的一般水平。因此，从概率统计的角度出发，建立传动精度动态可靠性模型，用不同时刻的精度可靠度来反映减速器传动精度动态变化情况。

考虑摆线轮磨损的传动精度动态可靠性的功能函数为：

式中：x=(Tz，n，T，Δrrp，Δrp)；Δφper为许用回差。

g(x,Δφper)＞0表示减速器传动失效。采用蒙特卡洛法对零件加工误差以及不同时刻的最大磨损量进行d次抽样[5]，将d个样点值代入总回差Δφ的计算式中，统计处于失效状态的样点数dT。则随时间变化的传动精度可靠度RT可以表示为：

RV减速器误差项的偏差值及其分布特征如表3所示[20]。设置工况为：Tz=3 136 N·m，n=15 r/min，用蒙特卡洛法抽样得到RV减速器回差模拟图，如图4所示。由图可知，摆线轮未磨损时，RV减速器的回差均值为0.7′左右，最大回差小于许用回差值1′，因此能够满足精度要求。

表3 RV减速器误差项的偏差值及其分布特征Table 3 Deviation value and distribution characteristics of error term of RV reducer 单位：mm

图4 RV减速器回差模拟图Fig.4 Backlash simulation diagram of RV reducer

RV减速器精度可靠度随工作时间的变化曲线如图5所示。由图可知：减速器工作4 000 h后，精度可靠度开始下降；当摆线轮累积磨损达6 000 h时，精度可靠度仅为88.7%，不能满足可靠性要求，因此须对减速器原参数进行优化。

图5 RV减速器精度可靠度随工作时间的变化曲线Fig.5 Variation curve of accuracy reliability of RV reducer with working time

2.3 参数的灵敏度分析

为了提高优化效率，须对参数进行灵敏度分析，以优先考虑对回差影响较大的设计参数。以总回差对各误差项求偏导，则各误差项对回差影响的灵敏度Sj表示为：

为了更好地比较不同误差对总回差的影响程度，把针齿中心圆半径误差作为参照项，利用式(24)求得各误差项的灵敏度指数sj，如表2所示。对比数值可知序号4～13，15，16对应的误差因素对整机回差的影响较大。

3 零件公差和摆线轮修形参数的优化

3.1 多目标优化模型的建立

1)确定优化参数。

经过RV减速器主要参数的灵敏度分析后，选取与摆线轮、针轮相关的误差项以及等距和移距修形量为优化参数。同时，RV减速器回差精度要求较高，零件的公差等级均采用较高的加工等级。以RV减速器参数的初始值为下限值，查阅机械设计手册并考虑实际加工条件来确定上限值[6,20]，确定其取值范围，如表4所示。

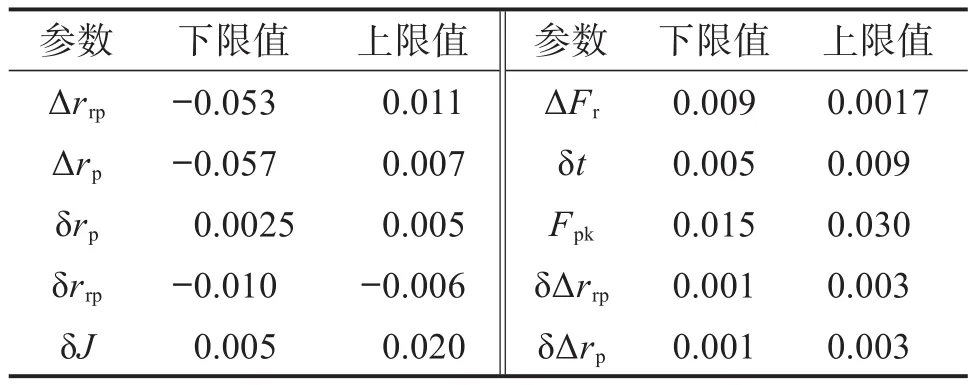
表4 RV减速器优化参数的取值范围Table 4 Value range of optimization parameters of RV reducer 单位：mm

2)建立目标函数。

零件的公差由加工精度决定。公差越小，加工精度越高，对应的制造成本也越高。考虑经济性和实用性，把总制造成本、摆线轮额定寿命内的最大磨损量最小作为优化目标。不同加工特征的成本函数如下[21]。

尺寸公差成本函数C1为：

式中：a1、a2、a3、a4、a5均为成本系数，a1=16.140，a2=0.324，a3=0.217，a4=0.013，a5=2.845；Ei为零件公差。

位置度公差成本函数C2为：

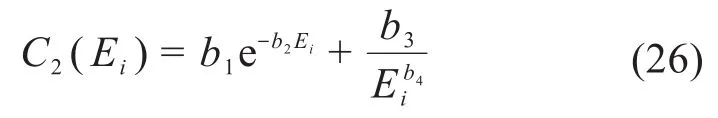
式中：b1、b2、b3、b4均为成本系数，b1=4.862，b2=0.483，b3=0.877，b4=1.020。

跳动公差成本函数C3为：

式中：c1、c2均为成本系数，c1=23.729，c2=0.682。

零件总的公差成本为：

目标函数为：

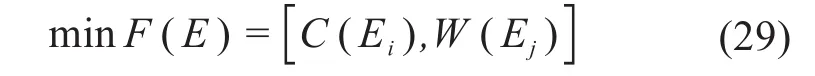
式中：W(Ej)为摆线轮额定寿命内的最大磨损量；Ej为摆线轮的修形参数。

3)设定约束条件。

以传动精度可靠度为约束条件进行优化[22]，要求RV减速器运行6 000 h时的传动精度可靠度不低于预期可靠度Rper，即：

3.2 参数优化设计

分别以RV减速器运行6 000 h时的精度可靠度不低于95%、100%为约束条件1和2，利用遗传算法求解多目标优化问题，得到Pareto前沿解集，如图6所示。Pareto前沿解集中拐点的优化数据较好，加工成本和磨损量都较小，故选取拐点的优化参数作为最优解[23]。对应的优化参数见表5。

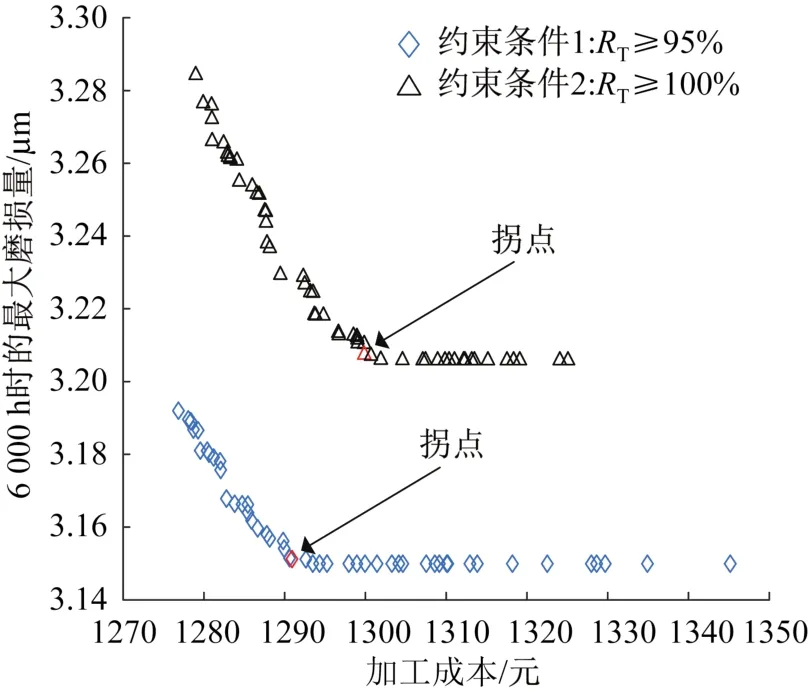
图6 RV减速器多目标优化的Pareto前沿解集Fig.6 Pareto frontal solution set for multi-objective optimization of RV reducer

表5 RV减速器优化后的参数Table 5 Parameters of RV reducer after optimization 单位：mm

可靠度为100%即要求减速器在零件尺寸和磨损量取极限值时的回差仍小于许用值，零件尺寸偏差和修形量应尽可能小，因此，约束条件2下最优解的加工成本高于约束条件1，磨损量也相应地增大。对传动精度可靠度的要求越高，优化后的成本越高。而减速器在整个寿命周期内都存在零件磨损，传动性能会退化，导致精度可靠度下降。在实际工程中应平衡经济性和可靠性，根据应用情况适当调整在预期寿命内的可靠度，通过约束可靠度进行优化设计。

3.3 优化结果分析

由图6可知，在约束条件1和2下，优化后摆线轮运行6 000 h时的最大磨损量分别从3.127 μm增大到 3.151 μm 和 3.207 μm，增加了 0.77% 和 2.56%，总加工成本分别从1 402元下降至1 291元和1 300元，降低了7.92%和7.28%。优化前后RV减速器传动精度可靠度的对比如图7所示。由图可知，优化后减速器传动精度可靠度有明显提高，在额定寿命6 000 h内的可靠度均满足预期要求。

图7 优化前后RV减速器传动精度可靠度对比Fig.7 Comparison of transmission accuracy reliability of RV reducer before and after optimization

4 结论

在计算摆线轮轮齿磨损量的基础上，建立了考虑磨损的RV减速器传动精度可靠度模型，并以动态可靠度为约束条件对减速器的设计参数进行了优化，得到如下结论：

1)通过摆线针轮传动机构的啮合分析和Archard磨损模型计算了摆线轮齿廓的磨损深度，发现齿廓上的磨损分布是不均匀的，磨损深度在齿廓方向呈现先增大后减小的规律。

2)经过仿真数据训练的高斯回归模型能有效预测摆线轮轮齿的磨损量，并且能降低磨损仿真的运算时间，提高磨损预测精度。

3)尽管参数优化前摆线轮在累积转动6 000 h后的磨损量不大，但其传动精度可靠度已经不能满足工作需求，可见磨损对整机回差的影响较大。因此，对RV减速器的传动性能进行优化时不能忽视零件动态磨损的影响。