牵引式下肢康复机器人机构参数优化及轨迹规划
张鹏程,牛建业,刘承磊,宋井科,王立鹏,张建军
(1.河北工业大学机械工程学院,天津 300401;2.河北省机器人感知与人机融合重点实验室,天津 300401;3.燕山大学河北省并联机器人与机电系统重点实验室,河北秦皇岛 066004)
目前,我国人口老龄化的发展趋势不容乐观,预计老年人口数量在2035年将突破3亿,2053年将达到峰值4.87亿,占届时全球老年人口的1/4[1]。随着人口老龄化的加剧,因机体老化、脑卒中等原因造成下肢运动功能障碍或残疾的患者日益增多。因此,研究下肢康复机器人对实现患者下肢运动功能恢复以及解决我国“患者多、康复医师少”的社会问题具有重要意义。
国内外学者在康复机器人研究领域取得了丰硕的成果。瑞士Hocoma医疗器械公司与苏黎世Balgrist医学院联合研制了Lokomat步行康复训练机器人[2],它可以辅助患者模拟健康人的行走状态。饶玲军等[3]设计的外骨骼康复机器人包括外骨骼本体和1副可实现身体重心控制和平衡的拐杖,其能使患者实现站立与行走。Aggogeri等[4]研发的六自由度并联步态训练康复机器人Rutgers Ankle通过调节2个踏板的相对位置与姿态来协助患者进行平地行走、转弯行走以及平衡能力康复训练。Cudby等[5]研制的可穿戴式下肢康复机器人REX可以帮助患者外出行走。Chen等[6]研制了一款名为CUHK-EXO的下肢外骨骼康复机器人,它可以协助患者站立、坐下和行走等。上述穿戴式下肢康复机器人主要服务于康复后期的患者,能够辅助他们恢复行走能力,而对处于康复初期的患者存在一定局限性。
针对上述问题,部分学者提出了末端牵引式下肢康复机器人,其在辅助处于康复初期的患者恢复运动功能方面具有较大潜力。例如:Bouri等[7]研制的牵引式下肢康复机器人Lambda采用左右对称的并联机械结构,能够以水平或垂直的姿态布置,适用于辅助康复初期患者进行矢状面内的康复训练;Monaco等[8]研制的NEUROBike由2个相互垂直安装的导轨和踝部的转动装置组成,能够辅助卧床的患者模拟健康人的行走动作。相较于穿戴式下肢康复机器人,末端牵引式下肢康复机器人还具有轻量化与小型化的特点,且机械结构简单,易于控制,在训练过程中能够保证患者的安全性与舒适性。然而,上述学者研制的末端牵引式下肢康复机器人的训练方式较为单一,并不十分完善。
为满足患者在不同康复时期的训练需求,针对现有下肢康复机器人训练方式单一的问题,从人体下肢运动机理出发,基于仿生学提出一种可实现卧姿、坐姿训练模式的末端牵引式下肢康复机器人,其兼具并联机构和串联机构的优势:结构简单、承载能力强、正解简单、运动灵活和易于控制等。此外,相对于穿戴式下肢康复机器人,所设计的机器人可克服因重力作用下机器人零部件与人体发生相对滑动而导致的人机运动不一致的缺点,进而降低对穿戴性和舒适性的要求。然后,通过对机器人的运动学正、逆解进行分析,并以其安全工作空间为目标函数,通过遗传算法对其机构参数进行优化。接着,根据康复护理相关理论对机器人的康复训练轨迹进行规划。最后,搭建实验平台并开展运动捕捉实验,以验证理论分析的正确性。
1 牵引式下肢康复机器人机构设计及自由度计算
1.1 人体下肢运动机理分析
下肢是人体结构的重要组成部分,其由骨骼、关节、肌肉以及韧带组成,主要起支撑人体重量和辅助人体行走的作用。对人体下肢运动机理进行分析,可为机器人机构设计提供理论基础。
根据人体解剖学原理,利用假想的3个相互垂直的平面将人体分为8个部分。鉴于拟设计的牵引式下肢康复机器人仅针对患者的髋、膝关节进行康复训练,故根据基本切面和基本轴线对人体下肢髋、膝关节的运动进行描述。
髋关节是典型的杵臼关节,从形态上看其近似为球窝关节,其运动形式为矢状面内的屈伸运动、水平面内的内外旋运动以及冠状面内的外展内收运动。膝关节属于滑车关节,其运动形式为矢状面内的屈伸运动。
根据上述分析,在构建人体下肢运动等效模型时,可将髋关节等效为虎克铰链,将膝关节等效为回转副,将足部视作下肢末端。
1.2 机器人机构设计
基于人体下肢运动等效模型,对末端牵引式下肢康复机器人的机构进行设计。由生物学理论可知,人体下肢运动是靠骨骼肌的收缩与舒张实现的,骨骼肌长度的改变可实现相邻2个骨骼的相对转动。故根据仿生学原理,在虎克铰链处布置2条UPS支链来模拟人体大腿的骨骼肌肉,在大腿与小腿之间加入1条RPR支链来模拟人体小腿的肌肉[9],且加入UPS支链和RPR支链可以提高机器人的承载能力,上述支链均以移动副作为驱动副,则以上部分组成(2-UPS&U)+(R&RPR)机构。然后,在(2-UPS&U)+(R&RPR)机构末端加入2条RR支链,通过伺服电机驱动齿轮箱内齿轮的传动实现左、右脚踏板的镜像开合,以辅助患者进行髋关节内外旋的康复训练;脚踏板跟随人体足部运动,不设置驱动。最终组成(2-UPS&U)+(R&RPR)+RR混联机构,如图1(a)所示,对应的机器人三维模型如图1(b)所示。
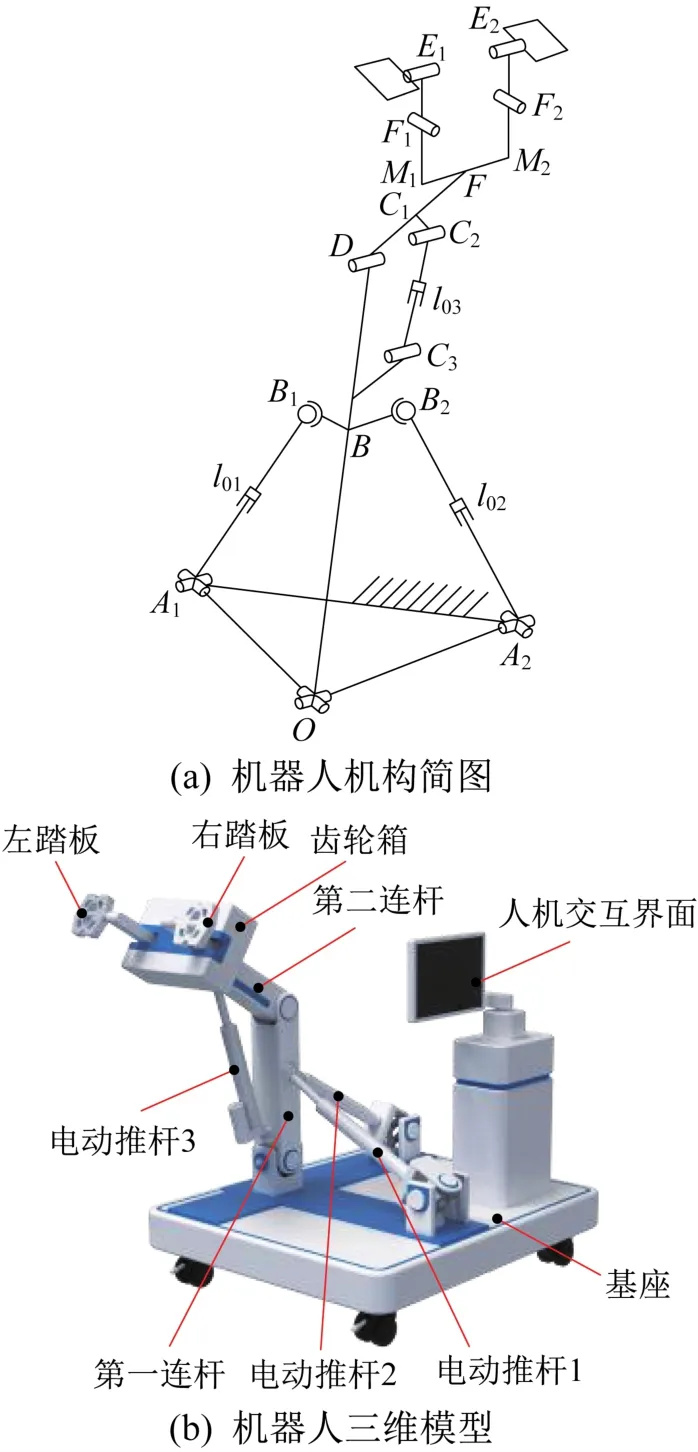
图1 牵引式下肢康复机器人机构简图及三维模型Fig.1 Mechanism sketch and three-dimensional model of traction lower limb rehabilitation robot
1.3 机器人机构自由度计算
利用修正的G-K公式计算(2-UPS&U)+(R&RPR)机构的自由度,计算式如下:

式中:M为机构的自由度;d为机构的阶数;n为机构中构件的数量;g为机构中运动副的数量;fi为第i个运动副的自由度;ν为机构的冗余约束数;η为机构的局部自由度。
由于所设计的机器人并联部分中的UPS支链的自由度为6,不会对OD杆产生约束,故该支链为无约束支链;RPR支链始终与OD杆、DF杆处于同一平面,故该支链产生的约束为冗余约束。由此可知,(2-UPS&U)+(R&RPR)机构的阶数d=6,构件数n=9,运动副数g=11,所有运动副自由度的代数和为20,冗余约束数ν=1,且该机构不存在局部自由度,故η=0。将上述参数代入式(1)即可求得该机构的自由度:

此外,2条RR支链的运动具有一致性,故这2条支链整体的自由度为2。综上,所设计的牵引式下肢康复机器人机构的自由度为5。
2 牵引式下肢康复机器人运动学分析
为计算所设计牵引式下肢康复机器人的运动学正、逆解,构建如图2所示的机构坐标系。其中:固定坐标系O-XYZ的原点为虎克铰链的2条转动轴线的交点,X轴与U支链中虎克铰链的第一转动轴线重合,沿OA2方向;Y轴与U支链中虎克铰链的第二转动轴线重合,沿OA1方向;Z轴由右手定则确定。动坐标系B-XBYBZB的原点位于OD杆上某固定位置处,XB轴沿BB2方向,YB轴沿BB1方向,ZB由右手定则确定。动坐标系D-XDYDZD的XD轴与其原点D处的回转副轴线平行,ZD轴沿OD方向。动坐标系F-XFYFZF的XF轴沿FM2方向,ZF轴沿DF方向。动坐标系F1-XF1YF1ZF1的XF1轴垂直于原点F1处的回转副轴线,YF1轴与原点F1处的回转副轴线平行。动坐标系E1-XE1YE1ZE1的XE1轴垂直于原点E1处的回转副轴线,YE1轴与原点E1处的回转副轴线平行。动坐标系F2-XF2YF2ZF2与E2-XE2YE2ZE2同理,不再赘述。
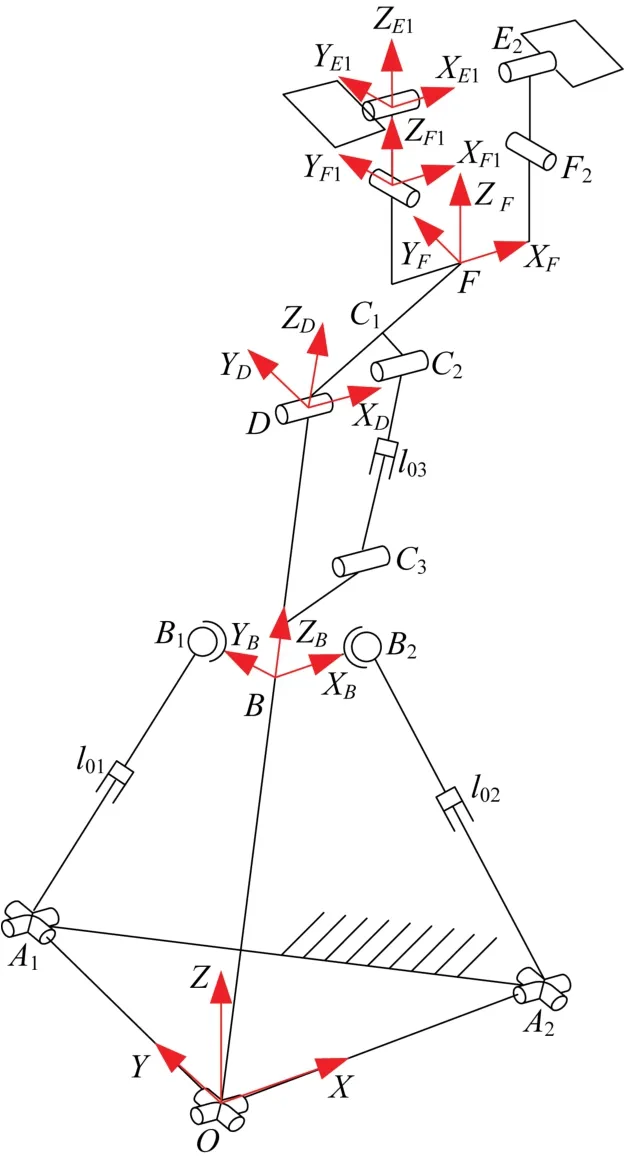
图2 牵引式下肢康复机器人机构运动学坐标系Fig.2 Kinematics coordinate system of traction lower limb rehabilitation robot mechanism
2.1 运动学正解
运动学正解是指在已知各个关节输入参数的情况下求解的末端执行器位置参数。为表述方便,定义OD杆的长度为l1,DF杆的长度为l2,FM1杆、FM2杆的长度为l3,M1F1杆、M2F2杆的长度为l4,F1E1杆、F2E2杆的长度为l5。首先,分析左踏板连接处E1点相对于固定坐标系原点O的位置。动坐标系D-XDYDZD相对于固定坐标系O-XYZ的位姿可看作先绕X轴旋转α,然后绕Y轴旋转β,最后沿OD杆方向平移l1得到。动坐标系F-XFYFZF相对于动坐标系D-XDYDZD的位姿可看作先绕XD轴旋转γ,再沿DF方向平移l2得到。动坐标系F1-XF1YF1ZF1可由动坐标系F-XFYFZF平移得到。动坐标系E1-XE1YE1ZE1相对于动坐标系F1-XF1YF1ZF1的位姿可看作先绕YF1轴旋转-θ,再沿ZF1轴平移l5得到。由此可得,动坐标系E1-XE1YE1ZE1相对于固定坐标系O-XYZ的齐次变换矩阵为:

其中:
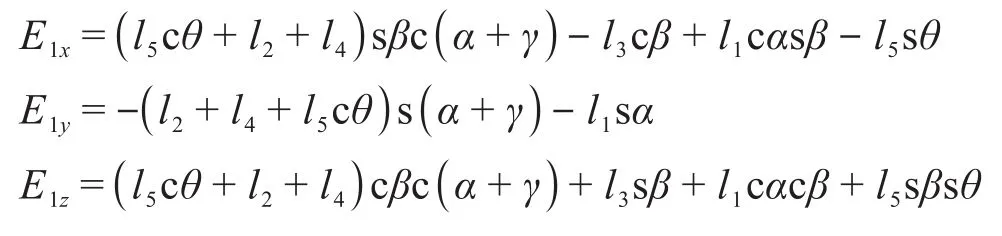
式中:T为各坐标系之间的变换矩阵;c表示cos,s表示sin,下文矩阵中同。
同理可得,动坐标系E2-XE2YE2ZE2相对于固定坐标系O-XYZ的齐次变换矩阵为:
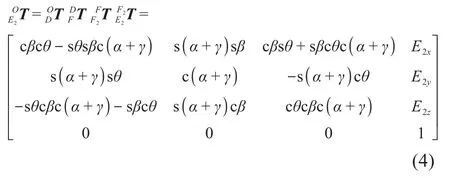
其中:
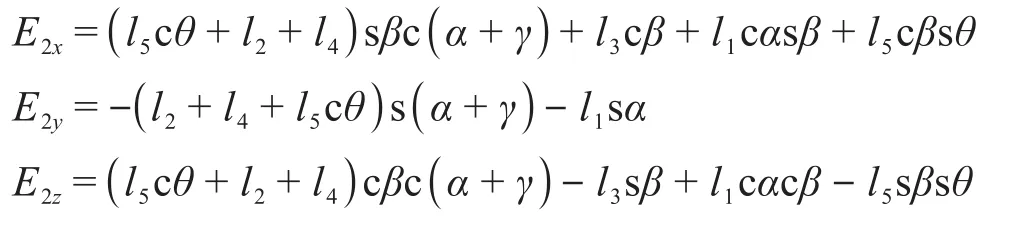
当并联部分(2-UPS&U)的静、动坐标系重合时,动平台B点相对于静平台OA1A2的转动可看作动坐标系B-XBYBZB绕固定坐标系O-XYZ的X轴、Y轴转动,则其旋转矩阵为:

A1、A2、O点在固定坐标系O-XYZ中的位置矢量m1、m2、m3分别为:

式中:a1、a2为静平台的结构参数。
B1、B2、B点在动坐标系B-XBYBZB中的位置矢量n1、n2、n3分别为:
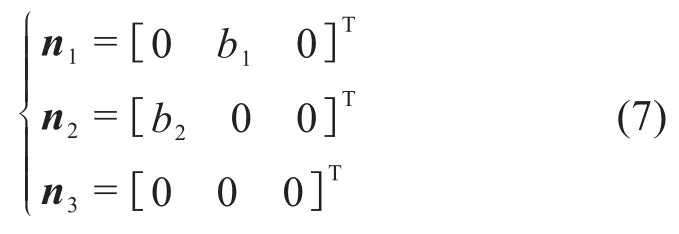
式中:b1、b2为动平台的结构参数。
在固定坐标系O-XYZ下,建立并联部分的位置约束方程:
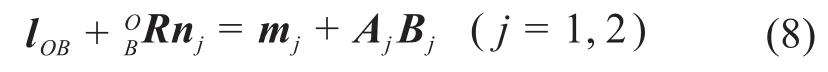
其中:

式中:lOB为OB杆的长度;Aj、Bj分别为Aj、Bj点在固定坐标系O-XYZ中的位置矢量。
代入具体数值并化简,可得电动推杆1,2的长度l01、l02:

在△C2DC3中,根据余弦定理可得:
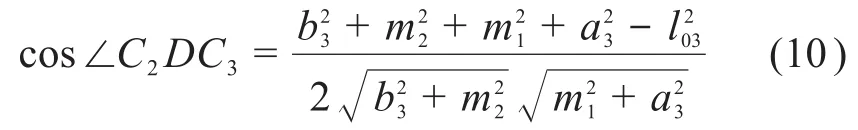
式中:l03为电动推杆3的长度;a3为CC3杆的长度;b3为C1C2杆的长度,m1为CD杆的长度,m2为C1D杆的长度。
由此可得γ的表达式:
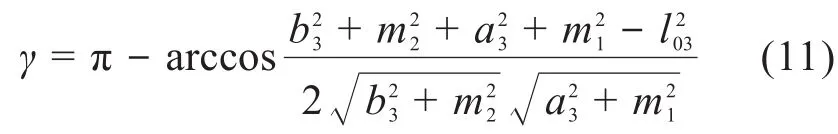
故l03可表示为:

其中:

2.2 运动学逆解
通过变换将动坐标系E1-XE1YE1ZE1与E2-XE2YE2ZE2转换为F-XFYFZF,得到F点在固定坐标系O-XYZ中的位置(Fx,Fy,Fz),从而计算得到α、β与γ:

其中:

将求得的3个转角的值代入式(9)和式(12),可得到3个电动推杆的长度。
3 牵引式下肢康复机器人机构参数优化
为了使所设计的牵引式下肢康复机器人可以更好地满足患者的康复训练需求,以及使患者在训练过程中更加舒适,对其机构参数进行优化。由于康复初期人体关节的活动度较小[10],故以康复中后期坐姿训练状态下人体下肢末端与机器人末端工作空间重合度(即机器人的安全工作空间[11])为目标函数,以机器人机构参数为设计变量,利用MATLAB遗传算法工具箱[12]进行优化计算。
由于该机器人机构中的2条RR支链左右对称,故以人体左下肢与机器人左踏板为对象进行分析。
3.1 人体左下肢运动学分析
将机器人与坐姿状态下的人体下肢看作人机系统,以机器人固定坐标系O-XYZ为人机系统的固定坐标系。根据人体下肢运动等效模型,建立如图3所示的人机系统坐标系。其中:O1-XO1YO1ZO1表示髋关节坐标系,N-XNYNZN表示膝关节坐标系,M-XMYMZM表示足底坐标系;O1表示人体髋关节,N表示人体膝关节,O1N表示人体大腿,其长度为l6;NM表示人体小腿与足部,其长度为l7。

图3 人机系统坐标系Fig.3 Human-machine system coordinate system
令xO1表示人体髋部的横向宽度,yO1表示髋关节在固定坐标系中的Y向位置,zO1表示坐姿状态下人体髋关节距离地面的高度。则动坐标系O1-XO1YO1ZO1的原点O1相对于固定坐标系O-XYZ的原点O的位置为(-xO1,-yO1,zO1)。
动坐标系N-XNYNZN相对于动坐标系O1-XO1YO1ZO1的位姿可看作先绕XO1轴旋转θ1,再绕ZO1轴旋转θ2,最后沿O1N方向平移l6得到。动坐标系M-XMYMZM相对于动坐标系N-XNYNZN的位姿可看作先绕XN轴旋转-θ3,再沿NM方向平移l7得到。故动坐标系M-XMYMZM相对于人机系统固定坐标系的齐次变换矩阵为:

其中:

参考《中国成年人人体尺寸》[13],以身高为1 754 mm、体重为75 kg的男性模型为参考,其对应的下肢参数如下:大腿长度为496 mm、小腿长度为396 mm,足部厚度为75 mm,胯部宽度为335 mm。故取xO1=167.5 mm,zO1=440 mm,l6=496 mm,l7=471 mm。根据人机工程学选取yO1=1 420 mm。规定坐姿状态下人体下肢各关节的康复训练角度,如表1所示。

表1 人体髋膝关节康复训练角度Table 1 Rehabilitation training angle of human hip and knee joints
故可得3个旋转角度θ1、θ2、θ3的取值范围:

将上述参数值代入式(14),可得人体左下肢末端在人机系统固定坐标系中的位置。
令Mx、My、Mz与E1x、E1y、E1z分别对应相等,求得人体左下肢的运动学逆解:

其中:
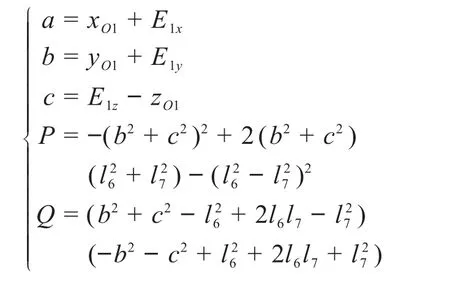
当机器人的输入已知时,可通过式(16)求得人体下肢髋、膝关节的角度。
3.2 设计变量选取
根据左踏板连接处的运动学正解,以机器人机构的主要杆长作为设计变量,即:
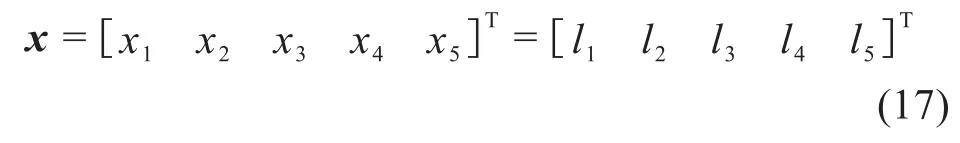
3.3 目标函数确定
机器人末端与人体下肢末端工作空间的重合度越高,表明康复训练效果越好。故以机器人末端与人体下肢末端工作空间对应散点的距离之和最小为目标,建立目标函数S:

式中:Xr、Yr、Zr和xr、yr、zr分别为机器人末端和人体下肢末端在固定坐标系O-XYZ中的坐标;k为工作空间的散点数量。
3.4 约束条件
机构参数的变化会引起机器人工作空间的变化。首先,研究虎克铰链以及回转副的转角范围对机器人工作空间的影响,以“点集数”作为工作空间的评价指标[14]:点集数越大,工作空间越大。
按照固定步长依次改变4个转角的范围,其他参数值全部采用初选值,然后通过单一变量法来研究各转角范围对机器人工作空间的影响。最终得到机器人工作空间随各转角范围的变化曲线,如图4所示。

图4 各转角范围对机器人工作空间的影响Fig.4 Influence of each angle range on robot workspace
由图4可知,虎克铰链与回转副的转角范围越大,机器人的工作空间越大。另外,根据人机工程学考虑训练过程中患者的安全性以及电动推杆的技术要求,最终规定虎克铰链及回转副的转角范围为:

根据人机工程学,确定各设计变量的范围为:

优化后的机器人机构参数如表2所示。

表2 优化后的机器人机构参数Table 2 Optimized robot mechanism parameters单位:mm
采用蒙特卡洛法[15]求解优化后的人机系统工作空间,结果如图5所示。其中:红色部分代表人体左下肢末端的工作空间,蓝色部分代表机器人左踏板的工作空间,两者相交的部分为机器人的安全工作空间。由此可得,矢状面内机器人的安全工作空间区域如图6所示。
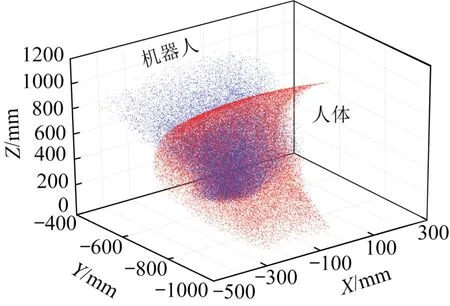
图5 人机系统工作空间Fig.5 Human-machine system workspace

图6 人机系统矢状面工作空间区域Fig.6 Sagittal workspace area of human-machine system
由于下肢康复机器人以辅助患者进行矢状面内的康复训练为主[16],利用式(21)求解人体下肢矢状面内的有效工作空间比ξ[17]:

式中:St为机器人安全工作空间区域;Sw为人体下肢等效模型的工作空间区域。
根据图6和式(21),求得ξ=0.71,说明优化结果良好。此外,由于本文所研究的机器人为末端牵引式下肢康复机器人,其安全工作空间无法与人体下肢等效模型的工作空间完全一致,而根据康复护理相关理论[18],在图6所示的人体末端与机器人末端工作空间的重合区域内,机器人可以帮助人体下肢进行多种康复训练,即机器人对人体有较好的适应性,可以满足其康复需求。
4 牵引式下肢康复机器人轨迹规划
在康复训练的过程中,要求机器人尽量作速度、加速度连续平滑的无冲击运动。五次多项式插值能够解决三次多项式插值的速度变化不平滑且加速度存在突变的问题,故本文采用五次多项式插值法对所设计的牵引式下肢康复机器人进行轨迹规划。
4.1 卧姿康复训练模式轨迹规划
患者在康复初期身体虚弱,无法支撑其体重,处于这个时期的患者适合卧姿康复训练,通过保持正常的关节活动来恢复患者肢体的运动能力,以避免关节变形和肌肉萎缩。根据康复护理相关理论,采用CPM(continous passive motion,持续被动运动)方法[18]进行康复训练。在康复训练过程中,小腿始终保持水平,髋关节与膝关节的角度变化一致。
为了确保运动的灵活性和舒适性,通常要求髋关节与膝关节的初始夹角为10°[18],规定人体髋、膝关节的运动角度为10°~50°,运动起始与终止处的速度与加速度均为0,故髋关节角度的五次插值多项式为:

则可得在人机系统固定坐标系中,人体下肢末端Y、Z方向的位移为:
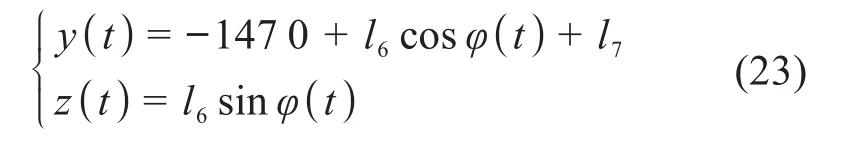
4.2 坐姿康复训练模式轨迹规划
4.2.1 圆周运动训练轨迹规划
当患者处于康复中后期时,适合坐姿康复训练模式。圆周运动训练即人体矢状面内的康复训练,与脚踏车运动类似,能够帮助患者的髋、膝关节进行屈伸运动[19]。以工作空间中某一圆周轨迹为例,其圆心相对人机系统固定坐标系原点的位置(x0,y0,z0)=(-90,-665,470)mm,半径R=115 mm,规定运动时间为10 s。令圆周运动的起始角度为360°,终止角度为0°,起始、终止处的速度与加速度均为0,由此得到圆心角位移的五次插值多项式:
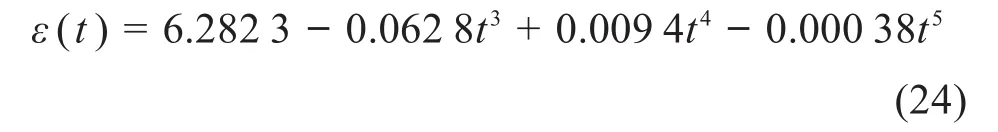
同理可得,在人机系统固定坐标系中,人体下肢末端Y、Z方向的位移为:
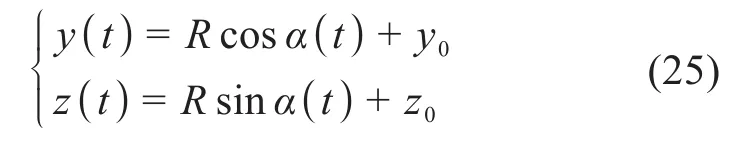
4.2.2 螺旋运动训练轨迹规划
螺旋运动由直线运动与圆周运动组合形成,相较于圆周运动,其可以帮助患者实现空间内的康复训练[20]。定义在人机系统固定坐标系中,圆周分运动的圆心坐标为(x0,y0,z0)=(-200,-630,600)mm,半径R=70 mm;令圆周分运动的起始角度为720°,终止角度为0°。直线分运动的起始位置为(-200,-630,600)mm,终止位置为(0,-630,600)mm;2个分运动的起始与终止处的速度、加速度均为0。规定螺旋运动时间为15 s。由此可得,螺旋运动的2个分运动的五次插值多项式为:

同理可得,在人机系统固定坐标系中,人体下肢末端X、Y、Z方向的位移为:

根据式(9)、式(12)、式(13)可得上述康复训练轨迹下电动推杆长度的变化情况。再根据式(16)可进一步计算出上述康复训练轨迹下人体髋、膝关节运动角度的理论变化值。
5 牵引式下肢康复机器人训练实验
为了验证牵引式下肢康复机器人设计与优化的合理性以及轨迹规划的正确性,根据轨迹规划结果对其电动推杆进行控制,并通过Xsens MVN系统采集康复训练过程中人体髋、膝关节的运动角度数据。由于目前机器人样机的底部没有设置升降装置,故现阶段开展卧姿康复训练实验时,被试者平躺在地面上,以模拟卧床期的患者。
机器人样机选用带上下限位开关的伺服电动推杆作为驱动,采用Copley公司的Accelnet伺服电机驱动器模块驱动电动推杆,选用基于STM32H750的主控板作为主驱动器,通过所搭建的伺服电机驱动系统来实现电动推杆位移的精密控制。考虑到安全性问题,在实验开始前将被试者的足部与机器人样机的脚踏板绑在一起,从而避免两者脱离。
图7和图8所示分别为被试者在卧姿和坐姿状态下进行康复训练的实验现场。

图7 卧姿康复训练实验现场Fig.7 Experimental site of rehabilitation training with lying posture

图8 坐姿康复训练实验现场Fig.8 Experimental site of rehabilitation training with sitting posture
3种康复训练轨迹下人体髋、膝关节运动角度的测量值与理论值对比分别如图9至图11所示。

图9 CPM训练轨迹下人体髋、膝关节运动角度对比Fig.9 Comparison of motion angles of human hip and knee joints under CPM training trajectory
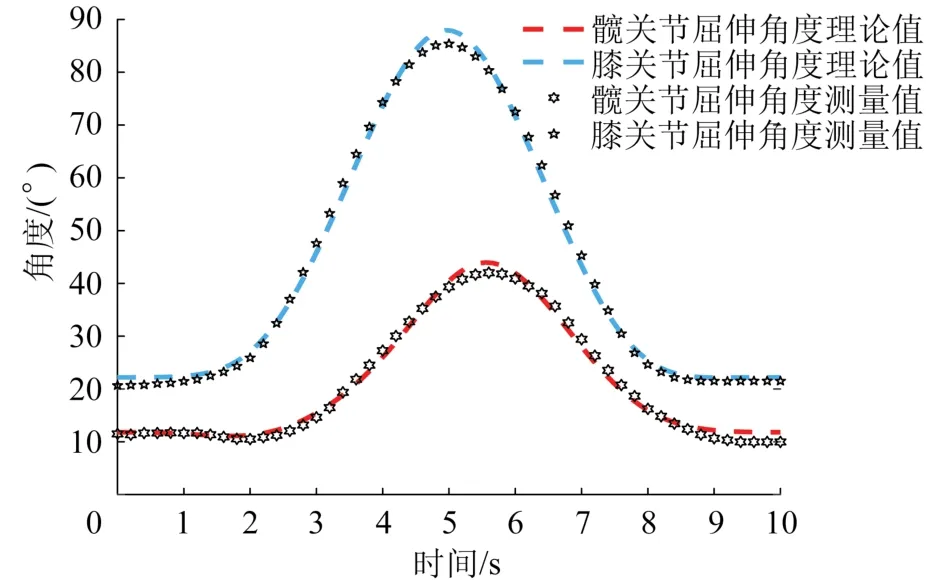
图10 圆周运动训练轨迹下人体髋、膝关节运动角度对比Fig.10 Comparison of motion angles of human hip and knee joints under circular exercise training trajectory

图11 螺旋运动训练轨迹下人体髋、膝关节运动角度对比Fig.11 Comparison of motion angles of human hip and knee joints under spiral training trajectory
从图9至图11中可知,髋、膝关节运动角度的理论值与测量值基本一致;在3种训练轨迹下,髋关节运动角度的最大误差约为2.8°,膝关节运动角度的最大误差约为4.2°。产生误差的原因是在实验过程中被试者的腿部会不自主地抖动,且被试者与标准人体尺寸存在差异。另外,被试者的足底与机器人脚踏板之间可能会发生微小的相对移动,也会导致实验结果产生偏差。但总体来说,误差在许用范围之内,且人体髋、膝关节的活动度符合人体康复运动参数,验证了机器人的设计及其优化后的安全工作空间的合理性以及轨迹规划的正确性。
6 结论
1)为满足下肢运动功能障碍患者在不同阶段的康复训练需求,针对现有下肢康复机器人训练方式单一的问题,根据人体下肢运动机理以及仿生学,设计了一种可实现卧姿、坐姿训练模式的牵引式下肢康复机器人。
2)基于对牵引式下肢康复机器人的运动学分析,将人体下肢末端与机器人末端工作空间的重合部分作为机器人的安全工作空间,并以此为目标函数,通过遗传算法对机器人的机构参数进行了优化;同时,根据优化结果绘制人机系统工作空间散点图,得到矢状面内人体下肢的有效工作空间比为0.71,表明优化结果良好。
3)根据康复护理相关理论,在机器人安全工作空间内分别开展卧姿、坐姿康复训练轨迹规划,并通过实验对理论分析结果进行了验证。结果表明,机器人设计与参数优化合理以及轨迹规划正确,可为人机交互系统的研究奠定基础。
4)本文仅针对被动训练进行了研究,后续将通过在人体与机器人的接触部位安装力/力矩传感器来获取人机之间的交互力,以进行人体运动意图识别,并在此基础上制定控制策略,以实现机器人助力训练以及主动训练。此外,还将通过理论分析与实验建立患者舒适度与康复效果的评价指标体系,以使机器人能够更好地辅助患者进行康复训练。

